基于插板法膜压力模型的沥青混合料水稳定性评价

引用本文

罗蓉, 曾哲, 张德润, 冯光乐, 董华均. 基于插板法膜压力模型的沥青混合料水稳定性评价[J].吉林大学学报（工学版）, 2017,47(6): 1753-1759
LUO Rong, ZENG Zhe, ZHANG De-run, FENG Guang-le, DONG Hua-jun. Moisture stability evaluation of asphalt mixture based on film pressure model of Wilhelmy plate method[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1753-1759 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706011
Permissions

基于插板法膜压力模型的沥青混合料水稳定性评价

罗蓉^1,², 曾哲^1,², 张德润^1,², 冯光乐³, 董华均⁴

1.武汉理工大学交通学院,武汉 430063

2.湖北省公路工程技术研究中心,武汉 430063

3.湖北省交通厅工程质量监督局,武汉430014

4.湖北长江路桥股份有限公司,武汉 430212

作者简介:罗蓉(1979-),女,教授,博士生导师.研究方向:道路沥青混合料损伤机理.E-mail:rongluo@whut.edu.cn

基金:交通运输部建设科技项目(2014318J22120)

摘要

为了揭示传统插板法计算模型中未考虑后退过程中沥青表面液体膜压力的影响以及存在沥青表面能无解这两个缺陷,本文以添加抗剥落剂后的沥青和酸性砾石集料为样品进行插板法试验,分别采用传统模型和基于膜压力的模型计算沥青表面能,并分析了沥青混合料的水稳定性指标ER₁和ER₂,然后按照ASTM D3625规范进行水煮法试验。结果表明:基于膜压力的模型能够弥补传统插板法模型的两个缺陷,且通过该方法计算得到的沥青混合料水稳定性指标排序与水煮法试验得到的排序结果一致。

关键词: 道路工程; 沥青混合料; 插板法; 表面能; 膜压力; 水稳定性

中图分类号:U414 文献标志码:A 文章编号:1671-5497(2017)06-1753-07

Moisture stability evaluation of asphalt mixture based on film pressure model of Wilhelmy plate method

LUO Rong^1,², ZENG Zhe^1,², ZHANG De-run^1,², FENG Guang-le³, DONG Hua-jun⁴

1.School of Transportation, Wuhan University of Technology, Wuhan 430063, China

2.Center for Advanced Technology of Road Engineering in Hubei, Wuhan 430063, China

3.Engineering Quality Supervision Bureau, Transportation Department of Hubei Province, Wuhan 430014, China

4.Hubei Chang Jiang Road and Bridge Co., Ltd., Wuhan 430212, China

Abstract

The traditional calculation model of Wilhelmy plate method has two deficiencies: the effect of liquid film pressure on the surface of asphalt binders during the receding process is out of consideration and the surface energy components are sometimes unsolvable. To overcome these two deficiencies, taking the asphalt binders, in which anti-stripping agents were added, and acidic gravel as the test samples, the traditional model and the model based on film pressure were used to calculate the surface energy of the asphalt binders, respectively. The moisture stability indexes ER1 and ER2 of the asphalt mixtures were analyzed. In addition, the moisture stability performances of the test samples were assessed using the water-boiling test following the guidelines of ASTM D3625. The comparative results show that the film pressure calculation model is able to eliminate the two deficiencies, and the moisture stability performance ranking of the asphalt mixtures predicted by the model agrees well with that determined by the water-boiling tests.

Keyword: road engineering; asphalt mixture; wilhelmy plate method; surface energy; film pressure; moisture stability

Show Figures

0 引言

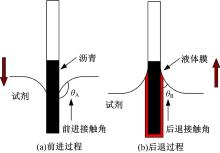
插板法因试验操作简便、快捷, 目前被广泛用于沥青材料表面能测试。其基本原理为^{[1, 2, 3]}:通过沥青膜浸入及撤出试剂形成前进和后退动态接触角, 利用vOGC(van Oss-Good-Chaudhury)三参数模型联立方程组求解得到对应前进和后退过程的两套表面能参数, 再分别使用这两套参数评价沥青混合料的愈合和抗开裂性能。然而该测试模型仍然存在以下两方面的不足:①后退过程测试的接触角及其对应的表面能并不可靠:沥青在撤出试剂时表面会裹覆一层液体膜, 液体膜产生的扩张压力导致沥青表面特性发生改变^[4], 从而造成明显的滞后效应^{[5, 6]}并影响后退接触角的大小。因此, 后退过程不能反映沥青材料与液体试剂的真实接触情况, 若要计算其对应的表面能, 必须考虑沥青表面的液体膜影响; ②传统的vOGC模型认为材料的表面能由3个基本分量构成^[1], 通过分量相互作用建立方程求解表面能。但是该模型已被证实存在分量开根号为负值^{[7, 8]}、试剂表面能分量建立在水的表面能酸碱分量比值为1这一假设基础上^[1]等缺陷, 因此采用该方法计算沥青表面能存在一定的弊端。

本文针对传统插板法模型的不足, 从测试的动态过程入手, 考虑后退过程中沥青被润湿后表面的液体膜压力, 得到对应于材料自身的表面能参数。在此基础上匹配相应的表面能水稳定性评价指标, 与传统的vOGC模型进行对比并通过水煮法试验加以验证, 从而为更准确地测试沥青材料表面能、评价沥青混合料水稳定性提供一定的理论基础。

1 插板法原理和两种计算模型

1.1 插板法原理

使用插板法测试沥青表面能的原理^{[1, 3]}是:将沥青均匀地涂膜到洁净玻片上, 缓慢浸入到测试试剂中再撤出, 根据受力平衡, 由仪器天平受力变化的差值Δ F及玻片浸入深度h计算接触角θ :

$\begin{matrix} cosθ = \frac{ΔF + ab h ρ' g}{2 (a + b) γ_{L}} (1) \end{matrix}$

式中:Δ F为沥青膜浸入测试试剂前、后的受力差值; a、b分别为沥青涂膜玻片的宽度和厚度; h为玻片浸入试剂的深度; ρ '为试剂密度与空气密度的差值; g为重力加速度; γ _L为测试试剂的表面能。

1.2 传统计算模型

在传统vOGC模型中, 认为材料的表面能γ 由非极性色散分量γ ^LW和极性酸碱分量γ ^AB组成, 其中γ ^AB又由极性酸分量γ ⁺和极性碱分量γ ^-组成^{[1, 2]}。

对于插板法得到的接触角, 该模型按照以下步骤计算沥青表面能^[3]:首先联立杨氏方程(式(2))和Dupre公式(式(3)), 得到式(4):

$γ_{S} = γ_{SL} + γ_{L} cosθ (2)$

$γ_{SL} = γ_{S} + γ_{L} - W^{a} (3)$

$W^{a} = γ_{L} (1 + cosθ) (4)$

式中: $\begin{matrix} γ_{S} \end{matrix}$ 为沥青表面能; $\begin{matrix} γ_{SL} \end{matrix}$ 为沥青-试剂间的表面能; θ为接触角; W^a为沥青-试剂间的粘附功。

用表面能分量表示粘附功W^a, 代入式(4)得到Young-Dupre方程:

$\begin{matrix} (1 + cosθ) γ_{L} = 2 (\sqrt[]{γ_{S}^{LW} γ_{L}^{LW}} + \sqrt[]{γ_{S}^{+} γ_{L}^{-}} + \sqrt[]{γ_{S}^{-} γ_{L}^{+}}) (5) \end{matrix}$

式中:参数下标中的S和L分别代表沥青和液体试剂。

由于已知液体试剂的表面能, 接触角 $\begin{matrix} θ \end{matrix}$ 可由插板法测试得到, 故式(5)中未知的参数只有 $\begin{matrix} γ_{S}^{LW} \end{matrix}$ 、 $\begin{matrix} γ_{S}^{+} \end{matrix}$ 和 $\begin{matrix} γ_{S}^{-} \end{matrix}$ 。选定至少3种不同测试试剂, 分别测定它们与沥青的接触角 $\begin{matrix} θ, \end{matrix}$ 便可联立方程组求解沥青的3个表面能分量, 并进一步得到表面能总量γ _S:

$\begin{matrix} γ_{S} = γ_{S}^{LW} + 2 \sqrt[]{γ_{S}^{+} γ_{S}^{-}} (6) \end{matrix}$

插板法既测定了前进接触角θ _A, 又测定了后退接触角θ _R, 故最终代入计算时可用两类接触角分别得到对应前进过程和后退过程的两套表面能参数。

1.3 基于膜压力的计算模型

基于膜压力的计算模型可直接求解表面能总量, 推导过程^[4]为:将前进接触角θ _A代入杨氏方程:

$\begin{matrix} γ_{S} = γ_{SL} + γ_{L} \cos θ_{A} (7) \end{matrix}$

后退过程中, 沥青从液体中撤出时, 液体试剂会浸润在沥青表面形成一层液体膜, 考虑此时的薄膜压力, 杨氏方程相应地变为:

$\begin{matrix} \begin{matrix} γ_{SF} = γ_{SL} + γ_{L} \cos θ_{R} (8) \\ γ_{SF} = γ_{S} + λ (9) \end{matrix} \end{matrix}$

式中:γ _SF为被液体膜裹覆后沥青的表面能; $\begin{matrix} λ \end{matrix}$ 为薄膜压力(如果液体没有完全润湿固体, 则 $\begin{matrix} λ \end{matrix}$ 为正; 反之 $\begin{matrix} λ \end{matrix}$ 为负)。

联立式(7)~(9), 得:

$\begin{matrix} λ = γ_{L} (\cos θ_{R} - \cos θ_{A}) (10) \end{matrix}$

	Figure Option View Download New Window
	图1 前进和后退过程中的接触角Fig.1 Advancing angle and receding angle

将前进、后退过程中的参数分别代入式(4), 再相减得到:

$\begin{matrix} W_{R}^{a} - W_{A}^{a} = γ_{L} (\cos θ_{R} - \cos θ_{A}) = λ (11) \end{matrix}$

式中: $\begin{matrix} W_{A}^{a} \end{matrix}$ 和 $\begin{matrix} W_{R}^{a} \end{matrix}$ 分别表示前进和后退过程中的粘附功。

使用Good参数 $\begin{matrix} φ \end{matrix}$ 可以表示物质间的粘附功^[9], 如式(12)所示:

$\begin{matrix} W^{a} = 2 φ \sqrt[]{γ_{1} γ_{2}} (12) \end{matrix}$

式中: $\begin{matrix} γ_{1} \end{matrix}$ 和 $\begin{matrix} γ_{2} \end{matrix}$ 分别表示两种不同物质各自的表面能参数。

将前进、后退过程中沥青和试剂的表面能代入式(12), 同时将粘附功比值表示为k, 如式(13)所示:

$\begin{matrix} \frac{W_{A}^{a}}{W_{R}^{a}} = \frac{2 φ \sqrt[]{γ_{S} γ_{L}}}{2 φ \sqrt[]{γ_{SF} γ_{L}}} = k (13) \end{matrix}$

将前进和后退接触角分别代入式(4), 同样可得到粘附功的比值k, 如式(14)所示:

$\begin{matrix} \frac{W_{A}^{a}}{W_{R}^{a}} = \frac{γ_{L} (1 + \cos θ_{A})}{γ_{L} (1 + \cos θ_{R})} = k (14) \end{matrix}$

联立式(9)(13)得到式(15), 再将式(15)中的 $\begin{matrix} λ \end{matrix}$ 和 $\begin{matrix} k \end{matrix}$ 分别用式(10)和式(14)表示, 可得式(16):

$\begin{matrix} \begin{matrix} γ_{S} = \frac{λ k^{2}}{1 - k^{2}} (15) \\ γ_{S} = \frac{γ_{L} (\cos θ_{R} - \cos θ_{A}) (1 + \cos θ_{A})^{2}}{(1 + \cos θ_{R})^{2} - (1 + \cos θ_{A})^{2}} (16) \end{matrix} \end{matrix}$

选用至少一种试剂, 测定其与沥青的接触角, 代入式(16)便可直接计算沥青表面能。

2 基于表面能的沥青混合料水稳定性指标

沥青路面的水损害, 一般是指渗入路面内部结构空隙或微裂缝中的水在真空负压力或孔隙水压力作用下, 逐渐将沥青从集料表面剥离, 进而导致沥青混合料丧失粘结力并被破坏的过程^[10]。该过程可使用无水条件下沥青与集料的粘附功 $\begin{matrix} W_{12}^{a} \end{matrix}$ 和有水条件下沥青与集料的粘附功 $\begin{matrix} W_{132}^{a} \end{matrix}$ 来表征, 两者比值的绝对值定义为水稳定性指标ER₁, 进一步考虑沥青的润湿特性可使用指标ER₂ (包含破坏沥青内聚能所需做的功 $\begin{matrix} W_{11}^{c} \end{matrix}$ )。一般而言, $\begin{matrix} E R_{1} 和 E R_{2} \end{matrix}$ 值越大, 则沥青混合料水稳定性越好^{[2, 3]}。

$E R_{1} = |\frac{{W^{a}}_{12}}{{W^{a}}_{132}}| (17)$

$E R_{2} = |\frac{{W^{a}}_{12} - {W^{c}}_{11}}{{W^{a}}_{132}}| (18)$

2.1 传统计算模型

在传统模型中, 使用表面能的各个分量来表示粘附功^[1]:

${W^{a}}_{12} = 2 (\sqrt[]{γ_{1}^{LW} γ_{2}^{LW}} + \sqrt[]{γ_{1}^{+} γ_{2}^{-}} + \sqrt[]{γ_{1}^{-} γ_{2}^{+}}) (19)$

${W^{c}}_{11} = 2 γ_{1}^{LW} + 4 \sqrt[]{γ_{1}^{+} γ_{1}^{-}} (20)$

$\begin{matrix} \begin{matrix} {W^{a}}_{132} = 2 (γ_{3} + \sqrt[]{γ_{1}^{LW} γ_{2}^{LW}} + \sqrt[]{γ_{1}^{+} γ_{2}^{-}} + \sqrt[]{γ_{2}^{+} γ_{1}^{-}} \\ - \sqrt[]{γ_{1}^{LW} γ_{3}^{LW}} - \sqrt[]{γ_{3}^{LW} γ_{2}^{LW}} - \sqrt[]{γ_{1}^{+} γ_{3}^{-}} \\ - \sqrt[]{γ_{1}^{-} γ_{3}^{+}} - \sqrt[]{γ_{3}^{-} γ_{2}^{+}} - \sqrt[]{γ_{2}^{-} γ_{3}^{+}}) (21) \end{matrix} \end{matrix}$

式中:参数下标中的1、2和3分别代表沥青、集料和水。

2.2 基于膜压力的计算模型

在基于膜压力的计算模型中, 粘附功直接由表面能总量表示, 结合Good提出的粘附功表达式^{[4, 9]}, $\begin{matrix} {W^{a}}_{12} \end{matrix}$ 和 $\begin{matrix} {W^{c}}_{11} \end{matrix}$ 可表达为:

${W^{a}}_{12} = 2 φ \sqrt[]{γ_{1} γ_{2}} (22)$

${W^{c}}_{11} = 2 φ \sqrt[]{γ_{1} γ_{1}} = 2 φ γ_{1} (23)$

将各粘附功代入热力学平衡方程(式(22)), 得到 $\begin{matrix} {W^{a}}_{132} \end{matrix}$ 的表达式:

${W^{a}}_{132} = {W^{a}}_{12} - {W^{a}}_{13} - {W^{a}}_{23} + {W^{c}}_{33} (24)$

${W^{a}}_{132} = 2 φ (\sqrt[]{γ_{1} γ_{2}} - \sqrt[]{γ_{1} γ_{3}} - \sqrt[]{γ_{2} γ_{3}} + γ_{3}) (25)$

式中: $\begin{matrix} {W^{c}}_{33} \end{matrix}$ 表示破坏水自身的内聚能所需做的功。

将相应参数代入 $\begin{matrix} E R_{1} 和 E R_{2} \end{matrix}$ 后, 可根据指标大小对样品的水稳定性进行排序比较。

3 试验材料及方法

3.1 试验材料

试验选用50#与70#基质沥青, 它们的基本性能指标如表1所示, 按0%、0.2%、0.4%和0.6%的4个掺量向沥青中掺配同一种抗剥落剂, 制备成8种待测沥青样品。选用蒸馏水、丙三醇和乙二醇作为表面能测试试剂, 其表面能参数如表2所示^[3]。集料样品选用典型的酸性砾石(SiO₂含量为87.5%), 使用蒸气吸附法测定它的表面能为236.5× 10^-3J/m²。

表1 沥青材料的基本性能指标 Table 1 Basic properties of asphalt binder samples

表2 20 ° C时试剂的表面能参数 Table 2 Surface energies of probe liquids at 20 ° C10^-3 J/m²

3.2 插板法试验

将沥青样品涂膜到玻片上后, 使用游标卡尺测试沥青涂膜玻片的宽、厚度, 然后将沥青涂膜玻片垂直固定在表面张力仪的天平夹具上。在表面张力仪中放置液体试剂, 调整涂膜玻片与液体试剂的相对位置并启动测试, 通过测试沥青膜浸入和撤出试剂的动态过程, 得到受力变化值与玻片浸入深度的关系, 再将所测参数代入式(1)计算得到接触角。

3.3 ASTM D3625水煮法试验

参照ASTM D3625水煮法规程^[11], 将蒸馏水装入洁净的烧杯中加热至微沸状态, 选定13.2~19 mm的酸性砾石, 用蒸馏水洗净, 再将砾石和沥青样品放入烘箱中加热至150 ° C, 一段时间后取出砾石, 趁热与沥青样品拌匀, 并取出250 g沥青混合料放进加热蒸馏水的烧杯中(此时混合料的温度须为85~100 ° C), 浸煮沥青混合料10 min± 15 s, 然后取出它们放在干净的蜡纸上晾干。对于每种沥青样品, 随机挑选10颗沥青混合料, 用高清相机拍摄每颗混合料正反两面的照片, 将照片导入Image Pro-plus图像分析软件, 利用软件计算每颗混合料的剥落面积和总面积并分别求出它们的平均值, 再将总面积减去剥落面积得到残留面积值, 计算残留面积与总面积的比值得到沥青残留率。

如图2所示, 以一颗沥青混合料为例说明在Image Pro-plus图像分析软件中计算面积的过程:图2(a)表示在软件中绘制的混合料总面积范围, 选定量度单位后由软件自动测定面积; 图2(b)表示在软件中绘制的沥青剥落面积, 其数值也由软件自动测定。将每种样品随机选出的10颗混合料分别进行上述计算过程, 可以得到10颗混合料的剥落面积平均值及总面积平均值, 再用总面积减去剥落面积得到残留面积, 进而得到沥青残留率。

	Figure Option View Download New Window
	图2 计算一颗沥青混合料的面积比例Fig.2 Process of calculating retained coating of asphalt mixture

4 结果及讨论

4.1 接触角结果

采用插板法在20 ° C常湿条件下测试沥青样品与测试试剂的接触角, 结果如表3和表4所示。可以看出:对于两种沥青, 前进接触角随着抗剥落剂掺量的增加而减小, 后退接触角随着抗剥落剂掺量的增加而增大。

4.2 两种模型的结果对比

根据传统计算模型, 将接触角代入式(5)求解沥青表面能, 形成三元一次方程组求解未知参数, 结果如表5所示。可以看出:求解参数中除了后退过程中G样品有正解(39.22× 1 $\begin{matrix} {0^{- 3}}^{} \end{matrix}$ J/m²)外, 其他结果都出现开根号为负数的情况, 即该模型无解。

根据基于膜压力的计算模型, 可求得沥青样品的表面能如表6所示。由于3种测试试剂分别测试得到的表面能数值随抗剥落剂掺量增加的变化趋势相同, 为使3组数据都能发挥作用, 将3组接触角都代入式(16), 以公式两侧之差的平方和最小为目标进行规划求解, 仅得到一组表面能值, 如表6所示, 将该组值作为膜压力理论模型的求解值。

对比两种模型发现:前者无解的情况下后者可通过直接求解表面能总量得到相应值, 而前者得到的唯一正解为39.22× 10^-3 J/m², 对于相同样品, 它与后者所得的值(22.74× 10^-3 J/m²)相差较大, 除了求解过程中表面能分量的影响外, 膜压力是造成该结果的主要原因。

表3 前进过程中接触角的测试结果 Table 3 Contact angles in advancing process (° )

表4 后退过程中接触角的测试结果 Table 4 Contact angles in receding process (° )

表5 vOGC三参数模型计算的沥青表面能参数 Table 5 Surface energies calculated by vOGC model

沥青样品	前进过程			后退过程
沥青样品	$\begin{matrix} \sqrt[]{γ_{S}^{LW}} \end{matrix}$	$\begin{matrix} \sqrt[]{γ_{S}^{+}} \end{matrix}$	$\begin{matrix} \sqrt[]{γ_{S}^{-}} \end{matrix}$	$\begin{matrix} \sqrt[]{γ_{S}^{LW}} \end{matrix}$	$\begin{matrix} \sqrt[]{γ_{S}^{+}} \end{matrix}$	$\begin{matrix} \sqrt[]{γ_{S}^{-}} \end{matrix}$
A	10.29	-3.96	0.20	-25.60	24.41	12.12
B	10.12	-3.82	0.42	-21.47	21.27	11.36
C	6.25	-0.84	1.07	-21.02	20.87	11.30
D	10.18	-3.63	0.40	-21.34	21.08	11.25
E	13.93	-6.73	-0.58	-9.93	12.91	6.86
F	13.39	-6.20	-0.55	-2.51	7.36	5.48
G	11.33	-4.69	0.18	2.47	3.60	4.60
H	15.71	-7.84	-0.56	10.12	-2.22	3.30

表5 vOGC三参数模型计算的沥青表面能参数 Table 5 Surface energies calculated by vOGC model

表6 膜压力理论模型计算的沥青表面能 Table 6 Surface energies calculated by film pressure model10^-3J/m²

4.3 水稳定性评价分析

利用酸性砾石和8种沥青样品的表面能, 计算出它们组合的水稳定性指标, 结果如表7所示。可以看出, 对于50#沥青和70#沥青, 随着抗剥落剂掺量的增加, 沥青混合料水稳定性都变得越来越好。按照ER₁和ER₂值对沥青混合料水稳定性按照从大到小排序, 其顺序为:

H、D、G、C、F、B、E、A

表7 沥青样品与砾石组合的ER₁和ER₂值 Table 7 ER₁ and ER₂of combinations between asphalt binders and gravel

说明无论是否掺配抗剥落剂, 相同条件下的70#基质沥青比50#基质沥青与酸性砾石结合的水稳定性更好。

ASTM水煮法试验结果如表8所示, 对于50#沥青和70#沥青, 随着抗剥落剂掺量增加, 样品中沥青残留率的比例逐渐增大, 证明沥青混合料的水稳定性越来越好, 这与ER₁、ER₂的变化规律相吻合。按照沥青残留率对混合料水稳定性按照从大到小排序, 其顺序为:

H、D、G、C、F、B、E、A

表8 水煮法试验结果 Table 8 Results of water-boiling test

可以看出, 排序结果与表面能理论计算的结果基本一致, 验证了基于膜压力计算模型的有效性。但是, 当水煮法得到的沥青残留率在95%以上时, 混合料颗粒的剥落情况从肉眼直观上看已经不太明显, 即使使用Image Pro-plus图像分析软件, 由于剥落面积较小, 软件捕捉的区域也可能存在较小的误差, 因此对混合料进行水稳定性排序时, 用表面能的计算结果来量化评价更准确。

5 结论

(1)基于膜压力的插板法模型考虑了后退过程中沥青表面的薄膜压力, 且该方法不借助分量直接计算表面能总量, 可以避免求解过程中分量无解的情况。

(2)分析沥青混合料的水稳定性指标发现, 无论是50#还是70#基质沥青, 它们与砾石结合的表面能指标ER₁和ER₂都随抗剥落剂掺量的增加而增大, 说明其水稳定性越来越好。

(3)使用ASTM水煮法验证沥青混合料的水稳定性, 计算沥青残留率后发现, 对于两种沥青来说, 随着抗剥落剂的增加, 沥青残留率都会逐渐增大, 说明沥青混合料的水稳定性越来越好, 这与表面能计算结果吻合。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Lytton R L, Masad E A, Zollinger C, et al. Measurements of surface energy and its relationship to moisture damage[J/OL]. [2016-07-19]. http://tti.tamu.edu/documents/0-4524-2.pdf. [本文引用:6]
[2]	Bhasin A. Development of methods to quantify bitumen-aggregate adhesion and loss of adhesion due to water[J/OL]. [2016-07-19]. http://oaktrust.library.tamu.edu/bitstream/handle/1969.1/5934/etd-tamu-2006A-CVEN-Bhasin.pdf. [本文引用:3]
[3]	张德润, 罗蓉, 陈彧, 等. 基于表面自由能的煤直接液化残渣改性沥青性能分析[J]. 中国公路学报, 2016, 29(1): 22-28. Zhang De-run, Luo Rong, Chen Yu, et al. Performance analysis of DCLR-modified asphalt binders based on surface energy measurements[J]. China Journal of Highway and Transport, 2016, 29(1): 22-28. [本文引用:5]
[4]	Chibowski E, Ontiveros-Ortega A, Perea-Carpio R. On the interpretation of contact angle hysteresis[J]. Journal of Adhesion Science and Technology, 2002, 16(10): 1367-1404. [本文引用:3]
[5]	Wang J H, Claesson P M, Parker J L, et al. Dynamic contact angles and contact angle hysteresis of plasma polymers[J]. Langmuir, 1994, 10(10): 3887-3897. [本文引用:1]
[6]	Miyama M, Yasuda H K. Surface dynamics of plasma polymers studied by the wilhelmy force measurement[J]. Langmuir, 1998, 14(4): 960-964. [本文引用:1]
[7]	Kwok D Y. The usefulness of the Lifshitz-van der Waals/acid-base approach for surface tension components and interfacial tensions[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 1999, 156(1): 191-200. [本文引用:1]
[8]	Volpe C D, Siboni S, Maniglio D, et al. Recent theoretical and experimental advancements in the application of van Oss-Chaudury-Good acid-base theory to the analysis of polymer surfaces I. General aspects[J]. Journal of Adhesion Science and Technology, 2003, 17(11): 1425-1456. [本文引用:1]
[9]	Good R J. Contact angle, wetting, and adhesion: a critical review[J]. Journal of Adhesion Science & Technology, 1992, 6(12): 1269-1302. [本文引用:2]
[10]	高巍, 郭黎黎, 韩森, 等. SMA路面抗水损害研究[J]. 公路, 2009(6): 50-53. Gao Wei, Guo Li-li, Han Sen, et al. Research on moisture susceptibility of SMA pavement[J]. Highway, 2009(6): 50-53. [本文引用:1]
[11]	ASTM D3625-2012. Stand ard practice for effect of water on bituminous-coated aggregate using boiling water[S]. [本文引用:1]

0.0

... 其基本原理为^[1,2,3]:通过沥青膜浸入及撤出试剂形成前进和后退动态接触角,利用vOGC(van Oss-Good-Chaudhury)三参数模型联立方程组求解得到对应前进和后退过程的两套表面能参数,再分别使用这两套参数评价沥青混合料的愈合和抗开裂性能 ...

... ②传统的vOGC模型认为材料的表面能由3个基本分量构成^[1],通过分量相互作用建立方程求解表面能 ...

... 但是该模型已被证实存在分量开根号为负值^[7,8]、试剂表面能分量建立在水的表面能酸碱分量比值为1这一假设基础上^[1]等缺陷,因此采用该方法计算沥青表面能存在一定的弊端 ...

... 1 插板法原理使用插板法测试沥青表面能的原理^[1,3]是:将沥青均匀地涂膜到洁净玻片上,缓慢浸入到测试试剂中再撤出,根据受力平衡,由仪器天平受力变化的差值#cod#x00394 ...

... ^-组成^[1,2] ...

... 1 传统计算模型在传统模型中,使用表面能的各个分量来表示粘附功^[1]: ...

0.0

... ^-组成^[1,2] ...

... 一般而言, ER1和ER2值越大,则沥青混合料水稳定性越好^[2,3] ...

2016

0.0

. 2016, 29(1):22-28

Performance analysis of DCLR-modified asphalt binders based on surface energy measurements

基于表面自由能的煤直接液化残渣改性沥青性能分析

Zhang De-run , Luo Rong , Chen Yu

张德润, 罗蓉, 陈彧

To evaluate the microscopic properties of DCLR-modified asphalt and its matchability with the typical aggregates,Wilhelmy Plate Method was used to measure the surface energies of 3 different direct-coal-liquefaction residue(DCLR) modified asphalts,1 natural-asphalt-modified asphalt and 1 base asphalt based on the theory of surface free energy(SFE).Then the SFE parameters corresponding to advancing process and receding process were determined,respectively.Subsequently,with the SFE parameters of 2 typical aggregates obtained from Vapor Sorption Method,the cohesive bond energies of all 5 asphalts were calculated as well as the adhesive bond energies between asphalts and aggregates with and without water presence.Eventually,the properties of anti cohesive fracture,healing of DCLR-modified asphalt and properties of water stability,anti adhesive fracture and healing of typical aggregate combination were quantitatively evaluated through comparing with those of the natural-asphalt-modified asphalt and the base asphalt.The results show that the water stabilities of the 3 selected DCLR-modified asphalts combined with aggregate are better than that of the base asphalt and 7 # DCLR-modified asphalt has the best performances of the cohesive fracture resistance and the adhesive fracture resistance.

为评估煤直接液化残渣(DCLR)改性沥青的微观性质及其与典型集料的匹配性,基于表面自由能理论,采用插板法对3种DCLR改性沥青、1种天然改性沥青以及1种基质沥青的表面能进行测试,并分别得到对应前进及后退过程的2套表面能参数,结合蒸气吸附法测试得到的2种典型集料的表面能参数,进一步计算得到沥青自身的内聚结合能以及有水、无水条件下沥青-集料组合的黏附结合能。通过与天然改性沥青及基质沥青对比,采用表面能指标量化评价了DCLR改性沥青的愈合及抗内聚开裂性能及其与典型集料组合的愈合性能、抗黏附开裂性能以及水稳定性。结果表明:3种DCLR改性沥青与集料组合的水稳定性均优于基质沥青,且7 # DCLR改性沥青的抗内聚开裂性能及与集料组合的抗黏附开裂性能最好。

... 对于插板法得到的接触角,该模型按照以下步骤计算沥青表面能^[3]:首先联立杨氏方程(式(2))和Dupre公式(式(3)),得到式(4): ...

... 一般而言, ER1和ER2值越大,则沥青混合料水稳定性越好^[2,3] ...

... 选用蒸馏水、丙三醇和乙二醇作为表面能测试试剂,其表面能参数如表2所示^[3] ...

2002

0.0

... 然而该测试模型仍然存在以下两方面的不足:①后退过程测试的接触角及其对应的表面能并不可靠:沥青在撤出试剂时表面会裹覆一层液体膜,液体膜产生的扩张压力导致沥青表面特性发生改变^[4],从而造成明显的滞后效应^[5,6]并影响后退接触角的大小 ...

... 3 基于膜压力的计算模型基于膜压力的计算模型可直接求解表面能总量,推导过程^[4]为:将前进接触角#cod#x003b8 ...

... 2 基于膜压力的计算模型在基于膜压力的计算模型中,粘附功直接由表面能总量表示,结合Good提出的粘附功表达式^[4,9], Wa12和 Wc11可表达为: ...

1994

0.0

1998

0.0

1999

0.0

2003

0.0

1992

0.0

... 使用Good参数 φ可以表示物质间的粘附功^[9],如式(12)所示: ...

... 2 基于膜压力的计算模型在基于膜压力的计算模型中,粘附功直接由表面能总量表示,结合Good提出的粘附功表达式^[4,9], Wa12和 Wc11可表达为: ...

2009

0.0

. 2009, (6):50-53

Research on moisture susceptibility of SMA pavement

SMA路面抗水损害研究

Gao Wei , Guo Li-li , Han Sen

高巍, 郭黎黎, 韩森

水损害是沥青混凝土路面主要破坏形式之一.以西安咸阳国际机场专用高速公路为依托,通过试验验证了SMA混合料良好的抗水损害性能,并对混合料中粗、细集料以及沥青用量对水稳定性的影响进行了分析.最后,结合SMA混合料骨架结构和脉动水压力理论,分析说明了SMA路面良好的抗水损害性能.

... 2 基于表面能的沥青混合料水稳定性指标沥青路面的水损害,一般是指渗入路面内部结构空隙或微裂缝中的水在真空负压力或孔隙水压力作用下,逐渐将沥青从集料表面剥离,进而导致沥青混合料丧失粘结力并被破坏的过程^[10] ...

0.0

... 3 ASTM D3625水煮法试验参照ASTM D3625水煮法规程^[11],将蒸馏水装入洁净的烧杯中加热至微沸状态,选定13 ...