考虑离心力的定量式扇形静压转台承载力建模

引用本文

刘志峰, 浑连明, 殷亚文, 王建华, 罗宗兰, 董湘敏. 考虑离心力的定量式扇形静压转台承载力建模[J].吉林大学学报（工学版）, 2017,47(6): 1791-1795
LIU Zhi-feng, HUN Lian-ming, YIN Ya-wen, WANG Jian-hua, LUO Zong-lan, DONG Xiang-min. Modeling of bearing capacity of fixed hydrostatic turntable considering centrifugal force[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1791-1795 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706016
Permissions

考虑离心力的定量式扇形静压转台承载力建模

刘志峰¹, 浑连明¹, 殷亚文¹, 王建华¹, 罗宗兰¹, 董湘敏²

1.北京工业大学先进制造技术北京市重点实验室,北京 100124

2.承德石油高等专科学校机械工程系,河北承德 067000

作者简介:刘志峰(1973-),男,教授,博士.研究方向:数字化设计与制造,机械传动,制造信息化与信息管理系统,CIMS.E-mail:lzf@bjut.edu.cn

基金:国家自然科学基金项目(51575009); 国家科技重大专项项目(2014ZX04010-011); 北京工业大学京华人才项目

摘要

针对定量式扇形静压油垫承载力计算未考虑离心力因素的影响,且传统计算方法缺乏试验验证的问题,首先推导得到考虑离心力的扇形静压支承油垫承载力模型,而后建立了转台的整体动力学模型,设计了液体静压转台试验方案,并进行了试验研究。通过理论计算值与试验值的对比分析表明,两者变化趋势基本一致,误差范围在比较合理的范围内,验证了考虑离心力的扇形油垫承载力计算模型和整体动力学方程的可行性。本文所建的模型及分析结论可以为实际生产及转台的服役性能提供理论支持。

关键词: 机械设计; 机械传动; 扇形油垫; 承载力; 离心力

中图分类号:TH137 文献标志码:A 文章编号:1671-5497(2017)06-1791-05

Modeling of bearing capacity of fixed hydrostatic turntable considering centrifugal force

LIU Zhi-feng¹, HUN Lian-ming¹, YIN Ya-wen¹, WANG Jian-hua¹, LUO Zong-lan¹, DONG Xiang-min²

1.Beijing Key Laboratory of Advanced Manufacturing Technology, Beijing University of Technology, Beijing 100124,China

2.Department of Mechanical Engineering, Chengde Petroleum College,Chengde 067000, China

Abstract

The quantitative sector fan-shaped oil pad bearing capacity calculation does not take into account the effect of centrifugal force, and the traditional calculation method lacks experimental verification. To solve this problem, first, the bearing capacity model of the fan-shaped static bearing oil pad is derived, in which the centrifugal force is considered. Then the overall dynamic model of the turntable is established. The hydrostatic turntable experiment scheme is designed, and experiments are carried out. The experiment results are basically in agreement with theoretical calculation results that the error is within reasonable range, which verifies the feasibility of the model and the overall kinetic equation for the calculation of the bearing capacity of the fan-shaped oil pad considering of the centrifugal force. The model and the analysis conclusion of this work may provide theoretical support for practical production and the service performance of the turntable.

Keyword: mechanical design; mechanical driver; fan-shaped oil pad; bearing capacity; centrifugal force

Show Figures

0 引言

液体静压转台是利用有压力的流体使相对运动的两个表面分开并借助流体静压来承载。由于运动副之间完全被油膜隔开, 所以运动副间的摩擦力大大减小, 同时其承载能力、运动精度和寿命却大大提高。正因为液体静压支承的诸多优点, 使其在机床、航空航天、船舶等行业得到了广泛应用。

在国内, 陈燕生^[1]将扇形多垫平面推力轴承的油垫简化为矩形, 求得其承载力、刚度等参数的计算公式, 但未考虑离心力因素。刘震北^[2]对圆形静压推力轴承的承载力进行研究时计入了惯性效应的影响, 指出高速工况下惯性效应对承载力的影响不应忽视, 但并未对扇形多垫平面推力轴承进行研究。于晓东等^[3]分析了转速对多油垫转台油腔压力、油腔流量、油膜厚度和工作台浮升等参数的影响规律, 得到了速度与扇形腔多油垫静压推力轴承润滑参数的关系, 为静压推力轴承的设计、润滑和试验提供了基础数据。叶红玲等^[4]从Navier-Stokes方程入手建立了液体静压导轨系统转台的动力学方程并针对不同油腔数目、封油边油膜厚度和油液黏度, 对液体静压转台启动时的动态特性进行了分析。刘志峰等^[5]推导了雷诺方程并求解了静压支承油垫非线性承载力, 计算分析了表面粗糙度、油垫初始油膜厚度等因素对静压转台动态的特性影响规律。在国外, Garratt等^[6]针对流体可压缩的高速空气轴承建立了一个考虑离心力的修正雷诺方程, 对固定间隙的空气轴承进行了稳态性能分析, 并建立了轴承的非线性动力学模型, 分析了空气轴承在一定转速范围内, 不同频率和幅值的力对轴承的影响。Prabhu等^[7]通过求解包含惯性项的雷诺方程分析了多垫推力轴承在转动及偏载情况下的承载力、流量和刚度并分析了油垫尺寸对承载力和流量的影响。Srinivasan^[8]研究了黏度和压力变化对液体静压轴承静态和动态承载力的影响。Kozdora等^[9]利用CFD方法研究了静压推力轴承油膜的压力、温度、速度场的分布。但上述研究均未深入分析离心力对静压推力轴承承载力的影响。

虽然目前关于静压转台研究的文献较多, 但考虑离心力效应的比较少, 且传统的计算方法缺乏试验验证。本文首先推导了考虑离心力的定量式扇形油垫承载力模型, 而后建立了转台的动力学模型, 最后通过试验研究了供油量、转速、加载位置对油膜厚度的影响规律。

1 考虑离心力的扇形油垫承载力计算

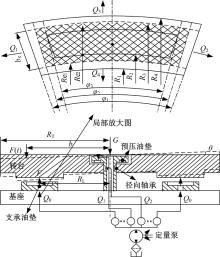
某重型定量式供油静压转台结构示意图如图1所示, 上图为扇形油垫结构简图。润滑油经各中心进油孔流入扇形油垫后, 经四周封油边流出。图中, 阴影部分表示单个扇形油垫的有效承载面积; Q₁、Q₂、Q₃、Q₄分别为油垫各封油边的润滑油流量; R₁、R₂、R₃、R₄分别为油垫及油腔各圆弧边对应的半径; R_e1、R_e2为油垫的有效半径; R_L为各油垫中心到转台中心的距离; $\begin{matrix} φ_{1} \end{matrix}$ 为扇形油垫对应的圆心角; $\begin{matrix} φ_{2} \end{matrix}$ 为有效承载面积区对应的圆心角; $\begin{matrix} φ_{3} \end{matrix}$ 为油腔对应的圆心角; b_e 为有效承载区径向宽度; F(t)为偏心载荷; b为偏心载荷作用点到转台中心的距离; R_T为转台半径; G为转台自身重力; θ 为转台倾斜角度。

	Figure Option View Download New Window
	图1 液体静压转台结构示意图Fig.1 Schematic diagram of hydrostatic rotary table

假设条件:①润滑油的流动为层流状态; ②润滑油与接触壁面无滑移; ③润滑油压力、密度和黏度沿油膜厚度方向不变; ④润滑油只沿周向和径向流动。根据文献[1]中圆形油腔平面推力轴承承载力计算方法和油腔有效承载面积理论可以得到以下参数。

圆形油腔平面推力轴承在任意半径 $\begin{matrix} r \end{matrix}$ 处, 由离心力作用产生的流量为:

$\begin{matrix} Q_{ω} = \frac{π}{20 μ} ρ h^{3} ω^{2} r^{2} = 0.15 ρ h^{3} ω^{2} r^{2} / μ (1) \end{matrix}$

式中: $\begin{matrix} μ 、 ρ 、 h 、 ω \end{matrix}$ 分别为润滑油动力黏度、润滑油密度、油膜厚度、转台角速度。

扇形油垫的有效夹角为:

$\begin{matrix} φ_{e} = φ_{2} = (φ_{1} + φ_{3}) / 2 (2) \end{matrix}$

有效承载面积外圆半径为:

$\begin{matrix} R_{e 1} = R_{4} \sqrt[]{\frac{1 - (R_{3} / R_{4})^{2}}{2 \ln (R_{4} / R_{3})}} (3) \end{matrix}$

有效承载面积内圆半径为:

$\begin{matrix} R_{e 2} = R_{2} \sqrt[]{\frac{1 - (R_{1} / R_{2})^{2}}{2 \ln (R_{2} / R_{1})}} (4) \end{matrix}$

有效承载区径向宽度为:

$\begin{matrix} b_{e} = R_{e 1} - R_{e 2} (5) \end{matrix}$

当量半径为:

$\begin{matrix} R_{e} = (R_{e 1} + R_{e 2}) / 2 (6) \end{matrix}$

在此基础上, 建立考虑离心力的扇形油垫承载力数学模型。

润滑油总流量为:

$\begin{matrix} \begin{matrix} Q_{0} = Q_{1} + Q_{2} + Q_{3} + Q_{4} = \\ \frac{b_{e} h^{3} Δp}{3 μ (φ_{1} - φ_{3}) R_{e}} + \frac{φ_{e} h^{3} Δp}{12 μ} \times \\ \frac{\ln (R_{4} R_{2} / R_{1} R_{3})}{\ln (R_{4} / R_{3}) In (R_{2} / R_{1})} + \\ \frac{0.15 ρ ω^{2} φ_{e} h^{3}}{6 μ} (R_{e 1}^{2} - R_{e 2}^{2}) = \\ C_{1} \frac{h^{3} Δp}{μ} + C_{2} \frac{h^{3} Δp}{μ} + C_{3} \frac{h^{3}}{μ} (7) \end{matrix} \end{matrix}$

式中: $\begin{matrix} Δp \end{matrix}$ 为胸腔内压强;

$\begin{matrix} \begin{matrix} C_{1} = \frac{b_{e}}{3 (φ_{1} - φ_{3}) R_{e}}; \\ C_{2} = \frac{φ_{e} \ln (R_{4} R_{2} / R_{3} R_{1})}{12 \ln (R_{4} / R_{3}) \ln (R_{2} / R_{1})}; \\ C_{3} = 0.05 ρ φ_{e} b_{e} R_{e} ω^{2} 。 \end{matrix} \end{matrix}$

对于定量式供油静压轴承, $\begin{matrix} Q_{0} \end{matrix}$ 始终为一定值。当油膜间隙一定时, 油腔内压强为:

$\begin{matrix} Δp = \frac{μ Q_{0} - C_{3} h^{3}}{(C_{1} + C_{2}) h^{3}} (8) \end{matrix}$

扇形油垫的有效承载面积为:

$\begin{matrix} A_{e} = \frac{φ_{e}}{2} [R_{4}^{2} \frac{1 - (R_{3} / R_{4})^{2}}{2 \ln (R_{4} / R_{3})} - R_{2}^{2} \frac{1 - (R_{1} / R_{2})^{2}}{2 \ln (R_{2} / R_{1})}] (9) \end{matrix}$

单个扇形油垫的承载力为:

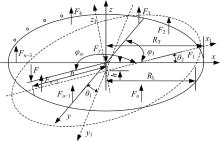
$\begin{matrix} F_{s} = \frac{μ Q_{0} A_{e}}{(C_{1} + C_{2}) h^{3}} - \frac{C_{3} A_{e}}{C_{1} + C_{2}} (10) \end{matrix}$

2 静压转台动力学建模

图2为静压转台受力简图, 转台由 $\begin{matrix} n \end{matrix}$ 个均布扇形油垫支承, 支承力分别为 $\begin{matrix} F_{si}, \end{matrix}$ 它们与加力点和转台中心的连线的夹角 $\begin{matrix} φ_{i} = 2 πi / (n - 1), i = 1, 2, \dots, n; F_{y} \end{matrix}$ 为预压油垫的支承力; R_T为转台半径; $\begin{matrix} ω \end{matrix}$ 为转台的转速; $\begin{matrix} F \end{matrix}$ 为外载, 与 $\begin{matrix} x \end{matrix}$ 轴的角度为为φ_ω, 到转台中心的距离为b; h为转台油膜厚度; $\begin{matrix} θ_{x} 、 θ_{y} \end{matrix}$ 分别为转台在偏心载荷作用下对x轴和y轴的倾角。认为转台自身不发生变形, 所以在偏心载荷下的动力学方程为:

$\begin{matrix} \{\begin{matrix} \overset{n}{\sum_{i = 1}} F_{si} - F_{y} - F - mg = m \frac{d^{2} h}{d t^{2}} \\ \overset{n}{\sum_{i = 1}} F_{si} R_{L} \sin (φ_{i}) - Fbs i n (φ_{ω} + ωt) = J \frac{d^{2} θ_{x}}{d t^{2}} \\ \overset{n}{\sum_{i = 1}} F_{si} R_{L} \cos (φ_{i}) - Fbcos (φ_{ω} + ωt) = J \frac{d^{2} θ_{y}}{d t^{2}} \end{matrix} (11) \end{matrix}$

式中: m为转台质量; J为在偏心力F作用下转台的转动惯量。

	Figure Option View Download New Window
	图2 静压转台受力示意图Fig.2 Schematic diagram of forces on hydrostatic rotary table

3 试验验证

3.1 试验系统组成及工作原理

重型液体静压转台试验系统如图3所示。该系统由静压转台、液压系统、动力系统、检测系统和控制系统组成。

	Figure Option View Download New Window
	图3 液体静压转台试验系统Fig.3 Hydrostatic rotary table experimental system

重型液压转台试验系统工作原理为:润滑油经液压系统流入静压回转工作台导轨油腔, 为主轴提供润滑并使静压转台处于静压工作状态; 润滑油经静压导轨封油边流出, 再经液压系统流回油箱; 控制系统通过控制驱动供油泵和电机的频率来控制润滑油流量和转台转速; 通过温控系统控制油箱内润滑油的温度; 通过人机界面, 用户可以对静压转台进行操作并能直接读取相关数据。

3.2 试验方案

开启温控油箱, 使润滑油温度恒定。分别对以下3种工况进行试验研究。方案1:载荷保持不变, 转速为20 r/min工况下, 改变润滑油供油量, 通过电涡流位移传感器采集数据, 以研究供油量对油膜厚度的影响规律。方案2:空载工况下, 保持润滑油供油量不变, 改变转台转速, 以研究转速对油膜厚度的影响规律。方案3:转台静止工况, 保持润滑油供油量不变, 改变载荷加载位置, 以研究不同加载位置对油膜厚度的影响规律。试验验证现场如图4所示。

	Figure Option View Download New Window
	图4 试验验证现场Fig.4 Experimental verification site

3.3 试验结果分析

将试验值与理论计算值进行对比分析, 验证定量式供油扇形油垫承载力计算公式和动力学方程的可行性。该静压转台相关参数如下:φ ₁=13π /90=0.4538; φ ₂=0.384; φ ₃=π /10=0.3142; R₁=850 mm; R₂=917 mm; R₃=983 mm; R₄=1050 mm; ρ =917 kg/m³; μ =0.0193 Pa· s; n=12; 经计算得R_e=949.7 mm, b_e=132.6 mm。

3.3.1 载荷一定时, 油膜厚度与供油量的关系

表1为载荷8.7 t、转速为20 r/min、润滑油温度为28.6 ℃时, 不同供油量下油膜厚度的理论计算值与试验值的对比。由表1可知, 试验值与理论计算值变化趋势一致, 两者之间的误差在16%以内; 随着供油量增大, 油膜厚度增大; 供油量为3 L/min时, 误差最大, 为16%。

表1 供油量与油膜厚度对比 Table 1 Comparison of oil flow and oil film thickness

3.3.2 转速与油膜厚度的关系

表2为润滑油温度28.5℃、不加载, 不同转速时油膜厚度理论值与试验值对比。由表2可知:随着转速的提高, 油膜厚度发生变化, 但幅度较小。由此表明, 离心力对油膜厚度有一定影响。转速为60 r/min时, 误差最大, 为18%。

表2 转速与油膜厚度对比 Table 2 Comparison of speed and oil film thickness

3.3.3 不同加载位置与油膜厚度的关系

表3为载荷8.7 t、润滑油温度为28.4 ℃、静压转台静止, 不同加载位置(见图4)条件下理论值与试验值的对比。由表3可知, 两者变化趋势一致, 误差范围在15%以内; 随着加载位置的增大, 油膜厚度增加; 最大误差为15%, 最小误差为10%。

表3 不同加载位置与油膜厚度对比 Table 3 Comparison of oil film thickness and loading position

以上3种不同试验方案中, 测得的油膜厚度试验值均小于理论计算值, 原因是:考虑离心力的扇形油垫承载力建模是基于理想假设, 而实际的静压转台工况比较复杂, 受温度、加工装配误差、静压导轨弹性变形等因素影响较大。油膜厚度是通过电涡流位移传感器采集, 在读取数据时也会产生一定的误差。

试验结果表明, 3种试验方案下, 试验值与理论计算值变化趋势一致, 且误差在比较合理的范围内, 验证了定量式扇形油垫承载力模型和整体动力学方程的可行性。

4 结论

(1)针对液体静压转台油垫承载力传统公式中没有考虑离心力因素的影响, 推导了计入离心力的定量式扇形油垫承载力计算模型, 并建立了静压转台的整体动力学模型。

(2)设计了3种试验方案, 对液体静压转台进行试验研究。建立了油膜厚度随供油量增加而增加大规律曲线; 在一定的转速范围内, 随着转速的提高, 油膜厚度减小, 但变化幅度不大; 对于偏载时, 加载点位置离转台中心越远, 油膜厚度越大。

(3)通过试验值与理论计算值的对比分析, 两者变化趋势一致, 且误差在较合理范围内, 验证了定量式扇形油垫承载力计算模型和整体动力学模型的可行性, 对液体静压转台的实际生产和服役性能评估提供了理论指导。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	陈燕生. 液体静压支承原理和设计[M]. 北京: 国防业出版社, 1980: 273-276. [本文引用:1]
[2]	刘震北. 静压推力轴承惯性效应分析[J]. 现代机械, 1991(4): 6-10. Liu Zhen-bei. Analysis of the bearing inertial effect[J]. Morden Machinery, 1991(4): 6-10. [本文引用:1]
[3]	于晓东, 邱志新, 李欢欢, 等. 扇形腔多油垫静压推力轴承润滑性能速度特性[J]. 热能动力工程, 2013, 28(3): 296-300. Yu Xiao-dong, Qiu Zhi-xin, Li Huan-huan, et al. Lubrication performance and speed characteristics of the hydrostatic thrust bearing with a fan shaped cavity[J]. Journal of Engineering for Thermal Energy and Power, 2013, 28(3): 296-300. [本文引用:1]
[4]	叶红玲, 郑小龙, 沈静娴, 等. 液体静压导轨转台轴向振动的动力学建模与分析[J]. 工程力学, 2012, 29(3): 218-225. Ye Hong-ling, Zheng Xiao-long, Shen Jing-xian. Dynamic modeling and analysis of the axial vibration of the hydrostatic slide table[J]. Engineering Mechanics, 2012, 29(3): 218-225. [本文引用:1]
[5]	刘志峰, 湛承鹏, 赵永胜, 等. 定量式静压转台动态特性建模与影响因素分析[J]. 机械工程学报, 2015, 51(19): 75-83. Liu Zhi-feng, Zhan Cheng-peng, Zhao Yong-sheng, et al. Modeling and analysis of the dynamic behaviors of a quantitative type hydrostatic rotary table[J]. Journal of Mechanical Engineering, 2015, 51(19): 75-83. [本文引用:1]
[6]	Garratt J E, Hibberd S, Cliffe K A, et al. Centrifugal inertia effects in high-speed hydrostatic air thrust bearings[J]. Engineering Mathematics, 2012, 76(1): 59-80. [本文引用:1]
[7]	Prabhu T J, Ganesan N. Effects of tilt on the characteristics of multirecess hydrostatic thrust bearings under conditions of no rotations[J]. Wear, 1983, 92(2): 269-277. [本文引用:1]
[8]	Srinivasan V. Analysis of static and dynamic load on hydrostatic bearing with variable viscosity and pressure[J]. Indian Journal of Science and Technology, 2013, 6(Sup. ): 4777-4782. [本文引用:1]
[9]	Kozdora M, Drabkova S. Numerical modelling of the flow in the annular muti-recess hydrostatic thrust bearing using CFD methods[J]. EDP Sciences, 2013, 45: 1-6. [本文引用:1]

1980

0.0

... 在国内,陈燕生^[1]将扇形多垫平面推力轴承的油垫简化为矩形,求得其承载力、刚度等参数的计算公式,但未考虑离心力因素 ...

1991

0.0

... 刘震北^[2]对圆形静压推力轴承的承载力进行研究时计入了惯性效应的影响,指出高速工况下惯性效应对承载力的影响不应忽视,但并未对扇形多垫平面推力轴承进行研究 ...

2013

0.0

. 2013, 28(3):296-300

Lubrication performance and speed characteristics of the hydrostatic thrust bearing with a fan shaped cavity

扇形腔多油垫静压推力轴承润滑性能速度特性

Yu Xiao-dong , Qiu Zhi-xin , Li Huan-huan

于晓东, 邱志新, 李欢欢

扇形腔多油垫静压推力轴承润滑性能受速度的显著影响,设计不当会引起润滑油膜破裂和干摩擦,严重时导致静压支承摩擦失效.针对此问题,运用流体动力学和润滑理论对油腔压力、油腔流量、油膜厚度等参数的速度特性进行数值分析,得到了速度对扇形腔多油垫静压推力轴承润滑参数的影响规律,避免静压支承摩擦失效的发生.研究结果表明:随着旋转工作台转速升高,惯性带油和离心力作用而甩出的润滑油油量增大,流出油腔的油流量增多,引起油腔压力下降,致使油膜厚度变薄,出现油膜破裂和干摩擦,导致静压支承摩擦失效.该研究为静压推力轴承的设计、润滑和实验提供基础数据,实现对静压推力轴承润滑性能速度特性的预测,达到减少经济损失的目的.

... 于晓东等^[3]分析了转速对多油垫转台油腔压力、油腔流量、油膜厚度和工作台浮升等参数的影响规律,得到了速度与扇形腔多油垫静压推力轴承润滑参数的关系,为静压推力轴承的设计、润滑和试验提供了基础数据 ...

2012

0.0

. 2012, 29(3):218-225

Dynamic modeling and analysis of the axial vibration of the hydrostatic slide table

液体静压导轨转台轴向振动的动力学建模与分析

Ye Hong-ling , Zheng Xiao-long , Shen Jing-xian.

叶红玲, 郑小龙, 沈静娴

... 叶红玲等^[4]从Navier-Stokes方程入手建立了液体静压导轨系统转台的动力学方程并针对不同油腔数目、封油边油膜厚度和油液黏度,对液体静压转台启动时的动态特性进行了分析 ...

2015

0.0

. 2015, 51(19):75-83

Modeling and analysis of the dynamic behaviors of a quantitative type hydrostatic rotary table

定量式静压转台动态特性建模与影响因素分析

Liu Zhi-feng , Zhan Cheng-peng , Zhao Yong-sheng

刘志峰, 湛承鹏, 赵永胜

... 刘志峰等^[5]推导了雷诺方程并求解了静压支承油垫非线性承载力,计算分析了表面粗糙度、油垫初始油膜厚度等因素对静压转台动态的特性影响规律 ...

2012

0.0

... 在国外,Garratt等^[6]针对流体可压缩的高速空气轴承建立了一个考虑离心力的修正雷诺方程,对固定间隙的空气轴承进行了稳态性能分析,并建立了轴承的非线性动力学模型,分析了空气轴承在一定转速范围内,不同频率和幅值的力对轴承的影响 ...

1983

0.0

... Prabhu等^[7]通过求解包含惯性项的雷诺方程分析了多垫推力轴承在转动及偏载情况下的承载力、流量和刚度并分析了油垫尺寸对承载力和流量的影响 ...

2013

0.0

... Srinivasan^[8]研究了黏度和压力变化对液体静压轴承静态和动态承载力的影响 ...

2013

0.0

... Kozdora等^[9]利用CFD方法研究了静压推力轴承油膜的压力、温度、速度场的分布 ...