在车间设施动态布局设计中, 规划阶段产品需求由市场预测方法获知, 可认为设施间的物流量在一定的范围内波动, 具有模糊性。投产阶段可追溯与产品相关的历史信息数据来预测实际物料需求, 具有随机性且服从正态分布。本文在考虑产品需求不确定的前提下, 在每个生产阶段根据产品需求的变化来实施设施重布局。本文选择设施面积不等的生产车间为研究对象, 研究连续空间布局, 车间内设施采用多行布置, 为避免设定设备分行数布置对最优布局方案搜索的局限^[17], 提出了自动换行策略。为简化模型, 问题假设条件如下:

(1)整个生产周期共由t个生产阶段组成;

(2)所有设施在车间矩形边界内平行坐标轴放置, 所有设施外形轮廓为矩形, 忽略设施的外形细节, 且几何参数已知, 其值随着生产阶段发生变化;

(3)每台设施重布局成本、占地面积均为已知变量, 但其值随着生产阶段变化;

(4)设施之间的物料运输方向平行于坐标轴。

确定产品需求下DFLP模型是指在各个生产阶段内的物流量是确定值的前提下构建DFLP问题数学模型, 目标函数一般为最小化物料搬运成本和重布局费用, 具体表示如下:

min MRC=∑t=1T∑k=1q∑j=k+1qFjktDjkt+∑t=2T∑k=1qRktZkt1

式中:MRC为最小车间内物料搬运总成本; Fjkt为在给定的t生产阶段从设施j与设施k之间的所需物流量; Djkt为给定的t生产阶段设施j到设施k的物料搬运距离; Rkt为给定的t生产阶段内, 设施k的重布局费用; Zkt为二进制变量, Zkt=1表示在t生产阶段内发生重布局, Zkt=0表示t时间段内未发生重布局, q为设施总数。

不确定产品需求下DFLP模型是指各个生产阶段内的物流量是不确定值的前提下构建DFLP问题数学模型。综上所述, 本文采用模糊随机变量描述不确定性, 即生产周期各个阶段内设施间的物流量既具有模糊性, 又具有随机性, 且服从正态分布。首先, 本文将每个生产阶段设施之间的物流量定义为模糊随机变量 D-~pt。布局问题模型由确定产品需求下转变至模糊随机产品需求下, 大大增加了解决问题的难度。其次, 采用Xu等^[15]提出的方法首先将模糊随机变量 D-~pt转变成梯形模糊变量 W-~pt, 其中 D-~pt=(d_m, τ (d), d_n), τ (d)服从正态分布N(μ , σ ²), 且相应的概率密度函数为ψ _τ x= 12πσexp(- (x-μ)22σ), d_m, d_n根据经验或者已形成的知识数据确定范围; 另外, 梯形模糊变量 W-~pt=(d_m, d_, d-, d_n)可以认为是三角模糊变量 S-~pt=(d_l, d_v, d_r)的特例, 当 d_= d-=d_v, 梯形模糊变量就转化为三角模糊变量。然后, 将 D-~pt=(d_m, τ (d), d_n)模糊随机变量转变为 α, γ置信层面上的梯形模糊变量 W-~pt=(d_m, d_, d-, d_n), α 为模糊变量的决策者置信度水平, γ 为随机变量决策者置信度水平。最后再进一步采用Heilpern等^[18]提出的期望值算子方法, 将 α, γ置信层面上的梯形模糊变量 W-~pt=(d_m, d_, d-, d_n)转变成确定值EV D-~ptα, γ, 表达式如下:

EVD-~ptα, γ=12(d_-∫dmfD-~ptα, γ(x)dx)+(d-+∫dmgD-~ptα, γ(x)dx)](2)

式中: fD-~ptα, γ(x)、 gD-~ptα, γ(x)分别为增、减函数, EV D-~ptα, γ为t生产阶段物流量的期望值。

基于上述模糊随机变量最终转变至确定值的过程分析, 式(1)转变为式(3):

min MRFC=∑t=1T∑k=1q∑j=k+1qEVD-~ptα, γDjkt+∑t=2T∑k=1qRktZkt3

1.4.1 空间约束

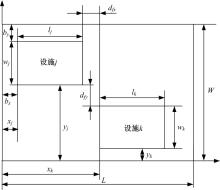
车间布局中空间约束一般考虑二维平面, 因高度空间一般较为宽裕, 本文暂不考虑, 布局示意图如图1所示。为避免设施超越车间边界和相邻设施之间相互重叠, 车间布局中空间约束主要为以下两种约束:①邻近车间边界的设施空间约束, 详见公式(4)~(7); ②任意相邻设施间的空间约束, 详见公式(8)~(11)。

xj≥bx4

xj+lj≤L-bx5

yj≥by6

yj+wj≤W-by7

式中:x_j、y_j为任意设施j的起点坐标, 即如图1所示设施左下角起点坐标; b_x、b_y为设施与车间设施布局的界限预留的人员活动或物流运输空间; L、W分别为车间设施布局的总长和总宽; l_j、w_i分别为车间设施对应的长和宽。

lj+dfx≤xj-xk8

xj-xk≤L-lk-bx9

wk+dfy≤yj-yk10

yj-yk≤W-wj-by11

式中:x_k、y_k为任意设施k的起点坐标, d_fx为设施之间沿x轴方向最小间距; d_fy为设施之间沿y轴方向最小间距。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 车间设施布局示意图Fig.1 Two-dimensional facility layout diagram

1.4.2 逻辑约束

在跨越t个生产阶段后, 设施位置可能需要重布局, 所以设施中心坐标在相邻生产阶段的布局应尽可能的靠近, 避免中断生产, 有效降低重布局成本。若设施中心坐标在相邻生产阶段的间距为0, 则不需要重布局。若相邻时间段间距超过一定约束条件, 则需要重布局, 具体逻辑约束如式(12)~(15):

xit-xit-1≥KZit12

yit-yit-1≥KZit13

lit-lit-1≥KZit14

wit-wit-1≥KZit15

式中: Zit表示t生产阶段设施i采用重布局, 取值为1, 反之为0; K最大取值为i, j设施间在x轴方向或在y轴方向的中心坐标间的最小间距。

1.5.1 设施之间物料总搬运距离

设施之间物料总搬运距离为t个生产阶段内设施之间的搬运距离之和。最小化设施之间的物料总搬运距离, 可有效降低搬运成本, 提高搬运效率。由于设施简化为面积不等的矩形方块, 设施之间的距离为设施中心坐标在标准坐标系下的轴距之和, 即为曼哈顿距离。相同设施之间的中心坐标重合, 故距离为0。最小化设施之间的物料总搬运距离表达式如下:

min DjkT=∑t=1T∑k=1q∑j=k+1qxjt-xkt+yjt-ykt16

1.5.2 车间面积利用率最大

在车间设施布局问题中, 一方面考虑到设施布置紧凑性原则, 另一方面设施在运输、安装、运行的过程中需要预留一定的动态空间, 所以将面积利用率最大作为优化目标之一, 表达式如下:

maxA=SL/S17

SL=[(xjmax+lj/2)-(xkmin+lk/2)]·(yjmax+wj/2)-(ykmin+wk/2)](18)

式中:S为车间总面积, minS=L· W; S_L为有效利用面积; x_jmax、y_jmax对应中心坐标最大的设施j, x_kmin、y_kmin对应中心坐标最小的设施k。由于上述其他目标优化问题主要求解目标最小值问题, 故将问题转化为求空置面积利用率最小的优化问题, 具体表达式如下:

minr=(S-SL)/S19

式中:K=S-S_L为空置面积最小; r为空置面积利用率。

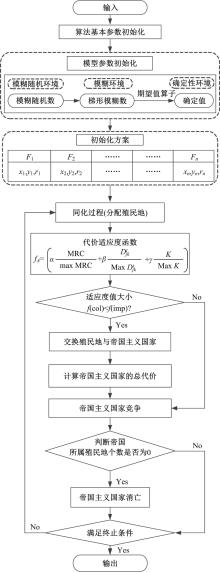
殖民竞争算法是在模拟人类社会殖民竞争过程的基础上提出的一种元启发式算法。与粒子群算法、遗传算法相比, 殖民竞争算法具有以下特点:收敛速度较快, 不易陷入局部收敛, 适合解决大规模的优化问题^[15]。其大致流程主要包括:帝国初始化、帝国与殖民地同化、代价计算、殖民竞争、弱国消亡、强弱国聚合。

由于算法的初始解的质量直接影响算法的计算效率, 本文提出基于系统化布置设计方法确定设施间的方位及邻接关系, 从而获得质量相对较高的初始解, 再结合车间边界范围内随机生成的解, 共同组成初始解集。初始化方案步骤如下所示:

步骤1对设施间物流量分为A, E, I, O, U, X六个等级进行。

步骤2依据步骤1中分析出物流作业量化关系获得设施的紧密程度, 得到w个具体的布局形式。

步骤3对w个布局方式进行编码, 得到初始个体N_w。

步骤4通过结合车间边界范围内随机产生的解N_s与步骤3获得的初始个体N_w共同组成初始种群。

殖民算法中初始化帝国表示解决方案, 类似于粒子群算法, 每个粒子代表一种布局方案。在t个生产阶段内, 设种群中前N_imp个作为殖民国家, 其余为殖民地。每个国家及其所管辖殖民地的编码是一个三维向量(x, y, r), 其中(x, y)表示设施的平面位置坐标, r为重布局标记, 采用二进制变量表示。根据逻辑约束式(12)~(15), 判断相邻生产阶段, 即t阶段与t-1阶段设施间距超过一定约束条件, 则需要重布局, r=1, 否则r=0。车间共有q组设施, 每个粒子中包含2q个平面坐标和1个重布局标记, 具体表达式如下:

Ic=(x1t, y1t, x2t, y2t, …, xqt, yqt, rt)20

本文要解决最小化物料搬运成本和重布局费用、设施之间物料总搬运距离、车间空置面积三个多目标优化问题。考虑到在实际问题研究中, 多目标优化问题的目标函数值可能存在数量级别以及量纲上的差距, 例如在本文的布局优化问题中, 目标函数物料运输成本最小化目标函数在10⁵数量级, 而设施之间物料总搬运距离一般在10⁴数量级, 车间空置面积一般在10³数量级, 简单地将目标函数值加和, 则目标函数值较小的容易被忽略, 并且在后期的算法优化中, 容易造成算法的局部收敛。因此, 构造一个相对合理的代价函数, 同时也要对目标函数值进行量纲归一化处理。考虑到目标的优先级, 依据经验分配不同的权重系数, 可得代价函数如下:

fA=αMRCmaxMRC+βDjktmaxDjkt+γKmaxK21

式中:α , β , γ 为各个目标权重, 且满足α +β +γ =1。

基于上述描述, 针对不等面积设施摆放区域, 总装车间设施动态布局多目标优化算法实施全过程如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 基于位置的殖民竞争算法实施流程图Fig.2 The position-based colonial competitive algorithm flow chart

算法实施过程具体步骤如下:

第1步:参数初始化, 初始化帝国种群规模, 依据3.1初始化方案所述方法, 选取N_w个初始个体作为殖民国家个数N_imp, 其余N_col个为殖民地等。按照国家势力大小划分殖民地, 定义殖民国家规范化代价值为:

CN=cN-max{ci}(22)

式中:c_N为第N个殖民国家的代价值, max{c_i}为所有殖民国家代价值的最大值, C_N为第N个殖民国家规范化的代价值。

每个国家占有的殖民地的概率计算如下:

PN=CN∑i=1NimpCi23

则分配给每个帝国的殖民地数量为:

N·CN=round{PN·Ncol}(24)

式中:N· C_N为第N个殖民国家所占有的殖民地的数量。

第2步:参照1.3节所述的方法, 将模糊随机变量转化为模糊变量, 然后转化为在确定产品需求下的变量。设置必要参数, 将不确定产品需求下参数值转变为确定产品需求下参数值。

第3步:同化过程。将殖民地移向其所属殖民国家, 到达新位置距离为x, 均匀分布随机数x~U(0, β × d), d为殖民地与帝国之间的距离, β > 1使得殖民地从两侧向殖民国家靠近, 一般取β =2易获得全局最优解。同化公式如下:

Xnew= Xold+U(0, β × d)× O(25)

式中:{O}为殖民地到殖民国家的方向向量。

第4步:根据式(21)计算殖民地和殖民国家代价函数大小。若殖民地适应度值小于殖民国家, 交换两者的位置。若殖民地适应度值大于殖民国家, 将殖民地移向相关的殖民国家。

第5步:计算所有帝国的总代价, 即根据式(26)计算N个殖民国家及其所管辖的M个殖民地的总代价值。

TCk=cost(N)+φ·meancost(M)(26)

式中:0< φ < 1, 通常φ 取0.1。

第6步:殖民国家竞争。比较帝国的总代价值, 将较弱的帝国的殖民地给予比较强的帝国, 更新强国的代价值。定义帝国的国家规范化的总代价值为:

N·TCN=TCN-max{TCi}(27)

式中:max{TC_i}为所有帝国中最大的总代价值, N· TC_N为规范化的总代价值。

每个帝国的势力如下:

PTN=N·TCN∑i=1NimpN·TCi28

由每个帝国的势力值组成势力向量P

P=PT1, PT2, …, PTNimp29

创建一个与势力向量同维度的概率矩阵R

R=R1, R2, …, RNimp30

式中:R₁, …, RNimp~U(0, 1), 可得殖民地占有率向量D

D=P-R=PT1-R1, PT2-R2, …, PTNimp-RNimp31

向量D中元素最大值将可以占有最弱帝国的殖民地。

第7步:迭代N次后, 判断是否有帝国所属殖民地个数是否为0。若为0, 则帝国消亡; 若没有, 则跳转到第8步。

第8步:得到全局最优解后, 若满足终止条件, 则跳转至第9步; 否则, 转至第3步。

第9步:输出优化结果, 结束。

在传统的航空总装车间布局规划中, 产品需求假设过于理想化、布局设计过程较多依赖人为经验, 缺乏有效的量化布局设计优化方法。本文为进一步验证布局方法的有效性以及算法的合理性, 结合某大型航空装备总装车间设施动态布局实例, 在不确定需求下进行车间设施布局规划。

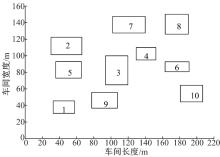
总装车间共有10处设施组位置待确定, 主要包括成附件、专用设备、标准件、耗材、自产零件、工装设施、运载设备、线边库存等放置区域。车间设计总长为220 m, 宽为160 m, 相邻设施间x, y方向最大间距为5 m(如图1所示d_fx, d_fy间距), 为考虑实际车间物流通道空间, 设施与车间边界x, y方向最大距离为6.5 m(如图1所示b_x, b_y间距)。设施起始坐标, 即左下角坐标如表1, 表2所示, 整个装配周期共分为5个生产阶段, 不同生产阶段内, 设施占地面积不同(如表3所示)。由于文章篇幅有限, 仅列出t=1阶段10台设施间的物流量(如表4, 表5所示, 数据来源于某航空装备总装厂)。对于相邻生产阶段之间可能涉及到设施的重布局问题, 每台设施重布局的费用已知, 如表6所示。

表1

Table 1

表1(Table 1)

表1 车间设施1~5起始坐标 Table 1 Initial position values for facilities 1~5 设施号 F1 F2 F3 F4 F5 横坐标 25.25 25 95.5 125.75 160 纵坐标 21.75 105.5 70.5 102.5 130

表1 车间设施1~5起始坐标 Table 1 Initial position values for facilities 1~5

表2

Table 2

表2(Table 2)

表2 车间设施6~10起始坐标 Table 2 Initial position values for facilities 6~10 设施号 F6 F7 F8 F9 F10 横坐标 170.25 100 35 176.75 72.5 纵坐标 80.5 130 80 40 30.5

表2 车间设施6~10起始坐标 Table 2 Initial position values for facilities 6~10

表3

Table 3

表3(Table 3)

表3 设施占地面积 Table 3 Facilities required length and width m2 设施号 设施占地面积(L× W) t=1 t=2 t=3 t=4 t=5 F1 35× 20 20× 15 16× 15 10× 12 25× 15 F2 30× 20 16× 13 11× 13 9× 10 18× 15 F3 40× 25 16× 15 16× 15 16× 15 16× 35 F4 32× 25 10× 12 8× 10 12× 10 23× 15 F5 32× 24 15× 14 17× 20 0× 0 18× 20 F6 23× 18 18× 12 16× 9 10× 9 28× 12 F7 22× 14 8× 10 12× 14 8× 12 8× 12 F8 41× 21 17× 19 18× 11 0× 0 20× 25 F9 38× 20 16× 16 25× 13 13× 12 16× 20 F10 25× 35 25× 20 16× 10 0× 0 30× 19

表3 设施占地面积 Table 3 Facilities required length and width m2

表4

Table 4

表4(Table 4)

表4 1~5设施与所有设施之间的物料需求量(t=1) Table 4 The fuzzy random material demands between any two facilities (1-5) at the first period 设施号 F1 F2 F3 F4 F5 F1 — (50, τ 12, 70) (42, τ 13, 65) (7, τ 14, 10) (35, τ 15, 46) τ 12~N(62, 10) τ 13~N(58, 8) τ 14~N(8, 3) τ 15~N(41, 6) F2 (50, τ 21, 70) — (10, τ 23, 25) (20, τ 24, 32) (5, τ 25, 10) τ 21~N(62, 10) τ 23~N(19, 4) τ 24~N(28, 5) τ 25~N(8, 5) F3 (42, τ 31, 65) (10, τ 32, 25) — (20, τ 34, 32) 0 τ 31~N(58, 8) τ 32~N(19, 4) τ 34~N(28, 5) F4 (7, τ 41, 10) (20, τ 42, 32) (20, τ 43, 32) — 0 τ 41~N(8, 3) τ 42~N(28, 5) τ 43~N(28, 5) F5 (35, τ 51, 46) (5, τ 52, 10) 0 0 — τ 51~N(41, 6) τ 52~N(8, 5) F6 (5, τ 61, 8) (4, τ 62, 7) (15, τ 63, 25) (6, τ 64, 9) (2, τ 65, 7) τ 61~N(6, 2) τ 62~N(6, 2) τ 63~N(19, 4) τ 64~N(7, 2) τ 65~N(4, 2) F7 (4, τ 71, 7) (5, τ 72, 8) (15, τ 73, 25) (20, τ 74, 28) (6, τ 75, 9) τ 71~N(6, 2) τ 72~N(6, 2) τ 73~N(19, 2) τ 74~N(23, 5) τ 75~N(7, 2) F8 (90, τ 81, 120) (45, τ 82, 70) (55, τ 83, 75) (25, τ 84, 42) (5, τ 85, 10) τ 81~N(110, 20) τ 82~N(60, 6) τ 83~N(65, 7) τ 84~N(35, 4) τ 85~N(35, 4) F9 (120, τ 91, 150) (200, τ 92, 220) (90, τ 93, 120) (60, τ 94, 80) (20, τ 95, 30) τ 91~N(142, 20) τ 92~N(217, 10) τ 93~N(117, 8) τ 94~N(75, 6) τ 95~N(25, 6) F10 (7, τ 101, 10) (5, τ 102, 8) 0 (5, τ 104, 8) (4, τ 105, 7) τ 101~N(8, 3) τ 102~N(6, 3) τ 104~N(6, 3) τ 105~N(6, 2) 注:“ 0” 表示设施间物流量为0; “ — ” 表示设施本身之间不存在物料流动。

表4 1~5设施与所有设施之间的物料需求量(t=1) Table 4 The fuzzy random material demands between any two facilities (1-5) at the first period

表5

Table 5

表5(Table 5)

表5 6~10设施与所有设施之间的物料需求量(t=1) Table 5 The fuzzy random material demands between any two facilities (6-10) at the first period 设施号 F6 F7 F8 F9 F10 F1 (5, τ 16, 8) (4, τ 17, 7) (90, τ 18, 120) (120, τ 19, 150) (7, τ 101, 10) τ 16~N(6, 2) τ 17~N(6, 2) τ 18~N(118, 20) τ 19~N(142, 20) τ 101~N(8, 3) F2 (4, τ 26, 7) (5, τ 27, 8) (45, τ 28, 70) (200, τ 29, 220) (5, τ 210, 8) τ 26~N(6, 2) τ 27~N(6, 2) τ 28~N(60, 10) τ 29~N(217, 10) τ 210~N(6, 3) F3 (15, τ 36, 25) (15, τ 37, 25) (55, τ 38, 75) (90, τ 39, 120) 0 τ 36~N(19, 4) τ 37~N(19, 2) τ 38~N(65, 7) τ 39~N(117, 12) F4 (6, τ 46, 9) (20, τ 47, 28) (25, τ 48, 42) (60, τ 49, 80) (5, τ 410, 8) τ 46~N(7, 2) τ 47~N(23, 5) τ 48~N(35, 4) τ 49~N(75, 6) τ 410~N(6, 3) F5 (2, τ 56, 7) (6, τ 57, 9) (5, τ 58, 10) (20, τ 59, 30) (4, τ 510, 7) τ 56~N(4, 2) τ 57~N(7, 2) τ 58~N(8, 4) τ 59~N(25, 6) τ 510~N(6, 2) F6 — (16, τ 67, 25) (20, τ 68, 30) (40, τ 69, 55) (6, τ 610, 9) τ 67~N(20, 4) τ 68~N(25, 3) τ 69~N(45, 5) τ 610~N(7, 2) F7 (16, τ 76, 25) — (5, τ 78, 10) (6, τ 79, 9) (3, τ 710, 9) τ 76~N(20, 4) τ 78~N(8, 4) τ 79~N(7, 2) τ 710~N(6, 3) F8 (20, τ 86, 30) (5, τ 87, 10) — (16, τ 89, 28) (5, τ 810, 10) τ 86~N(25, 3) τ 87~N(8, 4) τ 89 ~N(22, 4) τ 810~N(8, 2) F9 (10, τ 96, 55) (6, τ 97, 9) (16, τ 98, 28) — 0 τ 96~N(45, 5) τ 97~N(7, 2) τ 98~N(22, 4) F10 (6, τ 106, 9) (3, τ 107, 9) (5, τ 108, 10) 0 — τ 106~N(7, 2) τ 107~N(6, 3) τ 108~N(8, 2)

表5 6~10设施与所有设施之间的物料需求量(t=1) Table 5 The fuzzy random material demands between any two facilities (6-10) at the first period

表6

Table 6

表6(Table 6)

表6 每个阶段每台设施重布局费用 Table 6 The arrangement costs for each facilities at each period 1× 105 CNY 设施号 t=1 t=2 t=3 t=4 t=5 F1 197 78 261 128 89 F2 106 183 97 293 196 F3 98 153 125 276 65 F4 145 204 110 100 140 F5 156 93 40 78 132 F6 203 176 152 102 95 F7 85 235 74 151 126 F8 164 251 122 88 46 F9 37 186 137 87 132 F10 126 201 92 119 76

表6 每个阶段每台设施重布局费用 Table 6 The arrangement costs for each facilities at each period 1× 105 CNY

从企业的总体效益出发, 考虑不确定需求车间设施动态布局更贴近实际, 同时有效降低企业成本。在大型航空装备总装车间布局规划阶段, 对于大型航空装备的市场需求一般由市场预测获知, 可视作在一定范围内波动, 存在模糊性, 同时大型航空装备由多种成件、部件、标准件、附件及耗材等共同装配完成, 产品种类有限, 在投产阶段产品需求(即物料需求量)可由历史数据(例如:BOM表、物料管理清单、质检数据等)预测出来, 具有随机性, 且服从正态分布。本文采用模糊随机变量 D-~pt来描述不确定性需求, 其中 D-~pt=(d_m, τ (d), d_n), 模糊随机变量 D-~pt的模糊性通过三角模糊数字上限d_m与下限d_n之间。随机变量τ (d)服从正态分布N(μ , σ ²)。

为了进一步说明模糊随机模型的合理性, 采用基于位置的殖民竞争算法分别将确定产品需求下模型、随机产品需求下模型与模糊随机产品需求下模型计算的结果进行对比, 其中确定产品需求下物流量定义为模糊数范围内最大值、最小值的平均值, 随机产品需求下的物流量定义为正态分布的期望值, 模糊随机产品需求下物流量采用1.3节所述方法, 将模糊随机物流量转换为确定物流量。从表7对比中看出, 确定产品需求下计算的物流搬运成本平均值、最优值分别比随机产品需求下物流搬运成本高4.22%和5.04%; 随机产品需求下的物流搬运成本平均值、最优值分别比模糊随机产品需求随机产品需求下搬运成本均值高2.71%和4.02%; 由表8可知, 随机产品需求下物料搬运距离平均值、最优值分别比确定产品需求下高1.81%和0.12%; 比模糊随机产品需求随机产品需求下高1.82%, 0.91%; 由表9可知, 随机产品需求下空置面积平均值、最优值分别比模糊随机产品需求随机产品需求下高2.3%和2.5%; 比确定产品需求下高0.93%和1.01%。因此可以得出结论, 模糊随机产品需求随机产品需求下的模型, 比模糊环境、随机产品需求下的模型更能提供最小化的物料搬运成本、总搬运距离和空置面积。

表7

Table 7

表7(Table 7)

表7 不同产品需求下的物料搬运成本对比 Table 7 Model comparison in transportation costs 1× 105 CNY 条件 最差值 平均值 最优值 确定产品需求 7.9784 7.9065 7.8349 随机产品需求 7.8246 7.7919 7.7592 模糊随机产品需求 7.7133 7.5860 7.4587

表7 不同产品需求下的物料搬运成本对比 Table 7 Model comparison in transportation costs 1× 105 CNY

表8

Table 8

表8(Table 8)

表8 不同产品需求下的物料总搬运距离 Table 8 Model comparison in total distance 1× 104m 条件 最差值 平均值 最优值 确定产品需求 6.5391 6.4435 6.3478 随机产品需求 6.5453 6.4524 6.3549 模糊随机产品需求 6.3782 6.3378 6.2973

表8 不同产品需求下的物料总搬运距离 Table 8 Model comparison in total distance 1× 104m

表9

Table 9

表9(Table 9)

表9 不同产品需求下的空置面积 Table 9 Model comparison in vacant area 1× 103m2 条件 最差值 平均值 最优值 确定产品需求 1.3258 1.3115 1.2972 随机产品需求 1.3372 1.3237 1.3102 模糊随机产品需求 1.3095 1.2937 1.2778

表9 不同产品需求下的空置面积 Table 9 Model comparison in vacant area 1× 103m2

采用基于位置的殖民竞争算法和粒子群优化算法同时对模型求解。在本文实例中粒子群迭代次数设为30次, 种群规模为50, 加速系数为2, 惯性因子0.6。依次对3个目标最优值、最差值、平均值分别做比较, 详见表10、表11、表12。其中在物料搬运成本目标中, 粒子群算法的平均值、最优值分别比殖民竞争算法高1.42%和0.68%; 在物料总搬运距离目标中, 粒子群算法的平均值、最优值分别比殖民竞争算法2.27%和2.79%; 在空置面积目标中, 粒子群算法的平均值、最优值分别比殖民竞争算法1.9%和2.5%。实例表明殖民算法比粒子群算法寻优能力更强。由于物料搬运成本、比搬运距离、空置面积相对重要, 依据权重指标分析, 取权重系数α =0.5, β =0.3, γ =0.2。初始坐标即t=0时刻车间不等面积设施平面布局, 布局示意图如图3所示。经算法优化后获得t=5时刻不等面积车间设施平面布局, 如表13、表14所示, 布局示意图如图4所示。

表10

Table 10

表10(Table 10)

表10 不同算法下的物料搬运成本 Table 10 Algorithm comparison in transportation costs 1× 105 CNY 条件 最差值 平均值 最优值 帝国竞争算法 7.6675 7.5631 7.4587 粒子群算法 7.8327 7.6711 7.5095

表10 不同算法下的物料搬运成本 Table 10 Algorithm comparison in transportation costs 1× 105 CNY

表11

Table 11

表11(Table 11)

表11 不同算法下的物料总搬运距离 Table 11 Algorithm comparison in total distance 1× 104m 条件 最差值 平均值 最优值 帝国竞争算法 6.3871 6.3422 6.2973 粒子群算法 6.5003 6.4868 6.4732

表11 不同算法下的物料总搬运距离 Table 11 Algorithm comparison in total distance 1× 104m

表12

Table 12

表12(Table 12)

表12 不同算法下的空置面积 Table 12 Algorithm comparison in vacant area 1× 103m2 条件 最差值 平均值 最优值 帝国竞争算法 1.2987 1.2660 1.2333 粒子群算法 1.3153 1.2901 1.2649

表12 不同算法下的空置面积 Table 12 Algorithm comparison in vacant area 1× 103m2

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 t=0时刻车间不等面积设施平面布局Fig.3 Unequal-area facilities layout at the 1st period

表13

Table 13

表13(Table 13)

表13 车间设施1~5起始坐标(t=5) Table 13 facilities layout position value at 5th period 设施号 F1 F2 F3 F4 F5 横坐标 32.61 30.07 93.65 129.32 35.58 纵坐标 30.58 101.37 64.96 95.01 73.04

表13 车间设施1~5起始坐标(t=5) Table 13 facilities layout position value at 5th period

表14

Table 14

表14(Table 14)

表14 车间设施6~10起始坐标(t=5) Table 14 facilities layout position value at 5th period 设施号 F6 F7 F8 F9 F10 横坐标 163.00 101.80 163.12 77.5 180.83 纵坐标 80.79 127.52 126.12 36.78 44.37

表14 车间设施6~10起始坐标(t=5) Table 14 facilities layout position value at 5th period

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 t=5时刻车间不等面积设施平面布局Fig.4 The optimal solution for unequal-area facilities layout at the 5th period