作者简介:付文智(1960-),男,教授,博士.研究方向:无模成形及数字化制造.E-mail:fwz@jlu.edu.cn
为了掌握新型舰船用材料1561铝合金板类件的成形规律,通过拉伸试验获得了1561铝合金的机械性能特性曲线。通过有限元软件模拟了1561铝合金的多点成形和卸载过程,结果表明:1561铝合金板料在成形过程中易起皱,具有较大的回弹量。采用回弹补偿法和多道次成形工序对某船用曲面件进行多点成形试验,并通过三维扫描和Geomagic软件对成形精度进行了分析,结果表明:采用回弹补偿法和多道次成形方法可以很好地解决曲线的回弹和起皱问题。
In order to know the formability of 1561 aluminum alloy sheet as a new ship material,its mechanical properties were obtained by tensile test. The multi-point forming and unloading process of aluminum alloy sheet was simulated by finite element software ABAQUS. Simulation results showed that 1561 aluminum alloy material was easy to wrinkle during the forming process and had a large springback. Three-dimensional scanning and Geomagic analysis were carried out, and the results verify the feasibility of using the springback compensation to compensate the springback and multi-steps forming method to solve the winkling in the multi-point forming of 1561 aluminum alloy. At the same time, it is shown that simulation results are reliable.
随着船舶制造向轻量化、高速化、大型化方向发展, 具有小密度、大比强度、较好稳定性的铝镁合金成为替代船用钢材的优选材料[1, 2]。目前在船舶制造中5083铝合金使用得较多, 但焊接后的矫形处理对制造精度的影响较大[3]。1561铝合金(俄罗斯牌号)[4]相比5083铝合金具体更高的强度, 采用1561铝合金作为船用材料将会提高舰船的质量和性能。多点成形[5, 6, 7]是一种适用于复杂件成形的柔性成形技术[8, 9, 10, 11], 它是由一系列紧密排列、高度可调的基本体单元组成[12]。相比于传统模具成形, 一套离散化的多点模具通过数字化控制即可成形多种形状和尺寸的曲面件, 省去了传统模具制造、调试等成本, 真正实现了“ 一机多用” 的构想, 适用于曲面件的板料成形。
目前, 国内、外对1561铝合金成形性的研究鲜有报道, 为了迎合新产品开发的需要, 本文利用有限元软件对某船用典型曲面件进行了多点成形数值模拟, 研究了1561铝合金的回弹补偿, 掌握了1561铝合金成形件的回弹规律, 并对模拟结果进行了试验验证, 结合3DSS三维扫描和Geomagic软件分析对成形件的成形精度进行了分析。
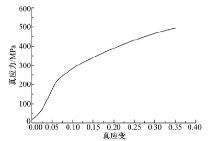
为了使多点成形过程模拟计算得到的结果更精确, 使计算结果能够指导实际生产, 按照《GB/T228.1— 2010》[13]设计试样, 如图1所示, 在电子万能试验机上进行室温拉伸断裂试验。表1为1561铝合金的拉伸试验数据, 可见, 1561铝合金的抗拉强度和屈服强度的平均值分别为345.9和266.67 MPa; 弹性模量E为67.516 GPa; 延伸率平均值为21.8%。1561铝合金的真实应力-应变曲线如图2所示。
| 表1 1561铝合金力学性能试验数据 Table 1 1561 aluminum alloy mechanical properties test data |
为了更好地分析1561铝合金板料的多点成形过程, 利用有限元分析方法中的动态显式算法对1561铝合金的加载成形过程进行计算, 同时结合静态隐式算法对卸载回弹过程进行数值模拟。图3为多点成形有限元模型, 由板料、聚氨酯弹性垫以及上、下多点模具组成。成形板料选用厚度为3 mm的1561铝合金。多点模具形面尺寸为500 mm× 700 mm; 基本体单元为10 mm× 10 mm; 冲头半径为8 mm, 板料形状如图3所示。与板料变形量相比, 冲头变形量非常小, 故冲头设为刚体单元。同时为了简化计算模型, 假设板料为各向同性。上、下多点冲头采用R3D4单元划分网格, 网格单元尺寸为2 mm。板料采用S4R壳单元划分网格, 网格单元尺寸为3 mm。聚氨酯弹性垫采用C3D8R单元划分网格, 网格单元尺寸为3 mm。聚氨酯弹性垫与板料和多点模具之间的摩擦因数取0.3。
图4为本文开发成形的某船外板零件所需板料。为了叙述方便, 设板料宽度中心长度方向为X方向; 长度中心宽度方向为Y方向; 板料平面法线方向为Z方向, 如图4所示。
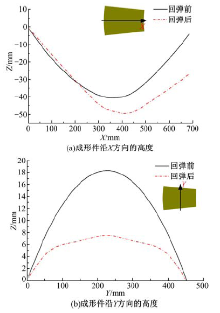
图5为成形得到的某船外板多点成形件回弹前、后的轮廓对比图, 其中网格图为回弹前工件轮廓图。图6为成形件卸载前、后沿X和Y方向的高度值, 可以发现, 1561铝合金在卸载前、后回弹较大, 前、后形状差别较大, 其中Y方向形状波动起伏不光滑, 发生了起皱, X方向曲面过渡平顺。由此可得, 零件在Y方向较难成形, 皱纹沿着X方向。
由此可见, 1561铝合金的成形件具有较大的回弹量, 且与目标件在X和Y方向的回弹量不同, 因此应采用差异补偿法, 令X和Y方向的形面补偿系数不同。回弹补偿法是通过对模具形面进行预修正, 对模具施加与回弹方向相反的补偿量, 使卸载后的曲面接近目标形状。
对于双曲率零件, 由于零件各个方向曲率不一致, 导致X和Y方向的回弹量不同, 因此X与Y方向的补偿量不同。补偿面上任一位置高度Z的确定方法为:假设目标曲面件上任一点的高度值Z'为h, X方向型面补偿系数为m, Y方向型面补偿系数为n, 则零件的回弹补偿量计算公式为:
合理的变形路径能够使变形板料受力均匀, 变形均匀, 而且能够避免成形缺陷的产生, 获得成形效果良好的零件。板料沿理想路径发生变形, 任意时刻t的形变为[14]:
U(X, t)=Q(t)· Diag[λ α (t)(t)]· QT(t) (2)
式中:Q(t)为正交旋转张量; Diag[λ α (t)(t)]为Hencky应变的主值组成的对角张量, λ α (t)(t)为U(X, t)的主值, α (t)为变形参量。
通过建立泛函方程, 采用数值方法构造的中间构形为:
式中:“ :” 为张量计算符号。
构造的中间构形的单元节点坐标计算公式为:
式中:tΩ e为t时刻构形的体积; Xnode为初始构形中单元的节点坐标; U、分别为数值方法计算出的和理想路径的中间构形变形张量。
通过式(4)可得到t时刻的中间构形。因初始构形及中间构形都是按照理想路径设计, 因此通过式(4)可得到最优成形路径。通过选取变形量不同的最优成形路径上的中间构形, 并通过数值仿真计算, 可得到多道次成形的优化成形路径, 最终确定的目标件成形路径依次为X0.5Y1.2、X0.7Y1.2、X0.9Y1.4、X1.0Y1.6。
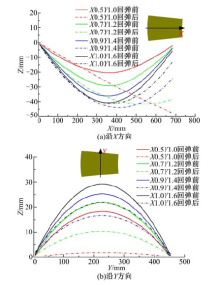
采用差异补偿法补偿多点型面, 并进行一次成形和四道次成形, 其成形对比如图7所示; 零件卸载前、后X和Y方向的高度值如图8所示。图7(a)所示的一次成形零件中部发生起皱, 而图7(b)所示的四道次成形零件过渡平顺, 质量良好, 皱纹完全消失。这是由于多点模具成形采用一次成形方法时, 材料一次性变形较大, 增加回弹补偿量后, 成形深度增加, 容易超过材料一次成形所允许的最大变形量, 在无压边力作用下成形较易起皱。利用多点模具高度可调的优点, 采用多道次成形方法, 每次成形深度较小, 使板料各部分变形在变形过程中最大限度地均匀化, 最终达到目标件尺寸, 可得到质量较高的目标件。由图8可以看出:
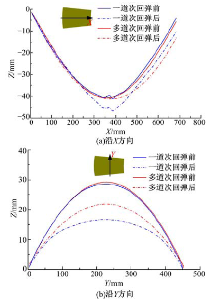 | 图8 不同成形路径下成形件沿中线的高度值Fig.8 Height values of forming part along center line under different forming paths |
成形件在卸载回弹后在Y方向的回弹量较大, 在X方向回弹量较小, 说明, Y方向比X方向较难成形, 需要在Y方向给予更多的补偿量。采用多道次成形方法, 板料每次变形相对一次变形较小, 相对弯曲半径R/t较小, 且变形充分、均匀, 相对于一次成形具有较小的回弹量。
图9为根据模拟结果多次补偿模具型面选取的成形路径依次为X0.5Y1.2、X0.7Y1.2、X0.9Y1.4、X1.0Y1.6四道次成形方法成形零件得到的X方向和X1.0Y1.6四道次成形方法成形零件得到的X方向和Y方向高度值。可以看出, 对于1561铝合金这种回弹较大的材料, 当成形件的变形量较小时, X方向几乎没有变形, 而Y方向轻微变形。采用多道次逐渐过渡的方法成形, 由于每次变形量较小不超过板料成形所允许最大变形量, 成形件表面过渡光顺, 无起皱现象发生, 可得到质量良好的成形件。
对材料为1561铝合金的某船用外板零件在多点成形压力机上进行了多道次成形, 成形件公差要求为± 1 mm。多点成形试验的现场照片如图10所示。
板料尺寸、基本体尺寸与数值模拟相同。成形结果如图11所示, 可以看出, 采用多道次成形工序, 得到的成形件无压痕和起皱等缺陷, 表面连续光滑, 与数值模拟结果吻合。通过样板对成形件检测, 可以看出:形件在X方向和Y方向与目标尺寸吻合较好, 误差较小。以上验证了在1561铝合金多点成形时, 采用回弹补偿法补偿回弹和多道次工艺解决形件起皱的可行性, 也验证了有限元分析结果对生产实践指导的可靠性。
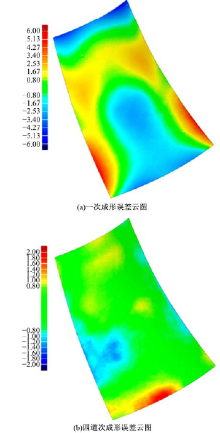
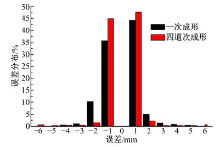
使用3DSS三维扫描仪对一道次和四道次多点成形件进行光学扫描, 获取成形件表面的点云数据; 使用Geomagic分析软件对成形件点云数据与目标件进行比较, 可得到成形件的误差分布规律。成形件的形状误差云图和误差分布图分别如图12和图13所示。由图可以看出, 一次成形件误差80%分布在-1~1 mm, 95%分布在-2~2 mm; 而四道次成形件误差91%分布在-1~1 mm, 96%分布在-2~2 mm。相较于一次成形, 四道次成形件误差较小, 成形质量高, 符合产品要求, 进一步验证了数值模拟的可靠性和采用多道次工序成形1561铝合金的可行性。
(1)新型材料1561铝合金具有较高的屈服强度和较小的弹性模量, 在多点成形后回弹较大, 小变形量在卸载后可基本完全回弹, 因此, 1561铝合金成在成形过程中需给予较大的回弹补偿量。
(2)由数值模拟结果可以看出, 当成形件曲率较大时, 1561铝合金在一次成形时易起皱, 而采用多道次成形方法后, 解决了成形件中心部位起皱的问题, 成形误差± 1 mm的区域由80%提高到91%, 误差减小, 成形精度提高。
(3)通过试验对1561铝合金多点成形的可行性及数值模拟的可靠性进行了验证, 试验结果对1561铝合金零件的实际成形有一定的指导意义。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|