基于模糊隶属度最大似然估计的焊缝隐性缺陷磁记忆信号识别

引用本文

邢海燕, 葛桦, 李思岐, 杨文光, 孙晓军. 基于模糊隶属度最大似然估计的焊缝隐性缺陷磁记忆信号识别[J].吉林大学学报（工学版）, 2017,47(6): 1854-1860
XING Hai-yan, GE Hua, LI Si-qi, YANG Wen-guang, SUN Xiao-jun. Hidden defect metal magnetic memory identification for welded joints based on fuzzy membership and maximum likelihood estimation[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1854-1860 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706025
Permissions

基于模糊隶属度最大似然估计的焊缝隐性缺陷磁记忆信号识别

邢海燕¹, 葛桦¹, 李思岐², 杨文光³, 孙晓军¹

1.东北石油大学机械科学与工程学院, 黑龙江大庆 163318

2.哈尔滨工业大学航天学院,哈尔滨 150001

3.甘肃蓝科石化高新装备股份有限公司,兰州 730070

作者简介:邢海燕(1971-),女,教授,博士.研究方向:石油石化装备损伤检测及可靠性评价,机械设备状态监测与故障诊断.E-mail:xxhhyyhit@163.com

基金:中石油科技创新基金项目(2015D-5006-0602); 国家自然科学基金项目(11272084, 11472076,11072056); 东北石油大学研究生创新科研项目(YJSCX2016-024NEPU); 黑龙江省博士后科研启动基金项目(LBH-Q13035)

摘要

针对磁记忆信号在焊缝残余应力集中、隐性损伤识别和定位上的难题,建立了模糊隶属度最大似然估计识别模型。通过疲劳载荷作用下的Q235钢板状焊缝试件磁记忆检测试验,研究了焊缝残余应力集中、隐性损伤直至宏观断裂整个过程的磁记忆信号变化规律,提取多种磁记忆特征值:峰峰值Δ Hp( y)、梯度最大值 K_max、梯度均值 K_ave、极限状态系数最大值 m_max,引入正态分布函数计算其概率,结合半梯形模糊隶属度函数,建立了焊缝隐性损伤的模糊隶属度最大似然估计识别模型,判断疑似缺陷点进而识别隐性损伤并定位缺陷。结果表明:基于多种特征参数基础上的最大似然模糊隶属度估计结果与实际缺陷位置完全一致,验证了该模型可以有效避免误判的发生,为实际工程中应用磁记忆技术进行焊缝隐性损伤识别和定位提供了新的方法。

关键词: 材料合成与加工工艺; 磁记忆检测; 焊缝隐性损伤; 隶属度函数; 最大似然估计

中图分类号:TG441.7 文献标志码:A 文章编号:1671-5497(2017)06-1854-07

Hidden defect metal magnetic memory identification for welded joints based on fuzzy membership and maximum likelihood estimation

XING Hai-yan¹, GE Hua¹, LI Si-qi², YANG Wen-guang³, SUN Xiao-jun¹

1.School of Mechanical Science and Engineering, Northeast Petroleum University, Daqing 163318,China

2.School of Astronautics, Harbin Institute of Technology, Harbin 150001,China

3.Lanpec Technologies Limited, Lanzhou 730070,China

Abstract

To overcome the difficulty of Metal Magnetic Memory (MMM) technique in identification and location of the hidden defect in welded joints, a method of Maximum Likelihood Estimation (MLE) and fuzzy membership degree is put forward. The feature law of critical hidden damage is studied by fatigue experiment of Q235 steel plate with incompletely penetrated weld joint. Four feature parameters are extracted, that are peak to peak value Δ Hp( y), mean gradient K_ave, maximal gradient K_max, and maximal limit coefficient mmax. The normal distribution function is employed to calculate the probabilities of the four feature parameters. Then, MLE values are obtained to establish the MLE fuzzy membership model. This model can be used to identify the suspected defect position. Results show that the MLE fuzzy membership model can effectively locate the weld defect and provide a new tool of identification and location of weld hidden damage with MMM method.

Keyword: materials synthesis and processing technology; metal magnetic memory(MMM) testing; weld hidden damage; membership functions; maximum likelihood estimation

Show Figures

0 引言

焊缝结构广泛地应用于石油化工、能源电力、航空航天、铁路桥梁等关系国计民生的重要领域, 在焊接过程中局部形成不稳定的热应力场, 冷却后焊缝及热影响区不可避免地存在残余应力集中, 导致在役运行后早期隐性缺陷的产生, 往往成为灾难性事故的导火索。因此, 及早发现早期隐性缺陷, 对于防止突发性重大事故具有重要作用^[1]。相对于涡流、漏磁、超声、射线等传统无损检测技术, 金属磁记忆检测技术基于力磁效应机理, 不仅能够检测宏观损伤, 更能发现早期应力集中和隐性缺陷, 是21世纪比较具有应用前景的无损检测方法之一^[2]。

目前磁记忆检测技术在焊缝检测与信号处理上取得了大量的研究成果。邸新杰等^[3]最先将磁记忆技术应用到焊缝检测上, 建立基于二维谱熵的焊缝裂纹神经网络识别模型。任吉林等^[4]和王进等^[5]利用小波包能量谱对焊接缺陷进行特征分析, 并率先将李萨如图应用到损伤程度的识别上。张卫民等^[6]和刘红光等^[7]建立了地磁场下的焊缝磁偶极子模型, 提出了提取多种磁记忆特征参数表征焊缝缺陷的方法。胥永刚等^[8]将固有时间尺度分解(ITD)应用到磁记忆信号分析中, 实现了齿轮早期故障的特征提取。董丽虹等^[9]对板状试件应力集中、残余应力及缺陷三者之间的关系进行了讨论, 分析了磁记忆信号对不同应力集中程度、疲劳裂纹及残余应力的变化规律。但由于焊缝处存在焊接残余应力, 使得磁记忆检测在识别焊缝隐性缺陷和焊缝残余应力集中上存在困难, 造成目前实际工程中焊缝隐性缺陷精确识别和定位的瓶颈问题。为此, 本文以焊缝疲劳拉伸试验为基础, 对比X射线检测结果, 获取磁记忆信号的临界损伤演化规律, 提取能反映焊缝损伤状态的多种特征参数, 基于最大似然估计及模糊隶属度函数进行焊缝隐性缺陷的精确识别和定位。

1 焊缝磁记忆检测试验

1.1 试验材料和仪器

采用母材为Q235B的板状焊缝试件, 焊丝为H08Mn2SiA, 采用Y型坡口, 打底和盖面均使用氩弧焊, 试件尺寸及测试路线见图1。试件检测区域尺寸为80 mm× 60 mm× 6 mm, 测量线如图1所示, 平均分布的3条测试线间隔为15 mm。试验选用QBG-300高频疲劳试验机, 施加静载50 kN、动载30 kN。每循环到一定千周(kc), 采用俄罗斯动力诊断公司的TSC-2M-8型金属磁记忆仪, 分别沿焊缝横向测试线V₁、V₂、V₃进行检测, 同步进行焊缝缺陷的X射线对比检测。

	Figure Option View Download New Window
	图1 试件尺寸及测试路线Fig.1 Test specimen size and test line

为了准确观测焊缝损伤的演化过程, 焊缝试件按损伤程度分为正常状态和隐性损伤状态两类, 每类50个试件, 共100个试件, 其中隐性损伤为长2~4 mm的隐性裂纹。

1.2 试验结果

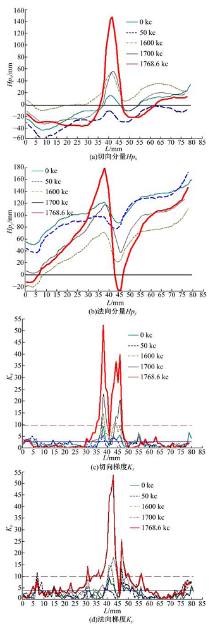
图2为不同疲劳循环次数下的磁记忆信号切向分量Hp_x、法向分量Hp_y、切向梯度K_x和法向梯度K_y对比图。

如图2(a)所示, 磁记忆信号切向分量Hp_x在初始0 kc出现峰值且过零点, 说明磁记忆检测有效反映出焊接残余应力集中的存在; 当循环至50 kc时, Hp_x峰值呈下降趋势且不再过零, 其原因是由于小幅疲劳载荷产生的振动时效起到减小焊缝残余应力集中的作用; 但在1600 kc出现隐性裂纹时, Hp_x峰值并非明显增大; 在1700 kc以后出现宏观裂纹, Hp_x峰值明显增大, 并在1768.6 kc试件断裂时峰值最大且过零点, 满足磁记忆检测判据。图2(b)中的法向信号Hp_y峰值与图2(a)切向信号Hp_x峰值变化规律完全相同。图2(c)(d)中, 切向和法向梯度K_x与K_y随着循环次数的增加, 出现先大后小再大的变化趋势。因此, 在焊缝出现宏观缺陷时, 单凭上述哪一种参数都可以明显识别出来; 但在隐性损伤阶段, 单凭上述哪一种参数都无法准确识别焊接残余应力集中与隐性损伤的区别。

	Figure Option View Download New Window
	图2 不同疲劳循环次数下磁记忆信号对比Fig.2 Contrast of MMM signals under different fatigue cycles

2 基于最大似然模糊隶属度估计的磁记忆信号识别

由于单一的磁记忆特征参数不能准确地判定焊缝残余应力集中与隐性缺陷的区别, 更无法精确定位隐性损伤, 因此需要提取多种特征参数进行综合判断^[10], 考虑到磁记忆信号的分散性和模糊性, 因此从数理统计的角度, 融合多种特征参数, 引入模糊隶属度函数, 采用最大似然估计值进行焊缝残余应力及隐性损伤的精确识别和定位。

2.1 磁记忆信号特征值的提取

通过大量试验观察后, 采用如下4种特征值:

(1)峰峰值Δ Hp(y)

$\begin{matrix} ΔHp (y) = Hp {(y)}_{\max} - Hp {(y)}_{\min} (1) \end{matrix}$

式中:Hp(y)_max、Hp(y)_min分别为磁记忆法向磁场强度最大值和最小值。

(2)梯度最大值K_max

特征信号处Hp(y)曲线的微分值为:

$\begin{matrix} K = dHp (y) / dx (2) \end{matrix}$

本文选用K中的最大值K_max。

(3)平均梯度K_ave

$\begin{matrix} K_{ave} = average (K) (3) \end{matrix}$

(4)梯度极限状态系数m

$\begin{matrix} m = K_{\max} / K_{ave} (4) \end{matrix}$

式中:m值为缺陷处最大梯度K_max与测试区域平均梯度的比值, 比值越高则表示应力集中程度越大, 可以反映缺陷的损伤程度。

2.2 最大似然估计

若总体X属于离散型, 其分布律为:

$\begin{matrix} P {X = x} = p (x; θ), θ \in Θ \end{matrix}$

式中:θ 为待估参数, Θ 为θ 可能取值的范围, 设x₁, x₂, …, x_n为X₁, X₂, …, X_n的一个样本值, 样本取到观察值x₁, x₂, …, x_n的概率, 即事件{X₁=x₁, X₂=x₂, …, X_n=x_n}发生的概率为^[11]:

$L (θ) = L (x_{1}, x_{2}, \dots, x_{n}; θ) = \overset{n}{\prod_{i = 1}} p (x_{i}; θ), θ \in Θ (5)$

如有：

$\overset{n}{\sum_{i = 1}} f (x_{i}; θ') > \overset{n}{\sum_{i = 1}} f (x_{i}; θ″) (6)$

说明估计值取θ '时得到样本值x₁, x₂, …, x_n的可能性大, 此时, θ '可作为待估量的估计值^[12]。其中, θ '、θ ″皆为待估参数。

2.3 正态分布函数概率密度估计

在大量试验数据分析基础上, 焊缝缺陷的特征值近似符合正态分布^[13]。正态分布概率密度函数表达式为:

$\begin{matrix} f (x_{i}; μ, σ) = \frac{1}{\sqrt[]{2 π} σ} \exp [- (x_{i} {- μ)}^{2} / (2 σ^{2})] (7) \end{matrix}$

μ 和σ 的估计值分别为:

$μ = \frac{1}{n} \overset{n}{\sum_{i = 1}} x_{i} (8)$

$σ = \sqrt[]{\frac{1}{n} \overset{n}{\sum_{i = 1}} {(x_{i} - \overset{n}{\sum_{i = 1}} x_{i})}^{2}} (9)$

2.4 模糊隶属度函数

模糊模式识别方法是利用模糊数学中的概念、原理及方法解决分类识别问题^{[14, 15, 16, 17]}, 根据实际问题进行特征提取, 建立模糊集的隶属度函数, 或建立元素之间的模糊相似关系, 并确定这个关系的隶属度函数, 然后运用相关的模糊数学的方法进行分类识别。

模糊模式识别根据实际问题归纳为以下5个步骤:①抽选识别对象的特性指标; ②构造模糊模式的隶属函数; ③构造待识别对象B的隶属函数; ④求出B与A_i(i=1, 2, …, p)的贴近度N(B, A_i); ⑤根据择近原则识别B应归属于哪一个模式。

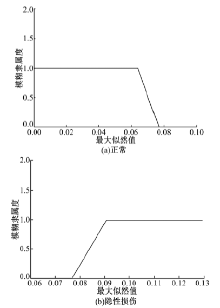
依据试验数据的实际分布规律(见图3), 本文采用半梯形隶属度分布函数^[15], 正常情况采用偏小型半梯形分布, 隐性损伤采用偏大型半梯形分布。

偏小型半梯形分布函数为:

$\begin{matrix} A (x) = \{\begin{matrix} 1, x \leq a \\ \frac{b - x}{b - a}, a < x \leq b \\ 0, x > b \end{matrix} (10) \end{matrix}$

偏大型半梯形分布函数为:

$\begin{matrix} A (x) = \{\begin{matrix} 0, x \leq c \\ \frac{x - c}{d - c}, c < x \leq d \\ 1, x > d \end{matrix} (11) \end{matrix}$

式中:a和b为正常状态的参数; c和d为隐性损伤状态的参数。

2.5 最大似然模糊隶属度估计模型建立

选取未焊透缺陷试件的法向信号进行数据分析, 从中抽取50组数据作为总样本, 其中选取正常情况30组, 隐性损伤20组, 根据式(1)~(4)提取磁记忆特征值。试验数据的平均值和标准差统计如表1所示。

表1 样本的平均值和标准差 Table 1 Mean and standard deviation of sample

根据式(7)~(9), 计算概率密度函数结果如下:

Δ Hp(y)的概率密度分布函数为:

$\begin{matrix} f_{1} (x) = \frac{1}{13.0615 \sqrt[]{2 π}} \times \exp [- \frac{{(x - 29.3520)}^{2}}{2 \times 170.6071}] (12) \end{matrix}$

K_ave的概率密度分布函数:

$\begin{matrix} f_{2} (x) = \frac{1}{2.4243 \sqrt[]{2 π}} \times \exp [- \frac{{(x - 4.3743)}^{2}}{2 \times 5.8775}] (13) \end{matrix}$

K_max的概率密度分布函数:

$\begin{matrix} f_{3} (x) = \frac{1}{4.1784 \sqrt[]{2 π}} \times \exp [- \frac{{(x - 7.6186)}^{2}}{2 \times 17.4593}] (14) \end{matrix}$

m的概率密度分布函数:

$\begin{matrix} f_{4} (x) = \frac{1}{0.4653 \sqrt[]{2 π}} \times \exp [\frac{{(x - 1.8056)}^{2}}{2 \times 0.2148}] (15) \end{matrix}$

将式(12)~(15)进行积分计算, 得到正态分布函数, 然后将正常状态下的30组数据代入上述各个特征值分布函数, 分别求其概率, 并将每一组对应4个特征概率连乘, 获得正常状态下发生的最大似然值。对于隐性损伤情况, 其算法与正常状态的算法一致。正常状态以及隐性损伤状态的特征参数的最大似然值如图3所示。

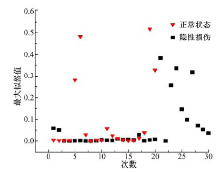	Figure Option View Download New Window
	图3 正常及隐性状态特征参数的最大似然值Fig.3 Maximum likelihood value of normal and hidden state characteristic parameters

利用数理统计方法计算试件正常状态下的最大似然平均值为: $\begin{matrix} {\overset{—}{θ}}_{1} \end{matrix}$ =0.0638; 隐性损伤试件的最大似然平均值为: $\begin{matrix} {\overset{—}{θ}}_{2} \end{matrix}$ =0.0903。据此数理统计结果以及图3分布规律, 在选用半梯形模糊分布时, 正常状态属于偏小型半梯形分布, 隐性损伤属于偏大型半梯形分布。

正常情况下, 以似然平均值 $\begin{matrix} {\overset{—}{θ}}_{1} \end{matrix}$ 为a, 以( $\begin{matrix} {\overset{—}{θ}}_{1} \end{matrix}$ + $\begin{matrix} {\overset{—}{θ}}_{2} \end{matrix}$ )/2为b建立模糊隶属度函数, 表示为:

$\begin{matrix} f (x) = \{\begin{matrix} 1, 0 < x \leq 0.0638 \\ \frac{0.0770 - x}{0.0770 - 0.0638}, 0.0638 < x \leq 0.0770 \\ 0, x > 0.0770 \end{matrix} (16) \end{matrix}$

隐性损伤情况下, 以似然平均值 $\begin{matrix} {\overset{—}{θ}}_{2} \end{matrix}$ 为d, 以( $\begin{matrix} {\overset{—}{θ}}_{1} \end{matrix}$ + $\begin{matrix} {\overset{—}{θ}}_{2} \end{matrix}$ )/2为c建立模糊隶属度函数, 表示为:

$\begin{matrix} f (x) = \{\begin{matrix} 0, 0 < x < 0.0770 \\ \frac{x - 0.0770}{0.0903 - 0.0770}, 0.0770 \leq x < 0.0903 \\ 1, x \geq 0.0903 \end{matrix} (17) \end{matrix}$

式(16)(17)的图形如图4(a)(b)所示。

图4(a)(b)的纵坐标为根据似然值判断损伤状态的隶属度。将似然函数值代入式(16)(17)中, 根据隶属度函数值大小来判断损伤状态的程度。

	Figure Option View Download New Window
	图4 半梯形模糊隶属度函数曲线Fig.4 Semi-trapezoidal fuzzy membership function curve

3 试验验证

3.1 焊缝隐性缺陷识别验证

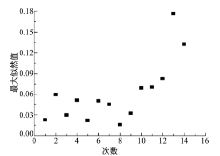
为验证上述模型, 另外选取焊缝试件重复上述试验, 提取了整个试验中14次的磁记忆检测数据, 第12次时出现隐性裂纹。根据式(1)~(4)计算磁记忆特征值, 将各个特征值代入式(12)~(15)进行积分后得到概率, 再根据式(5)得到最大似然值, 结果如图5所示。然后, 将最大似然值代入隶属度函数式(16)和(17), 以此识别正常或损伤状态。

	Figure Option View Download New Window
	图5 验证样本的最大似然值Fig.5 Maximum likelihood value of validation sample

例如根据式(5), 将1~11次磁记忆检测提取出的特征值进行计算, 得到最大似然值均小于0.0703, 根据隶属度函数式(16)可以判断出属于正常状态区间。而将12~14次磁记忆检测提取出的特征值根据式(5)进行计算, 得到最大似然值分别为0.0825、0.1767、0.1325, 根据隶属度函数式(17)可以判断出属于隐性状态区间, 表示试件焊缝出现隐性损伤, 与实际情况相符。

3.2 压力容器焊缝隐性缺陷定位验证

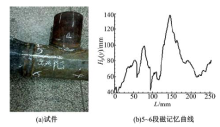
压力容器焊缝结构如图6(a)所示, 其中所测试的焊缝位置为图中的5~6段, 距离端点5的70 mm处预制有夹渣缺陷, 其金属磁记忆检测曲线如图6(b)所示。

	Figure Option View Download New Window
	图6 压力容器焊缝试件及磁记忆曲线Fig.6 Welding specimen of pressure vessel and MMM signal

图6(b)中出现两个较明显的波峰波谷, 一个位于距端点5的70 mm处, 另一个位于距端点5的150 mm处, 这两处分别为疑似点1和2。根据式(1)~(4)提取这两个位置的特征值后, 代入式(12)~(15)进行积分后得到概率, 再根据式(5)得到最大似然值如表2所示。

表2 角焊缝特征值的最大似然估计值 Table 2 Maximum likelihood estimation of characteristic value of fillet weld

将表2中点1和点2的最大似然值分别代入隶属度函数式(16)和(17), 验证结果为疑似点1处的最大似然值为0.18, 根据式(17)计算属于隐性损伤状态的隶属度为1; 疑似点2的最大似然值为0.013, 根据式(16)属于正常状态的隶属度为1, 由此可以判定疑似点1为隐性缺陷位置, 这与压力容器角焊缝实际预制隐性损伤的位置相符。由此可以看出, 仅凭图6上的峰峰值去判断, 疑似点2峰峰值更大, 其损伤程度似乎应该大于疑似点1, 但是实际预制的隐性损伤位置为疑似点1, 因此仅用一种特征值去判断往往会引起误差, 证明综合多种特征参数的最大似然估计方法可以有效避免误判的发生, 在焊缝隐性损伤磁记忆识别和定位中具有较高的有效性和准确性。

4 结论

(1)通过疲劳试验测得的焊缝磁记忆曲线可以发现, 由于焊接残余应力的存在, 导致磁记忆切向和法向信号出现峰值且过零点, 造成识别焊缝残余应力集中和隐性缺陷困难。

(2)由于隐性损伤时对应磁记忆信号呈现分散性和不确定性, 所以有必要从模糊隶属度和数理统计的角度, 提取多种磁记忆特征参数综合识别隐性损伤。

(3)首次建立了焊缝隐性损伤的模糊隶属度最大似然估计模型, 可以精确识别缝隐性损伤并进行定位, 模型验证结果与实际情况相符, 可以有效避免误判的发生。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Jiles D C. A new approach to modeling the magneto mechanical effect[J]. Journal of Applied Physics, 2004, 95(11): 7058-7060. [本文引用:1]
[2]	Doubov A A. Express method of quality control of a spot resistance welding with usage of metal magnetic memory[J]. Thermal Engineering, 1999, 46(5): 369-372. [本文引用:1]
[3]	邸新杰, 李午申, 白世武, 等. 金属磁记忆检测信号的二维谱熵特征[J]. 焊接学报, 2006, 27(11): 69-72. Di Xin-jie, Li Wu-shen, Bai Shi-wu, et al. Two-dimension spectrum entropy feature for metal magnetic memory signal[J]. Transactions of the China Welding Institution, 2006, 27(11): 69-72. [本文引用:1]
[4]	任吉林, 孙金立, 周培, 等. 磁记忆二维检测的研究与工程应用[J]. 机械工程学报, 2013, 49(22): 21-23. Ren Ji-lin, Sun Jin-li, Zhou Pei, et al. Engineering application prospect and research on magnetic memory in two-dimensional testing[J]. Journal of Mechanical Engineering, 2013, 49(22): 21-23. [本文引用:1]
[5]	王进, 任吉林, 任尚坤, 等. 基于金属磁记忆法的焊接缺陷特征值提取[J]. 无损检测, 2009, 31(12): 940-942. Wang Jin, Ren Ji-lin, Ren Shang-kun, et al. Feature extraction of welding defects based on metal magnetic memory[J]. Nondestructive Testing, 2009, 31(12): 940-942. [本文引用:1]
[6]	张卫民, 邱冬超, 于霞, 等. 关于利用金属磁记忆方法进行应力定量化评价问题的讨论[J]. 机械工程学报, 2015, 51(8): 21-24. Zhang Wei-min, Qiu Dong-chao, Yu Xia, et al. Discussion on stress quantitative evaluation using metal magnetic memory method[J]. Journal of Mechanical Engineering, 2015, 51(8): 21-24. [本文引用:1]
[7]	刘红光, 张卫民, 毛新颜, 等. 基于磁记忆检测技术的焊接缺陷多参数识别系统[J]. 制造业自动化, 2009, 31(2): 811-814. Liu Hong-guang, Zhang Wei-min, Mao Xin-yan, et al. Multi-parameter identification system of weld defects based on magnetic memory testing[J]. Manufacturing Automation, 2009, 31(2): 811-814. [本文引用:1]
[8]	胥永刚, 谢志聪, 崔伶丽, 等. 基于ITD的齿轮磁记忆信号特征提取方法的研究[J]. 仪器仪表学报, 2013, 34(3): 671-676. Xu Yong-gang, Xie Zhi-cong, Cui Ling-li, et al. Study on feature extraction method of gear magnetic memory signal based on ITD[J]. Chinese Journal of Scientific Instrument, 2013, 34(3): 671-676. [本文引用:1]
[9]	董丽虹, 徐滨士, 董世运, 等. 金属磁记忆技术表征应力集中、残余应力及缺陷的探讨[J]. 材料工程, 2009(8): 19-23. Dong Li-hong, Xu Bin-shi, Dong Shi-yun, et al. Discussion on characterizing stress concentration residual stress and defect on metal magnetic memory testing[J]. Journal of Materials Engineering, 2009(8): 19-23. [本文引用:1]
[10]	邢海燕, 葛桦, 秦萍, 等. 基于遗传神经网络的焊缝缺陷等级磁记忆定量化研究[J]. 材料科学与工艺, 2015, 23(2): 33-38. Xing Hai-yan, Ge Hua, Qin Ping, et al. MMM quantifying of welded joint defect levels based on BP neural network optimized by genetic algorithm[J]. Materials Science& Technology, 2015, 23(2): 33-38. [本文引用:1]
[11]	Yamamura K. Bayes estimates as an approximation to maximum likelihood estimates[J]. Population Ecology, 2016, 58(1): 45-52. [本文引用:1]
[12]	盛骤. 概率论与数理统计[M]. 北京: 高等教育出版社, 2008. [本文引用:1]
[13]	邢海燕, 党永斌, 王犇, 等. 基于K-近邻隶属度模糊支持向量机的再造抽油杆损伤等级磁记忆定量识别[J]. 石油学报, 2015, 36(11): 1427-1432, 1456. Xing Hai-yan, Dang Yong-bin, Wang Ben, et al. Quantitative MMM identification of damage levels based on KNN FSVM for remanufactured sucker rod[J]. ACTA Petrolei Sinica, 2015, 36(11): 1427-1432, 1456. [本文引用:1]
[14]	陈涛, 李智, 莫玮. 基于模糊模式识别的爆炸物THz光谱识别[J]. 仪器仪表学报, 2012, 33(11): 2480-2486. Chen Tao, Li Zhi, Mo Wei. Identification of terahertz absorption spectra of explosives based on fuzzy pattern recognition[J]. Chinese Journal of Scientific Instrument, 2012, 33(11): 2480-2486. [本文引用:1]
[15]	郝建坤, 黄玮, 刘军, 等. 空间变化PSF非盲去卷积图像复原法综述[J]. 中国光学, 2016, 9(1): 41-50. Hao Jian-kun, Huang Wei, Liu Jun, et al. Review of non-blind deconvolution image restoration based on spatially-varying PSF[J]. Chinese Optics, 2016, 9(1): 41-50. [本文引用:2]
[16]	侯天娇, 郝志成, 朱明, 等. 一种基于FPGA的彩色图像实时增强方法[J]. 液晶与显示, 2016, 31(12): 1161-1167. Hou Tian-jiao, Hao Zhi-cheng, Zhu Ming, et al. Real-time color image enhancement method based on FPGA[J]. Chinese Journal of Liquid Crystal and Displays, 2016, 31(12): 1161-1167. [本文引用:1]
[17]	许廷发, 罗璇, 苏畅, 等. 多帧距离选通图像点扩散函数估计的超分辨率重建[J]. 中国光学, 2016, 9(2): 226-233. Xu Ting-fa, Luo Xuan, Su Chang, et al. Super-resolution reconstruction of multiformat laser range-gated image by the estimate of point-spread function[J]. Chinese Optics, 2016, 9(2): 226-233. [本文引用:1]
[18]	刘亮, 靳斌, 初战平. 基于梯形隶属度模糊算法对电能质量的判断[J]. 电力学报, 2014, 29(2): 110-114. Liu Liang, Jin Bin, Chu Zhan-ping. Based on trapezoidal fuzzy algorithm to determine the quality of electric energy[J]. Journal of Electric Power, 2014, 29(2): 110-114. [本文引用:1]

2004

0.0

... 因此,及早发现早期隐性缺陷,对于防止突发性重大事故具有重要作用^[1] ...

1999

0.0

... 相对于涡流、漏磁、超声、射线等传统无损检测技术,金属磁记忆检测技术基于力磁效应机理,不仅能够检测宏观损伤,更能发现早期应力集中和隐性缺陷,是21世纪比较具有应用前景的无损检测方法之一^[2] ...

2006

0.0

. 2006, 27(11):69-72 DOI:doi:10.3321/j.issn:0253-360X.2006.11.018

Two-dimension spectrum entropy feature for metal magnetic memory signal

金属磁记忆检测信号的二维谱熵特征

Di Xin-jie , Li Wu-shen , Bai Shi-wu

邸新杰, 李午申, 白世武

金属磁记忆检测技术是能够对焊接裂纹进行早期诊断的最具有潜力的无损检测方法之一.以X70管线钢为主要研究对象,研究了其拉伸条件下金属磁记忆检测信号的二维特征谱熵分布规律,通过支持向量机模型,可以实现幅值谱熵和重心频率确定点的位置的分类,结合检测实例,得到了对焊缝中应力集中状态的诊断方法.结果表明,通过磁记忆信号二维特征谱熵的分布可以诊断出材料内部的应力集中状态,从而为利用金属磁记忆检测技术对裂纹萌生状态的诊断提供了依据.

... 邸新杰等^[3]最先将磁记忆技术应用到焊缝检测上,建立基于二维谱熵的焊缝裂纹神经网络识别模型 ...

2013

0.0

. 2013, 49(22):21-23 DOI:doi:10.3901/JME.2013.22.008

Engineering application prospect and research on magnetic memory in two-dimensional testing

磁记忆二维检测的研究与工程应用

Ren Ji-lin , Sun Jin-li , Zhou Pei

任吉林, 孙金立, 周培

摘　要：磁记忆检测作为早期诊断的新兴技术已受到国内外无损检测界广泛关注,但现有的磁记忆检测技术主要以单一方向上的漏磁场信号（法向分量）来进行判断,没有充分利用磁记忆检测信号的全部信息,容易出现漏检、误检等问题.针对该项检测技术的不足,介绍一种将磁记忆检测信号法向分量存在过零点和切向分量存在极大值的特征曲线联合应用的二维检测方法.该方法同时采集法向和切向的磁记忆信号,利用矢量合成法获取切向最大值,然后求取法向、切向分量一阶微分后合成的李萨如图,利用李萨如图的面积对应力状态进行分析,并将自主研制的磁记忆二维仪器应用到工程实践中.实践证明,该二维系统及检测方法能高效地对应力集中进行判定,可望成为实现磁记忆检测定量分析的新方法.

... 任吉林等^[4]和王进等^[5]利用小波包能量谱对焊接缺陷进行特征分析,并率先将李萨如图应用到损伤程度的识别上 ...

2009

0.0

. 2009, 31(12):940-942

Feature extraction of welding defects based on metal magnetic memory

基于金属磁记忆法的焊接缺陷特征值提取

Wang Jin , Ren Ji-lin , Ren Shang-kun

王进, 任吉林, 任尚坤

... 任吉林等^[4]和王进等^[5]利用小波包能量谱对焊接缺陷进行特征分析,并率先将李萨如图应用到损伤程度的识别上 ...

2015

0.0

. 2015, 51(8):21-24 DOI:doi:10.3901/JME.2015.08.009

Discussion on stress quantitative evaluation using metal magnetic memory method

关于利用金属磁记忆方法进行应力定量化评价问题的讨论

Zhang Wei-min , Qiu Dong-chao , Yu Xia

张卫民, 邱冬超, 于霞

对利用金属磁记忆检测技术在应力评价方面的研究现状进行总结，分析磁记忆检测原理和磁机械效应理论之间、应力磁化反转现象和接近定律之间的关系，认为金属磁记忆效应，是稳恒弱磁场激励下的一种力磁效应，符合磁机械效应理论的相关描述和结论。指出弱磁激励情况下力磁关系的非线性、以及检测结果易受众多干扰因素影响的特点，给利用磁记忆检测技术进行应力定量化评价带来实质性困难。磁记忆检测技术的优势，应在研究铁磁材料塑性阶段濒临损伤前的微观缺陷和信号异变的复杂关系以及应力集中和损伤综合作用下异变磁信号的快速和有效识别等方面。

... 张卫民等^[6]和刘红光等^[7]建立了地磁场下的焊缝磁偶极子模型,提出了提取多种磁记忆特征参数表征焊缝缺陷的方法 ...

2009

0.0

. 2009, 31(2):811-814 DOI:doi:10.3969/j.issn.1009-0134.2009.02.003

Multi-parameter identification system of weld defects based on magnetic memory testing

基于磁记忆检测技术的焊接缺陷多参数识别系统

Liu Hong-guang , Zhang Wei-min , Mao Xin-yan

刘红光, 张卫民, 毛新颜

文章采用单一判据在磁记忆检测中容易出现误判和漏判的情况,而综合考虑几种判据则可以提高缺陷判断的准确性.在总结磁记忆技术检测焊接缺陷的多种信号特征基础上,建立了基于神经网络的焊接缺陷多参数识别系统,并对制备的不同类型的焊接缺陷试件进行了识别实验,结果表明该识别系统可对焊接缺陷的位置和类型进行有效识别.

... 张卫民等^[6]和刘红光等^[7]建立了地磁场下的焊缝磁偶极子模型,提出了提取多种磁记忆特征参数表征焊缝缺陷的方法 ...

2013

0.0

... 胥永刚等^[8]将固有时间尺度分解(ITD)应用到磁记忆信号分析中,实现了齿轮早期故障的特征提取 ...

2009

0.0

. 2009, (8):19-23

Discussion on characterizing stress concentration residual stress and defect on metal magnetic memory testing

Dong Li-hong , Xu Bin-shi , Dong Shi-yun

董丽虹, 徐滨士, 董世运

对应力集中、残余应力及缺陷三者之间的关系进行讨论,举例分析磁记忆信号对不同应力集中程度、疲劳裂纹及残余应力的反映.结果表明:金属磁记忆技术适宜表征铁磁材料存在磁导率急剧变化的位置;磁记忆信号能否表征残余应力还需要进一步的深入研究.

... 董丽虹等^[9]对板状试件应力集中、残余应力及缺陷三者之间的关系进行了讨论,分析了磁记忆信号对不同应力集中程度、疲劳裂纹及残余应力的变化规律 ...

2015

0.0

. 2015, 23(2):33-38 DOI:doi:10.11951/j.issn.1005-0299.20150206

MMM quantifying of welded joint defect levels based on BP neural network optimized by genetic algorithm

基于遗传神经网络的焊缝缺陷等级磁记忆定量化研究

Xing Hai-yan , Ge Hua , Qin Ping

邢海燕, 葛桦, 秦萍

In order to quantify defect levels of welded joints by using the metal magnetic memory technology (MMM), fatigue experiments were operated to find the MMM feature law of critical damage. The experiment material is Steel Q345 that is prefabricated with incomplete penetration and slag. In the light of the X ray detection national standard and MMM testing signals, welded joints are divided into four levels: normal, stress concentration, hidden damage and macroscopic damage. BP Neural Network (BPNN) optimized by genetic algorithm is firstly presented to quantify defect levels based on MMM parameters, which indicates that the optimized BPNN is more stable and accurate than BPNN without optimization. This research provides a new scientific tool for practical engineering.

针对金属磁记忆技术的焊缝缺陷等级定量化评定这一难题,通过对预制不同缺陷的Q345焊接试件进行疲劳试验,获得焊缝损伤演化临界状态的磁记忆信号特征规律.首次对照X射线定量检测标准和磁记忆检测结果,将焊缝损伤演化状态分为4个等级,即正常状态、应力集中、隐性损伤和宏观损伤.首次引入遗传算法优化的BP神经网络模型对焊缝等级进行磁记忆定量化评价.研究表明,遗传优化的BP网络模型与未优化的BP网络相比,预测结果更加稳定、误差更小,为工程实际中焊缝缺陷等级评定提供新的方法和依据.

... 2 基于最大似然模糊隶属度估计的磁记忆信号识别由于单一的磁记忆特征参数不能准确地判定焊缝残余应力集中与隐性缺陷的区别,更无法精确定位隐性损伤,因此需要提取多种特征参数进行综合判断^[10],考虑到磁记忆信号的分散性和模糊性,因此从数理统计的角度,融合多种特征参数,引入模糊隶属度函数,采用最大似然估计值进行焊缝残余应力及隐性损伤的精确识别和定位 ...

2016

0.0

... 可能取值的范围,设x₁,x₂,…,x_n为X₁,X₂,…,X_n的一个样本值,样本取到观察值x₁,x₂,…,x_n的概率,即事件{X₁=x₁,X₂=x₂,…,X_n=x_n}发生的概率为^[11]: ...

2008

0.0

... '可作为待估量的估计值^[12] ...

2015

0.0

. 2015, 36(11):1427-1432,1456

Quantitative MMM identification of damage levels based on KNN FSVM for remanufactured sucker rod

基于K-近邻隶属度模糊支持向量机的再造抽油杆损伤等级磁记忆定量识别

Xing Hai-yan , Dang Yong-bin , Wang Ben

邢海燕, 党永斌, 王犇

... 3 正态分布函数概率密度估计在大量试验数据分析基础上,焊缝缺陷的特征值近似符合正态分布^[13] ...

2012

0.0

. 2012, 33(11):2480-2486 DOI:doi:10.3969/j.issn.0254-3087.2012.11.012

Identification of terahertz absorption spectra of explosives based on fuzzy pattern recognition

基于模糊模式识别的爆炸物THz光谱识别

Chen Tao , Li Zhi , Mo Wei.

陈涛, 李智, 莫玮

运用太赫兹(THz)光谱特性对爆炸物进行检测和识别,是现代检测技术研究的一个热点。在对多种单质炸药和混合炸药及几种可能与它们混淆的物质的太赫兹特征吸收光谱进行研究的基础上,提取它们在0.2～2.2THz频率范围内4个相对较强的特征吸收峰作为分类识别的特征参数,用模糊模式识别方法对它们的太赫兹特征吸收谱进行了分类和识别。首先,用基于模糊等价关系的模糊聚类分析方法对这几种物质的太赫兹特征吸收谱进行聚类训练,获得样品分类并形成标准太赫兹吸收光谱模型库;然后,选用与训练样本主体成分相同的2种物品作为待识别对象,采用基于择近原则的模糊模式识别方法进行了成功识别。研究结果表明,基于模糊聚类分析的模糊模式识别方法对太赫兹吸收谱具有较强的相似特征聚类功能和较高的识别率,为太赫兹光谱技术用于爆炸物的检测和识别提供了一种有效的方法。

... 4 模糊隶属度函数模糊模式识别方法是利用模糊数学中的概念、原理及方法解决分类识别问题^{[14,15,16,17]},根据实际问题进行特征提取,建立模糊集的隶属度函数,或建立元素之间的模糊相似关系,并确定这个关系的隶属度函数,然后运用相关的模糊数学的方法进行分类识别 ...

2016

0.0

. 2016, 9(1):41-50 DOI:doi:10.3788/CO.20160901.0041

Review of non-blind deconvolution image restoration based on spatially-varying PSF

空间变化PSF非盲去卷积图像复原法综述

Hao Jian-kun , Huang Wei , Liu Jun

郝建坤, 黄玮, 刘军

传统的图像复原一般认为点扩散函数(PSF)是空间不变的,实际光学系统由于受到像差等因素的影响,并非严格的线性空间不变系统,基于空间变化PSF的非盲去卷积图像复原法逐渐体现其优越性。空间变化PSF的非盲去卷积图像复原法先准确估计图像空间变化的PSF,再利用非盲去卷积算法对图像进行复原,有利于恢复出高质量图像。本文从算法的角度综述了近几年提出的基于空间变化PSF的非盲去卷积图像复原方法,并对比了基于强边缘预测估计PSF的非盲去卷积法、基于模糊噪声图像对PSF估计非盲去卷积法等算法的优缺点,各算法分别在PSF估计精确度、振铃效应抑制效果、适用范围等方面体现出各自的优劣。空间变化PSF的非盲去卷积图像复原法的研究,有利于推进图像复原技术向更高水平发展,使光学系统往轻小型化方向发展,从而在多个科学领域发挥其重要作用。

... 依据试验数据的实际分布规律(见图3),本文采用半梯形隶属度分布函数^[15],正常情况采用偏小型半梯形分布,隐性损伤采用偏大型半梯形分布 ...

2016

0.0

. 2016, 31(12):1161-1167 DOI:doi:10.3788/YJYXS20163112.1161

Real-time color image enhancement method based on FPGA

一种基于FPGA的彩色图像实时增强方法

Hou Tian-jiao , Hao Zhi-cheng , Zhu Ming

侯天娇, 郝志成, 朱明

摘　要：彩色图像中包含了丰富的颜色信息,能够直观地感知世界,它使我们的工作生活更加便利。但是,由于一些恶劣环境的影响,彩色图像的成像会出现模糊、目标被淹没、对比度偏低等问题。针对此问题,本文设计了一款基于FPGA的嵌入式实时图像增强处理系统。并提出一种灰度值拉伸变换方法,将该方法直接对RGB色彩空间的R、G、B三分量进行增强处理,既增大了灰度值的变化范围提高人眼视觉效果,也避免了色彩空间转换带来的计算量及节省了处理时间满足了工程的实时性要求。目前该系统已在实际工程项目中应用,工程结果表明该系统工作稳定有效,能够有效解决工程中出现的光线条件差,低对比度情况下的彩色图像增强问题。

2016

0.0

. 2016, 9(2):226-233 DOI:doi:10.3788/CO.20160902.0226

Super-resolution reconstruction of multiformat laser range-gated image by the estimate of point-spread function

多帧距离选通图像点扩散函数估计的超分辨率重建

Xu Ting-fa , Luo Xuan , Su Chang

许廷发, 罗璇, 苏畅

摘　要：为了解决水下激光距离选通图像成像过程中退化模型复杂的难题,提出了利用连续帧图像估计点扩散函数的距离选通超分辨成像方法。首先,从连续帧图像中选取一帧为参考帧作为初始清晰图像,下一帧图像为模糊图像,用梯度约束的方法求出点扩散函数,用于优化清晰图像;然后,依次将后续帧图像当作模糊图像与清晰图像交替迭代求取点扩散函数并优化更新清晰图像;最后获得的清晰图像与参考帧图像用乘法更新的方法估计点扩散函数,结合凸集投影法算法进行超分辨率成像重建。仿真实验结果表明,改进的算法重建图像分辨率和质量明显优于原始的算法。

2014

0.0

. 2014, 29(2):110-114

Based on trapezoidal fuzzy algorithm to determine the quality of electric energy

基于梯形隶属度模糊算法对电能质量的判断

Liu Liang , Jin Bin , Chu Zhan-ping.

刘亮, 靳斌, 初战平

摘　要：为提高和改善电能质量，以判断某一大中型水务公司电能质量为背景，利用智能电表（FKGA44一ZY200），在对该水厂电能质量数据的采集基础上，针对判断电能质量各项指标间的不确定关系，提出了一种基于梯形隶属度函数模糊算法对电能质量进行综合等级判定的方法。该方法首先将判定电能质量的各项指标做模糊化处理，并建立梯形隶属度函数模型，然后将隶属度划分为五个等级，最后根据待测点的隶属度级，利用贴近度思想判定待测点的等级，进而实现电能质量的综合判定。