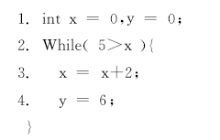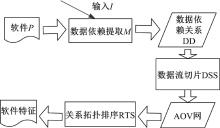
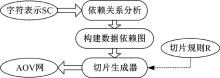
算法基本思想:依据软件算法规定的数据流, 以及数据流之间的依赖关系, 将软件数据流化简序列化, 即为基于数据流切片的软件特征, 流程如图3所示。

首先, 给程序P一定输入I, 获得软件数据

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 软件特征提取过程Fig.3 Extraction process of software feature

流; 其次, 通过软件算法获得数据流之间的依赖关系DD; 再次, 依照数据依赖关系构造数据依赖图, 并通过数据流切片进行依赖图简化; 最后, 进行关系拓扑排序, 将其反序输出作为数据流切片的软件特征。

一个软件的所有数据依赖关系是整个算法的数据流描述, 直接反映了表达式的操作过程和结果, 数据流反应了表达式的数据处理过程。由于表达式的运算中有变量, 而变量参与多个表达式, 变量所携带的数据也参与多个表达式的运算, 造成数据流之间的依赖关系。

随着算法复杂度的增加, 表达式的复杂度和数据量的增大, 数据流依赖关系复杂多样, 对数据依赖的研究也变得复杂。因为数据的依赖关系为单向依赖关系, 而且数据依赖关系有传递性, 所以选择将数据依赖关系抽象成图的形式。数据依赖图将数据流和数据流之间的依赖关系表示出来。具体定义如下。

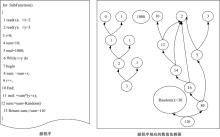
定义6 数据依赖图(Data dependency graph, DDG)。DDG可以表示成G(V, E), V={v_i∈ V|v为软件数据流中的数据}, E={(v_i, v_j)|v_i, v_j∈ V并且v_i=Dep(EXP, v_j)}, 边的单向箭头由v_i 指向v_j, 如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 数据依赖图Fig.4 Data dependency graph

图4给定的源程序, 运行程序并输入x=2, y=3, 跟踪程序运行过程, 记录数据变化, 得到数据流DS={2, 3, 0, 10, 1000, 12, 1, 1, 14, 1, 2, 16, 1, 3, 5, 80, 30, 110}, 即为V, 其中因为数据的产生过程为12=10+2, 1=1+0, 14=12+2, 2=1+1, 16=14+2, 3=2+1, 80=16× 5, 30=Random(), 110=30+80, 所以其中的数据依赖关系依次为12=Dep(sum=sum+x, 10), 12=Dep(sum=sum+x, 2), 1=Dep(i++, 0), 1=Dep(i++, 1), …, 110=Dep(sum=sum+Random(), 80), 110=Dep(sum=sum+Random(), 30)。将得到的数据依赖关系形成数据对E={(12, 10), (12, 2), (1, 0), (1, 1), …, (110, 30), (110, 80)}即为边集合, 使用E和V构成图形DDG。

由数据定义的独立性表明, 数据不可能被重复定义, 则说明数据依赖图为有向无环图。

分析数据流, 获得数据依赖关系, 同时由于软件的一般特征和数据的等价语义变换导致一部分数据流特征不能代表软件。因而需要对得到的数据依赖关系进行相应切片处理。

定义7 数据切片(Data stream slicing, DSS)对程序P一定的输入I, 根据程序P指令的控制, 将获得的程序数据流划分成为一系列的子集, 可以用DS(P, I, r)表示。I表示程序P的输入, r表示数据流切片规则。

数据流切片的规则定义如下:

规则1 由于算法的输出性质, 导致软件至少有一个输出, 软件所有的指令对数据的操作都围绕着输出的数据(返回值或传出值)展开, 所以将与输出数据无依赖关系的数据去除。在DDG中表现为:将DDG看成无向图, 将包含输出数据的最大连通子图留下, 其余子图删除。

规则2 由于算法有可能需要随机数据参与输出数据的运算, 随机数据因为数据不确定, 及对它有依赖关系的数据也不确定, 不能用来表示软件特征。在DDG中表现为:将随机数据节点及其对随机数可达节点都删除。规则2用到的随机数定义如下。

定义8 随机数。设P输入为I, EXP为表达式, d为数据, 且d=Def(EXP), 若在输入I的情况下, 软件P在运行n次中, 产生的d数据为d₁, d₂, …, d_n, 若d_i≠ d_j则称d为随机数。

规则3 由于程序的静态数据的确定性, 不随输入数据而变换, 软件攻击方法可以将静态数据和指令结合, 进行相应整体调整, 造成获得的数据流之间的差异, 所以要去除数据依赖图中的静态数据节点。

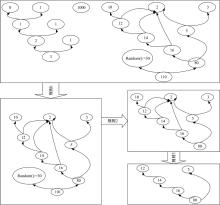
如在图5中将数据依赖图按照规则1, 规则2和规则3处理, 形成依赖图的最简形式图5中第四幅图形, 其中利用规则1, 将原图看成无向图, 将不包含110节点的连同子图去除; 利用规则2, 将Random():=30节点及其可以到达的110节点去除; 利用规则3将静态数据去除, 得到最终的数据依赖子图。

将数据依赖图序列化, 将有利于软件特征的相似度计算。为了进一步研究, 使用顶点活动网(Activity on vertex network, AOV), 将AOV网拓扑排序算法对数据依赖图进行序列化。在依赖图的AOV网中DDG的v_i=Dep(Exp, v_j), 可称v_i 为v_j 的前驱或称v_j 为v_i的后继。相关定义如下:

定义9 偏序关系, 设R是非空集合A上的一个二元关系, 若R满足:

(1)自反性(Reflexive):对任意的a∈ A, (a, a)∈ P;

(2)反对称性(Anti-symmetric):设a∈ A且b∈ A, 若(a, b)∈ R, 且(b, a)∈ P, 则a=b;

(3)传递性(Transitive):设a∈ A且b∈ A, 若(a, b)∈ R, (b, c)∈ P, 则(a, c)∈ P;

则称 R为A上的偏序关系。

定义10 全序关系。如果对每个a, b∈ A, 必有aRb或bRa, 则称R是集合A上的全序(关系)。

定义11 拓扑排序。由某一集合上的一个偏序关系得到该集合上的一个全序关系, 操作过程称为拓扑排序。

定义12 全拓扑排序算法。一个有向图的拓扑排序序列未必唯一, 求得有向图的所有排序的过程为全拓扑排序。

传统AOV网算法都采用栈结构存储, AOV网拓扑排序的算法思想为:

(1)若栈非空, 将入度为0的栈顶节点输出, 若栈空, 则退出程序, 完成算法。

(2)在图中删除该节点, 并删除以该顶点为尾的弧, 并将此节点的前继节点入度减1。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 切片规则举例Fig.5 Example of slice rules

(3)判断是否产生入度为0的节点, 若有则节点入栈, 然后返回继续循环。

在以上3步循环执行中, 依次输出的节点序列称为AOV网的拓扑序列。

在数据依赖图的AOV网研究中, 注重数据之间的依赖关系, 在AOV网传统拓扑排序算法基础之上使用一种新的基于数据依赖关系的拓扑排序算法。

关系拓扑排序算法思想, 利用递归将没有直接或间接数据依赖关系的节点使用集合表示, 将有直接或间接数据依赖关系的节点利用向量表示, 向量顺序表示了节点的先后顺序。算法具体描述如下:

(1)若拓扑图栈非空, 入度为0的节点个数为1, 则跳到第3步; 若个数大于1, 将节点构成集合, 跳到第2步。若个数为0, 退出算法。

(2)若集合元素为1, 则直接输出节点, 若节点元素大于1, 输出“ {” (集合开始符号), 使用集合中每个节点, 通过执行第3步构造集合元素, 最后输出“ }” (集合结束符号)。

(3)若节点有前继节点, 将此节点和前继节点的集合构成向量, 输出“ < ” (开始符号)和此节点, 则将此集合作为输入执行第2步, 输出“ > ” (向量结束符号)。若节点没有后继节点, 输出此节点。

经过以上3步计算操作, AOV网将形成关系拓扑排序。可分为两种:①字符串向量中的元素之间依照前后之间顺序及依赖关系; ②字符串集合中的元素无元素依赖关系, 如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 关系拓扑排序举例Fig.6 Example of relationship topological sort

图6为依照数据依赖图的化简后的最简形式, 然后进行的关系拓扑排序。集合关系表示了元素的无序关系, 向量表示了元素的序列关系。80=Dep(mul:=sum× (y+x), 5)和80=Dep(mul:=sum× (y+x), 16), 80必须在16和5之前用向量表示; 5与16没有依赖关系, 使用集合表示; 16, 14和12有相互依赖关系, 使用向量表示(16, 14, 2)。

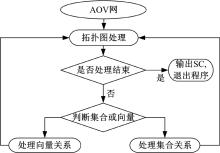
根据数据流软件特征提取算法要求, 设计软件特征系统包括:特征提取模块(数据依赖提取、数据依赖切片和拓扑排序)、数据收集模块和相似度比较模块3个部分, 如图7和图8所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 软件特征系统模型Fig.7 Software features system model

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 系统实现过程Fig.8 Realization process of system

从图8可以看到:首先将 P0(程序源码)送入特征提取模块, 并有输入 I,由SFDS得到数据流特征字符串SC; 将 P1(程序可执行文件)送入数据收集D, 并有一定的输入I, 得到数据字符串DS。再将SC与DS输入相似度比较模块Similarity, 最后得到数据流切片特征相似度报告。

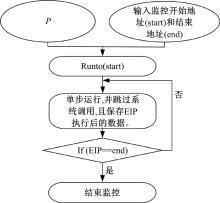
依照基于数据流切片的软件特征提取算法的原理, SFDS模块运行过程如下:将P₀ 送到调试监控模块M, 根据输入I使得P₀监控运行, 并得到程序运行中间数据及数据依赖关系。然后数据切割DSS依据切片规则 r对得到的数据和数据依赖关系进行选择切片, 得到AOV网, 最后进行拓扑排序RTS, 得到软件特征字符串表示SC。

数据切片DSS主要负责将从调试监控得到的数据依赖关系转化为AOV网。DSS首先获得数据依赖关系, 其次进行数据依赖关系分析, 再次依据2.2节的数据依赖图构造方法构造数据依赖图。最后依据2.3节介绍的3条切片规则, 逐一对数据流图进行切割, 得到化简的AOV网。DDS工作流程如图9所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 数据流切片流程Fig.9 Process of data flow slicing

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 拓扑排序RTS模块工作流程Fig.10 Flow chart of topological sort RTS module

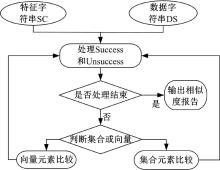
拓扑排序RTS主要负责将得到的AOV网进行关系排序。根据2.4节描述的关系拓扑排序算法设计程序流程实现时, 将处理向量关系和处理集合关系分别变成函数, 将形成一个递归的处理模式, 直到AOV网元素逐个处理结束, 流程如图10所示。

将 P1在IDA环境中加载运行, 开发IDC脚本文件控制IDA使得 P1单步调试运行, 并记录每条汇编语言执行后, 记录EAX、EBA、ECX、EDX、ESI、EDI、ESP、EBP、EIP的数值, 及其对应的有效的内存地址的值, 并将其按顺序排列生成数据字符串DS。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 数据收集模块流程Fig.11 Flow chart of data collection module

在IDA中加载完IDC文件后, 输入程序 P和P中需要监控的起始位置start和结束位置end; 然后, P运行到start位置开始监控, 跳过系统调用, 单步运行每一条反汇编语句, 并记录数据包括EAX、EBX、ECX、EDX、ESI、EDI、ESP、EBP、EIP的数值, 及其对应的有效的内存地址的值; 最后判断是否运行到end, 如果是则结束监控, 否则循环到单步运行处继续执行, 数据收集如图11所示。

相似度比较模块主要负责将得到的数据流特征字符串SC和数据字符串DS进行比较。根据3.4节描述的数据收集和加载过程设计程序流程, 向量元素比较和集合元素比较分别形成一个递归的处理模式, 直到字符串比较完毕。比较流程如图12所示。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 相似度比较模块工作流程Fig.12 Flow chart of similarity comparison module

由于基于数据流切片的软件特征提取算法是在数据流基础之上做的软件特征研究, 所以算法对软件有以下两点要求:

(1)软件运行中有数据流产生。不同的运算符号, 使得变量数据改变, 而产生新数据。以下基于C语言列出通用产生数据的计算符, 包括运算符号和赋值运算。

(a)常用的运算符分为3大类:算术运算符、关系运算符、逻辑运算符。各种算术运算对数据流影响见表1所示。

(b)赋值语句形式为:< 变量> =< 表达式> ; 利用“ =” 将表达式的值赋给左边变量, 造成新的数据流, 即便是变量赋值前后数值大小一样, 依然是两个不同的数据。

(2)数据流长度要达到一定要求, 具体数据量将根据应用软件的不同而不同。当数据流数量达到一定程度时, 数据流切片的特征唯一性更高。

表1

Table 1

表1(Table 1)

表1 运算符对数据流影响 Table 1 Operator's influence on data flow 算术运算符 关系运算符 逻辑运算符 运算符 运算 产生新数据流 运算符 运算 产生新数据流 运算符 运算 产生新数据流 + 正号 否 < 小于 是 & & 与 是 - 负号 否 < = 小于等于 是 || 或 是 + 加 是 > 大于 是 ! 非 是 - 减 是 > = 大于等于 是 * 乘法 是 == 等于 是 / 除法 是 != 不等于 是 % 取模 是

表1 运算符对数据流影响 Table 1 Operator's influence on data flow

本实验选择快速排序(Quick sort, QS)和冒泡排序(Bubble sort, BS)程序作为实验对象。为了使实验更具客观性且便于观察, 限定QS和BS输入同都为 I, I元素有3部分组成1AB:A由两位组成, 从01到50, 表示数字的百位和千位; B由两位组成, 从01到50, 表示数字个位与十位; 1、A和B共同组成5位数字, 并以此按从小到大顺序排列。由于要求特征字符串长度尽可能的长, 所以将数据按照快速排序交换次数最多的情况来安排输入数据I, 如图13所示。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 QS和BS输入数据Fig.13 Input data of QS and BS

鲁棒性实验过程分为两部分, 以快速排序QS为例分别如下:

(1)在输入 I的情况下, 计算QS的数据流切片的软件特征QS_SFDS; 再次, 通过数据收集模块 D收集QS运行数据QS_DS; 最后, 通过QS_SFDS和QS_DS计算软件相似度值, 即Similarity(QS_SFDS, QS_DS)。

(2)在输入 I情况下, 分别计算QS的数据流切片的软件特征QS_SFDS; 再次, 将QS可执行程序经过混淆形成QS', 将QS'通过数据收集模块D收集QS'运行数据QS'_DS; 最后, 通过QS_SFDS和QS'_DS计算软件相似度值, 即Similarity(QS_SFDS, QS'_DS)。

经过对数据严格操作, 周密安排实验, 得到实验报告和分析如表2所示。

从表2中看出, 测得的相似性都比较高。

表2

Table 2

表2(Table 2)

表2 鲁棒性实验 Table 2 Robustness experiment 输入 SFDS DS 相似度/% 特征程序 元素个数/个 来源 大小/K I QSSFDS 313 QSDS 735 Similarity(QSSFDS, QSDS)=100.00 QSSFDS 313 QS'DS 15722 Similarity(QSSFDS, QS'DS)=99.85 I BSSFDS 6222 BSDS 949 Similarity(BSSFDS, BSDS)=99.48 BSSFDS 6222 BS'DS 74712 Similarity(BSSFDS, BS'DS)=99.93

表2 鲁棒性实验 Table 2 Robustness experiment

Similarity(QS_SFDS, QS_DS)和Similarity(BS_SFDS, BS_DS), 因为SFDS是在软件调试运行中获得数据及其依赖图简化而来的, 而DS为算法整个数流的集合, 所以SFDS为DS的子集。Similarity(QS_SFDS, QS'_DS)与Similarity(BS_SFDS, BS'_DS)是对软件进行混淆后软件基于数据流切片的软件特征依然可以完整的提取, 实验验证了基于数据流切片的软件特征提取不管是部分提取, 还是混淆攻击后提取, 特征相似度仍保持较高, 说明算法具有良好的鲁棒性。

实验步骤如下:首先, 在C++控制台应用程序编写经典的快速排序算法(QS)和冒泡排序算法(BS); 其次, 在输入I的情况下, 分别计算QS和BS的数据流切片的软件特征QS_SFDS和BS_SFDS; 再次, 在输入I的情况下, 获得收集QS_DS和BS_DS运行数据信息; 最后计算Similarity(QS, BS)和Similarity(BS, QS)。

表3

Table 3

表3(Table 3)

表3 置信度实验 Table 3 Confidence experiment % X Y QSDS BSDS QSSFDS 100 52.8435 BSSFDS 3.6382 100

表3 置信度实验 Table 3 Confidence experiment %

由实验结果可知, Similarity(QS_SFDS, BS_DS)为52.8435%, 而Similarity(BS_SFDS, QS_DS)为3.6382%, 两者都不可能接近90%, 说明软件的不同, 相似度差异较大。由于SFDS与程序输入和算法有关, 而QS与BS同为排序算法, 并且输入同为I, 又由于BS对于数据进行两次循环, 相当于数据全排列, 所以包含数据I的全部排列情况, 因而Similarity(QS_SFDS, BS_DS)相似比较高, 但随着SFDS字符串的变长, 其相似性不断变小, 因些当提取足够的特征切片时, 不会影响到软件识别。