机械零部件动态可靠性稳健优化设计的群智能算法

引用本文

于繁华, 刘仁云, 张义民, 张晓丽, 孙秋成. 机械零部件动态可靠性稳健优化设计的群智能算法[J].吉林大学学报（工学版）, 2017,47(6): 1903-1908
YU Fan-hua, LIU Ren-yun, ZHANG Yi-min, ZHANG Xiao-li, SUN Qiu-cheng. Swarm intelligence algorithm of dynamic reliability-based robust optimization design of mechanic components[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1903-1908 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706031
Permissions

机械零部件动态可靠性稳健优化设计的群智能算法

于繁华¹, 刘仁云², 张义民³, 张晓丽^1,³, 孙秋成¹

1.长春师范大学计算机科学与技术学院,长春 130032

2.长春师范大学数学学院,长春 130032

3.东北大学机械工程与自动化学院,沈阳 110004

通讯作者：刘仁云(1968-),女,教授,博士.研究方向:计算智能,结构可靠性设计与优化.E-mail:liurenyun2005@163.com

作者简介:于繁华(1970-),男,教授,博士.研究方向:计算智能及应用.E-mail:yufanhua@163.com

基金:吉林省产业创新专项资金项目(2017C031-2); 吉林省教育厅项目(吉教科合字[2014]第17号、吉教科合[2013]第243号)

摘要

在运用随机过程和顺序统计原理建立载荷和强度随时间变化的动态可靠性模型基础上,利用稳健设计理论,建立了机械零部件动态可靠性稳健优化设计的多目标优化模型。针对该多目标模型所具有的动态高维的特点,提出了基于灰色关联分析的多粒子群协同动态多目标优化算法。以钢板弹簧结构为例,给出了动态环境下随时间变化的最优解集,为机械零部件的动态可靠性稳健优化设计提供了理论依据。

关键词: 计算机应用; 极端学习机; 动态粒子群算法; 可靠性优化设计; 多目标优化

中图分类号:TP39;TH12 文献标志码:A 文章编号:1671-5497(2017)06-1903-06

Swarm intelligence algorithm of dynamic reliability-based robust optimization design of mechanic components

YU Fan-hua¹, LIU Ren-yun², ZHANG Yi-min³, ZHANG Xiao-li^1,³, SUN Qiu-cheng¹

1.College of Computer Science & Technology, Changchun Normal University, Changchun 130032, China

2.College of Mathematics, Changchun Normal University, Changchun 130032, China

3.College of Mechanical Engineering and Automation, Northeastern University, Shenyang 110004, China

Abstract

A dynamic reliability-based model, whose load and strength vary with time, is established by using random process and order statistics theory. Then, applying robust optimization design theory, a multi-objective optimization model is proposed for the dynamic reliability-based robust design of mechanic components. Considering the dynamic high-dimensional characteristics of the proposed model, a multiple particle swarm co-evolutionary algorithm based on grey correlation analysis theory is developed for the multi-objective optimization. The leaf-spring is taken as an example for solving the optimal solution set in dynamic environment. Results demonstrate that the proposed method can provide theoretical foundation for dynamic reliability-based robust design of mechanic components.

Keyword: computer application; extreme learning machine; dynamic particle swarm algorithm; reliability optimization design; multi-objective optimization

Show Figures

0 引言

在机械产品的设计中如果不考虑动态特性将难以得到准确的失效数据和可靠性信息, 进而制约了机械产品的设计水平。近年来, 关于机械零部件动态可靠性的研究已成为热点问题^{[1, 2, 3]}。研究者运用概率密度演化、顺序统计理论、随机摄动技术、支持向量机等方法进行了动态可靠性的研究, 为动态可靠性研究提供了良好的基础^{[4, 5, 6, 7]}。机械零部件可靠性稳健设计要求在进行结构设计时可靠度对设计参数的变化不敏感, 为满足这一要求, 需要建立机械零部件可靠性稳健优化设计多目标模型。在该领域通常将多目标问题转化为单目标问题来处理, 由于问题的复杂性很难得到令人满意的结果。国内外学者们运用遗传算法和群智能算法来解决可靠性稳健优化多目标设计模型的求解问题^{[8, 9, 10, 11]}。然而, 上述算法所求得到优化设计解是机械零部件在静止环境下的最优解, 对于时间域上的动态可靠性稳健优化设计尚不能直接应用。同时, 由于可靠性稳健设计模型多为高维多目标优化问题, 静态高维多目标优化中存在的求解困难问题也会被动态高维多目标优化所继承。

针对这种情况, 本文在建立机械动态可靠性稳健设计高维动态多目标模型的基础上, 将动态优化策略与高维多目标求解方法相结合, 提出了基于灰色关联分析的多粒子群协同动态多目标优化算法, 以此来解决动态可靠性稳健设计的高维多目标模型的求解难题。这项工作不仅对机械动态可靠性稳健优化设计具有重要意义, 同时也将对多目标优化领域的研究起到积极的推动作用。

1 动态可靠性稳健优化设计模型

由于机械零部件在使用期间将受到外界条件和材料自身因素的影响, 其强度逐渐退化和随机载荷变化是不能被忽视的, 必须引入时间概念用随机过程来描述强度和载荷的变化历程。根据应力-强度干涉理论, 其极限状态方程表示为:

$\begin{matrix} g (t) = r (t) - σ (t) (1) \end{matrix}$

式中: $\begin{matrix} g (t) \end{matrix}$ 为零部件结构的功能函数; $\begin{matrix} r (t) \end{matrix}$ 为零部件强度退化的随机过程; $\begin{matrix} σ (t) \end{matrix}$ 为载荷作用效应随机过程。

文献[2]在研究机械零部件载荷、强度和可靠度随时间变化规律的基础上, 运用随机过程和顺序统计原理建立了载荷和强度随时间变化的动态可靠性模型, 采用二阶矩和随机摄动方法进行机械零部件的动态可靠性指标和动态可靠度计算。本文将采用该方法求出动态可靠性指标, 并计算出零部件的动态可靠度。

针对机械零部件动态可靠性稳健优化设计问题, 一般需要开展如下工作:

(1)要求每个时间段下零部件费用(体积、质量等)最小;

(2)要求可靠度对设计参数的变化不敏感;

(3)要求零部件在服役期的任意时间段可靠性指标都大于给定可靠性指标;

(4)要求给出每个时间段符合上述3个条件的最优设计参数。

基于上述情况, 建立的动态高维多目标可靠性稳健优化设计模型为:

$\begin{matrix} \{\begin{matrix} \min f_{1} (X) \\ \min f_{i} (X) = |\frac{\partial R (t)}{\partial X}| \\ s . t . β (t) \geq β_{T} \end{matrix} (2) \end{matrix}$

式中:目标函数f₁(X)为体积、质量等问题, X为设计变量; R(t)为某个时间段下的可靠度; f_i (X)(i=1, 2, …, n)为可靠度对设计变量的灵敏度; β _T为给定的可靠性指标。

2 基于灰色关联分析的多粒子群协同动态多目标优化算法

2.1 灰色关联分析

在灰色系统中比较事物、因素之间的动态发展相似程度是通过计算灰色关联度来实现的, 即灰色关联度值越大, 说明事物之间的相似程度就越高, 否则就越低^[12]。

假设基准矢量序列Y₀={y₀ (i), i=1, 2, …, n}, 目标矢量序列Y_j={y_j (i), i=1, 2, …, n; j=1, 2, …, m}, 这里n为每个矢量的项数, m为目标矢量的个数。则Y_j对于 $\begin{matrix} Y_{0} \end{matrix}$ 在第 $\begin{matrix} k \end{matrix}$ 点的灰色关联系数为:

$\begin{matrix} \begin{matrix} ε_{0 j} (k) = (\min_{j} \min_{i} | y_{0} (i) - y_{j} (i) | + \\ δ \max_{j} \max_{i} | y_{0} (i) - y_{j} (i) |) / \\ (| y_{0} (i) - y_{j} (i) | + δ \max_{j} \max_{i} | y_{0} (i) - y_{j} (i) |) (3) \end{matrix} \end{matrix}$

关联度为:

$\begin{matrix} γ = \frac{1}{n} \overset{n}{\sum_{i = 1}} ε_{0 j} (i) (4) \end{matrix}$

式中:δ 为分辨系数, 通常取值为0.5, 当δ =0时, 环境消失; 当δ =1时, 环境原封不动地保持。

2.2 基于灰色关联分析的多种群协同优化策略

如果有M个优化目标(函数)则产生M个种群, 第i个种群对应第i个优化目标f^i, 每个种群的粒子数目为N。第i个种群在每次迭代时从N个粒子中选取所对应目标fⁱ适应度最高的粒子, 将其作为该种群的群内极值, 记为 $\begin{matrix} p_{g}^{i} 。 \end{matrix}$

把每个种群适应度最高的粒子代入各自目标函数中, 记为 $\begin{matrix} f^{1} (X_{j}^{1}), f^{2} (X_{j}^{2}), \dots, f^{M} (X_{j}^{M}), \end{matrix}$ 该序列作为当前迭代最满意的基准矢量。把 $\begin{matrix} M \end{matrix}$ 个种群中的所有粒子都分别代入到目标函数中, 形成 $\begin{matrix} M \times N \end{matrix}$ 个目标矢量, 记为:

$\begin{matrix} \{\begin{matrix} f^{1} (X_{1}^{1}), f^{2} (X_{1}^{1}), \dots f^{M} (X_{1}^{1}) \\ ︙ \\ f^{1} (X_{N}^{1}), f^{2} (X_{N}^{1}), \dots f^{M} (X_{N}^{1}) \\ f^{1} (X_{1}^{M}), f^{2} (X_{1}^{M}), \dots f^{M} (X_{1}^{M}) \\ ︙ \\ f^{1} (X_{N}^{M}), f^{2} (X_{N}^{M}), \dots f^{M} (X_{N}^{M}) \end{matrix} (5) \end{matrix}$

式中: $\begin{matrix} j = 1, 2, \dots, N; i = 1, 2, \dots, M 。 \end{matrix}$

通过式(4)计算这 $\begin{matrix} M \times N \end{matrix}$ 个目标矢量, 灰色关联度值最大的那个矢量的粒子作为全局极值, 记为 $p_{g}^{s}$ , 该全局极值被M个种群所共享。基于此, 将基本粒子群算法公式修改为:

$V_{j}^{i} (q + 1) = W V_{j}^{i} + C_{1} r_{1} (P_{g}^{i} (q) - X_{j}^{i} (q)) + C_{2} r_{2} (P_{g}^{s} (q) - X_{j}^{i} (q)) (6)$

$X_{j}^{i} (q + 1) = X_{j}^{i} (q) + V_{j}^{i} (q + 1) (7)$

式中: $V_{j}^{i} (q)$ 为第i个种群第j个粒子在第q次迭代的速度; $X_{j}^{i} (q)$ 为第i个种群第j个粒子在第q次迭代的位置; $\begin{matrix} C_{1} \end{matrix}$ 和 $\begin{matrix} C_{2} \end{matrix}$ 为学习因子; $\begin{matrix} W \end{matrix}$ 为惯性因子; $\begin{matrix} r_{1} \end{matrix}$ 和 $\begin{matrix} r_{2} \end{matrix}$ 为随机数, 其取值为(0, 1)。

上述计算过程的思想是在社会学习过程中某个种群成员都要向该种群中认知能力最强的个体学习, 只有这样, 种群的所有成员才会向最优方向移动; 由于单个种群只能从所对应的目标获取知识, 存在认知片面性, 难以获得整个社会(全部种群)的知识, 所以需要采用一种有效的规则在全种群中遴选认知能力相对全面同时也相对丰富的榜样, 让全种群的粒子都向榜样学习, 以此来促进全种群成员认知能力提升, 并相互促进、相互进步, 这是把基本粒子群算法单目标优化的思想拓广到多目标优化领域。同时, 从算法的实施方式来看, 它特别适合高维多目标优化问题的求解, 是一种非pareto优化求解算法, 避免了目标维数增大所带来的维数灾难问题。

2.3 环境变化的自检算子

动态优化问题的关键是在环境发生改变时, 如何使算法自动跟踪环境的变化而继续寻找新的最优解。对粒子群算法中的个体粒子来说, 环境发生变化后个体粒子所对应的适应度值也会发生相应变化。如果出现前、后代粒子的位置接近而对应适应度值却显著不同, 基本上可以推断环境发生了变化^[13]。在多种群情况下, 每个种群中的群内极值 $\begin{matrix} P_{g}^{i} \end{matrix}$ 对环境变化最为敏感, 所以将其设为检测环境变化的哨兵, 令哨兵粒子前、后代适应度值与其所对应距离的比值为:

$H^{i} (q) = \frac{f^{i} (p_{g}^{i} (q)) - f^{i} (p_{g}^{i} (q - 1))}{S^{i} (q)} (8)$

$\begin{matrix} \begin{matrix} S^{i} (q) = \sqrt[]{(p_{g}^{i} (q) - p_{g}^{i} {(q - 1))}^{2}} (9) \end{matrix} \end{matrix}$

式中: $\begin{matrix} q \end{matrix}$ 为粒子迭代数; $\begin{matrix} H^{i} (q) \end{matrix}$ 为哨兵粒子前、后代适应度值变化与距离变化的比值。

哨兵粒子前、后代适应度值与距离比值的变化率为:

$\begin{matrix} C^{i} (q) = \frac{H^{i} (q)}{H^{i} (q - 1)} (10) \end{matrix}$

式中:当环境没有发生变化时, $\begin{matrix} C^{i} (q) \end{matrix}$ 的值接近1, 当环境发生变化时其值将产生跃变。

2.4 响应环境变化策略

当环境变化时需要对各种群粒子重新设置初始值, 产生初始值的原则是:①由于材料强度和可靠度随时间推移会呈现逐渐下降趋势, 最近时间段内所得到的最优解可能是最接近下一个时间段的最优解, 为了加快算法的收敛速度, 利用式(11)在全局极值附近选取50%的粒子作为初始值; ②为加强解的多样性, 使其能够更好地搜索到全局最优解, 剩下50%粒子将随机产生。

$\begin{matrix} X_{j}^{i} = P_{g}^{s} + rand {(- 1, 1)}^{D} \times ρ (11) \end{matrix}$

式中: $\begin{matrix} D \end{matrix}$ 为解的维度, 即设计参数的个数; rand()为产生服从正态分布的 $\begin{matrix} D \end{matrix}$ 维矢量; $\begin{matrix} ρ \end{matrix}$ 为给定的常量, 根据每个设计参数的取值范围给出。

2.5 算法描述

Step1 初始化每个种群:粒子位置 $\begin{matrix} X_{j}^{i} 、 \end{matrix}$ 粒子的飞行速度 $\begin{matrix} V_{j}^{i} 、 c_{1} 、 c_{2} 、 w \end{matrix}$ 的值、最大迭代次数T_max、给定适应度阈值 $\begin{matrix} η \end{matrix}$ 以及种群规模N。

Step2 在每个种群内计算各粒子适应度值, 选取群内极值 $\begin{matrix} P_{g}^{i}, \end{matrix}$ 利用式(3)(4)给出全局极值 $\begin{matrix} P_{g}^{s} \end{matrix}$ 。

Step3 利用环境变化的自检算子, 判断环境是否发生变化, 若变化执行响应环境变化策略; 否则执行下一步。

Step4 while(适应度值> $\begin{matrix} η \end{matrix}$ & & 迭代次数< T_max)

{

执行式(6)(7)

计算适应度函数;

选取群内极值 $\begin{matrix} P_{g}^{i} \end{matrix}$ ;

利用式(3)(4)给出全局极值 $\begin{matrix} P_{g}^{s} \end{matrix}$ ;

}

输出本时间段内的最优解

Goto Step3

Step5 结束

3 钢板弹簧的动态可靠性稳健优化设计

3.1 力学模型

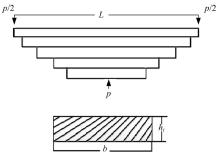
在实际工程中车辆钢板弹簧一般都是中心受载的简支叠板弹簧, 按照固定的宽度把其截开重叠使用, 如图1所示。通常采用应力梁计算公式对钢板弹簧垂直方向载荷进行计算, 其工作应力的计算公式为:

$\begin{matrix} σ_{i} = \frac{3 pL}{2 b} \frac{h_{i}}{n_{1} h_{1}^{3} + n_{2} h_{2}^{3} + \dots + n_{m} h_{m}^{3}} (12) \end{matrix}$

	Figure Option View Download New Window
	图1 钢板弹簧Fig.1 Leaf spring

最厚板的最大应力为:

$\begin{matrix} σ_{\max} = \frac{3 pL}{2 b} \frac{h_{\max}}{n_{1} h_{1}^{3} + n_{2} h_{2}^{3} + \dots + n_{m} h_{m}^{3}} (13) \end{matrix}$

式中: $\begin{matrix} p \end{matrix}$ 为载荷; $\begin{matrix} b \end{matrix}$ 为宽度; $\begin{matrix} h_{i} \end{matrix}$ 为厚度; $\begin{matrix} L \end{matrix}$ 为跨距; $\begin{matrix} n_{i} \end{matrix}$ 为钢板片数。

为避免计算的复杂性, 在此忽略叠板之间摩擦对工作应力的影响, 在实际应用中这种近似的方法是允许的。

利用文献[2]提出的方法计算钢板弹簧的动态可靠性指标 $\begin{matrix} β (t) \end{matrix}$ 和动态可靠度 $\begin{matrix} R (t) 。 \end{matrix}$

3.2 汽车钢板弹簧的动态可靠性稳健优化设计

国产某型汽车钢板弹簧的片数n₁=2, n₂=6, n₃=4; 载荷p为(μ _p, σ _p) =(16503.2, 825.16) N, 钢板弹簧的跨距 $\begin{matrix} L 为 (μ_{L}, σ_{L}) \end{matrix}$ =(1475, 7.375) mm; 材料强度r为(μ _r, σ _r) =(614, 45.8) MPa。给定的可靠度指标为 $\begin{matrix} β \geq 3, \end{matrix}$ 设计使用期为5000 h。利用文中提出的动态可靠性稳健优化设计方法, 计算出此多片不同厚度钢板弹簧的最小厚度h₁、h₂ 、h₃ 和最小宽度b。

(1)动态可靠性稳健优化设计多目标函数的建立。由于要求钢板弹簧的质量最小, 所以要求截面面积为最小:

$\begin{matrix} f_{1} (X) = x_{1} (n_{1} x_{2} + n_{2} x_{3} + n_{3} x_{4}) (14) \end{matrix}$

取设计变量为:X=(x₁, x₂, x₃, x₄ )^T=(b, h₁, h₂, h₃ )^T, 其中b、h₁、h₂、h₃为钢板弹簧的几何尺寸。

由于要求可靠度对设计参数的变化不敏感, 所以需要钢板弹簧的可靠度对设计变量 $\begin{matrix} X = (x_{1}, x_{2}, x_{3}, x_{4})^{T} \end{matrix}$ 均值的灵敏度为最小。

$\begin{matrix} \{\begin{matrix} f_{2} (X) = \frac{\partial R (t)}{\partial x_{1}} \\ f_{3} (X) = \frac{\partial R (t)}{\partial x_{2}} \\ f_{4} (X) = \frac{\partial R (t)}{\partial x_{3}} \\ f_{5} (X) = \frac{\partial R (t)}{\partial x_{4}} \end{matrix} (15) \end{matrix}$

(2) $\begin{matrix} β (t) \geq 3, x_{2} - x_{3} \geq 1.0, x_{3} - x_{4} \geq 1.0 \end{matrix}$ 为约束条件。

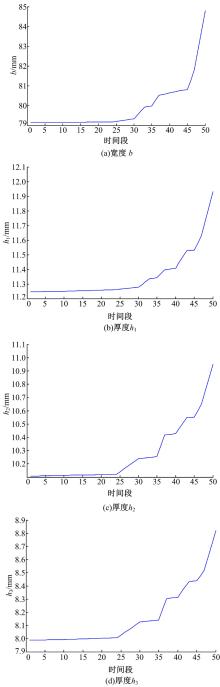
(3)动态高维多目标优化求解。根据优化目标函数的要求生成5个种群, 在每个种群中随机产生50个粒子的位置 $\begin{matrix} X_{j}^{i} \end{matrix}$ 和速度 $\begin{matrix} V_{j}^{i}; \end{matrix}$ 设定学习因子为 $\begin{matrix} c_{1} = c_{2} = 1.2; 惯性因子 w \end{matrix}$ 从1.2递减到0.2; 每个种群最大迭代次数为100次。将设计基准期分为50个相等的时间段, 利用2.5节所介绍的方法, 计算出每个时间段下最优的设计参数, 结果如图2所示。

从图2可以看出:最优设计尺寸在部件服务初期以及中期都比较平稳, 没有发生大的改变, 而到中后期由于零部件强度随时间逐渐减弱, 最优尺寸呈上升趋势, 以此来保证部件可靠性指标的要求。这也说明可靠性随着时间的推移呈现递减的趋势。同时, 设计者可以依据服役期和可靠度的要求, 通过该模型选择最佳的设计尺寸。

	Figure Option View Download New Window
	图2 钢板弹簧几何尺寸随时间变化曲线Fig.2 Curves of geometric size of spring plate changes over time

4 结论

(1)建立了随时间变化的动态可靠性稳健设计多目标优化模型, 由于所建立的模型多为动态高维多目标问题, 给出了适合该问题求解的灰色关联分析多粒子群协同动态多目标优化算法。

(2)在机械零部件的动态可靠性稳健优化设计过程中, 设计者只需给出零部件的服役期以及要求达到的可靠度指标, 便可以通过本文方法找到相应的优化设计尺寸, 为工程设计人员精确设计零部件提供定量的依据, 为零部件的制造、使用和评估提供技术支持。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张义民. 机械动态与渐变可靠性理论与技术评述[J]. 机械工程学报, 2013, 49(20): 101-114. Zhang Yi-min. Review of theory and technology of mechanical reliability for dynamic and gradual systems[J]. Journal of mechanical Engineering, 2013, 49(20): 101-114. [本文引用:1]
[2]	王新刚, 张义民, 王宝艳. 机械零部件的动态可靠性灵敏度分析[J]. 机械工程学报, 2010, 46(10): 188-193. Wang Xin-gang, Zhang Yi-min, Wang Bao-yan. Dynamic reliability sensitivity analysis of mechanical components[J]. Journal of Mechanical Engineering, 2010, 46(10): 188-193. [本文引用:1]
[3]	王正, 康锐, 谢里阳. 以载荷作用次数为寿命指标的失效相关系统可靠性建模[J]. 机械工程学报, 2010, 46(3): 188-197. Wang Zheng, Kang Rui, Xie Li-yang. Reliability modeling of systems with dependent failure when the life measured by the number of loadings[J]. Journal of Mechanical Engineering, 2010, 46(3): 188-197. [本文引用:1]
[4]	刘仁云, 侯树范, 张义民. 基于多目标优化策略的螺旋弹簧可靠性稳健优化设计[J]. 机械强度, 2012, 34(2): 214-218. Liu Ren-yun, Hou Shu-fan, Zhang Yi-min. Robust optimization design for reliability for coil spring based on multi-objective decision making methods[J]. Journal of Mechanical, 2012, 34(2): 214-218. [本文引用:1]
[5]	Li J, Chen J B, Fan W L. The equivalent extreme-value event and evaluation of the structural system reliability[J]. Structural Safety, 2007, 29(2): 112-131. [本文引用:1]
[6]	韩彦彬, 白广忱, 李晓颖, 等. 基于支持向量机柔性机构动态可靠性分析[J]. 机械工程学报, 2014, 50(11): 86-92. Han Yan-bin, Bai Guang-chen, Li Xiao-ying, et al. Dynamic reliability analysis flexible mechanism based on support vector machine[J]. Journal of Mechanical Engineering, 2014, 50(11): 86-92. [本文引用:1]
[7]	李常有, 张义民, 王跃武. 线性连续系统的动态与渐变耦合可靠性分析[J]. 机械工程学报, 2012, 48(2): 23-28. Li Chang-you, Zhang Yi-min, Wang Yue-wu. Dynamic and gradual coupling reliability analysis of linear and continuous system[J]. Journal of Mechanical Engineering, 2012, 48(2): 23-28. [本文引用:1]
[8]	Li M, Azarm S, Aute V. A multi-objective genetic algorithm for robust design optimization[C]//ACM, New York, 2005: 771-778. [本文引用:1]
[9]	于繁华, 刘仁云. 车辆钢板弹簧的多目标可靠性稳健优化设计[J]. 吉林大学学报: 工学版, 2011, 41(增刊2): 226-230. Yu Fan-hua, Liu Ren-yun. Multi-objective reliability based on robust optimization design for vehicle leaf spring[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(Sup. 2): 226-230. [本文引用:1]
[10]	Fang Jian-guang, Gao Yun-kai, Sun Guang-yong, et al. Multi objective reliability-based ptimization for design of a vehicle door[J]. Finite Elements in Analysis and Design, 2013, 7(3): 13-21. [本文引用:1]
[11]	刘仁云, 张义民, 于繁华. 基于灰色粒子群算法的可靠性稳健优化设计[J]. 吉林大学学报: 工学版, 2006, 36(6): 893-897. Liu Ren-yun, Zhang Yi-min, Yu Fan-hua. Robust optimization design for reliability based on grey particle swarm algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2006, 36(6): 893-897. [本文引用:1]
[12]	邓聚龙. 灰色系统基本方法[M]. 武汉: 华中理工大学出版社, 1996: 70-75. [本文引用:1]
[13]	胡静, 曾建潮, 谭瑛. 动态环境下基于种群多样性的微粒群算法[J]. 系统仿真学报, 2007, 19(21): 4932-4935. Hu Jing, Zeng Jian-chao, Tan Ying. Particle swarm optimizer based on diversity of particle in dynamic environments[J]. Journal of System Simulation, 2007, 19(21): 4932-4935. [本文引用:1]

2013

0.0

... 近年来,关于机械零部件动态可靠性的研究已成为热点问题^[1,2,3] ...

2010

0.0

. 2010, 46(10):188-193 DOI:doi:10.3901/JME.2010.10.188

Dynamic reliability sensitivity analysis of mechanical components

机械零部件的动态可靠性灵敏度分析

Wang Xin-gang , Zhang Yi-min , Wang Bao-yan.

王新刚, 张义民, 王宝艳

传统的零部件可靠性模型不能很好地反映变幅随机载荷和强度退化对可靠性的影响,忽略可靠度和失效率随使用时间的变化规律.研究机械零件强度、载荷和可靠度随时间的变化规律,运用随机过程和顺序统计理论建立考虑变幅随机载荷和强度退化下机械零件的动态可靠性功能方程模型,利用二阶矩和摄动方法求出机械零部件的动态可靠性指标,并计算出零部件的动态可靠度.以建立的动态可靠性数学模型为基础,将可靠性设计理论与灵敏度分析方法相结合,提出动态可靠性灵敏度设计的计算方法,讨论动态可靠性灵敏度设计问题,以扭杆为例,给出各参数动态可靠性灵敏度的变化规律,分析设计参数的改变对扭杆可靠性的影响,为机械零部件的动态可靠性设计和动态灵敏度设计提供理论依据.

... 近年来,关于机械零部件动态可靠性的研究已成为热点问题^[1,2,3] ...

2010

0.0

. 2010, 46(3):188-197

Reliability modeling of systems with dependent failure when the life measured by the number of loadings

以载荷作用次数为寿命指标的失效相关系统可靠性建模

Wang Zheng , Kang Rui , Xie Li-yang.

王正, 康锐, 谢里阳

... 近年来,关于机械零部件动态可靠性的研究已成为热点问题^[1,2,3] ...

2012

0.0

. 2012, 34(2):214-218

Robust optimization design for reliability for coil spring based on multi-objective decision making methods

基于多目标优化策略的螺旋弹簧可靠性稳健优化设计

Liu Ren-yun , Hou Shu-fan , Zhang Yi-min.

刘仁云, 侯树范, 张义民

应用可靠性稳健优化设计理论和多目标决策方法,将车辆螺旋弹簧的可靠性稳健优化设计转化为多目标问题.运用层次分析法选取粒子群算法中的全局极值和个体极值,提出基于层次分析法的多目标粒子群算法,并将该算法应用于可靠性稳健优化设计的多目标模型求解中.与传统方法相比,该方法简便、易行,并能迅速准确地得到车辆螺旋弹簧的可靠性稳健优化设计信息.

... 研究者运用概率密度演化、顺序统计理论、随机摄动技术、支持向量机等方法进行了动态可靠性的研究,为动态可靠性研究提供了良好的基础^[4,5,6,7] ...

2007

0.0

2014

0.0

. 2014, 50(11):86-92 DOI:doi:10.3901/JME.2014.11.086

Dynamic reliability analysis flexible mechanism based on support vector machine

基于支持向量机柔性机构动态可靠性分析

Han Yan-bin , Bai Guang-chen , Li Xiao-ying

韩彦彬, 白广忱, 李晓颖

摘　要：针对柔性机构可靠性分析中计算效率低和精度差的问题,提出一种柔性机构动态可靠性分析的支持向量机回归极值法.该方法利用蒙特卡洛法抽取柔性机构动态响应极值的小样本;基于这些样本和支持向量机回归理论,建立柔性机构动态响应极值的代理模型;使用该代理模型进行柔性机构动态响应可靠性分析.结合曲柄摇杆柔性机构实例,利用支持向量机回归极值法、蒙特卡罗法、人工神经网络代理模型和二次响应面代理模型方法,分别对连杆的变形和摇杆的摆角进行可靠性分析,通过对四种方法计算结果的比较,证明了支持向量机回归极值法在柔性机构动态可靠性分析中高效率和高精度,验证了支持向量机回归极值法在柔性机构动态可靠性分析的可行性和适用性.

2012

0.0

. 2012, 48(2):23-28 DOI:doi:10.3901/JME.2012.02.023

Dynamic and gradual coupling reliability analysis of linear and continuous system

线性连续系统的动态与渐变耦合可靠性分析

Li Chang-you , Zhang Yi-min , Wang Yue-wu.

李常有, 张义民, 王跃武

机械设备的零部件通常承载着动态载荷,且由于制造的不确定性致使几何元素的尺寸、形状以及相互位置具有随机性,同时多于80%的零部件都是由于某些量的劣化导致渐变失效,因此,开展动态与渐变耦合可靠性研究对于机械行业的发展具有极为重要的意义。研究随机参数线性连续系统遭受强度劣化和承受动态载荷时的可靠性问题。根据线性连续系统的随机动力学理论获得随机响应的计算公式,由此建立随机交变应力的计算模型。采用一随机变量描述初始强度的不确定性,利用非平稳Gamma过程描述强度劣化量的演变过程。在此基础上构建线性连续系统的动态与渐变耦合状态函数和可靠度表达式。应用提出的方法分析轴扭转振动系统的动态与渐变耦合可靠性,将当量正态化法和设计验算点法相结合以估算动态与渐变耦合可靠度,采用中心差分方法分析该可靠度的敏感性。利用数值实例验证提出方法的实用性和有效性。结果表明, 提出的动态与渐变耦合可靠性分析方法能够有效解决随机参数线性连续系统遭受强度劣化和承受动态载荷时的可靠性分析问题。

2005

0.0

... 国内外学者们运用遗传算法和群智能算法来解决可靠性稳健优化多目标设计模型的求解问题^[8,9,10,11] ...

2011

0.0

. 2011, 41(增刊2):226-230

Multi-objective reliability based on robust optimization design for vehicle leaf spring

车辆钢板弹簧的多目标可靠性稳健优化设计

Yu Fan-hua , Liu Ren-yun.

于繁华, 刘仁云

... 国内外学者们运用遗传算法和群智能算法来解决可靠性稳健优化多目标设计模型的求解问题^[8,9,10,11] ...

2013

0.0

... 国内外学者们运用遗传算法和群智能算法来解决可靠性稳健优化多目标设计模型的求解问题^[8,9,10,11] ...

2006

0.0

. 2006, 36(6):893-897 DOI:doi:10.3969/j.issn.1671-5497.2006.06.013

Robust optimization design for reliability based on grey particle swarm algorithm

基于灰色粒子群算法的可靠性稳健优化设计

Liu Ren-yun , Zhang Yi-min , Yu Fan-hua.

刘仁云, 张义民, 于繁华

为提高车辆零部件的安全性和稳健性，应用可靠性稳健优化设计理论和多目标决策方法，将车辆前轴的可靠性稳健优化设计转化为多目标优化问题。运用灰色理论中的关联分析法，选取粒子群算法中的全局极值和个体极值，提出了适合可靠性稳健优化设计中多目标模型求解的灰色粒子群算法。与传统方法相比，该方法更能迅速准确地得到车辆前轴的可靠性稳健优化设计信息。

... 国内外学者们运用遗传算法和群智能算法来解决可靠性稳健优化多目标设计模型的求解问题^[8,9,10,11] ...

1996

0.0

... 1 灰色关联分析在灰色系统中比较事物、因素之间的动态发展相似程度是通过计算灰色关联度来实现的,即灰色关联度值越大,说明事物之间的相似程度就越高,否则就越低^[12] ...

2007

0.0

. 2007, 19(21):4932-4935 DOI:doi:10.3969/j.issn.1004-731X.2007.21.021

Particle swarm optimizer based on diversity of particle in dynamic environments

动态环境下基于种群多样性的微粒群算法

Hu Jing , Zeng Jian-chao , Tan Ying.

胡静, 曾建潮, 谭瑛

针对现有环境检测和环境响应方法存在的不足,提出了改进的基于微粒自身信息的检测方法,不仅降低了的算法复杂度,而且弥补了常用检测方法的局限性.同时还提出了种群多样性和微粒逃逸行为相结合的新型响应方法,将改进的检测和响应方法应用于各种复杂变化的抛物线函数中,结果表明该算法在动态环境中的有效性.

... 如果出现前、后代粒子的位置接近而对应适应度值却显著不同,基本上可以推断环境发生了变化^[13] ...