作者简介:石文孝(1960-),男,教授,博士生导师.研究方向:无线资源管理技术,Mesh网络技术和无线光通信.E-mail:swx@jlu.edu.cn
针对无线Mesh网络中传输链路负载不均衡的问题,使用混合整数线性规划问题表示联合信道分配、路由度量以及网络接口分配的优化模型,提出一种快速收敛的启发式算法(ILSG)求解规划问题。ILSG算法使用考虑网络连通性以及负载均衡的贪婪算法生成可用初始值,将初始值代入局部迭代搜索法(ILS)获得规划结果并确定网络资源分配方案。仿真结果表明:ILSG算法可以以更快的收敛速度得到优化模型的分配策略,在保证网络公平性的基础上提升了网络性能。
To solve the problem of load imbalance in Wireless Mesh Network (WMN), an optimization model is used in this work. This model jointly considers channel assignment, routing and interface allocation by making use of mixed integer linear programming. A heuristic algorithm (ILSG) with fast convergence rate is proposed to solve the programming problem. The ILSG algorithm considers network connectivity and load balance to get initial value, which is plugged into iterated local search algorithm to obtain the resource allocation results. Simulation results indicate that the ILSG algorithm can not get the allocation results with a faster convergence speed, but also improve the network performance on the basis of ensuring the fairness.
无线Mesh网络(Wireless mesh network, WMN)具有部署安装简单、稳定性好、带宽高的特点, 是解决通信网络“ 最后一公里” 问题的关键技术之一[1]。WMN可以通过信道分配[2, 3]和路由度量[4, 5]等方法优化网络性能。
目前, 已有很多学者对联合信道分配和路由度量优化网络性能进行了研究。Jia等[6]采用线性规划法在网络层提高吞吐量, 使用遗传算法进行信道分配与功率控制的联合优化, 但遗传算法容易造成早熟现象, 只能得到局部最优解。Zhang等[7]提出了一种分布式的联合信道分配和路由度量算法, 该算法在AODV(Ad hoc on-demand distance vector routing)路由协议传递信息的过程中添加了可分配的信道列表, 在完成信道分配后, 发送RTS-CTS(Request to send-clear to send)组合信息来完成信道分配, 但该算法没有从网络的整体去考虑如何分配路由和信道。Pham等[8]提出了一种联合信道分配、路由度量与接口分配的JCIAR(Jointing channel allocation, interface assignment and routing)算法, 该算法首先寻找网络最佳路径, 然后在此基础上得到最佳的接口分配和信道分配结果。Gá lvez等[9]提出一种启发式算法, 该算法通过删去无用边来降低模型复杂度, 分配速率后进行信道和路由的分配, 得到联合路由度量、信道分配、链路速率和调度的网络优化模型的分配结果。但是, 上述两种算法没有考虑联合优化时各因素之间的相互作用。Bakhshi等[10]针对多接口多信道WMN提出了一种即时联合QoS(Quality of service)路由度量和信道分配优化算法, 该算法寻找
路由度量和信道分配共同影响网络性能, 且二者之间可以相互影响, 路由度量的结果影响信道之间的干扰进而影响信道分配的结果, 反之信道分配的结果也会影响路由的选择, 把二者联合起来可以更好地优化网络性能。但是目前很多优化算法没有考虑路由与信道的相互影响, 或者存在算法计算量较大的问题。本文综合考虑路由度量、信道和网络接口的分配, 以及网络中的负载均衡问题, 利用混合整数线性规划问题表示优化模型。提出了使用考虑网络连通性以及负载均衡的贪婪算法生成可用初始值, 并将初始值代入ILS算法使其快速收敛的ILSG(Iterated local search with greedy)算法。仿真结果表明, ILSG算法收敛速度更快, 能获得有效的优化模型分配结果。
定义一个网络的物理拓扑图G(N, E), 其中N={1, 2, …, |N|}表示节点的集合, E={1, 2, …, |E|}表示节点间的单向边的集合。任意节点n∈ N代表一个静态的无线Mesh路由器。对于任意两个节点a、b∈ N, 如果a与b互相在对方的传输范围之内, 则a、b之间存在两条物理链路eab 、eba∈ E。每个无线路由器有I个网络接口, C={1, 2, …, |C|}表示网络中正交信道集合。
对于网络中任意两个节点a、b(e_ab∈ E)和任意的正交信道集合c∈ {1, 2, …, |C|}, 定义一个变量
对于网络中每个节点分配的信道, 定义一个变量
网络中每个节点都有固定的接口数, 每个节点连接的不同信道数量不能超过节点接口数, 即:
当网络中某节点使用次数较多时, 同一条信道可能会被此节点多次使用, 但是当多条链路使用同一接口, 由于同一时间只有一条链路可以使用该接口, 会降低链路的有效容量。因此, 限制每个节点使用同一条信道的次数:
考虑网络中的链路容量以及干扰问题, 假设R0是IEEE802.11a标准的链路层数据速率, 定义
假设网络中的两条链路eij 、epq, 如果eij 任意端点在epq 的任意端点的干扰范围之内, 则eij 与epq 互为干扰链路。对于网络中一条链路eab, 定义一个集合Lab⊂E, Lab 代表链路ab相互干扰边的集合, eba∈ Lab 。考虑网络中的干扰, 可以得到[14]:
式中:m、n为网络中任意两节点;
考虑网络中存在的传输流, 假定源节点s和目的节点d, rsd表示从节点s向节点d发送数据包的传输速率。定义一个传输流变量
当节点s向节点d发送数据包时, 经过链路eab, 如果a, b之间的链路在多条信道上传输, 不同信道的时延不同, 可能会导致数据包到达的顺序混乱。为了避免这一现象, 一条传输流在两个节点之间通过时, 只在一条信道上进行传输, 即:
定义变量
在实际网络中, 某条链路传输流的总速率不能超过该链路的标准链路层速率一定比例, 将这个比例称为链路占用率:
式中:
当一条链路的链路占用率过大时, 会出现时延增加, 丢包率变大的情况。为保证网络性能, 链路占用率不能太大, 考虑网络中的负载均衡, 将占用率大的链路的传输流分配到占用率较小的链路, 提出目标函数最小化μ 。
当网络中存在传输流时, 要确保传输流是可行流, 即, 对于节点
另外, 当节点
式中:ε 为一个不小于1的实数; hsd 为从节点s到节点d的最小跳数; ε hsd在数据包传输时, 所能接受的最大跳数。
由式(7)可得:
由式(9)(10)(13)可得:
由式(6)(9)(10)得:
由式(1)~(15), 得到混合整数线性规划问题:
式中:
令W代表源和目的节点对的数目, |N|、|E|和|C|分别是集合N、E和C的基数。由式(16)可以得出, 混合整数线性规划有
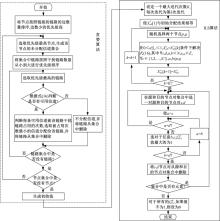
求解式(16)混合整数线性规划问题的计算量会随着网络规模的扩大而显著增大。因此, 需要采用一个高效的启发式算法来对规划问题求解。本文使用ILS算法来解决混合整数线性规划问题。但是, ILS算法收敛速度慢, 计算时间长, 不适用于式(16)混合整数线性规划问题。为提高算法效率, 加快收敛速度, 提出ILSG算法。ILSG算法具体流程图如图1所示。
如图1所示, ILSG算法主体分为两部分:第一部分用贪婪算法生成可行初始值; 二是将初始值代入ILS算法获得分配结果。
文献[13]所提贪婪算法只考虑初始值的可行性, 没有考虑迭代时的收敛速度。考虑规划模型达到优化网络公平性, 提出考虑网络公平性的贪婪算法, 同时为尽可能多的链路分配信道, 形成一个初始值。
贪婪算法首先将节点按照连接边数从小到大排序, 然后先为连接边数小的节点分配链路, 尽可能保证所有节点的连通性。
将每个节点的链路按照干扰链路数的多少进行优先级排序, 干扰链路少的优先级高, 然后按照优先级从高到低的顺序进行信道分配。
对于每条信道, 首先考虑此信道是否对此链路可用, 如果有多信道可用, 则考虑各信道被已分配干扰链路占用的次数, 再选择被占用次数最少的信道分配给该链路。
贪婪算法形成的初始值保证了网络的连通性, 将其代入ILS算法时, 可以使ILS算法得到一个可行的初始值, 同时可以更快地收敛, 达到降低算法计算量和减少计算时间的目的。
ILS算法设定一个最大迭代次数, 以防止算法的运行量过大。将贪婪算法获得的初始值代入ILS算法, 在每次迭代过程中, 随机选择两个节点p、q, 除了p、q两个节点使用的链路外, 其他链路都被分配一条初始信道。整数变量
采用Matlab和NS3进行ILSG算法性能仿真。在1000 m× 1000 m的区域内随机部署30个节点进行仿真试验, 每个节点配置3个接口, 可用信道数为4。设网络传输流为CBR(Constant bite rate)流, 数据包长度为1024 Byte, 最大迭代次数
本文采用以下指标对算法进行评价。
(1)收敛次数:迭代过程中, 目标函数值达到最优值的最小迭代次数。
(2)最大链路占用率:同一时间一条逻辑链路及其干扰范围内的链路传输速率与该链路容量的比值, 即式(10)中的μ 。
(3)网络吞吐量:单位时间内网络中所有目的节点成功接收的比特数, 其表达式如下:
式中:T为网络吞吐量; Nf 为网络中传输流的个数; Ji 为传输流i的接收节点成功接收到数据包的比特数; tend为接收最后一个数据包的时间; tstart为发送第一个数据包的时间。
(4)平均端到端时延:网络中所有数据包从源到目的节点的平均传输时间。
式中:D为平均端到端时延; Dj为数据包j的端到端时延; Nr为目的节点成功接收数据包的数目。
(5)网络平均丢包率:网络中所有没有成功传输的数据包数量与发送数据包总数量比值。
式中:
(6)网络公平性:若一个网络结构在相似网络负载以及传输情况下各节点可以获得接近的网络性能, 则这个网络具有高网络公平性。使用Jain等[15]提出的网络公平性指标:
式中:Ψ PDR为网络公平性; P为数据包递交率(Packet delivery ratio, PDR), 是一个目的节点接收到的数据包与其对应源节点发送数据包的数量的比值;
改变网络中的流数, 将文献[9]算法(本文将其命名为UILS(Used iterated local search)算法), 观察在传输流数量不同的情况下, ILSG算法与UILS算法的收敛次数, 所得仿真结果如表1所示。从表1可以看出, 由于所选择的源和目的节点对的不同, 两种算法的收敛次数呈现不规律的变化, 但是ILSG算法的收敛速度始终优于UILS算法。
| 表1 收敛次数比较 Table 1 Comparison of convergence times |
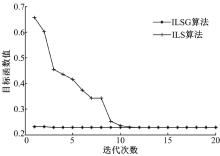
考虑ILS算法初始值链路占用率大, 如果传输速率过大, 会超出链路承受范围。选取较小传输速率, 保持网络中传输流数量为30, 源和目的节点对一致, 比较ILSG算法和ILS算法的收敛情况, 仿真结果如图2所示。
从图2可以看出, 两种算法都在不断向最优解方向接近, 但是ILSG算法的收敛明显比ILS算法要快, 可以降低算法计算次数, 从而降低算法复杂度。
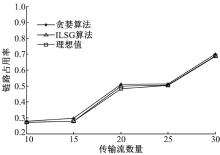
固定节点数量为30, 在不同传输流个数下对算法网络性能进行比较。首先使用贪婪算法进行初始信道分配, 基于信道分配结果使用文中优化模型式(16)进行路由度量, 文中表示为贪婪算法; 然后利用分支定界法[16]求得算法优化理想值。将ILSG算法与贪婪算法以及理想值进行仿真比较。仿真结果如图3所示。
从图3可以看出, ILSG算法链路占用率低于贪婪算法, 证明联合优化可以更好地利用网络资源, 提升网络性能。混合整数线性规划的算法复杂度取决于所含整数变量[16], ILSG算法使用更低的算法复杂度解决规划模型, 同时链路占用率与理想值接近, 证明了ILSG算法的可行性。
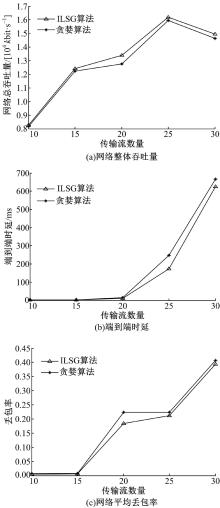
固定节点数量为30, 在不同传输流个数下对算法网络性能进行比较, 仿真结果如图4所示。
从图4可以看出, 在网络中传输流数量在一定范围内增加时, 网络平均吞吐量随传输流数量增加而增大。但是当网络中传输流数量足够大时, 吞吐量会变小, 这是因为当网络中传输流数量过大时, 会造成网络拥塞, 丢包率变大, 网络中的时延越来越大。从图4可以看出, 当网络中传输流数量较少时, 两种算法的网络性能相差不大, 但是随着传输流数的增加, ILSG算法网络性能要优于贪婪算法, 因为ILSG算法模型对信道与路由进行联合优化, 考虑信道分配与路由间的相互影响, 使网络资源得到充分的利用, 优化了网络性能。
改变网络中的流数, 比较两种算法分配结果的网络公平性, 所得结果如表2所示。从表2可以看出, 当网络中传输流数量较少时, 每种结构都能以高公平性传输数据包, 这是因为网络中传输流数量较少时, 每条传输流都以较高的递交率进行传递。但是当网络中传输流增多时, 网络公平性下降, 可以看出ILSG算法公平性要优于贪婪算法。因为当网络中传输流数量很多时, 网络中传输流开始呈现不同的递交率, 此时考虑信道与路由联合优化可以更好地利用网络资源, 提高网络性能。
| 表2 网络公平性比较 Table 2 Comparison of network fairness |
本文在WMN环境下用混合整数线性规划问题表示联合信道分配、路由度量与网络接口分配优化模型, 在ILS算法基础上, 提出ILSG算法来解决该规划问题。ILSG算法在ILS算法基础上先采用贪婪算法, 综合考虑网络连通性、模型可用性和公平性, 形成可用的ILS初始值, 然后采用ILS算法获得最终资源分配结果。仿真结果表明:ILSG算法能够以更快的速度收敛到最优解, 同时可以高效地获得构建优化模型的资源分配策略; 在保证网络资源分配合理性的前提下, 加强了网络公平性, 提升了网络的整体性能。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|