基于信号蝴蝶效应提取的无线传感网络失效区域检测

引用本文

唐锟, 施荣华. 基于信号蝴蝶效应提取的无线传感网络失效区域检测[J].吉林大学学报（工学版）, 2017,47(6): 1939-1948
TANG Kun, SHI Rong-hua. Detection of wireless sensor network failure area based on butterfly effect signal[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1939-1948 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706036
Permissions

基于信号蝴蝶效应提取的无线传感网络失效区域检测

唐锟, 施荣华

中南大学信息科学与工程学院,长沙 410083

通讯作者：施荣华(1963-),男,教授,博士生导师.研究方向:量子通信,计算机网络与安全,无线传感网络.E-mail:shirh@csu.edu.cn

作者简介:唐锟(1985-),男,博士研究生.研究方向:无线认知通信与安全,无线传感网络.E-mail:tk-0206@163.com

基金:湖南省教育厅科研项目(12A054); 国家自然科学基金项目(61201086)

摘要

针对无线传感网络(WSN)区域失效检测存在的范围精度低、误差大的问题,提出了一种WSN失效检测新模型。分析了WSN失效早期的信号特征,证明网络在失效前、后存在节点蝴蝶效应变化。引入虚拟区域的多维对偶模型,利用失效发生时,WSN节点蝴蝶效应变化在空间中表现出的对偶特征,对WSN中可能存在的失效风险进行检测,保证网络在不降低服务可用性的条件下完成失效区域检测。试验结果表明:该方法能够定量分析WSN失效对其安全性能的影响,且无需增加网络负担。

关键词: 信息处理技术; 无线传感网络; 失效性; 蝴蝶效应性; 模拟区域; 对偶特性

中图分类号:TH691.9 文献标志码:A 文章编号:1671-5497(2017)06-1939-10

Detection of wireless sensor network failure area based on butterfly effect signal

TANG Kun, SHI Rong-hua

School of Information Science and Engineering, Central South University, Changsha 410083, China

Abstract

In order to solve the problem of the low precision and large error in the area failure detection of Wireless Sensor Network (WSN), a new model for WSN failure detection is proposed. The signal characteristics of early failure in WSN are analyzed, and the butterfly effect of nodes is proved before and after the failure. By introducing the virtual multidimensional dual model area, and applying the dual characteristics in the space change of the butterfly effect of WSN node when the failure occurring, the risk of the failure existing in the WSN is detected, to ensure that the detection of network failure area does not reduce the service availability conditions. Experimental results show that the proposed method can quantitatively analyze the impact of WSN failure on its security performance without increasing the network burden.

Keyword: information processing technology; wireless sensor networks(WSN); failure; butterfly effect; simulation area; dual characteristics

Show Figures

0 引言

无线传感网络(Wireless sensor networks, WSN)节点的工作性能影响着传感网络的工作性能^[1]。一旦WSN在部分区域发生失效或者均衡性改变, 会对相关生产安全带来无法想象的灾难^[2]。因此, 对WSN失效的准确检测, 是提高工业现场安全性的重要保障。

目前, 已有很多学者研究了相关的WSN安全性能评估方法。文献[3]提出通过层次分析法评估WSN性能, 但是该方法是基于专家打分的方式实现评估, 主观性较高。文献[4]基于层次分析法获取网络安全参数特征的权重, 同样主观性较强。文献[5]只对3个获取属性权重的算法进行了分析, 但是未分析这些方法的实际应用过程。文献[6]对比分析了几种定位算法, 但是未对实际应用过程进行验证, 缺少客观性。文献[7]通过随机Petri网评价面向WSN结构的安全性能, 这种方法需要大量的先验知识作为支撑条件, 限制了其应用。文献[8]提出了针对WSN组合安全性能和可靠性瓶颈进行闭环分析的随机方法, 但是由于引入了多模型, 模型之间没有统一的衡量标准, 导致检测目标不明确。文献[9]在环境监测中使用(Unified modeling language, UML)表示WSN安全分析模型, 将结构图、故障树以及马尔可夫模型融入该模型, 实现了模型的自主映射, 进而研究了传感网络安全性检测的有效性。但是, 这种方法需要大量的计算, 很容易出现延迟, 应用效果不好。文献[10]通过排队方法对WSN软、硬件失效状态时的多层模块安全性进行分析, 该方法采用的排队网是一种乘积网, 具有一定的局限性。文献[11]在检测WSN稳定性和安全性时, 采用比特错误率的观点分析网络全部任务的运行状态、服务间的状态转移过程以及网络工作的环境, 进而定量分析网络的失效过程。并且面向不同运行场景, 通过离散时间马尔可夫链属性, 对服务组合的稳定性进行分析, 但是因为约束条件过多, 导致效果不佳。文献[12, 13]采用混合免疫方法改进错误率干扰下的WSN测试性能, 但是该种方法耗时严重。

以上方法虽然取得了一些进展, 但大部分方法过于依赖专家经验, 且需要在网络内部存在失效节点的状态下进行, 若WSN软、硬件不能正常运行, 将导致网络安全性检测服务的稳定性降低, 使得网络内部节点操作过程中耗费较多资源, 极大削减了网络的操作性能、有效性以及应用性。本文在对WSN安全性能进行建模和分析的基础上, 对失效检测过程中, 不同故障产生的失效对性能的干扰进行了全面分析, 同时在模拟数学空间中, 对软、硬件可能存在的失效风险进行了统一表达, 评估了失效风险对网络服务质量的影响, 为WSN失效检测提供了理论参考。

1 WSN服务失效节点的蝴蝶效应特征提取

1.1 WSN失效下的节点蝴蝶效应性证明

WSN主要依据节点中的服务软、硬件, 结合服务链路实现通信。一般的WSN中, 软件或者硬件节点无法工作, 将导致节点信号出现异常, 造成节点不停重传。若计算节点间仅存在一条通信物理链路, 则在网络通信过程中, 软、硬件无法正常工作后, 将无法完成服务, 执行的任务也会终止。因为传感网络的软、硬件多采用冗余结构设计, 失效描述具有时变性, 网络失效行为基本无法直接建模。本文选择如下处理方式:若WSN失效仅导致传输延迟的增加, 则将其看作链路失效模型进行处理; 若失效导致通信动作失败, 引起网络节点硬件出现故障, 则将其看作硬件失效进行处理。在有效执行阶段, 任务不断进入计算节点, 执行后传输至下一节点。在失效阶段, 各种失效类型与恢复策略对节点行为的影响存在很大差异。表1为WSN执行阶段几种常见的恢复手段。

表1 几种常见的WSN失效原因、结果及恢复手段 Table 1 Causes, results and recovery methods of several common wireless sensor networks

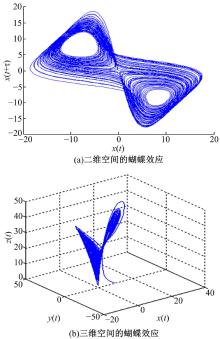
从表1可以看出:大部分节点失效行为产生后, 都有着重试、替换、局部重构的过程, 重试不但支持单个任务重新完成, 也支持WSN的整体复位。替换技术是节点出现失效后, 前驱服务任务被分配至其他替代服务中, 执行完之后传输至业务流程给出的后继服务节点中。局部重构是针对被单个失效节点干扰的情况, 对其局部进行重建。由于局部传感网络区域重建可看成更大区域和更多次数的替换, 所以其对安全性能的衡量结果是相同的。在失效过程前端, 即传感网络只是发生了初步失效行为, 还在进行重试、替换、局部重构的阶段, 大量节点会被重试、替换、局部重构, 导致传感网络节点的非线性成分大幅上升。而这种增加的失效节点处理过程与网络正常节点信号之间存在对立, 形成节点高度随机性纠缠, 这种随机性与真实的随机性之间存在较大的差别, 称为伪随机过程。伪随机过程在数学上可以用一种蝴蝶效应性来描述, 使得WSN在失效前期, 存在一定蝴蝶抗毁性效应^[14], 原因如下:

(1)WSN确定性和对立性的统一是蝴蝶效应的基本概念之一, 一旦软、硬件失效, 会使节点具有看似随机但又非真正随机的一种特征, 也称为蝴蝶效应性。

(2)WSN发生失效的情况下, 节点在对应的参数空间范围内, 会出现长期行为对初始状态的敏感依赖性。

(3)这种节点蝴蝶效应特征是WSN发生失效早期判断的一个重要前提条件。

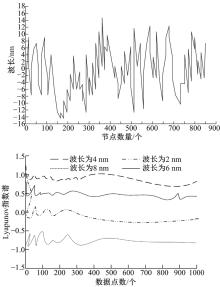
证明WSN失效早期节点有蝴蝶效应, 可通过上述节点序列的最大Lyapunov指数是否超过0进行验证。图1为WSN出现访问篡改失效下, 通过Matlab完成对获取的失效节点的Lyapunov指数图仿真^[15]。

	Figure Option View Download New Window
	图1 WSN失效早期节点序列蝴蝶效应性图谱Fig.1 Wireless sensor network, failure, early node sequence, butterfly effect

从图1可以看出:失效节点序列的最大Lyapunov指数大于0, 说明网络在早期失效时, 失效节点序列产生蝴蝶效应性。

1.2 WSN失效状态下蝴蝶效应特征分类和提取

由于蝴蝶效应特征是WSN失效的早期特征, 因此, 可作为判断传感网络失效征兆的一个信息来源。通过寻求网络失效节点蝴蝶效应特征, 分析WSN在失效早期的节点特征、内在变化规律及内部关系, 在非线性时间序列中寻找能反映网络软件和硬件失效特征的蝴蝶效应节点特征关联^[16], 进行相应的特征提取, 可以有效地形成失效判断, 方法如下:以节点分类器为依据, 将WSN失效后, 节点分类中的误码率变换为一系列概率密度函数, 以这一系列密度函数为依据, 分配不同的使用概率。依据概率分析形成可以反映节点明显蝴蝶效应特征的特定随机数序列, 得到具有蝴蝶效应的特征节点。

失效节点能够达到概率密度的所有任意调配要求。假设 $\begin{matrix} x (n) \end{matrix}$ 为失效节点序列, $\begin{matrix} τ \end{matrix}$ 为空间重构的最大延迟。在给定的重构映射 $\begin{matrix} m \end{matrix}$ 维相空间内, 产生 $\begin{matrix} m \end{matrix}$ 维矢量, 利用式(1)表述^[17]:

$\begin{matrix} X (n) = {x (n), x (n + τ), \dots, x (n + (m - 1) τ)} (1) \end{matrix}$

式中: $\begin{matrix} n = 1, 2, \dots, N 。 \end{matrix}$

在 $\begin{matrix} m \end{matrix}$ 维相空间重构映射以后, 给出一维数向量 $\begin{matrix} X_{n}, \end{matrix}$ 一维数向量在相空间中表示一点, 与此点最相近的点表示为 $\begin{matrix} X_{η (n)}, \end{matrix}$ 将欧氏距离定义成距离尺度, 表述相邻两个节点间的距离 $\begin{matrix} R_{mn}, \end{matrix}$ 即:

$\begin{matrix} \begin{matrix} R_{mn} = ‖ X_{η (n)} - X_{n} ‖_{2}^{^{m}} = \\ \min_{j = N_{0}, \dots, N, j \neq n} ‖ X_{n} - X_{j} ‖_{2} = \\ \sqrt[]{\overset{m - 1}{\sum_{l = 0}} (x_{η (n) + lτ} - x_{n + lτ})^{2}} (2) \end{matrix} \end{matrix}$

当 $\begin{matrix} m \end{matrix}$ 增加到 $\begin{matrix} m + 1 \end{matrix}$ 时, 在其失效节点序列所映射的空间中, 利用式(3)表述相空间中任意一点与其最近邻点间的距离:

$\begin{matrix} \begin{matrix} R_{(m + 1) n} = ‖ X_{η (n)} - X_{n} ‖_{2}^{^{m + 1}} = \\ \sqrt[]{\overset{m}{\sum_{l = 0}} {(x_{η (n) + lτ} - x_{n + lτ})}^{2}} = \\ \sqrt[]{{[‖ X_{η (n)} - X_{n} ‖_{2}^{^{m}}]}^{2} + {(x_{η (n) + m τ} - x_{n + mτ})}^{2}} (3) \end{matrix} \end{matrix}$

将分类失效节点定义为 $\begin{matrix} Q_{s}, \end{matrix}$ 源节点定义为 $\begin{matrix} Q_{0}, \end{matrix}$ 将两者进行比较, 分辨两者间的差别, 依据分辨结果对失效概率进行判断, 并分析映射分类是否可以成立。随机搜索一组失效概率映射节点 $\begin{matrix} Q_{s} \end{matrix}$ 的平均值 $\begin{matrix} < Q_{s} >, \end{matrix}$ 利用该值与源节点 $\begin{matrix} Q_{0} \end{matrix}$ 比较, 衡量映射节点 $\begin{matrix} Q_{s} \end{matrix}$ 的误差影响, 标记为 $\begin{matrix} σ_{s} 。 \end{matrix}$ 当 $\begin{matrix} < Q_{s} > \end{matrix}$ 一定时, 若 $\begin{matrix} σ_{s} \end{matrix}$ 取值偏大, 表示 $\begin{matrix} Q_{s} \end{matrix}$ 离散化越高, 在特殊情况下, $\begin{matrix} Q_{s} \end{matrix}$ 与 $\begin{matrix} Q_{0} \end{matrix}$ 相邻, 这些节点与 $\begin{matrix} Q_{0} \end{matrix}$ 的差异性相对较小; 反之, $\begin{matrix} < Q_{s} > \end{matrix}$ 与 $\begin{matrix} Q_{0} \end{matrix}$ 的差异性较大。因此, 可以用差别显著度 $\begin{matrix} S \end{matrix}$ 表示邻居节点与源节点的差异性:

$\begin{matrix} S = |< Q_{s} > - Q_{0}| / σ_{s} (4) \end{matrix}$

式中: $\begin{matrix} < Q_{s} > \end{matrix}$ 为映射节点判别统计量值的均值; $\begin{matrix} σ_{s} \end{matrix}$ 为映射标准差, 即:

$\begin{matrix} σ_{s} = \sqrt[]{\frac{1}{N - 1} \overset{N}{\sum_{i = 1}} {(Q_{i} - < Q_{s} >)}^{2}} (5) \end{matrix}$

采用Sigma检验, 假设每个概率失效节点, 其 $\begin{matrix} Q_{s} \end{matrix}$ 值的概率分布是较为普遍的正态分布, 则:

$\begin{matrix} \begin{matrix} p (Q_{s}) = \frac{1}{\sqrt[]{2 π} σ_{s}} \exp [- \frac{{(Q_{s} - < Q_{s} >)}^{2}}{2 σ_{s}^{2}}] (6) \\ \int_{-}^{\infty} p (Q_{s}) d Q_{s} = 1 (7) \end{matrix} \end{matrix}$

优化分类模型的概率分析置信区间和拒绝区间的分类需要在进行失效节点分类的过程中充分进行考虑。区间展示图如图2所示, 其中, z₁ 、z₂ 分别为优化分类置信区间的上、下界。采用p(Q_s)~Q_s曲线描述, 判断分析映射分类是否合理需要满足相应条件: $\begin{matrix} S \end{matrix}$ 必须大到使 $\begin{matrix} Q_{s} \end{matrix}$ 的分布远离 $\begin{matrix} Q_{0}, \end{matrix}$ 或者说 $\begin{matrix} Q_{0} \end{matrix}$ 应在 $\begin{matrix} Q_{s} \end{matrix}$ 大部分分布之外。 $\begin{matrix} p (Q_{s} \end{matrix}$ )在相应的区间内可以延伸到 $\begin{matrix} Q_{s} \end{matrix}$ 取值无穷大, 这就使得 $\begin{matrix} Q_{0} \end{matrix}$ 完全在 $\begin{matrix} p (Q_{s} \end{matrix}$ )分布之外是不可能实现的。根据经验判断置信度为65%, 则概率不成立的机会α =35%, 即如果 $\begin{matrix} Q_{0} \end{matrix}$ 与 $\begin{matrix} < Q_{s} > \end{matrix}$ 的差异化超过阈值 $\begin{matrix} Q_{c}, \end{matrix}$ 使得:

$\begin{matrix} p (|Q_{0} - < Q_{s} >| > Q_{c}) \leq 0.35 (8) \end{matrix}$

	Figure Option View Download New Window
	图2 优化分类模型概率分析置信区间和拒绝区间Fig.2 Optimal classification model, probability analysis, confidence interval and rejection interval

说明 $\begin{matrix} Q_{0} \end{matrix}$ 只可能在图1中占 $\begin{matrix} p (Q_{s}) \end{matrix}$ 面积不到35%的阴影部分才与 $\begin{matrix} Q_{s} \end{matrix}$ 无差别, $\begin{matrix} Q_{0} \end{matrix}$ 与这些 $\begin{matrix} Q_{s} \end{matrix}$ 这样小的重合概率表示所有 $\begin{matrix} Q_{s} \end{matrix}$ 与 $\begin{matrix} Q_{0} \end{matrix}$ 的差别显著。由于正态分布在 $\begin{matrix} < Q_{s} > \end{matrix}$ 两侧对称的, 图1中两侧阴影部分(称为概率分析映射分类的拒绝区域)各占概率的2.5%。对于标准正态分布( $\begin{matrix} σ_{s} = 0, < Q_{s} > = 0 \end{matrix}$ ), 应有:

$\begin{matrix} 0.025 = \int_{-}^{\infty} p (Q_{s}) d Q_{s} = 1 - \int_{-}^{\infty} p (Q_{s}) d Q_{s} (9) \end{matrix}$

式中: $\begin{matrix} z_{2} = - z_{1} = 1.96 。 \end{matrix}$ 由此得:

$\begin{matrix} |< Q_{s} > - Q_{c}| / σ_{s} = z_{1} = 1.96 \approx 2.00 (10) \end{matrix}$

由此可得判据为:

(1) $\begin{matrix} S \geq 2.00, \end{matrix}$ 概率分析映射分类以95%概率不成立, 原失效节点是蝴蝶效应特征节点。

(2) $\begin{matrix} S < 2.00, \end{matrix}$ 概率分析映射分类成立, 原失效节点不是蝴蝶效应特征节点。

对于同类映射下的时间序列 $\begin{matrix} x_{i} (i = 1, 2, \dots, N), \end{matrix}$ 也可看成是WSN失效后的节点时间序列, 利用像空间重构理论重构出 $\begin{matrix} m \end{matrix}$ 维相空间, 给出相点 $\begin{matrix} x_{j} \end{matrix}$ 除本身外 $\begin{matrix} x_{i} \end{matrix}$ 的距离低于 $\begin{matrix} r \end{matrix}$ 的 $\begin{matrix} x_{j} \end{matrix}$ 点数:

$\begin{matrix} Q = \sum_{j \neq i} H (r - ‖ x_{i} - x_{j} ‖) (11) \end{matrix}$

式中:H(· )为Heavside函数。

将距离比给定的距离小的点, 占全部点的比例定义为关联函数, 表述为:

$\begin{matrix} C_{N} (r) = \frac{2}{N (N - 1)} \overset{N}{\sum_{i = 1}} \overset{N}{\sum_{j = i + 1}} H (r - ‖ x_{i} - x_{j} ‖) (12) \end{matrix}$

式(12)中, 分子为2是为了完全排除冗余数, 利用范数定义两个相点间的距离。获取两个相点间的距离, 将该距离定义为两个矢量的最大差分量:

$\begin{matrix} ‖ x_{i} - x_{j} ‖= \max_{1 \leq k \leq m} |x_{i - (k - 1) τ} - x_{j - (k - 1) τ}| (13) \end{matrix}$

对于距离不大于 $\begin{matrix} r \end{matrix}$ 的向量, 称为具有关联性的矢量, 完成关联挖掘规则的建立, 提取关联特征。在完成失效概率分类后, 失效蝴蝶效应节点特性会存在较长时间, 并且促使网络反复收缩, 失效节点像空间中的体积会在耗时的网络作用下体现, 这样形成了WSN节点在失效状态下的差异性, 即蝴蝶效应。传感网络失效节点序列形成的蝴蝶效应如图3所示。

	Figure Option View Download New Window
	图3 失效节点蝴蝶效应示意图Fig.3 Schematic of butterfly effect of failure node

蝴蝶效应是WSN在一定的失效状态下, 其形成结果是由于其节点具有差异性, 蝴蝶效应在空间中呈无序性发展状态, 可以通过是否能够迅速完成在虚拟空间中的对偶检查, 来验证蝴蝶效应是否延伸, 进而判定WSN是否失效。

2 引入蝴蝶效应对偶区域的失效对偶检测

2.1 基于对偶判断检测的可行性分析

三维空间中的对偶最早是被用于计算机三维视觉领域的研究, 其在计算机视觉中解决的问题与本文要解决的问题具有共性, 三维视觉重构中的空间是根据采集节点虚拟的, 这符合本文的应用条件。如果形成三维虚拟空间对偶必须满足如下要求:①解存在; ②解是唯一的; ③解是连续地依赖于输入节点。

满足以上要求, 即可在三维虚拟空间中形成对偶, 这也是对偶的充要条件, 第1节提到的蝴蝶效应空间特征很好地满足了这些特性, 因此会形成对偶。原因如下:

(1)文献[18]证明了当产生蝴蝶效应的节点是加性独立同分布约束时, 最大后验概率解是存在的。

(2)运用MRF(Multiple reference frames)方法^[19]通过先验分布模型对蝴蝶效应问题的解作某种约束, 通过样条函数作平滑约束, 可以保证蝴蝶效应中的对偶都是唯一解。

(3)本文蝴蝶效应的形成依赖WSN的连续失效节点, 因此, 满足失效输入节点的要求。

因此, 运用对偶理论处理虚拟空间中的对偶, 可以有效地检测WSN的早期失效过程。

2.2 对偶区域内失效有效性判断

在对偶信号检测策略中, 信号差值对比的方式在判断对偶蝴蝶效应上具备较好的性能, 其优点是节点存在干扰时, 具有稳定性。

设定一个节点的二维区域, 具体描述如下:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{x} = f (x, u, t) x \in R^{n}, u \in R^{m}, t \in R \\ y = h (x), y \in R^{l} \end{matrix} (14) \end{matrix}$

式中: $\begin{matrix} l \leq m \leq n 。 \end{matrix}$

设定节点跳变切换函数矢量为:

$\begin{matrix} s = s (x), s \in R^{m} (15) \end{matrix}$

判断阈值函数, 则:

$\begin{matrix} u_{i} = \{\begin{matrix} u_{i}^{+}, s (x) > 0 \\ u_{i}^{-}, s (x) < 0 \end{matrix} (16) \end{matrix}$

式中: $\begin{matrix} u_{i}^{+} (x) \neq u_{i}^{-} (x) (i = 1, 2, \dots, m); \end{matrix}$ 假设切换函数 $\begin{matrix} s (x) \end{matrix}$ 在一个指定的非零区域, 向量 $\begin{matrix} f^{+} = f (x, t, u^{+}) \end{matrix}$ 和 $\begin{matrix} f^{-} = f (x, t, u^{-}) \end{matrix}$ 位于法线上的投影存在符号指向相对的情况, 则式(14)描述的系统可产生蝴蝶效应。该状态存在的充分条件为:

$\begin{matrix} \lim_{s \to + 0} s < 0, \lim_{s \to + 0} s > 0 (17) \end{matrix}$

若节点的初始状态点 $\begin{matrix} x (0) \end{matrix}$ 不在 $\begin{matrix} s (x) = 0 \end{matrix}$ 附近, 在模拟空间的所有位置, 若是节点趋近于切换面 $\begin{matrix} s (x) = 0 \end{matrix}$ , 即满足了可达性条件, 则节点形成了蝴蝶效应中的对偶运动。

2.3 判断过程中干扰的排除

在存在振动的环境下, 可能会存在需要的蝴蝶对偶区域。需要其进行排除。

先给定两个节点, 如下所示:

$\{\begin{matrix} \overset{\cdot}{x} = f (x (t), t) + g \cdot u (t), x (0) = x_{0} \in R^{n} \\ y (t) = c (x) \end{matrix} (18)$

$\begin{matrix} \begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{d} = f_{d} (x_{d} (t), t), x_{d} (0) = x_{d 0} \in R^{n} \\ y_{d} (t) = c (x_{d}) \end{matrix} (19) \end{matrix} \end{matrix}$

式(18)所示的节点中, $\begin{matrix} x (t) \in R^{n} \end{matrix}$ 为状态向量; $\begin{matrix} f (x) = {[f_{1} (x) f_{2} (x) \dots f_{n} (x)]}^{T} 、 g \in R^{n \times 1} 、 u \in R \end{matrix}$ 均为控制向量; $\begin{matrix} y \in R \end{matrix}$ 为输出向量; $\begin{matrix} c : R^{n} \to R \end{matrix}$ 为非线性函数。式(19)代表目标节点, $\begin{matrix} x_{d} (t) \in R^{h} \end{matrix}$ 为状态向量; $\begin{matrix} f_{d} (x) = [f_{d 1} (x) f_{d 2} (x) \dots f_{dn} {(x)]}^{T} 、 y_{d} \in R \end{matrix}$ 为输出向量; $\begin{matrix} c : R^{n} \to R \end{matrix}$ 为非线性函数。

判断目标节点存在振动时, 节点需要满足:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{x} = f^{\cdot} (x (t), t) + Δf (x (t), t) \\ y (t) = cx \end{matrix} (20) \end{matrix}$

式中: $\begin{matrix} f^{\cdot} \end{matrix}$ 为节点标称参数; $\begin{matrix} Δf \end{matrix}$ 为不确定项。

利用切换函数, 获取振动作用u_vsc, 有u=u_npc+u_vsc使节点信息采集效果稳定, 其中外部振动由u_npc表示, 且满足采集误差条件, 即:

$\begin{matrix} \lim_{t \to \infty} e (t) = 0 (21) \end{matrix}$

基于以上步骤, 可使复杂的振动干扰实现统一目标采集。

3 测量试验及结果

3.1 试验环境设计

QPME(Queuing petri net modeling environ-ment)软件包是一款利用QPN特性的建模工具, 仿真试验结果表明, 利用QPME建模工具能够较好地反映和预测WSN的性能变化^{[20, 21]}。本文使用QPME软件包工具对前面阐述的基于蝴蝶效应的对偶数字测试模型和WSN仿真模型进行试验仿真, 在不同的WSN软件失效概率配置和硬件失效概率配置下, 分析模型对其安全性的检测性能。度量的属性主要包括WSN稳定状态下任务的吞吐率和网络平均响应时间、WSN硬件节点的利用率、WSN硬件节点执行任务的丢失率以及完成率。仿真节点的置信区间 $\begin{matrix} (c, i) \end{matrix}$ 为95%。WSN任务丢失率是指当WSN需要执行网络任务时, 由于WSN的相关硬件失效而被拒绝执行的网络任务数目占总任务数目的比例; WSN任务完成率是指WSN接受任务并成功实现传输到网络硬件和软件的概率。WSN工作任务仿真场景如图4所示, 利用开放式队列模型, 并通过队列库所 $\begin{matrix} Q (G / M / \infty / IS) \end{matrix}$ 模拟相对稳定状态下WSN执行任务的情况。

由于QPME不支持时间变迁, 因此QPME现有版本不能直接使用, 需要利用一个队列库所 $\begin{matrix} (G / M / 1 / PS) \end{matrix}$ 与瞬时变迁相结合, 替换时间变迁的模式。当I类WSN软、硬件出现失效时, 通过第IV类零队列处理方式对WSN冗余设备的替换进行模拟, 从而实现失效恢复。利用帧中继信息法对I类~IV类失效恢复花费的时间分布进行模拟, 通过软件架构对测试模型的总体执行情况进行跟踪和描述。WSN的失效类型概率分别为:

$\begin{matrix} \begin{matrix} pN (Ⅰ) = 5 %; pN (Ⅱ) = 45 %; \\ pN (Ⅲ) = 36 %; pN (Ⅳ) = 14 % 。 \end{matrix} \end{matrix}$

3.2 服务节点的失效测试结果分析

针对WSN软件硬件的失效测试, 设计和完成了2个试验。

试验1 利用蝴蝶效应特征对偶检测方法测试失效率, 计算其对WSN安全性能的影响。在进行试验时, 保证WSN中软、硬件失效概率不同, 对失效发生率进行调整, 得到失效队列库 $\begin{matrix} SF \end{matrix}$ 中节点数量p₁, 从而实现对服务节点性能变化趋势的观察, 结果如图5所示。其中, 每个子图的横轴表示队列库 $\begin{matrix} SF \end{matrix}$ 中节点数量p₁, 失效发生率随着p₁的变化而变化, 在每个子图中, 利用纵坐标对不同性能参数进行表示。

分析实际测试结果可得:随着p₁的变化, WSN发生失效的概率逐渐降低, WSN的响应速度加快, 其硬件利用率提高, 减小了任务的丢失概率, 从而提高了网络任务完成率。本文所提失效检测模型可以准确描述WSN各项性能指标随网络失效的变化趋势。

试验2 各类失效对WSN安全性能的影响分析。让WSN中硬件或者软件的某一类发生失效, 分析该类失效发生率变化对WSN安全性能的影响。将WSN中的任意3类失效发生的概率设为0, 则剩下一类的失效发生概率为100%, 对失效发生率进行调整, 得到失效队列库 $\begin{matrix} SF \end{matrix}$ 中节点数量p₁, 从而实现对服务节点性能变化趋势的观察。

	Figure Option View Download New Window
	图4 WSN的试验性QPN建模Fig.4 Experimental QPN modeling for wireless sensor networks

	Figure Option View Download New Window
	图5 试验1的仿真结果Fig.5 Simulation results of experiment 1

	Figure Option View Download New Window
	图6 试验2的仿真结果Fig.6 Simulation results of experiment 2

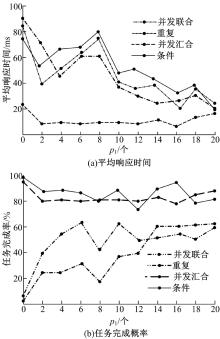
图6为试验2的仿真结果, 在每个子图中, 不同类型失效对WSN安全性能影响如4条曲线所示, 每个子图的横轴表示队列库 $\begin{matrix} SF \end{matrix}$ 中节点数量p₁, 失效发生率随着p₁的增加而逐渐降低。分析图6可知, 当p₁逐渐增加时, WSN硬件失效发生率逐渐降低, 对于I类失效, 网络硬件失效发生率降低将影响WSN的吞吐率, 使其逐渐提升, 并缩短了无线传感器节点响应时间, 降低了WSN传输任务丢失率, 同时提高了WSN任务传输成功率; 对于II类失效, 在WSN失效发生率下降的初始阶段, 网络吞吐率大幅度提升, 当网络失效发生率降低到一定程度时, WSN吞吐率提升变化幅度较为缓慢, 并逐渐趋于稳定, 可知II类失效发生率的不断降低对无线传感器节点的整体响应时间的影响不大, 但可以有效提升WSN硬件资源的可利用率, 将任务丢失量降低至最小, 由此提升了网络任务完成的成功几率; 对于III类失效, 重试机制虽然可以使WSN可处理的任务量大幅度增加, 提高了硬件利用率, 但是WSN硬件任务队列变长导致网络任务等待时间增加, 由此延长了WSN任务的整体处理时间, 当WSN失效率降低后, 传感器节点响应时间缩短, 网络硬件利用率下降, 提升了传感器节点任务的完成几率, 并且不会造成WSN任务的丢失, 也不影响节点任务吞吐率。

3.3 传感网络节点软、硬件失效测试结果分析

试验3具体过程如下所述:分别调节N₂、N₄、N₅、N₇的失效发生率, 其他试验参数保持不变, 分析失效应急机制对WSN整体运行性能的影响。

试验4的具体试验结果如图7所示, 其中:①各图中的4条曲线分别代表不同交互关系条件下, 网络安全性受到调整失效发生率的影响。②各图中的横轴为队列库 $\begin{matrix} SF \end{matrix}$ 中节点数量p₁, 当p₁逐渐下降时, 其相应的传感网络失效率就会增大。③子图中的纵轴代表传感网络安全性能的参数, 其响应时间以对数形式进行表示。

	Figure Option View Download New Window
	图7 试验4的仿真结果Fig.7 Simulation results of experiment 4

由图7可以得出:传感网络失效发生率随着其硬件的节点N_i 库SF中节点数量p₁ 下降而降低, 并且应急平均响应时间也随着其硬件的节点N_i 库SF中节点数量p₁增加而减少, 从而任务完成的概率有所上升。在不同的交互关系下, WSN的安全性能受到 $\begin{matrix} N_{i} \end{matrix}$ 的影响情况具体如下所述。

(1)当 $\begin{matrix} N_{2} \end{matrix}$ 失效发生率变化时, 可以将WSN安全性能的影响划分成两个阶段, 将N₂ 和N₃ 库SF的p₁ 均取值为8, 并设定该取值为界限。当N₂ 的p₁取值范围大于8时, WSN的平均响应时间将随着N₂ 失效率的降低而相应减小, 由此任务的完成概率将会上升; 当N₂ 的p₁取值范围小于8时, WSN的平均响应时间并不随着N₂ 失效率的降低而有太大变化, 然而任务的完成概率有显著上升。综上所述, 如果N₂ 失效发生率大于N₃ 失效发生率时, 那么由N₂ 决定N₂ 与N₃ 库同时运行的平均响应时间, 而N₃ 和N₂共同决定任务的完成概率。

(2)在重复关系中, $\begin{matrix} N_{4} \end{matrix}$ 失效发生率降低, 将会使WSN平均的响应时间严重减少, 使任务的完成概率迅猛提高。综上所述, N₄ 的迭代次数(k=3)扩大了N₄对WSN安全性的影响。

(3)在条件关系中, $\begin{matrix} N_{7} \end{matrix}$ 失效发生率的减小, 会使网络平均的响应时间有所降低, 所以任务完成的概率有所上升, 但其变化的趋势较为平缓。综上所述, 在该条件下网络安全性不易受到 $\begin{matrix} N_{7} \end{matrix}$ 的影响。

4 结束语

在不确定以及各种复杂的外部因素影响下, WSN不能安全、稳定地运行。随着WSN的快速演变以及网络结构逐渐复杂性的增加, 当前无线网络的安全性分析方法已不能满足需求。由此, 针对WSN发生失效后呈现出的蝴蝶效应等特点, 提出一种基于节点蝴蝶效应对偶检测的WSN失效检测方法。该方法首先依据WSN发生失效行为以后的节点之间的交互关系, 分析了网络性能受失效行为类型的影响。对网络节点蝴蝶效应进行建模, 根据蝴蝶效应产生的交互关系可得出对偶检测数学模型, 由此, 利用QPME 1.01软件包对失效检测模型定量的分析能力进行验证, 结果表明, 该方法可定量分析出WSN的失效率以及网络恢复的时间与节点交互关系, 并且分析了节点网络安全性能评价中产生的影响, 具有较好的有效性和可行性, 与当前的网络安全性能分析方法相对比, 本文方法存在以下优势:

(1)能够从多方面考虑WSN发生故障时的情况, 对不同故障产生的失效状况和恢复进行分析, 能够有效表达节点失效恢复运行下的安全机制。

(2)将WSN失效特征通过蝴蝶效应对偶的方式直观地加以表示, 尤其是对WSN失效蝴蝶效应特征计算过程进行描述, 能够将失效判断转换为模型上的对偶, 有效地解决了网络安全中存在的定量分析问题。

(3)通过与其他分析方法进行对比, 可对不同的WSN中节点失效的恢复方法进行判断, 且量化的准确性有所改善, 能够有效指导在不确定环境下WSN节点失效恢复实施方案的设计。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张超, 张凤鸣, 吴虎胜, 等. 航电系统失效检测优化方法研究与仿真[J]. 计算机仿真, 2014, 31(3): 100-104. Zhang Chao, Zhang Feng-ming, Wu Hu-sheng, et al. Research and simulation of optimization method for avionics system failure detection[J]. Computer Simulation, 2014, 31(3): 100-104. [本文引用:1]
[2]	滕志军, 张帆, 宋明辉. 无线传感器网络能量均衡蚁群路由算法[J]. 吉林大学学报: 工学版, 2016, 46(1): 327-332. Teng Zhi-jun, Zhang Fan, Song Ming-hui. Wireless sensor network energy balance ant colony routing algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(1): 327-332. [本文引用:1]
[3]	Azharuddin M, Jana P K. A distributed algorithm for energy efficient and fault tolerant routing in wireless sensor networks[J]. Wireless Networks, 2015, 21(1): 251-267. [本文引用:1]
[4]	Akhtar F, Rehmani M H. Energy replenishment using renewable and traditional energy resources for sustainable wireless sensor networks: a review[J]. Renewable & Sustainable Energy Reviews, 2015, 45(1): 769-784. [本文引用:1]
[5]	李建坡, 时明, 钟鑫鑫. 自适应蒙特卡罗无线传感器网络移动节点定位算法[J]. 吉林大学学报: 工学版, 2014, 44(4): 1191-1196. Li Jian-po, Shi Ming, Zhong Xin-xin. Self-adaptive Monte Carlo localization algorithm of mobile nodes in WSN[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(4): 1191-1196. [本文引用:1]
[6]	张婧, 刘衍珩, 张晋东, 等. 无线传感器网络簇半径自适应调整策略[J]. 吉林大学学报: 工学版, 2016, 46(3): 876-883. Zhang Jing, Liu Yan-heng, Zhang Jin-dong. Cluster size adaptive adjustable strategy for wireless sensor networks[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(3): 876-883. [本文引用:1]
[7]	Zhao M, Yang Y, Wang C. Mobile data gathering with load balanced clustering and dual data uploading in wireless sensor networks[J]. IEEE Transactions on Mobile Computing, 2015, 14(4): 770-785. [本文引用:1]
[8]	Li M, Lin H J. Design and implementation of smart home control systems based on wireless sensor networks and power line communications[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4430-4442. [本文引用:1]
[9]	张颖颖, 张帅, 张萍, 等. 融合对比度和分布性的图像显著性区域检测[J]. 光学精密工程, 2014, 22(4): 1012-1019. Zhang Ying-ying, Zhang Shuai, Zhang Ping. Detection of salient maps by fusion of contrast and distribution[J]. Optics and Precision Engineering, 2014, 22(4): 1012-1019. [本文引用:1]
[10]	王志繁, 叶庆卫, 周宇, 等. 基于排队论的低功耗无线传感技术及其应用[J]. 计算机工程, 2016, 42(8): 39-45. Wang Zhi-fan, Ye Qing-wei, Zhou Yu, et al. Low-power wireless sensing technology and its application based on queuing theory[J]. Computer Engineering, 2016, 42(8): 39-45. [本文引用:1]
[11]	徐涛, 贾松敏, 张国梁. 元胞自动机多尺度优化的显著性细微区域检测[J]. 光学精密工程, 2017, 25(5): 1312-1321. Xu Tao, Jia Song-min, Zhang Guo-liang. Salient subtle region accurate detection via cellular automata multi-scale optimization[J]. Optics and Precision Engineering, 2017, 25(5): 1312-1321. [本文引用:1]
[12]	王明伟, 陈立万, 李洪兵, 等. 基于混合免疫系统机理的无线传感网络故障检测算法[J]. 仪表技术与传感器, 2016(4): 84-86. Wang Ming-wei, Chen Li-wan, Li Hong-bing, et al. Fault detection algorithm for wireless sensor networks based on hybrid immune system mechanism[J]. Instrument Technique and Sensor, 2016(4): 84-86. [本文引用:1]
[13]	赵锡恒, 何小敏, 许亮, 等. 基于免疫危险理论的无线传感器网络节点故障诊断[J]. 传感技术学报, 2014, 27(5): 658-663. Zhao Xi-heng, He Xiao-min, Xu Liang, et al. Wireless sensor networks node fault diagnosis based on immune danger theory[J]. Chinese Journal of Sensors and Actuators, 2014, 27(5): 658-663. [本文引用:1]
[14]	李文锋, 符修文. 无线传感器网络抗毁性[J]. 计算机学报, 2015, 38(3): 625-647. Li Wen-feng, Fu Xiu-wen. Survey on invulnerability of wireless sensor networks[J]. Chinese Journal of Computers, 2015, 38(3): 625-647. [本文引用:1]
[15]	柯洪昌, 孙宏彬. 图像序列的显著性目标区域检测方法[J]. 中国光学, 2015, 8(5): 768-774. Ke Hong-chang, Sun Hong-bin. A saliency target area detection method of image sequence[J]. Chinese Journal of Optics, 2015, 8(5): 768-774. [本文引用:1]
[16]	He D, Kumar N, Chen J, et al. Robust anonymous authentication protocol for health-care applications using wireless medical sensor networks[J]. Multimedia Systems, 2015, 21(1): 49-60. [本文引用:1]
[17]	Kuo T W, Lin C J, Tsai M J. On the construction of data aggregation tree with minimum energy cost in wireless sensor networks: NP-completeness and approximation algorithms[J]. IEEE Transactions on Computers, 2016, 65(10): 3109-3121. [本文引用:1]
[18]	Younis M, Akkaya K, Youssef M. Hand ling QoS traffic in wireless sensor networks[J]. IEEE Journal on Selected Areas in Communications, 2015, 28(7): 1105-1115. [本文引用:1]
[19]	Zhang J, Ren F, Gao S, et al. Dynamic routing for data integrity and delay differentiated services in wireless sensor networks[J]. IEEE Transactions on Mobile Computing, 2015, 14(2): 328-343. [本文引用:1]
[20]	Radouanelqdour, Younes, Jabrane. Wavelet networks for reducing the envelope fluctuations in Wireless Man-OFDM systems[J]. Digital Communications & Networks, 2016, 2(2): 77-83. [本文引用:1]
[21]	Doavi A, Parvan H, Salama A A, et al. Security in wireless sensor networks[J]. Communications of the ACM, 2015, 47(6): 53-57. [本文引用:1]

2014

0.0

. 2014, 31(3):100-104 DOI:doi:10.3969/j.issn.1006-9348.2014.03.023

Research and simulation of optimization method for avionics system failure detection

航电系统失效检测优化方法研究与仿真

Zhang Chao , Zhang Feng-ming , Wu Hu-sheng

张超, 张凤鸣, 吴虎胜

摘　要：研究航电系统失效准确检测的方法。航电系统有众多硬件软件组成。系统在失效后。失效信号与正常信号之间形成纠缠，造成混沌性。传统的检测方法都以在纠缠信号中分离出失效信号为基础，由于纠缠过程不能约束，并伴随混沌性，无法正确分割提取，造成检测效果不好。提出了一种基于连续模糊动态模型的航电系统失效检测方法。对航电系统失效信号在纠结衰减过程中的衰减程度进行估计，从而对其进行有效的补偿，建立连续模糊动态模型，根据模型的输出结果提取失效信号，从而完成航电系统失效检测。实验结果表明，利用改进模型进行航电系统失效检测，能够从大量的航电信号中准确提取出有效信号，提高检测的准确性。

... 0 引言无线传感网络(Wireless sensor networks,WSN)节点的工作性能影响着传感网络的工作性能^[1] ...

2016

0.0

. 2016, 46(1):327-332 DOI:doi:10.13229/j.cnki.jdxbgxb201601049

Wireless sensor network energy balance ant colony routing algorithm

无线传感器网络能量均衡蚁群路由算法

Teng Zhi-jun , Zhang Fan , Song Ming-hui.

滕志军, 张帆, 宋明辉

摘　要：针对蚁群路由算法容易形成环路及其能量分布不够均匀等问题,提出改进的蚁群路由算法。改进的算法在Hello包中增加蚂蚁标识组合项,并通过广播的方式存储到其他节点的邻居列表中,有效削弱了环路效应,同时修正信息素更新公式,提升多节点区域信息素更新的准确性,并引入能量差异因子,将能量差异因子作为信息素浓度更新的参考因素,改善了网络节点能量分布不均的问题,获得了更好的平衡。仿真结果表明改进算法可有效削弱环路效应并更好地均衡网络节点能量。

... 一旦WSN在部分区域发生失效或者均衡性改变,会对相关生产安全带来无法想象的灾难^[2] ...

2015

0.0

... 文献[3]提出通过层次分析法评估WSN性能,但是该方法是基于专家打分的方式实现评估,主观性较高 ...

2015

0.0

... 文献[4]基于层次分析法获取网络安全参数特征的权重,同样主观性较强 ...

2014

0.0

. 2014, 44(4):1191-1196 DOI:doi:10.13229/j.cnki.jdxbgxb201404044

Self-adaptive Monte Carlo localization algorithm of mobile nodes in WSN

自适应蒙特卡罗无线传感器网络移动节点定位算法

Li Jian-po , Shi Ming , Zhong Xin-xin.

李建坡, 时明, 钟鑫鑫

摘　要：针对无线传感器网络中蒙特卡罗定位算法在节点的无线射程为非理想条件下定位精度不高、采样率低等缺点，提出一种自适应蒙特卡罗移动节点定位算法。该算法利用不同区域的采样粒子对未知节点的定位精度影响不同，自适应地调整不同区域的采样粒子的影响权重，对未知节点进行定位；同时，利用上一时刻采样粒子增加限定条件，提高定位精度。仿真结果表明，本算法在规则度不同的条件下节点的定位误差平均下降了约13％，在速度不同的条件下定位误差平均下降了约10％，网络覆盖率可达到99．19％。

... 文献[5]只对3个获取属性权重的算法进行了分析,但是未分析这些方法的实际应用过程 ...

2016

0.0

. 2016, 46(3):876-883 DOI:doi:10.13229/j.cnki.jdxbgxb201603030

Cluster size adaptive adjustable strategy for wireless sensor networks

无线传感器网络簇半径自适应调整策略

Zhang Jing , Liu Yan-heng , Zhang Jin-dong.

张婧, 刘衍珩, 张晋东

摘　要：首先,基于节点的剩余能量对节点簇半径进行周期性调整,将网络划分为大小非均匀的若干簇。其次,设计了簇头选举策略,使得网络中簇头分布更加合理,提升簇头节点能量利用率,均衡节点的能耗。实验结果表明：与UCR算法和CUCRA算法相比,本文提出的算法将网络生命周期分别延长了55.2%和38.2%,同时具有较低的传输延时。

... 文献[6]对比分析了几种定位算法,但是未对实际应用过程进行验证,缺少客观性 ...

2015

0.0

... 文献[7]通过随机Petri网评价面向WSN结构的安全性能,这种方法需要大量的先验知识作为支撑条件,限制了其应用 ...

2015

0.0

... 文献[8]提出了针对WSN组合安全性能和可靠性瓶颈进行闭环分析的随机方法,但是由于引入了多模型,模型之间没有统一的衡量标准,导致检测目标不明确 ...

2014

0.0

. 2014, 22(4):1012-1019

Detection of salient maps by fusion of contrast and distribution

融合对比度和分布性的图像显著性区域检测

Zhang Ying-ying , Zhang Shuai , Zhang Ping.

张颖颖, 张帅, 张萍

... 文献[9]在环境监测中使用(Unified modeling language,UML)表示WSN安全分析模型,将结构图、故障树以及马尔可夫模型融入该模型,实现了模型的自主映射,进而研究了传感网络安全性检测的有效性 ...

2016

0.0

. 2016, 42(8):39-45

Low-power wireless sensing technology and its application based on queuing theory

基于排队论的低功耗无线传感技术及其应用

Wang Zhi-fan , Ye Qing-wei , Zhou Yu

王志繁, 叶庆卫, 周宇

... 文献[10]通过排队方法对WSN软、硬件失效状态时的多层模块安全性进行分析,该方法采用的排队网是一种乘积网,具有一定的局限性 ...

2017

0.0

. 2017, 25(5):1312-1321 DOI:doi:10.3788/OPE.20172505.1312

Salient subtle region accurate detection via cellular automata multi-scale optimization

元胞自动机多尺度优化的显著性细微区域检测

Xu Tao , Jia Song-min , Zhang Guo-liang.

徐涛, 贾松敏, 张国梁

针对由于待检测目标局部区域显著性差异过大造成的细微区域检测失败问题，在贝叶斯理论框架下，提出一种基于元胞自动机多尺度优化的显著性检测方法。首先结合暗通道先验信息和区域对比度在同一张图片的5个超像素尺度空间内分别构建原始显著性图；接着，利用元胞自动机建立动态更新机制，通过影响因子矩阵和置信度矩阵优化每个元胞下一状态的影响力，获得对应5个优化显著性图；最后在基于贝叶斯理论的融合算法框架下得到最终的显著性图。在两个复杂度不同的标准图像数据库上将本文方法与10种主流显著性提取方法进行视觉效果和客观定量数据对比，结果显示，本文算法效果优于现有10种显著性提取方法，其中在公认最具挑战的DUT-OMRON数据库的综合指标-measure值为0.631 4，平均绝对误差（MAE）为0.132 5，ROC曲线下面积（AUC）为0.892 8，表明本文算法具有较高的准确性和鲁棒性。

... 文献[11]在检测WSN稳定性和安全性时,采用比特错误率的观点分析网络全部任务的运行状态、服务间的状态转移过程以及网络工作的环境,进而定量分析网络的失效过程 ...

2016

0.0

. 2016, (4):84-86

Fault detection algorithm for wireless sensor networks based on hybrid immune system mechanism

基于混合免疫系统机理的无线传感网络故障检测算法

Wang Ming-wei , Chen Li-wan , Li Hong-bing

王明伟, 陈立万, 李洪兵

... 文献[12,13]采用混合免疫方法改进错误率干扰下的WSN测试性能,但是该种方法耗时严重 ...

2014

0.0

. 2014, 27(5):658-663 DOI:doi:10.3969/j.issn.1004-1699.2014.05.017

Wireless sensor networks node fault diagnosis based on immune danger theory

基于免疫危险理论的无线传感器网络节点故障诊断

Zhao Xi-heng , He Xiao-min , Xu Liang

赵锡恒, 何小敏, 许亮

针对无线传感器网络的故障特点以及故障诊断的自学习问题,本文提出一种基于免疫危险理论的无线传感器网络节点故障诊断算法。该方法利用危险触发阈值来识别危险源,用遗传算法生成抗体库,基于K近邻分类法构建多抗体故障检测器并进行故障分类,通过追踪故障数据变化更新抗体库。实验仿真证明,该算法与其他无线传感器网络故障诊断算法相比,在训练数据较少的情况下,诊断准确率更高,效率更好,耗用硬件计算资源更少,并具备动态更新特性。

... 文献[12,13]采用混合免疫方法改进错误率干扰下的WSN测试性能,但是该种方法耗时严重 ...

2015

0.0

. 2015, 38(3):625-647 DOI:doi:10.3724/SP.J.1016.2015.00625

Survey on invulnerability of wireless sensor networks

无线传感器网络抗毁性

Li Wen-feng , Fu Xiu-wen.

李文锋, 符修文

无线传感器网络常因能量耗尽、硬件故障或者遭遇入侵等原因导致节点失效,使得原本连通的网络拓扑分割,甚至导致全局网络受损.因此,研究抗毁性对解决无线传感器网络规模化应用瓶颈具有重要的理论价值.目前有关无线传感器网络抗毁性的研究主要关注以下3个方面:(1)造成无线传感器网络节点失效与网络受损的原因有哪些;(2)如何准确度量无线传感器网络抗毁性;(3)如何有效提升无线传感器网络抗毁性能.文中有针对性地分别从失效成因、测度、提升策略与故障检测和修复等4个方面对有关研究进行归纳和分类,重点分析无线传感器网络抗毁性优化方法,包括路由控制、网络重构和拓扑演化.最后,指出无线传感器网络抗毁性研究未来发展所面临的技术挑战,并就其发展趋势进行探讨.

... 伪随机过程在数学上可以用一种蝴蝶效应性来描述,使得WSN在失效前期,存在一定蝴蝶抗毁性效应^[14],原因如下: ...

2015

0.0

. 2015, 8(5):768-774

A saliency target area detection method of image sequence

图像序列的显著性目标区域检测方法

Ke Hong-chang , Sun Hong-bin.

柯洪昌, 孙宏彬

... 图1为WSN出现访问篡改失效下,通过Matlab完成对获取的失效节点的Lyapunov指数图仿真^[15] ...

2015

0.0

... 通过寻求网络失效节点蝴蝶效应特征,分析WSN在失效早期的节点特征、内在变化规律及内部关系,在非线性时间序列中寻找能反映网络软件和硬件失效特征的蝴蝶效应节点特征关联^[16],进行相应的特征提取,可以有效地形成失效判断,方法如下:以节点分类器为依据,将WSN失效后,节点分类中的误码率变换为一系列概率密度函数,以这一系列密度函数为依据,分配不同的使用概率 ...

2016

0.0

... 在给定的重构映射 m维相空间内,产生 m维矢量,利用式(1)表述^[17]: ...

2015

0.0

2015

0.0

... (2)运用MRF(Multiple reference frames)方法^[19]通过先验分布模型对蝴蝶效应问题的解作某种约束,通过样条函数作平滑约束,可以保证蝴蝶效应中的对偶都是唯一解 ...

2016

0.0

... 1 试验环境设计QPME(Queuing petri net modeling environ-ment)软件包是一款利用QPN特性的建模工具,仿真试验结果表明,利用QPME建模工具能够较好地反映和预测WSN的性能变化^[20,21] ...

2015

0.0