相干/同向信号波达方向与多普勒频率的联合估计

引用本文

单泽彪, 刘小松, 王春阳, 石屹然, 石要武. 相干/同向信号波达方向与多普勒频率的联合估计[J].吉林大学学报（工学版）, 2017,47(6): 1949-1956
SHAN Ze-biao, LIU Xiao-song, WANG Chun-yang, SHI Yi-ran, SHI Yao-wu. Joint estimation of DOA and Doppler frequency for coherence and/or same-direction signals[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1949-1956 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706037
Permissions

相干/同向信号波达方向与多普勒频率的联合估计

单泽彪^1,², 刘小松¹, 王春阳¹, 石屹然², 石要武²

1.长春理工大学电子信息工程学院,长春 130022

2.吉林大学通信工程学院,长春 130022

通讯作者:刘小松(1988-),女,讲师,博士.研究方向:信息处理与先进控制技术.E-mail:liuxiaosong9@163.com

作者简介:单泽彪(1986-),男,讲师,博士.研究方向:光电检测与现代信号处理.E-mail:zbshan@126.com

基金:国防基础科研计划项目(JCKY2016411C006); 国家自然科学基金项目(61571462)

摘要

针对相干/同向信号波达方向(DOA)与多普勒频率的联合估计问题,提出了一种基于特征空间的修正二维MUSIC联合估计算法。首先,建立包含DOA和多普勒频率信息的广义阵列信号模型,通过共轭重构对阵列接收信号的协方差矩阵进行修正,使其有效适用于相干/同向信号下DOA与多普勒频率的联合估计。同时,在二维MUSIC算法的基础上,提出了一种基于特征空间的DOA与多普勒频率联合估计算法,该算法充分利用了信号子空间和噪声子空间的信息,并且可以对源信号功率进行估计。对该算法加以修正后同样可以应用于相干/同向信号的DOA与多普勒频率联合估计,且可以得到比修正二维MUSIC算法更好的估计效果。最后,通过仿真试验验证了本文算法的有效性。

关键词: 信息处理技术; 波达方向估计; 多普勒频率估计; 相干信号; 同向信号; 信号功率估计

中图分类号:TN91 文献标志码:A 文章编号:1671-5497(2017)06-1949-08

Joint estimation of DOA and Doppler frequency for coherence and/or same-direction signals

SHAN Ze-biao^1,², LIU Xiao-song¹, WANG Chun-yang¹, SHI Yi-ran², SHI Yao-wu²

1.School of Electronic and Information Engineering, Changchun University of Science and Technology, Changchun 130022,China

2.College of Communication Engineering, Jilin University, Changchun 130022, China

Abstract

This paper is concerned with the joint estimation problem of Directions of Arrival (DOAs) and Doppler Frequency (DF) for coherence and/or same-direction signals. An eigen-space based modified 2D-MUSIC algorithm is proposed. First, a generalized array signal model is established, which incorporates both DOAs and DFs information. Then, the covariance matrix of the received signals of antenna array is modified through conjugate reconstruction to make it applicable for joint estimation of DOAs and DFs for coherence and/or same-direction signals. On the basis of 2D-MUSIC algorithm, an eigen-space based algorithm for joint estimation of DOAs and DFs is presented, where the information of both signal and noise subspaces is utilized, and this algorithm can estimate the signal power as well. Besides, a modified eigen-space algorithm is given, which can also implement joint estimation of DOAs and DFs for coherence and/or same-direction signals, and it is superior to the modified 2D-MUSIC algorithm in term of estimation performance. Several contrastive simulation results are presented to elucidate the validity of the proposed algorithms.

Keyword: information procession technology; directions of arrival (DOA) estimation; Doppler frequency estimation; coherent signals; same-direction signals; signal power estimation

Show Figures

0 引言

DOA与多普勒频率联合估计一直都是雷达、声纳、无线通信和地震勘探等领域中的研究热点。针对DOA与多普勒频率的联合估计, 人们已经提出了诸多研究方法, 如线性预测算法、最大似然方法、ESPRIT类算法、MUSIC类算法以及基于压缩感知的估计方法等。尽管最大似然方法^{[1, 2]}是一种最优估计方法, 但其需要多维穷尽搜索, 应用常规搜索方法计算量巨大。Lemma等^[3]基于一维ESPRIT算法提出了一种联合角度与频率估计(JAFE)方法, 该方法在有效降低计算量的同时仍具有较高的估计精度, 但是其估计参数无法自动配对。Lin等^[4]在无线通信领域中基于MUSIC算法提出了一种用于DOA与频率联合估计的FSF-MUSIC算法, 该算法在具体运算过程中需要通过两次一维频率估计和一次一维角度估计来实现联合估计。张志成等^[5]通过状态空间模型建立了包含DOA和多普勒频率两者信息的广义可观测矩阵, 结合二维MUSIC算法及隔离小生境混合蛙跳方法实现了DOA与多普勒频率的联合估计。赵曼等^[6]针对宽频段信号角度与频率联合估计的欠采样问题, 给出了一种基于扩维的联合估计算法。然而, 上述方法的适用条件均为非相关信号情况下, 当信号高度相关或相干时, 它们的性能将严重恶化甚至失效。

针对多径传播环境中相干信号的DOA与多普勒频率联合估计问题, 文献[7]利用空间平滑预处理技术, 通过构造时-空平滑数据矩阵实现了相干信号DOA与频率的联合估计, 但是文献[7]仅利用了前向空间平滑技术, 而忽略了与后向空间平滑技术的综合运用, 以至于在阵元数较少的情况下估计精度相对较差。为了提高阵元的利用率, 文献[8]在文献[7]的基础上, 结合前、后向空间平滑技术给出了一种相干信号联合波达角及频率估计的预处理方法, 较大程度地提高了参数的估计性能。杜刚等^{[9, 10]}同样利用空间平滑技术并结合双平行线阵的时空数据结构, 实现了空间相干信号的频率及二维波达方向的估计。文献[11, 12]利用空间信号本身存在的稀疏特性, 结合压缩感知理论研究了DOA与频率的联合估计问题。但是, 上述算法均未考虑到同向信号源存在时的参数估计问题, 并且利用空间平滑技术解相干会带来阵列孔径的损失。

为了进一步提高阵列的有效孔径, 解决同向信号存在时的参数估计问题, 本文提出了一种利用数据共轭重构的修正二维MUSIC(2D-MMUSIC)算法, 该算法在不影响非相关信号参数估计的前提下, 可有效估计相干/同向信号的DOA和多普勒频率, 且无阵列孔径的损失。同时, 针对传统二维MUSIC算法仅利用单一噪声子空间, 而丢掉信号子空间信息的问题, 提出了一种基于特征空间的二维MUSIC(2D-ES-MUSIC)算法, 使其最大限度地利用噪声子空间和信号子空间的信息。本文提出的2D-ES-MUSIC算法还可以对源信号的功率进行有效估计, 并保留参数自动配对的优点。此外, 修正特征空间二维MUSIC(2D-ES-MMUSIC)算法后, 同样可以将其应用于相干/同向信号存在时的情况, 而且可以得到比2D-MMUSIC算法更好的估计效果。

1 阵列信号数学模型

1.1 接收数据模型

假设有K个中心频率均为f_c的远场窄带信号入射到一个由D(D> K)个全向天线构成的阵元间隔均为d的均匀线阵上, 考虑信源运动导致多普勒频率存在的情况下, 各信号的多普勒频率分别为f_k(k=1, 2, …, K), 则每个阵元接收到的信号可表示为^[5]:

$\begin{matrix} \begin{matrix} x_{i} (t) = \overset{K}{\sum_{k = 1}} a_{i} (θ_{k}) s_{k} (t) + g_{i} (t) (1) \\ i = 1, 2, \dots, D \end{matrix} \end{matrix}$

式中:a_i(θ _k)=exp[-j2π f_cd(i-1)sinθ _k/c], θ _k为第k个信源的波达方向; s_k(t)=u_kexp(j2π f_kt), u_k为复幅度; g_i(t)为加性零均值高斯白噪声。

式(1)可表示为如下向量形式:

$x (t) = \overset{K}{\sum_{k = 1}} a (θ_{k}) s_{k} (t) + g (t) (2)$

式中：

$x (t) = {[x_{1} (t), x_{2} (t), \dots, x_{D} (t)]}^{T} (3)$

$a (θ_{k}) = {[a_{1} (θ_{k}), a_{2} (θ_{k}), \dots, a_{D} (θ_{k})]}^{T} (4)$

$g (t) = {[g_{1} (t), g_{2} (t), \dots, g_{D} (t)]}^{T} (5)$

进而得到如下空时信号模型:

$s (t + 1) = Φs (t) (6)$

$x (t) = As (t) + g (t) (7)$

式中：

$A = [a (θ_{1}), a (θ_{2}), \dots, a (θ_{K})] (8)$

$s (t) = {[s_{1} (t), s_{2} (t), \dots, s_{K} (t)]}^{T} (9)$

$Φ = diag [e^{j ω_{1}}, e^{j ω_{2}}, \dots, e^{j ω_{K}}] (10)$

式中:ω _k=2π f_k; k=1, 2, …, K。

构造接收数据矩阵x和噪声数据矩阵g的Hankel矩阵如式(11)和(12)所示:

$X = [\begin{matrix} x (0) & x (1) & \dots & x (N - 1) \\ x (1) & x (2) & \dots & x (N) \\ ︙ & ︙ & ︙ \\ x (M - 1) & x (M) & \dots & x (M + N - 1) \end{matrix}] (11)$

$G = [\begin{matrix} g (0) & g (1) & \dots & g (N - 1) \\ g (1) & g (2) & \dots & g (N) \\ ︙ & ︙ & ︙ \\ g (M - 1) & g (M) & \dots & g (M + N - 1) \end{matrix}] (12)$

式中:M和N分别为Hankle矩阵的行数和列数, M+N为采样快拍数。

定义一种信号采样序列如下所示:

$\begin{matrix} S = [s (0), s (1), \dots, s (N - 1)] (13) \end{matrix}$

则得到一种广义的阵列接收信号模型:

$\begin{matrix} X = Γ_{M} S + G (14) \end{matrix}$

式中:Γ _M= $\begin{matrix} {[A^{T}, {(AΦ)}^{T}, \dots, {(A Φ^{M - 1})}^{T}]}^{T} \end{matrix}$ 为一种广义阵列流形矩阵, 其中包含了待估计的DOA和多普勒频率。

把矩阵X的每一列看作一次采样, 则式(14)可写为如下形式:

$\begin{matrix} \begin{matrix} X (n) = Γ_{M} S (n) + G (n) (15) \\ n = 0, 1, \dots, N - 1 \end{matrix} \end{matrix}$

1.2 相干信号模型

由于复杂环境中多径传播等因素的影响, 在实际通信系统中强相关或相干信号是普遍存在的。考虑K个相干信号源, 则每个信号均可以用同一个信号表示, 即:

$\begin{matrix} s_{i} (t) = α_{i} s (t), i = 1, 2, \dots, K (16) \end{matrix}$

式中:s表示生成信号; α _i表示第i个信号相对于s的增益。

联合式(9), 将式(16)代入式(7)中, 得到相干信号的阵列接收信号模型:

$\begin{matrix} x (t) = Aαs (t) + g (t) (17) \end{matrix}$

式中:α = $\begin{matrix} {[α_{1}, α_{2}, \dots, α_{K}]}^{T} \end{matrix}$ 。

1.3 同向信号模型

复杂多变的环境中, 两个信号源处于同一波达方向上或相距较近, 其DOA无法分辨时, 它们的DOA即可认为是相同的, 称这种情况为同向源信号。假设存在K个同向源信号, 即θ _i=θ (i=1, 2, …, K), 则有:

$\begin{matrix} a (θ_{i}) = a (θ), i = 1, 2, \dots, K (18) \end{matrix}$

将式(8)(18)代入式(7)中, 得到同向信号的阵列接收信号模型为:

$\begin{matrix} x (t) = βa (θ) s (t) + g (t) (19) \end{matrix}$

式中:β =为1× K维全1向量。

2 本文算法描述

2.1 修正二维MUSIC算法

在得到广义阵列接收信号模型式(15)后, 可求得X的协方差矩阵为:

$\begin{matrix} R_{X} = E [X (n) X^{H} (n)] = Γ_{M} R_{S} {Γ^{H}}_{M} + σ^{2} I (20) \end{matrix}$

式中:(· )^H表示共轭转置; R_S=E $\begin{matrix} [S (n) S^{H} (n)] \end{matrix}$ 为信号协方差矩阵; σ ²为噪声方差; I为单位阵。

对R_X进行特征值分解, 有:

$\begin{matrix} R_{X} = U_{XS} Σ_{XS} {U^{H}}_{XS} + U_{XG} Σ_{XG} {U^{H}}_{XG} (21) \end{matrix}$

式中:U_XS和U_XG分别为信号子空间和噪声子空间; Σ _XS和Σ _XG分别为较大特征值和较小特征值所构成的对角阵。

由于G为高斯白噪声向量, 所以噪声方差可由式(22)进行估计:

$\begin{matrix} {\hat{σ}}^{2} = tr (Σ_{XG}) / (MD - K) (22) \end{matrix}$

式中:tr为矩阵求迹运算。

信号子空间正交于噪声子空间, 阵列流形Γ _M中的导向矢量同样正交于噪声子空间, 所以DOA与多普勒频率联合估计的二维MUSIC空间谱函数可表示为^[5]:

$\begin{matrix} P_{MUSIC} (θ, ω) = \frac{1}{{Γ^{H}}_{M} (θ, ω) U_{XG} {U^{H}}_{XG} Γ_{M} (θ, ω)} (23) \end{matrix}$

通过式(23)进行谱峰搜索, 即可求得DOA和多普勒频率的估计值。然而在源信号相干或同向的情况下, 二维MUSIC算法性能将严重下降甚至失效。针对该问题, 本文提出了一种利用数据共轭重构的相干/同向信号DOA与多普勒频率联合估计的2D-MMUSIC算法。

定义一个MD× MD维反单位矩阵J, 即:

$\begin{matrix} J = [\begin{matrix} 0 & \dots & 0 & 1 \\ ︙ & ⋰ & 1 & 0 \\ 0 & ⋰ & ⋰ & ︙ \\ 1 & 0 & \dots & 0 \end{matrix}] (24) \end{matrix}$

并利用J对接收数据矩阵X进行变换:

$\begin{matrix} Y (l) = J X^{*} (l) (25) \end{matrix}$

式中:(· )^*表示复共轭。

Y(l)的协方差矩阵可表示为:

$\begin{matrix} \begin{matrix} R_{Y} = E [Y (l) Y^{H} (l)] = \\ J Γ_{M}^{*} R_{S}^{*} {Γ^{T}}_{M} J + σ^{2} I = J R_{X}^{*} J (26) \end{matrix} \end{matrix}$

联合式(20)(26), 得重构后的协方差矩阵为:

$\begin{matrix} R = \frac{R_{X} + R_{Y}}{2} = \frac{R_{X} + J R_{X}^{*} J}{2} (27) \end{matrix}$

当存在相干/同向源信号时, R_X仅为Hermite矩阵, 而将R_X按式(27)修正后所得的R为Toeplitz矩阵。因此, 用R代替R_X进行特征分解便可解决相干或同向源信号存在情况下的参数估计问题。在实际应用中, R_X是在有限次快拍且含噪情况下估计所得, 因此, 用R_X和R_Y的平均值R进行DOA与多普勒频率联合估计, 可以进一步提高算法的估计性能, 这是本文修正算法带来的又一个优势。另外, 修正后的协方差矩阵R也同样适用于非相关信号DOA与多普勒频率的联合估计。

2.2 基于特征空间的二维MUSIC算法

考虑传统2D-MUSIC算法仅利用噪声子空间, 而忽略了信号子空间信息的问题, 提出了一种用于DOA与多普勒频率联合估计的2D-ES-MUSIC算法, 该算法充分利用了信号子空间和噪声子空间两者的信息。

定义矩阵:

$\begin{matrix} R_{A} = Γ_{M} R_{S} {Γ^{H}}_{M} = U_{XS} (Σ_{XS} - σ^{2} I) {U^{H}}_{XS} (28) \end{matrix}$

单取第k个信号的导向矢量, 进一步计算可得:

$\begin{matrix} \begin{matrix} {Γ^{H}}_{M} (θ_{k}, ω_{k}) R_{A}^{+} Γ_{M} (θ_{k}, ω_{k}) = \\ {Γ^{H}}_{M} (θ_{k}, ω_{k}) {(Γ_{M} R_{S} {Γ^{H}}_{M})}^{+} Γ_{M} (θ_{k}, ω_{k}) = \\ {[Γ_{M}^{+} Γ_{M} (θ_{k}, ω_{k})]}^{H} R_{S}^{+} Γ_{M}^{+} Γ_{M} (θ_{k}, ω_{k}) = \\ {δ^{T}}_{k} R_{S}^{+} δ_{k} = {[R_{S}^{+}]}_{k, k} = 1 / p_{k} (29) \end{matrix} \end{matrix}$

式中:(· )⁺表示求伪逆运算; δ _k=[0, …, 0, 1, 0, …, 0]^T为第k个元素为1其余均为0的K× 1维向量; p_k为第k个信号的功率。

因此, 可以得到一种新的联合谱函数:

$\begin{matrix} P_{ES - MUSIC} (θ, ω) = \frac{{Γ^{H}}_{M} (θ, ω) R_{A}^{+} Γ_{M} (θ, ω)}{{Γ^{H}}_{M} (θ, ω) U_{XG} {U^{H}}_{XG} Γ_{M} (θ, ω)} (30) \end{matrix}$

对式(30)联合谱函数进行谱峰搜索, 当θ =θ _k, 且ω =ω _k时, U_XG $\begin{matrix} {U^{H}}_{XG} \end{matrix}$ Γ _M=0, 而Γ _M=1/p_k, 则P_ES-MUSIC(θ , ω )联合空间谱函数在θ =θ _k, ω =ω _k, k=1, 2, …, K处出现谱峰。因此, 可以利用P_ES-MUSIC进行DOA与多普勒频率的联合估计。同时为了保证在相干/同向信号情况下也能有效估计DOA及多普勒频率, 可以预先对接收信号协方差矩阵按照式(27)进行重构。另外, 利用式(29)还可以对源信号功率进行估计, 便于对小能量信号或相干且同向信号的检测判断。

3 仿真验证及结果分析

为了对本文算法的性能进行有效性验证及对比分析, 分别在非相关、相干、同向和相干同向4种情况下进行有关试验。试验中, 均假设信号源数目已知或已正确估计得到, 试验中采用10阵元且阵元间隔均为半波长的均匀线阵列, 设置蒙特卡罗独立试验次数为1000, 快拍数为100。采用归一化频率来描述多普勒频率, 则DOA和多普勒频率的成功估计概率分别定义为估计所得偏差小于或等于1° 或0.1 rad时次数的比例。所有参数(DOA、多普勒频率或功率)估计的均方根误差(RMSE)表示为:

$\begin{matrix} RMSE = \sqrt[]{\frac{1}{1000 K} \overset{K}{\sum_{k = 1}} \overset{1000}{\sum_{q = 1}} {[{\hat{ϑ}}_{k} (q) - ϑ_{k}]}^{2}} (31) \end{matrix}$

式中:K为信号源数目; $\begin{matrix} {\hat{ϑ}}_{k} \end{matrix}$ 为第q次第k个信源参数的估计值; ϑ _k为第k个信源参数的真实值。

试验1 有效性验证试验。针对上述4种情况下DOA与多普勒频率联合估计问题, 分别对2D-MUSIC算法、2D-ES-MUSIC算法、2D-MMUSIC算法和2D-ES-MMUSIC算法4种算法进行仿真验证。试验条件分别为:

(1)非相关:信号源数目为2; 信号功率分别为1.0和0.8 W; DOA分别为30° 和-30° ; 归一化频率分别为1和1.5 rad。

(2)相干:信号源数目为2; 信号功率分别为1.0和0.8 W; DOA分别为30° 和-30° ; 归一化频率均为1 rad。

(3)同向:信号源数目为2; 信号功率分别为1.0和0.8 W; DOA均为30° ; 归一化频率分别为1和1.5 rad。

(4)相干同向:信号源数目为3; 信号功率分别为1.0、0.9和0.8 W; DOA分别为30° 、30° 和-30° ; 归一化频率分别为1、1.5和1.5 rad。

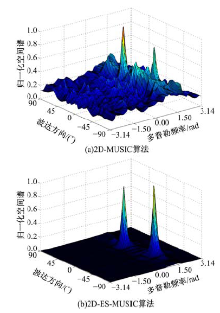
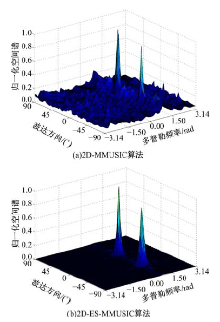
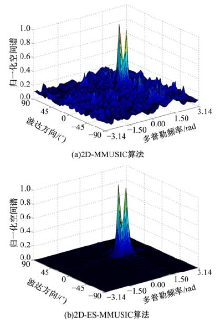
当信噪比为-10 dB时, 分别给出了上述4种情况下4种算法的空间谱如图1~图4所示。

	Figure Option View Download New Window
	图1 非相关信号DOA与多普勒频率联合估计Fig.1 Joint estimation DOAs and Doppler frequencies for uncorrelated signals

	Figure Option View Download New Window
	图2 相干信号DOA与多普勒频率联合估计Fig.2 Joint estimation DOAs and Doppler frequencies for correlated signals

	Figure Option View Download New Window
	图3 同向信号DOA与多普勒频率联合估计Fig.3 Joint estimation DOAs and Doppler frequencies for same-direction signals

	Figure Option View Download New Window
	图4 相干同向信号DOA与多普勒频率联合估计Fig.4 Joint estimation DOAs and Doppler frequencies for coherent and/or same-direction signals

从图1中可以看出, 在非相关条件下, 本文2D-ES-MUSIC算法的性能明显优于传统2D-MUSIC算法, 其表现为谱峰更加尖锐, 旁瓣更小, 伪峰更少。这主要是因为本文算法充分利用了信号和噪声两个子空间的信息, 对噪声具有较强的抑制能力。从图2~图4中可以看出, 在相干/同向信号条件下, 2D-MMUSIC算法和2D-ES-MMUSIC算法均可以对DOA及多普勒频率进行有效估计, 这说明本文修正算法是有效的。并且与2D-MMUSIC算法相比, 2D-ES-MMUSIC算法具有更好的估计性能, 其表现同样为谱峰更加尖锐, 谱宽更窄, 伪峰更少。

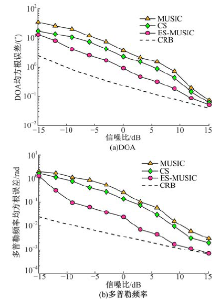
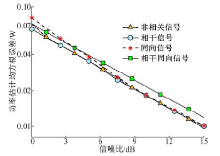
试验2 与其他算法的估计性能对比试验。针对试验1中所描述的非相关信号情况, 验证本文2D-ES-MUSIC算法在不同信噪比条件下的估计性能, 并且与2D-MUSIC算法以及基于压缩感知(CS)的联合估计方法进行比较。图5(a)(b)分别给出了上述3种算法在不同信噪比条件下的DOA与多普勒频率联合估计的均方根误差及相应的克拉美罗界(CRB)^[9]。从图中可以看出:在不同信噪比时, 2D-ES-MUSIC算法具有最小的均方根误差, 说明2D-ES-MUSIC算法具有比另外两种算法更好的估计性能。

	Figure Option View Download New Window
	图5 非相关信号条件下的算法性能比较Fig.5 Performance comparison of different algorithms for uncorrelated signals

	Figure Option View Download New Window
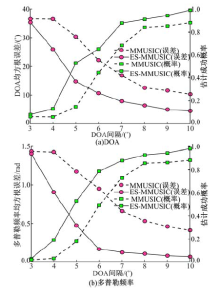	图6 相干信号不同DOA间隔条件下的均方根误差与估计成功概率Fig.6 RMSE and resolution probability for correlated signals versus different DOA intervals

试验3 分辨力验证试验。针对2D-MMUSIC算法和2D-ES-MMUSIC算法, 在信噪比为0dB时, 分别通过以下两个试验验证所提算法的估计性能与分辨力。一个是相干信号不同DOA间隔条件下的DOA与多普勒频率联合估计均方根误差及估计成功概率试验; 另一个是同向信号不同多普勒频率间隔条件下的DOA与多普勒频率联合估计均方根误差及估计成功概率试验, 试验结果分别如图6(a)(b)、图7(a)(b)所示。从图6(a)(b)中可以看出:在相干信号条件下, 2D-ES-MMUSIC算法比2D-MMUSIC算法具有更低的均方根误差和更高的估计成功概率, 说明2D-ES-MMUSIC算法具有更好的估计性能以及更高的分辨力, 并且其分辨力随着DOA间隔的增大而逐渐变好。从图7(a)(b)中可以看出:在同向信号条件下, 也具有与相干信号条件下相似的结论, 即2D-ES-MMUSIC算法比2D-MMUSIC算法具有更好的估计性能。

	Figure Option View Download New Window
	图7 同向信号不同多普勒频率间隔条件下的均方根误差与估计成功概率Fig.7 RMSE and resolution probability for same-direction signals versus different Doppler frequencies intervals

试验4 鲁棒性验证试验。为了进一步验证本文算法的稳健性和鲁棒性, 针对试验1中所描述的相干、同向和相干同向3种情况, 分别给出了不同信噪比下DOA与多普勒频率联合估计的均方根误差及相应的克拉美罗界(CRB), 如图8(a)(b)所示。从图中可以看出, 针对以上3种情况, 在不同信噪比条件下, 2D-ES-MMUSIC算法均具有比2D-MMUSIC算法更高的估计精度, 且更早地贴近CRB, 说明前者比后者具有更高的算法稳健性和抗噪鲁棒性, 并且它们的估计性能均随信噪比的不断增大而逐渐变好。

试验5 信号功率估计试验。针对试验1中所描述的非相关、相干、同向和相干同向4种情况, 利用文中算法对源信号的功率进行估计。图9为不同信噪比条件下的功率估计均方根误差, 从图9中可以看出, 本文算法在不同情况下均具有较好的功率估计性能。在信噪比为0 dB时, 4种情况下功率估计的均方根

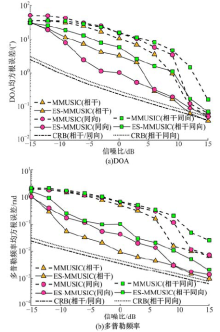	Figure Option View Download New Window
	图8 相干/同向信号条件下的算法性能比较Fig.8 Performance comparison of different algorithms for coherent and/or same-direction signals

	Figure Option View Download New Window
	图9 不同信噪比时功率估计均方根误差Fig.9 RMSE of signals power estimation versus SNR

误差均要小于0.1 W, 并且随着信噪比的增加功率估计的均方根误差逐渐减小。

4 结束语

针对相干/同向信号DOA与多普勒频率的联合估计问题, 首先在传统2D-MUSIC算法的基础上提出了一种利用数据共轭重构的2D-MMUSIC算法, 该算法在信号相干、同向或相干同向三种情况下均能有效估计信号DOA及多普勒频率, 并且不影响非相关信号时DOA与多普勒频率的估计。同时, 根据2D-(M)MUSIC算法仅利用单一噪声子空间而忽略信号子空间的问题, 提出了一种基于特征空间的2D-ES-(M)MUSIC算法, 该算法充分利用了噪声子空间和信号子空间两者的信息。仿真结果表明:在非相干/非同向信号情况下, 2D-ES-MUSIC算法优于传统2D-MUSIC算法; 在相干/同向信号情况下, 2D-ES-MMUSIC算法优于2D-MMUSIC算法。另外2D-ES-(M)MUSIC算法还可以对源信号的功率进行有效估计, 且所估计参数均可自动配对。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	单泽彪, 石要武, 刘小松, 等. 时变遗忘因子动态DOA跟踪算法[J]. 吉林大学学报: 工学版, 2016, 46(2): 632-638. Shan Ze-biao, Shi Yao-wu, Liu Xiao-song, et al. DOA tracking algorithm of moving targets with variable forgetting factor[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(2): 632-638. [本文引用:1]
[2]	单泽彪, 石要武, 单泽涛, 等. 应用序列二次规划的波达方向与多普勒频率联合估计[J]. 光学精密工程, 2015, 23(7): 2079-2085. Shan Ze-biao, Shi Yao-wu, Shan Ze-tao, et al. Joint estimation of DOA and Doppler frequency by SQP[J]. Optics and Precision Engineering, 2015, 23(7): 2079-2085. [本文引用:1]
[3]	Lemma A N, van der Veen A J, Deprettere E F. Joint angle-frequency estimation using multi-resolution esprit[C]//Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, Seattle, WA, USA, 1998: 1957-1960. [本文引用:1]
[4]	Lin J D, Fang W H, Wang Y Y, et al. FSF MUSIC for joint DOA and frequency estimation and its performance analysis[J]. IEEE Transactions on Signal Processing, 2006, 54(12): 4529-4542. [本文引用:1]
[5]	张志成, 温炎, 石要武. 利用隔离小生境混合蛙跳方法联合估计波达方向和多普勒频率[J]. 光学精密工程, 2014, 22(9): 2565-2571. Zhang Zhi-cheng, Wen Yan, Shi Yao-wu. Joint estimation of DOAs and Doppler frequency using isolation niche shuffled frog leaping algorithm[J]. Optics and Precision Engineering, 2014, 22(9): 2565-2571. [本文引用:3]
[6]	赵曼, 陈辉. 基于扩维的多通道联合频率和到达角估计[J]. 电子与信息学报, 2014, 36(1): 147-151. Zhao Man, Chen Hui. Multichannel joint frequency and DOA estimation based on expand ed dimension[J]. Journal of Electronics and Information Technology, 2014, 36(1): 147-151. [本文引用:1]
[7]	Lemma A N, van der Veen A J, Deprettere E F. Analysis of joint angle-frequency estimation using ESPRIT[J]. IEEE Trans Signal Procession, 2003, 51(5): 1264-1283. [本文引用:3]
[8]	Yi H, Zhou X, Liu J. Forward-backward spatio-temporal smoothing for joint angle-frequency estimation in multipath environment[J]. Electronics Letters, 2003, 39(6): 574-575. [本文引用:1]
[9]	杜刚, 王永良, 张永顺, 等. 空间相干信号的频率和二维到达角估计算法[J]. 系统工程与电子技术, 2008, 30(6): 1050-1053. Du Gang, Wang Yong-liang, Zhang Yong-shun, et al. Estimation of both the frequency and 2-Darrival angles of coherent signals[J]. Systems Engineering and Electronics, 2008, 30(6): 1050-1053. [本文引用:2]
[10]	杜刚, 张永顺, 王永良, 等. 基于四阶累积量的相干信号频率和二维到达角联合估计的新算法[J]. 电子与信息学报, 2009, 31(2): 327-330. Du Gang, Zhang Yong-shun, Wang Yong-liang, et al. A new method for joint estimating of frequency and 2-D arrival angles of coherent signals based on fourth-order cumulant[J]. Journal of Electronics and Information Technology, 2009, 31(2): 327-330. [本文引用:1]
[11]	Gu J F, Zhu W P, Swamy M N S. Compressed sensing for DOA estimation with fewer receivers than sensors[C]//IEEE International Symposium on Circuits & Systems, Rio de Janeiro, Brazil, 2011: 1752-1755. [本文引用:1]
[12]	沈志博, 赵国庆, 董春曦, 等. 基于压缩感知的频率和DOA联合估计算法[J]. 航空学报, 2014, 35(5): 1357-1364. Shen Zhi-bo, Zhao Guo-qing, Dong Chun-xi, et al. United frequency and DOA estimation algorithm based on compressed sensing[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1357-1364. [本文引用:1]

2016

0.0

. 2016, 46(2):632-638 DOI:doi:10.13229/j.cnki.jdxbgxb201602044

DOA tracking algorithm of moving targets with variable forgetting factor

时变遗忘因子动态DOA跟踪算法

Shan Ze-biao , Shi Yao-wu , Liu Xiao-song

单泽彪, 石要武, 刘小松

摘　要：针对目标信号源波达方向（DOA）实时变化的情况,提出了一种时变遗忘因子的自适应样本协方差矩阵更新方法。时变遗忘因子根据DOA变化的快慢自适应调节自身的大小,从而合理地调整历史数据及当前采样数据在协方差矩阵更新过程中所占的权重。在更新协方差矩阵后,对其直接应用最大似然估计方法,并将序列二次规划（SQP）应用于似然函数的优化求解上,最终实现了DOA的动态跟踪。仿真结果表明：该算法具有解相干的能力和良好的跟踪精度,并且在小样本、低信噪比下仍能达到比较满意的跟踪效果。

... 尽管最大似然方法^[1,2]是一种最优估计方法,但其需要多维穷尽搜索,应用常规搜索方法计算量巨大 ...

2015

0.0

. 2015, 23(7):2079-2085 DOI:doi:10.3788/OPE.20152307.2079

Joint estimation of DOA and Doppler frequency by SQP

应用序列二次规划的波达方向与多普勒频率联合估计

Shan Ze-biao , Shi Yao-wu , Shan Ze-tao

单泽彪, 石要武, 单泽涛

To estimate the Direction of Arrival (DOA)and Doppler frequency in array signal processing accurately and quickly,a joint spectrum estimation method based on maximum likelihood algorithm and Sequence Quadratic Program(SQP)was presented.With this method,a space-time signal model was used to construct a generalized array manifold matrix containing the information of DOAs and Doppler frequency based on the Hankel matrix,the joint spectrum was fitted using maximum likelihood algorithm,so that the joint parameter estimation was converted to multidimensional nonlinear function optimization.Then,the SQP algorithm was used to solve and optimize the maximum likelihood function and to obtain the estimation of DOAs and Doppler frequency.Finally,the simulation results were compared with the SQP method,differential evolution method,genetic method and quantum particle swarm optimization method. Experimental results indicate that the Root Mean Square Error(RMSE)of DOAs and Doppler frequency estimation are 0.2636掳and 0.0076 rad respectively under the condition of estimating two signal sources with 0 dB for SNR.It satisfies the requirements of design of joint parameter estimation method in the array signal processing.

... 尽管最大似然方法^[1,2]是一种最优估计方法,但其需要多维穷尽搜索,应用常规搜索方法计算量巨大 ...

1998

0.0

... Lemma等^[3]基于一维ESPRIT算法提出了一种联合角度与频率估计(JAFE)方法,该方法在有效降低计算量的同时仍具有较高的估计精度,但是其估计参数无法自动配对 ...

2006

0.0

... Lin等^[4]在无线通信领域中基于MUSIC算法提出了一种用于DOA与频率联合估计的FSF-MUSIC算法,该算法在具体运算过程中需要通过两次一维频率估计和一次一维角度估计来实现联合估计 ...

2014

0.0

. 2014, 22(9):2565-2571

Joint estimation of DOAs and Doppler frequency using isolation niche shuffled frog leaping algorithm

利用隔离小生境混合蛙跳方法联合估计波达方向和多普勒频率

Zhang Zhi-cheng , Wen Yan , Shi Yao-wu.

张志成, 温炎, 石要武

... 张志成等^[5]通过状态空间模型建立了包含DOA和多普勒频率两者信息的广义可观测矩阵,结合二维MUSIC算法及隔离小生境混合蛙跳方法实现了DOA与多普勒频率的联合估计 ...

... K)个全向天线构成的阵元间隔均为d的均匀线阵上,考虑信源运动导致多普勒频率存在的情况下,各信号的多普勒频率分别为f_k(k=1,2,…,K),则每个阵元接收到的信号可表示为^[5]: ...

... _M中的导向矢量同样正交于噪声子空间,所以DOA与多普勒频率联合估计的二维MUSIC空间谱函数可表示为^[5]: ...

2014

0.0

. 2014, 36(1):147-151

Multichannel joint frequency and DOA estimation based on expanded dimension

基于扩维的多通道联合频率和到达角估计

Zhao Man , Chen Hui.

赵曼, 陈辉

... 赵曼等^[6]针对宽频段信号角度与频率联合估计的欠采样问题,给出了一种基于扩维的联合估计算法 ...

2003

0.0

... 针对多径传播环境中相干信号的DOA与多普勒频率联合估计问题,文献[7]利用空间平滑预处理技术,通过构造时-空平滑数据矩阵实现了相干信号DOA与频率的联合估计,但是文献[7]仅利用了前向空间平滑技术,而忽略了与后向空间平滑技术的综合运用,以至于在阵元数较少的情况下估计精度相对较差 ...

... 为了提高阵元的利用率,文献[8]在文献[7]的基础上,结合前、后向空间平滑技术给出了一种相干信号联合波达角及频率估计的预处理方法,较大程度地提高了参数的估计性能 ...

2003

0.0

2008

0.0

. 2008, 30(6):1050-1053 DOI:doi:10.3321/j.issn:1001-506X.2008.06.012

Estimation of both the frequency and 2-Darrival angles of coherent signals

空间相干信号的频率和二维到达角估计算法

Du Gang , Wang Yong-liang , Zhang Yong-shun

杜刚, 王永良, 张永顺

针对宽频段窄带信号的参数估计,提出了一种空间相干信号频率和二维到达角联合估计的算法--TSS-DOA算法.TSS-DOA算法利用双平行线阵的时空数据以及平滑技术构造了一个时空平滑矩阵,通过对其进行特征分解,并利用分解得到的特征值和特征矢量估计出空间相干信号的三维参数.该算法能精确地估计信号的三维参数,无需多维谱峰搜索,具有计算量小,三维参数自动配对的优点,并有效地解决了信源参数兼并问题.计算机仿真结果验证了算法的有效性.

... 杜刚等^[9,10]同样利用空间平滑技术并结合双平行线阵的时空数据结构,实现了空间相干信号的频率及二维波达方向的估计 ...

... 图5(a)(b)分别给出了上述3种算法在不同信噪比条件下的DOA与多普勒频率联合估计的均方根误差及相应的克拉美罗界(CRB)^[9] ...

2009

0.0

. 2009, 31(2):327-330

A new method for joint estimating of frequency and 2-D arrival angles of coherent signals based on fourth-order cumulant

基于四阶累积量的相干信号频率和二维到达角联合估计的新算法

Du Gang , Zhang Yong-shun , Wang Yong-liang

杜刚, 张永顺, 王永良

该文提出了一种基于四阶累积量的相干信号频率和二维到达角联合估计的新算法-CTSS算法.CTSS算法利用双平行线阵的时空数据以及平滑技术构造了一个时空平滑矩阵,通过对其进行特征分解,并利用分解得到的特征值和特征矢量估计出空间相干信号的三维参数.在色噪声环境下,该算法能够精确地估计空间相干信号的三维参数,无需多维谱峰搜索,能实现信号三维参数的自动配对,并有效地解决了信源参数兼并问题.计算机仿真结果验证了算法的有效性.

... 杜刚等^[9,10]同样利用空间平滑技术并结合双平行线阵的时空数据结构,实现了空间相干信号的频率及二维波达方向的估计 ...

2011

0.0

... 文献[11,12]利用空间信号本身存在的稀疏特性,结合压缩感知理论研究了DOA与频率的联合估计问题 ...

2014

0.0

. 2014, 35(5):1357-1364

United frequency and DOA estimation algorithm based on compressed sensing

基于压缩感知的频率和DOA联合估计算法

Shen Zhi-bo , Zhao Guo-qing , Dong Chun-xi

沈志博, 赵国庆, 董春曦

... 文献[11,12]利用空间信号本身存在的稀疏特性,结合压缩感知理论研究了DOA与频率的联合估计问题 ...