希尔伯特-黄变换^[1](Hilbert-Huang trans-form, HHT)是近年来发展十分迅速的一种处理非线性、非平稳信号的有效方法。该方法能够根据信号的自身特性, 采用经验模态分解(Empirical mode decomposition, EMD)将非平稳信号分解成一系列具有不同特征尺度的固有模态函数(Intrinsic mode functions, IMF), 有效地提取出信号的本质特征。并通过Hilbert变换得到表征信号时间-频率-能量三者关系的Hilbert谱, 该谱图能够突显信号的局部特征, 具有良好的时频分辨能力^[2]。因此, 被广泛应用于机械^[3]、电力^[4]、金融^[5]、医学^[6]等众多领域。

EMD是HHT方法的核心, 其分解结果的优劣将直接影响HHT分析的准确性。由于EMD方法忽略了信号所拟合的包络线在端点处的约束^[7], 导致每次样条插值产生拟合误差, 随着误差的不断累积, 分解出的各阶IMF分量在端点处产生发散现象; 并且在分解多频率分量的非平稳信号时, 会产生单一IMF分量中包含截然不同的频率成分或同一频率成分被分解到不同的IMF分量中的问题^[8]。当发生上述问题时, EMD所分解出的IMF分量不具有真实的物理意义, 难以表达信号特征。为此, 国内外研究学者提出了很多方法, 如:支持向量回归机^[9]、波形匹配延拓^[10]、斜率再优化延拓^[11]、优化Hermite插值法^[12]等用于抑制端点效应问题; 同时, 采用总体平均经验模态分解^[13](Ensemble empirical mode decom-position, EEMD)解决模态混叠问题, 并都取得了一定的效果。

本文针对EMD分解过程中的模态混叠等问题, 提出了一种基于最优特性的自适应白噪声平均总体经验模态分解(Optimal feature complete ensemble empirical mode decomposition with adaptive noise, OFCEEMDAN)方法。该方法采用边界局部均值延拓抑制端点效应问题, 同时, 自适应地向信号中添加白噪声, 通过计算唯一的残余信号来获得信号的各阶IMF分量, 达到解决模态混叠的问题。通过仿真研究和对实际信号的分析, 验证了该方法不仅能够有效抑制端点效应问题, 同时可有效避免模态混叠问题的发生。

EEMD(Ensemble EMD)是目前最为常用的改善EMD所存在模态混叠问题的方法, 其主要思想是向原信号中添加不同幅值的白噪声来获得新的极值点, 并将多次EMD分解所得IMF的均值作为最终的真实IMF分量。在多次总体平均获取IMF分量的同时, 不同幅值白噪声对于原信号的影响也得到了抵消。然而, 经EEMD分解后所得的IMF分量中仍有一定幅值的噪声残留^[14], 虽然通过增加总体平均次数可以减少残留噪声, 但增加了算法的计算量, 这将直接导致虚假模态分量的产生。

为解决EEMD分解过程中所存在的问题, 同时抑制EMD分解过程中产生的端点效应问题, 本文提出了OFCEEMDAN方法。该方法以基于边界局部均值延拓的EMD为核心, 首先, 利用信号两侧端点和其临近的两个极值点的特征, 对包络线在信号两端点处的值进行均值估计, 并将估计值添加到极值序列中。然后, 为防止信号端点成为最值点, 出现较大拟合误差的情况, 对估计值和端点值进行比较, 选取最优的延拓极值点, 从而达到抑制端点效应的目的。

定义运算符E_k(· )为通过边界局部均值延拓的EMD方法所得到的第k阶IMF分量; < · > 为求解信号的平均值; wⁱ为包含不同幅值的高斯白噪声。

采用OFCEEMDAN方法对于信号xⁱ=x+β ₀wⁱ进行分解的具体分解步骤如下所示。

(1)进行I次试验, 采用基于边界局部均值延拓的EMD对xⁱ进行分解, 将得到的第1阶IMF分量取均值, 即为OFCEEMDAN的第1阶IMF分量:

d~1=d-1=< E1(xi)> (1)

(2)信号的第1个残余分量为:

r1=x-d~12

(3)同样进行I次试验, 并对信号r₁+β ₁E₁(wⁱ)进行基于边界局部均值延拓的EMD分解, 当得到第1阶IMF分量时分解停止, 此时, 第2阶IMF分量为:

d~2=< E1(r1+β1E1(wi)> (3)

(4)对余下的每个阶段, k=2, 3, …, K, 计算第k个残余分量:

rk=rk-1-d~k4

(5)采用基于边界局部均值延拓的EMD分解r_k+β _kE_k(wⁱ)(i=1, 2, …, I)至第1阶模态分量, 并定义第k+1阶OFCEEMDAN的模态分量为:

d~k=< E1(rk+βkEk(wi)> (5)

(6)执行步骤(4), 并将k加1。当残余信号的极值点个数不超过2时分解结束。

分解结束时, 设所有模态分量的数量为K, 则最终的残差信号为:

rK=x-∑k=1Kd~K6

因此, 原信号经OFCEEMDAN分解后可表示为:

x=∑k=1Kd~K+rK7

在每一个模态分解阶段, 根据系数β _k=ε ₀std(r_k)(k≥ 1)可实现信噪比的自主选择, 从而达到自适应添加噪声的目的。其中, β ₀=ε ₀std(x)/std(E₁(wⁱ)), ε ₀为所添加噪声的标准差。

由OFCEEMDAN分解过程可知, 其不仅具备了EEMD的抗模态混叠性能, 同时, 该方法分解过程相对于EEMD更加完整, 而分解的每个阶段自适应地添加有限次白噪声, 能够保证在平均次数相对少的情况下, 对信号进行精确重构, 并避免了EEMD为克服分解不完整和提高重构精度而导致的分解效率低的问题。此外, 该方法以基于边界局部均值延拓优化的EMD方法为核心算法, 有效避免了EMD分解过程中所产生的端点效应, 使分解结果最优。

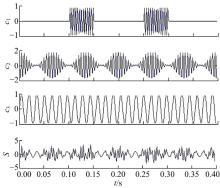
为验证本文方法的有效性, 仿真一组由小幅冲击成分c₁、调制分量c₂和谐波c₃组成的信号S, 如图1所示。对于旋转机械而言, 其正常工作时的运动呈现周期性的特点, 可用谐波分量表示。当旋转机械中出现损伤故障时, 通常表现出高频冲击和调制响应的特性^[15], 因此, 仿真信号S具有一定的普遍性。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 仿真信号Fig.1 Simulated signal

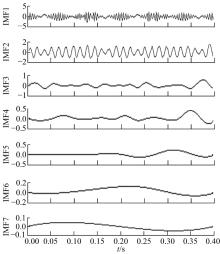
利用本文所提出的OFCEEMDAN方法对仿真信号S进行分解, 其中, 所添加白噪声的标准差ε ₀=0.2, 总体试验次数I=500, 分解得到的各IMF分量如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 仿真信号的OFCEEMDAN分解结果Fig.2 OFCEEMDAN decomposition results of simulated signal

由图2可以看出, 分解得到的前3阶IMF分量分别对应着仿真信号中的冲击成分c₁, 调制分量c₂和谐波信号c₃, 各IMF分量之间不存在模态混叠现象, 同时, 分解得到的虚假分量较少, 与仿真信号吻合。

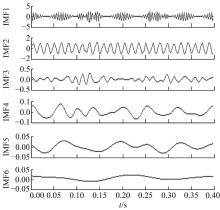
为进行对比, 分别采用EMD和EEMD方法对上述仿真信号进行分解, 结果如图3和图4所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 仿真信号EMD分解结果Fig.3 EMD decomposition results of the simulated signal

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 仿真信号EEMD分解结果Fig.4 EEMD decomposition results of simulated signal

从图3和图4中不难看出:EMD和EEMD方法的分解结果均出现了不同程度的模态混叠, 其中两种分解方法得到的IMF1分量中既包括冲击成分, 也含有调制成分; 相较于EEMD方法, EMD方法分解得到的IMF2与仿真信号的谐波成分相比, 失真更加严重; 同时, 两种分解方法的结果中都出现了较多的虚假和干扰分量。

为更加准确地分析不同分解方法的优劣, 定义如下指标作为评价因子对上述方法进行定量分析。

(1)正交指数Ort

Ort=∑t=0N∑i=1n+1∑j=1n+1ci(t)cj(t)/x2(t), i≠j8

式中:c_i(t)和c_j(t)分别为信号x(t)的第i阶和第j阶IMF分量; n为信号x(t)中IMF分量的总阶数。

正交指数Ort是一个总体的判定标准:Ort的值越大表示各IMF分量间的相关性越大, 则它们间的正交性越低。在理想情况下, 各阶IMF分量间应完全正交, 但由于端点效应问题的存在, 经EMD分解后的各阶IMF分量无法满足完全正交, Ort的值越低表明各IMF分量间的正交性越好, 即分解过程中所受端点效应的影响越小。因此, Ort可作为评价抑制EMD端点效应的有效指标。

(2)迭代次数Ins

采用不同的极值延拓和信号分解方式都会导致在IMF分量筛分的过程中的迭代次数不同。每一阶IMF分量所需的迭代次数越少, 说明所选用的方法运算效率越高。

(3)重构误差Rce

Rce主要用于保证信号的完备性, Rce越大表明分解过程中信号的信息损失越多, 后续分析中很可能由于信号中关键信息的损失造成分析结果出现严重偏差。在此, Rce取重构误差信号中的纵坐标绝对值的最大值作为评价因子。表1为不同方法对仿真信号分解后的评价因子对比。

表1

Table 1

表1(Table 1)

表1 不同分解方法的仿真信号评价因子 Table 1 Evaluation factors of simulated signal 方 法 评价因子 Ort Ins Rce EMD 0.0402 2195 4.4409´ 10-16 EEMD 0.0258 27248 0.0279 OFCEEMDAN 0.0093 14225 8.8818´ 10-16

表1 不同分解方法的仿真信号评价因子 Table 1 Evaluation factors of simulated signal

由表1可知, 虽然EMD方法在每次分解IMF分量过程中的迭代次数和重构误差都比较小, 但其无法解决自身的模态混叠问题, 而正交指数过大, 也表明端点效应并未得到有效抑制, 这些问题限制了该方法的应用; EEMD方法具有一定的抗模态混叠特性, 但该方法主要应用于解决模态混叠问题, 因此, 端点效应问题并未得到抑制, 同时需要对含噪信号通过有限次集成平均, 为此, 其IMF分量和重构信号中仍有噪声残留, 这致使其重构误差明显高于其他两种方法, 在总体平均次数并不大的情况下, EEMD方法的迭代总次数达到27 248次, 分解效率较低。

与上述两种方法相比, OFCEEMDAN能够有效抑制端点效应的产生, 由于是自适应地添加噪声, 能够在较少平均次数下, 消除IMF分量中的噪声成分, 因此, 其重构误差相几乎为0, 分解所用总体迭代次数为14 225次, 相比EEMD方法, 迭代总次数减少了47.79%, 有效提高了分解效率。

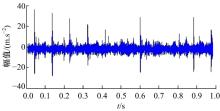
选用图5所示的齿轮箱故障信号进行分析, 其中故障原因为从动齿轮点蚀故障。所用齿轮箱为一级减速器, 齿轮箱由输入轴通过联轴器与驱动电机相连。驱动齿轮和从动齿轮均为标准直齿轮, 模数为2 mm, 齿数分别为55和75。加速度传感器安装在靠近从动齿轮负载一侧的轴承座上, 采样频率为5120 Hz, 采样时间为1 s。输入轴转速为880 r/min, 驱动齿轮的转频f₁=14.67 Hz, 由传动比可知, 从动齿轮转频f₂=10.48 Hz。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 齿轮箱故障信号Fig.5 Gear box fault signal

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同方法的齿轮箱故障信号分解结果Fig.6 Decomposition results of gear box fault signal

采用不同分解方法对齿轮箱故障信号进行分解, 可以将此复杂信号分解成包含不同频率成分的模态函数信号, 从而获得信号的高频故障成分, 实现对其故障信息的获取。采用EMD、EEMD和OFCEEMDAN方法对故障信号进行分解, 分别得到10阶、12阶和8阶IMF分量, EEMD和OFCEEMDAN方法所添加的噪声标准差ε ₀=0.01, 总体试验次数I=100。图6为不同方法的分解结果, 其中EMD和EEMD取前9阶IMF分量进行对比分析。

由图6可知, 采用EMD和EEMD方法对端点效应的抑制效果并不理想, 各低频分量产生明显的失真, 端点处幅值偏差过大; 同时, EMD的抗模态混叠性能不佳, 分解得到的各IMF分量间存在严重的模态混叠问题, 而EEMD方法所分解出的IMF5、IMF6以及IMF7与IMF8之间都存在明显的模态混叠, 这势必将影响齿轮箱信号故障特征提取的有效性。

图7为不同分解方法所获得高频分量IMF1的包络谱。由图7(c)可以清楚地看出, 在IMF1的包络谱中10.46 Hz和21.37 Hz处有明显的谱线出现。而10.46 Hz和21.37 Hz分别为从动齿轮转频的1倍频和2倍频, 同时高频成分被削弱, 根据齿轮振动机理, 可判定与输出轴相连的从动齿轮存在故障, 而当齿轮发生点蚀故障时, 其低倍转频成分被加强并且啮合频率和高频成分被削弱^[16], 与图7(c)所示结果相一致。图7(a)和7(b)中, 由于端点效应和模态混叠问题的影响, 分解得到的高频IMF1分量混叠了其他频率成分, 导致IMF1包络谱中存在很多干扰成分, 10.76 Hz和21.64 Hz的谱线特征不明显, 降低了故障特征提取的准确性和故障诊断的可靠性。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 不同方法分解出的高频分量IMF1包络谱Fig.7 Envelope spectrum of IMF1 with different method

OFCEEMDAN方法由于以平均极值延拓的EMD为核心, 同时, 在分解的每个阶段自适应地添加有限次白噪声, 因此, 该方法所分解出的各阶IMF分量在抑制端点效应和模态混叠问题上都明显优于EMD和EEMD方法。表2为不同方法对齿轮箱故障信号分解后的评价因子对比, 由各评价因子可进一步表明该方法的有效性。

表2

Table 2

表2(Table 2)

表2 不同分解方法的齿轮箱故障信号评价因子 Table 2 Evaluation factors of gear box fault signal 方 法 评价因子 Ort Ins Rce EMD 0.3063 105 0.2 EEMD 0.0876 20183 0.01219 OFCEEMDAN 0.0293 11615 1.78´ 10-15

表2 不同分解方法的齿轮箱故障信号评价因子 Table 2 Evaluation factors of gear box fault signal

(1)以边界局部均值延拓为核心的OFCEEMDAN方法, 具有较好的抗模态混叠性能, 由于在分解的每个阶段自适应地添加有限次白噪声, 能够保证在平均次数相对少的情况下, 对信号进行精确重构, 并避免了EEMD方法所存在的分解效率低和IMF分量中噪声残留的问题; 同时有效解决了EMD分解过程中的端点效应问题。

(2)通过仿真信号和齿轮箱故障信号的分析, 证明了该方法能够有效提取出复杂信号中所包含的各频率分量, 具有一定的工程实际应用价值。