基于相似匹配维纳滤波的地震资料噪声压制

引用本文

李娟, 孟可心, 李月, 刘慧力. 基于相似匹配维纳滤波的地震资料噪声压制[J].吉林大学学报（工学版）, 2017,47(6): 1964-1968
LI Juan, MENG Ke-xin, LI Yue, LIU Hui-li. Seismic signal noise suppression based on similarity matched Wiener filtering[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1964-1968 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706039
Permissions

基于相似匹配维纳滤波的地震资料噪声压制

李娟¹, 孟可心¹, 李月¹, 刘慧力²

1.吉林大学通信工程学院,长春 130012

2.吉林大学生物与农业工程学院,长春 130022

通讯作者：刘慧力(1970-),男,工程师.研究方向:测控技术及工业电气自动化.E-mail:liuhuili@163.com

作者简介:李娟(1970-),女,副教授,博士.研究方向:地震信号处理.E-mail:ljuan@jlu.edu.cn

基金:国家自然科学基金项目(41574096)

摘要

针对强噪声背景下地震资料噪声压制困难的问题,提出一种基于地震信号相似性的维纳滤波传递函数优化算法。该算法将待处理资料分块,并依据地震同相轴的时空相似性构建三维相似组。经过低秩近似,信号与噪声差异明显,能够计算得出更为精确的维纳滤波传递函数。经过仿真信号与真实地震资料的对比验证,采用本文优化算法得到的传递函数进行维纳滤波,既能实现随机噪声的有效压制,又能极大地保护信号的有效成分。

关键词: 信息处理技术; 维纳滤波; 块匹配; 奇异值分解

中图分类号:TN911.7 文献标志码:A 文章编号:1671-5497(2017)06-1964-05

Seismic signal noise suppression based on similarity matched Wiener filtering

LI Juan¹, MENG Ke-xin¹, LI Yue¹, LIU Hui-li²

1.College of Communication and Engineering, Jilin University, Changchun 130012, China

2.College of Biological and Agricultural Engineering, Jilin University, Changchun 130022, China

Abstract

Seismic exploration is the main method in oil and gas exploration. It becomes more and more difficult to identify the collected seismic signals, because of a sharp drop in resolution and the Signal to Noise Ratio (SNR). Conventional seismic record processing methods have shown no adaptability to very low SNR. In order to realize the requirement of high SNR, high resolution and high fidelity of seismic data processing in strong noise, this paper proposes a novel method of seismic data noise suppression based on similarity matched Wiener filtering. In this method, based on the local and non-local similarity of seismic events, the whole record is divided into overlapping sub-blocks and the blocks containing similar signals are found out by some distance measures. Then, the low rank matrix is constructed by Singular Value Decomposition (SVD) and the smaller singular values are removed representing noise. The noise in the constructed signal is effectively suppressed. Using this estimation, the Wiener filter is able to obtain a more accurate transfer function. At the same time, the effect of prior information on noise suppression is eliminated. Experiment results illustrate that the proposed method improves the SNR and effectively retains the signal amplitude.

Keyword: information processing technology; Wiener filtering; block matching; singular value decomposition

Show Figures

0 引言

近年来, 随着易开采资源的不断减少以及地表条件的复杂化, 检波器接收到的地震信号的信噪比及分辨率越来越低^[1]。为了保持油气藏定位的准确性, 地层分析之前的信号处理越发重要。原有的地震资料处理方法已经显示出对低信噪比信号的不适应性。

F-K滤波是建立在二维傅里叶变换基础上的处理方法^[2]。它根据有效信号与噪声的视速度差异完成噪声压制, 主要应用于去除频率较低、能量较强、呈扫帚状频散的面波噪声。τ -p变换又称倾斜叠加, 它的实质是离散化的Radon变换, 主要针对地震资料中的倾斜干扰^[3]。

基于多尺度分析的小波变换方法采用传统小波变换, 将地震资料分解到不同的尺度并设置相应的阈值, 以求得到压制噪声的效果^[4]。但小波变换在处理二维信号方面存在方向局限性, 并不能很好地描述有效信号的方向信息, 严重影响去噪结果。近年来多尺度几何分析法在图像融合、特征提取等领域均有广泛的应用。例如Ridgelet变换^[5]、Curvelet变换^[6]、Contourlet变换^[7]、Shearlet变换^[8]等。多尺度几何分析法具有多分辨率、多方向性、多尺度化的特点, 通过少数非零变换系数就能够重构有效信号。但是, 上述稀疏变换为非下采样变换, 在处理实际地震信号时, 由于数据采样密度较大, 往往造成算法的时间复杂度较高, 因而在实时性方面性能较差。

为了满足强噪声背景下的地震资料处理需求, 本文提出一种基于相似匹配的维纳滤波优化方法。一方面, 该方法从地震信号相似特性出发, 重构低秩矩阵, 优化维纳传递函数。另一方面, 该方法消除了传统维纳滤波算法中对信号和噪声先验统计知识的需求。

1 基本理论

维纳滤波是利用平稳随机过程的相关特性或者频谱特性对含噪信号进行滤波的方法, 它是最小均方误差准则下的一种线性估计。即对于信号 $\begin{matrix} X \end{matrix}$ 及其估计 $\begin{matrix} \hat{X}, \end{matrix}$ 均方误差 $\begin{matrix} E [e^{2}] \end{matrix}$ 满足:

$\begin{matrix} E {[e^{2}]}_{\min} = E {[{(\hat{X} - X)}^{2}]}_{\min} (1) \end{matrix}$

通过求解使均方差最小的维纳-霍夫方程, 并将得到的最优系统单位脉冲响应 $\begin{matrix} h_{opt} (t) \end{matrix}$ 变换到频域就可以得到维纳滤波的频域表示。由于信号与噪声互不相关, 且信号的自相关函数与功率谱密度互为傅里叶变换对, 因此频域维纳滤波的传递函数 $\begin{matrix} H_{opt} (f) \end{matrix}$ 可以表示为:

$\begin{matrix} H_{opt} (f) = \frac{S_{ss} (f)}{S_{ss} (f) + S_{nn} (f)} (2) \end{matrix}$

式中: $\begin{matrix} S_{ss} (f) 、 S_{nn} (f) \end{matrix}$ 分别为地震信号的能量谱密度函数和噪声的功率谱密度函数。

传统的维纳滤波需要信号和噪声的统计特性作为先验知识。而在工程实际中, 由于先验知识未知, 维纳滤波并不能获得最优的传递函数解。另一方面, 在强噪声低信噪比条件下, 传统维纳滤波会导致有效信号幅度的衰减严重^[9]。

2 相似匹配维纳滤波

炮点放炮产生的地震同相轴具有时空相似性, 而检波器附近的背景噪声显然是随机的。信号的相似特性使得纯净信号的矩阵是低秩的。因此, 本文提出了奇异值低秩近似的维纳滤波传递函数优化方法。

2.1 维纳传递函数优化

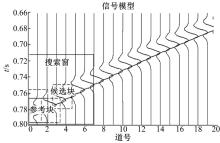
本文优化维纳滤波系统函数的主要方法就是获取清晰背景下信号的能量谱密度函数 $\begin{matrix} S_{ss} (f) 。 \end{matrix}$ 而清晰的背景环境是相似匹配后通过奇异值分解实现的。

2.1.1 相似性分组

为方便衡量地震同相轴间的相似水平, 将原始地震资料过完备地分解成 $\begin{matrix} N_{1} \times N_{1} \end{matrix}$ 的子块 $\begin{matrix} Y_{x}, \end{matrix}$ 如图1所示。在大小为 $\begin{matrix} h \times h \end{matrix}$ 的邻域搜索窗内, 搜索与当前选定参考块 $\begin{matrix} Y_{R} \end{matrix}$ 相似的候选块。相似的判别准则为表征两块幅值差异的欧氏距离 $\begin{matrix} d (Y_{R}, Y_{x}), \end{matrix}$ 即:

$\begin{matrix} d (Y_{R}, Y_{x}) = \frac{‖ r' (T (Y_{R})) - r' (T (Y_{x})) ‖_{2}^{2}}{{N_{1}}^{2}} (3) \end{matrix}$

式中: $\begin{matrix} T (\cdot) \end{matrix}$ 为傅里叶变换, 求出块的二维频谱。

	Figure Option View Download New Window
	图1 块匹配示意图Fig.1 Schematic of block-matching

为了避免噪声方差过大引起分组错误, 将阈值 $\begin{matrix} r' \end{matrix}$ 处理后的子块频谱 $\begin{matrix} r' (T (Y_{x})) \end{matrix}$ 作为计算块间距离的元素。当两个子块的距离d(Y_R, Y_x)小于阈值τ时, 判定两块相似, 然后将所有与同一参考块相似的二维时域子块 $\begin{matrix} Y_{x}, \end{matrix}$ 连同参考块一起构建成一个三维数组, 即相似组 $\begin{matrix} Z_{R} 。 \end{matrix}$

2.1.2 奇异值分解去噪

首先对 $\begin{matrix} Z_{R} \end{matrix}$ 进行二维离散余弦变换。在频率域, 不同道的地震信号具有相同的有效频带, 即各地震道有效频带的频谱存在较好的相干性, 满足低秩条件, 而噪声是随机的, 频带较宽^[10]。在噪声的影响下, 相似组 $\begin{matrix} Z_{R} \end{matrix}$ 的频谱是满秩的。为了获取相似组的估计采用基于奇异值分解重构的低秩逼近方法。

对于一个相似组中的任意一个二维子块的频谱 $\begin{matrix} F (Y_{x}), \end{matrix}$ 它的特征矩阵 $\begin{matrix} U_{2 D} \end{matrix}$ 和 $\begin{matrix} V_{2 D} \end{matrix}$ 分别根据它的行-行协方差矩阵和列-列协方差矩阵求得, 将 $\begin{matrix} F (Y_{x})_{i}, i \in [0, N - 1] \end{matrix}$ 投影到 $\begin{matrix} U_{2 D} \end{matrix}$ 和 $\begin{matrix} V_{2 D} \end{matrix}$ 上, 得到的投影系数 $\begin{matrix} Λ_{i}, \end{matrix}$ 满足:

$\begin{matrix} F (Y_{x})_{i} = U_{2 D} Λ_{i} {V^{T}}_{2 D} (4) \end{matrix}$

式中: $\begin{matrix} Λ_{i} \end{matrix}$ 为奇异值按非增顺序组成的对角阵。

由于奇异值分解的能量汇聚特性, 具有较强相似性的信号能量集中在较大的奇异值上, 而随机噪声的能量零散分布在较小的奇异值中。另外, 二维奇异值分解关注每个子块中列之间的相似性, 即地震道间的局部相似性。因此, 选用前 $\begin{matrix} k \end{matrix}$ 个最大的奇异值对应的本征矩阵重建地震记录, 可以有效地消除地震资料的局部随机噪声。

考虑到组中子块间的非局部相似性, 可以借助这一特性进一步去除块间冗余。假设相似组Z_R中共有M个相似块, 将每个子块向量化后依次排列, 组成 $\begin{matrix} N_{1} \times N_{1} 行, M \end{matrix}$ 列的新矩阵 $\begin{matrix} F (Y) 。 \end{matrix}$ 此矩阵必然存在两个正交矩阵 $\begin{matrix} U_{1 D} \end{matrix}$ 以及 $\begin{matrix} V_{1 D} \end{matrix}$ 满足:

$\begin{matrix} F (Y) = U_{1 D} Λ_{1 D} {V^{T}}_{1 D} (5) \end{matrix}$

式中: $\begin{matrix} Λ_{1 D} \end{matrix}$ 为奇异值按非增顺序组成的对角阵, 将较小的奇异值去除可以实现块间冗余的消减。

2.1.3 加权聚合

将处理后的奇异值矩阵重构, 可以得到噪声压制后的频域数据块, 将其进行二维离散余弦反变换, 得到该相似组所有子块在对应位置的时域的基础估计。但由于分块是过完备的, 因此分组中的块可能存在重叠部分, 同一子块也有可能被不同相似组同时使用。因此, 为得到清晰背景下的基础估计 $\begin{matrix} {\hat{Y}}^{basic}, \end{matrix}$ 本文还需要对当前过完备的块估计进行加权聚合:

$\begin{matrix} {\hat{Y}}^{basic} = \frac{\sum_{Y_{R}} \sum_{Z_{R}} ω_{R}^{h t} \times {\hat{Y}}_{R}}{\sum_{Y_{R}} \sum_{Z_{R}} ω_{R}^{h t}} (6) \end{matrix}$

对应权重 $\begin{matrix} ω_{R}^{h t} \end{matrix}$ 计算方法为:

$\begin{matrix} ω_{R}^{h t} = \frac{1}{σ^{2} \times N_{R}} (7) \end{matrix}$

式中: $\begin{matrix} σ^{2} \end{matrix}$ 为噪声方差; $\begin{matrix} N_{R} \end{matrix}$ 为未置0的元素个数。

2.2 三维维纳滤波

基础估计 $\begin{matrix} {\hat{Y}}^{basic} \end{matrix}$ 虽然有效地压制了地震资料中包含的背景噪声。但是, 由于奇异值保留个数较难确定, 不准确的奇异值保留会造成降噪后信号中出现大量“ 毛刺” , 波动明显。因此, 基础估计 $\begin{matrix} {\hat{Y}}^{basic} \end{matrix}$ 仅作为优化维纳滤波传递函数的先验信号使用。

对基础估计再次分块, 并在时域重新计算块间欧氏距离, 方法与2.1.1小节类似。然后将分组方式传递给对应的原始带噪块组成新的相似组 $\begin{matrix} Z_{R}^{wie}, \end{matrix}$ 并对原始带噪信号进行三维维纳滤波:

$\begin{matrix} {\hat{Y}}^{wie} = T_{3 D}^{- 1} (W_{R} T_{3 D} (Z_{R}^{wie})) (8) \end{matrix}$

式中: $\begin{matrix} T_{3 D} (\cdot) \end{matrix}$ 为三维离散余弦变换; $\begin{matrix} W_{R} \end{matrix}$ 为维纳收缩系数, 是频域维纳滤波传递函数的表示方式, 其计算方法如下:

$\begin{matrix} W_{R} = \frac{{|T_{3 D} ({\hat{Y}}_{Z_{R}}^{basic})|}^{2}}{{|T_{3 D} ({\hat{Y}}_{Z_{R}}^{basic})|}^{2} + σ^{2}} (9) \end{matrix}$

式中: $\begin{matrix} σ^{2} \end{matrix}$ 代表噪声的功率, 在数值上等于噪声方差, 而信号频域的幅度平方代表信号的能量值。

由于基础估计已经基本实现噪声压制和信号恢复, 因此计算得到的维纳收缩系数在噪声部分接近于0, 而在信号部分接近于1, 因此能实现有效信号的保留和噪声的压制。对过完备块再次加权聚合得到最终估计 $\begin{matrix} \hat{Y} 。 \end{matrix}$ 新的聚合权重 $\begin{matrix} ω_{R}^{wie} \end{matrix}$ 计算方法如下:

$\begin{matrix} ω_{R}^{wie} = σ^{- 2} \times {||\frac{{|T_{3 D} ({\hat{Y}}_{Z_{R}}^{basic})|}^{2}}{{|T_{3 D} ({\hat{Y}}_{Z_{R}}^{basic})|}^{2} + σ^{2}}||}_{2}^{- 2} (10) \end{matrix}$

在维纳滤波过程中重新对原始带噪信号做滤波处理能有效地保留信号的幅度, 同时避免尖峰毛刺等奇点。

3 仿真及实际信号试验

3.1 仿真信号试验

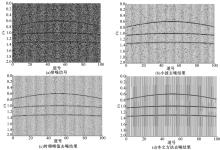
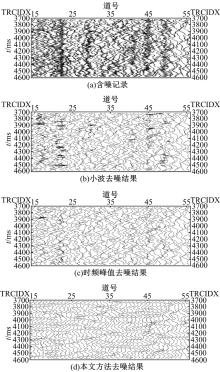
为了验证基于相似匹配维纳滤波噪声压制方法的可行性及有效性, 本文模拟了100道地震资料。资料中包含3条同相轴, 主频分别为25、35和45 Hz。地震资料采样频率为1000 Hz, 炮检距为30 m并加入-5 dB的高斯白噪声, 仿真结果如图2所示。可以看出本文方法去噪效果更好, 得到的同相轴更为清晰, 背景噪声更少。从信噪比的角度, 经小波阈值处理后SNR提高到4.01 dB, 经时频峰值滤波处理后SNR提高到4.16 dB, 经本文方法处理后SNR提高到16.86 dB。

为了清晰展示两种方法的噪声压制效果, 图3给出了单道信号的时域图和频谱图。可以清晰地看出, 本文方法在压制噪声的同时更好地保留了有效信息。尤其在大于200 Hz的高频部分, 噪声得到了更为有效的压制。

3.2 实际信号试验

将本文方法应用于中国某测区取得的实际地震资料中。该地震资料包含168个地震道, 每道包含6000个采样点。为清晰起见选择其中部分结果进行展示, 结果如图4所示。可以看出, 经本文方法处理后的地震资料同相轴更为清晰、连续。

	Figure Option View Download New Window
	图2 仿真试验对比图Fig.2 Comparison of simulation experiment

	Figure Option View Download New Window
	图3 单道信号的时域图和频谱图Fig.3 Time domain and amplitude spectrum of single channel

	Figure Option View Download New Window
	图4 实际地震信号对比图Fig.4 Comparison of real seismic record

4 结束语

本文基于地震同相轴固有的局部和非局部相似性, 提出了优化维纳滤波传递函数的地震噪声压制方法。利用相似性将信号子块组合成三维矩阵, 实现相似组低秩。用二维奇异值分解去除相似组块内冗余, 一维奇异值分解去除相似组块间冗余。将重构的得到的基础估计作为维纳传递函数的先验信息, 从而得到更为准确的收缩比例, 最后经优化的维纳滤波系数实现了对原始带噪信号的噪声压制。经过仿真信号以及实际地震记录验证, 本方法压制噪声效果明显, 且能更好地保留同相轴有效信息。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李道品. 低渗透砂岩油田开发[M]. 北京: 石油出版社, 1997. [本文引用:1]
[2]	张军华, 吕宁, 田连玉, 等. 地震资料去噪方法技术综合评述[J]. 地球物理学进展, 2006, 21(2): 546-553. Zhang Jun-hua, Lv Ning, Tian Lian-yu, et al. An overview of the methods and techniques for seismic data noise attenuation[J]. Progression Geophysics, 2006, 21(2): 546-553. [本文引用:1]
[3]	Famoush F A, Mike B, Jyoti B. Noise suppression in surface microseismic data[J]. The Leading Edge, 2012, 31(12): 1496-1501. [本文引用:1]
[4]	徐宏斌, 李庶林, 陈际经. 基于小波变换的大尺度岩体结构微震监测信号去噪方法研究[J]. 地震学报, 2012, 34(1): 85-96. Xu Hong-bin, Li Shu-lin, Chen Ji-jing. A study on method of signal denoising based on wavelet transform for micro-seismicity monitoring in large-scale rockmass structures[J]. Acta Seismologica Sinica, 2012, 34(1): 85-96. [本文引用:1]
[5]	王梅, 侯振杰, 吕国玲, 等. 基于Ridgelet变换的多尺度去噪算法研究[J]. 微型机与应用, 2012, 31(2): 25-27. Wang Mei, Hou Zhen-jie, Lv Guo-ling, et al. A multi-scale method for image denoising based on Ridgelet transform[J]. Microcomputer & Its Applications, 2012, 31(2): 25-27. [本文引用:1]
[6]	Srarck J L, Cand es E J, Donoho D L. The curvelet transform for image denoising[J]. IEEE Transactions on Image Processing, 2002, 11(6): 670-684. [本文引用:1]
[7]	谢成芳, 彭真明, 周晶晶, 等. 基于Contourlet 变换的地震多属性融合方法[J]. 石油地球物理勘探, 2014, 49(4): 739-744. Xie Cheng-fang, Peng Zhen-ming, Zhou Jing-jing, et al. Multi attribute fusion method for seismic signal based on contourlet transform[J]. Oil Geophysical Prospecting, 2014, 49(4): 739-744. [本文引用:1]
[8]	Hu H, Sun H, Deng C, et al. Image denoising algorithm based on shearlet transform[J]. Journal of Computer Application, 2010, 30(6): 1562-1564. [本文引用:1]
[9]	田雅男, 李月, 林红波, 等. 基于频域正则维纳滤波的地震随机噪声压制[J]. 吉林大学学报: 工学版, 2015, 45(6): 2043-2048. Tian Ya-nan, Li Yue, Lin Hong-bo, et al. Frequency-domain regularized wiener filtering for seismic rand om noise suppression[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(6): 2043-2048. [本文引用:1]
[10]	沈鸿雁, 李庆春. 频域奇异值分解(SVD)地震波场去噪[J]. 石油地球物理勘探, 2010, 45(2): 185-189. Shen Hong-yan, Li Qing-chun. Seismic wave field separation and denoising in linear domain via singular value decomposition (SVD)[J]. Oil Geophysical Prospecting, 2010, 45(2): 185-189. [本文引用:1]

1997

0.0

... 0 引言近年来,随着易开采资源的不断减少以及地表条件的复杂化,检波器接收到的地震信号的信噪比及分辨率越来越低^[1] ...

2006

0.0

. 2006, 21(2):546-553

An overview of the methods and techniques for seismic data noise attenuation

地震资料去噪方法技术综合评述

Zhang Jun-hua , Lv Ning , Tian Lian-yu

张军华, 吕宁, 田连玉

... F-K滤波是建立在二维傅里叶变换基础上的处理方法^[2] ...

2012

0.0

... -p变换又称倾斜叠加,它的实质是离散化的Radon变换,主要针对地震资料中的倾斜干扰^[3] ...

2012

0.0

. 2012, 34(1):85-96

A study on method of signal denoising based on wavelet transform for micro-seismicity monitoring in large-scale rockmass structures

基于小波变换的大尺度岩体结构微震监测信号去噪方法研究

Xu Hong-bin , Li Shu-lin , Chen Ji-jing.

徐宏斌, 李庶林, 陈际经

... 基于多尺度分析的小波变换方法采用传统小波变换,将地震资料分解到不同的尺度并设置相应的阈值,以求得到压制噪声的效果^[4] ...

2012

0.0

. 2012, 31(2):25-27 DOI:doi:10.3969/j.issn.1674-7720.2012.02.010

A multi-scale method for image denoising based on Ridgelet transform

基于Ridgelet变换的多尺度去噪算法研究

Wang Mei , Hou Zhen-jie , Lv Guo-ling

王梅, 侯振杰, 吕国玲

给出了Ridgelet变换的理论,并提出了一种基于尺度因子与Ridgelet变换的图像去噪算法,将Ridgelet应用于图像去噪并与小波去噪进行比较。实验结果表明,该算法对高斯白噪声污染的图像去噪具有较好的效果,不仅可以提高处理图像的信噪比,而且图像的视觉效果有明显改善。

... 例如Ridgelet变换^[5]、Curvelet变换^[6]、Contourlet变换^[7]、Shearlet变换^[8]等 ...

2002

0.0

... 例如Ridgelet变换^[5]、Curvelet变换^[6]、Contourlet变换^[7]、Shearlet变换^[8]等 ...

2014

0.0

. 2014, 49(4):739-744

Multi attribute fusion method for seismic signal based on contourlet transform

基于Contourlet 变换的地震多属性融合方法

Xie Cheng-fang , Peng Zhen-ming , Zhou Jing-jing

谢成芳, 彭真明, 周晶晶

... 例如Ridgelet变换^[5]、Curvelet变换^[6]、Contourlet变换^[7]、Shearlet变换^[8]等 ...

2010

0.0

... 例如Ridgelet变换^[5]、Curvelet变换^[6]、Contourlet变换^[7]、Shearlet变换^[8]等 ...

2015

0.0

. 2015, 45(6):2043-2048 DOI:doi:10.13229/j.cnki.jdxbgxb201506044

Frequency-domain regularized wiener filtering for seismic random noise suppression

基于频域正则维纳滤波的地震随机噪声压制

Tian Ya-nan , Li Yue , Lin Hong-bo

田雅男, 李月, 林红波

摘　要：在原始目标函数基础上,通过构建附加噪声约束项和正则因子的约束函数的方式,提出了一种频域正则维纳滤波,同时引入信号幅度调节因子,在控制噪声压制强度的同时调节由滤波造成的有效信号损失幅度。此外,利用初至前噪声和含噪记录共同实现随机噪声的谱估计。仿真记录和实际数据的试验结果表明,新算法的滤波效果比中值滤波和传统维纳滤波效果好,信号偏差及有效信号衰减少,验证了新方法正则化思想的可行性和有效性。

... 另一方面,在强噪声低信噪比条件下,传统维纳滤波会导致有效信号幅度的衰减严重^[9] ...

2010

0.0

. 2010, 45(2):185-189

Seismic wave field separation and denoising in linear domain via singular value decomposition (SVD)

频域奇异值分解(SVD)地震波场去噪

Shen Hong-yan , Li Qing-chun.

沈鸿雁, 李庆春

无规则干扰噪声的频谱分带较宽，不存在相干性；但在同一地区地震信号的主频带区间大致相同,尤其是叠后数据，也就是说各地震道有效频带的频谱存在较好的相干性。本文基于这个特点，通过傅里叶变换，在频率域进行SVD变换，并设计滤波因子，提取目标信号的奇异值进行重构频域信号，然后再进行反傅里叶变换，实现地震波场分离与去噪。与传统的带通滤波相比，该方法能彻底压制主频带干扰噪声，保护高、低频有效信号。实际地震数据处理表明，在不破坏原始地质信息的前提下，能较好地提高地震信号的信噪比。

... 在频率域,不同道的地震信号具有相同的有效频带,即各地震道有效频带的频谱存在较好的相干性,满足低秩条件,而噪声是随机的,频带较宽^[10] ...