作者简介:江海宇(1987-),男,博士,在站博士后.研究方向:油田压裂微地震监测.E-mail:jianghy12@mails.jlu.edu.cn
在监测工区范围内建立一个可用速度模型能够有效地提高微地震定位的可信度,本文针对微地震地面监测速度模型校正进行研究。目前已有的微地震地面监测速度模型校正方法仅对各层速度不确定性进行了分析,并没有考虑到各层界面位置不确定性,导致最终射孔定位结果仍存在一定误差。本文在振幅叠加微地震速度模型构建方法基础上,提出了通过扩大解空间的方法提高射孔重定位精度,即在极快速模拟退火方法过程中同时考虑各层速度不确定性和层界面位置不确定性。二维层状起伏地层模型实验表明:与现有方法相比,该方法能够准确将射孔事件重定位至其真实值处,并能有效提高射孔点附近微地震事件定位可信度。最后将该方法应用于实际野外数据处理,验证了该方法的有效性和实用性。
The existing method of velocity optimization for surface monitoring only considers the velocity uncertainty of each layer, which bring certain errors in the results of perforation shot relocation. A new method of expanding the solution space on the basis of amplitude stacking is proposed to improve the accuracy of perforation shot localization. In the process of every fast simulated annealing, the velocity uncertainty and location uncertainty of each layer are considered simultaneously. Synthetic data test shows that, compared with the existing method, the proposed method can accurately locate the perforating shot to its actual value, and can effectively improve the location reliability of microseismic events near the perforation. This new method is applied to actual field data processing, and its validity and practicability are verified.
微地震定位技术是水压致裂工作的核心[1, 2, 3], 该技术实施过程中, 裂缝延伸导致周围岩石破裂, 从而引发一系列可观测记录的微地震事件[4]。而监测工区范围内地下速度模型是影响微地震事件定位准确与否的主要因素, 因此, 如何获得一个有效的速度模型是微地震监测工程的关键性问题[5]。
在微地震监测工程中, 地震层析成像方法是寻求地下速度结构的有效手段, 但在实际压裂监测过程中受条件制约, 射孔信息量较少, 地面检波器数量及覆盖范围严重不足, 获得较为精细的工区地下速度结构几乎是不可能的。目前现有的微地震速度模型构建方法都以射孔重定位精度作为评判依据。Anikiev等[6]采用尝试的办法, 同时对各层测井初始模型进行同时增加或减小一定值, 得到一个相对较准确的反演速度模型。Pei等[7]采用Occam法进行地下速度模型反演, 谭玉阳等[8]采用Levenberg-Marquardt方法进行速度模型反演。Pei等[9]、Jiang等[10]采用极快速模拟退火方案进行速度模型校正, 取得了一定效果。但以上方法均依赖于射孔记录的初至拾取, 在低信噪比情况下该方法失效。江海宇[11]提出基于振幅叠加地面观测微地震速度模型校正方法, 有效解决了上述问题。但该方法仅考虑到各层速度不确定性, 而并没有考虑到各层界面位置不确定性, 导致射孔重定位仍存在一定误差。
本文在振幅叠加地面观测微地震速度模型校正方法的基础上, 在极快速模拟退火方法过程中同时考虑各层速度不确定性, 以及层界面位置不确定性, 通过扩大解空间的方法提高射孔事件重定位精度。该方法能够有效克服现有的微地震地面速度模型校正缺陷。文中首先介绍了该方法原理, 然后对合成数据进行分析计算并与原算法进行分析对比, 从而证明了该方法的有效性。
振幅叠加地面观测微地震速度模型校正算法思想主要来源于微地震振幅叠加定位算法[11, 12, 13, 14, 15], 该方案不需要拾取震相初至信息, 通过监测射孔点处能量聚焦情况, 并以射孔点重定位精度, 判定速度模型是否可用于后续微地震定位。该方法能够有效抑制地面噪声干扰, 其方法原理如下:
(1)以射孔点位置作为中心点, 定义一个足够大的目标区域, 根据定位精度需要将其划分为若干大小相同的网格, 每个网格的中心点可看作是某个微地震事件潜在发生位置。
(2)根据声波测井先验信息获得初始速度模型, 在该速度模型下, 遍历所设目标区域所有网格中心点, 并根据网格逐次剖分微地震定位方法获得该区域内能量聚焦最大值
(4)以速度值作为不确定因素, 采用极快速模拟退火法对目标层进行速度调整, 并以实际射孔点位置处能量聚焦值作为极快速模拟退火方法中的目标函数
(5)模拟退火算法结束后, 还需对射孔事件进行重定位, 以验证速度模型的有效性, 如果定位误差较大, 还需进行回火处理。调整速度模型, 直到定位误差足够小为止。
第i道与参考道在第j层的走时之差为:
式中:Δ lij为第i道与参考道在第j层的路径差; vj为第j层波速, 属于该算法中的不确定因素。
设各道波形在第j时刻的振幅值为A(f(t), k), 那么各道检波器波形根据Δ ti逆时偏移后, 振幅叠加表达式为:
将
从式(3)中可以看出, 影响振幅叠加结果的主要是第
式中:
式中:sgn为符号函数, μ ∈ [0, 1]; Tk 为退火降温参数, Tk=T0 exp(-ck1⁄2 N), 其中, T0 为初始退火温度; c为给定常量调整退火温度, c=0.5; N为需要调整速度层数。
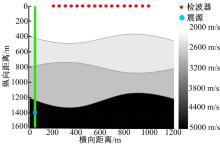
选择二维层状起伏结构地层模型进行验证本文的改进算法, 实际信号采用有限差分波动方程进行模拟, 根据所模拟的地层模型建立初始平层状地层模型, 后续的正演采用射线追踪方法[16], 反演方法采用上述振幅叠加速度模型校正方法, 并加入本文所提出的层界面位置不确定因素, 本次实验假定中间各层界面上下浮动不超过50 m。检波器排布、震源以及监测井位置如图1所示。
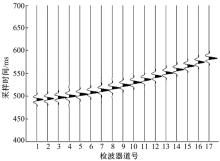
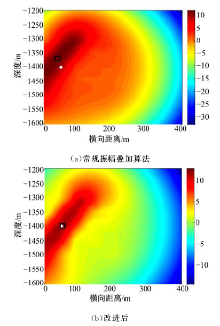
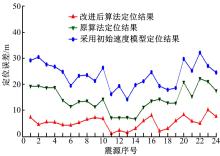
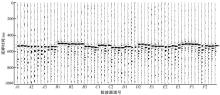
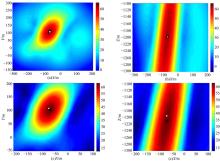
图1中, 首个检波器坐标为(200, 0), 每个检波器间距为50 m, 震源位置为(50, 1400)。表1为根据测井曲线建立的初始速度模型参数。图2为各道检波器正演模拟波形。利用常规振幅叠加速度模型构建算法得到的射孔重定位结果误差为23 m左右(图3(a)所示), 而采用本文改进后的算法重定位误差小于2 m(图3(b)所示), 可见本文改进后的算法比常规算法更优。为验证该方法对震源定位可信度的提高效果, 本文在射孔周围设置了24个震源(图4所示), 分别采用初始速度模型, 原振幅叠加微地震速度模型校正算法, 以及改进后速度模型校正方法构建速度模型, 并对24个震源进行重定位处理, 定位分布结果如图4所示, 震源定位分布误差如图5所示。从以上结果可以看出, 采用本文方法进行速度模型校正后, 能够有
| 表1 根据测井曲线建立的平层结构模型 Table 1 Flat-layerd model established by logging curve |
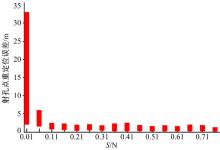
效提高射孔周边微地震定位可信度。图6为在不同信噪比的情况下, 采用本文算法进行速度模型校正后, 射孔重定位误差分布示意图。图中粗线表示进行100次试验后定位误差范围。信噪比定义如下[17]。
式中:
从图3中可以看出, 由于本文算法采用了振幅叠加算法进行计算, 因此, 本文算法对噪声干扰具有较强的抑制作用。
将本文方法应用于山西宁武盆地武2-2井一次煤层气压裂监测, 本次压裂监测共放置A-F六条测线, 共60道地面单分量检波器。每条测线首个检波器距离压裂井中心至少200 m的距离。避免了地面施工带来的噪声干扰, 同时保证各道检波器之间距离均匀。进行射孔操作的直井井口位于整个观测系统中心, 在统一系统坐标下, 施工井口坐标为(-24.133, 112.56, -1.34)(单位:m), 射孔深度为-1197.8 m, 射孔位置(压裂点坐标)为(-68.025, 107.258, -1197.8)(单位:m)。目标区域划分范围为
| 表2 初始速度模型参数 Table 2 Parameters of initial velocity model |
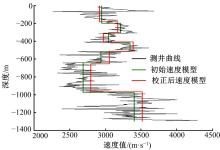
首先根据测井曲线获得平层状初始模型, 利用本文方法对速度模型进行校正, 并分别利用本文改进后的算法与原算法校正后的速度模型对射孔事件进行重定位, 射孔定位结果如图8所示, 图8(a)(b)为经过本文改进后射孔重定位结果; 图(c)(d)为采用常规振幅叠加速度模型校正算法射孔重定位结果。速度模型反演结果如图9所示, 采用本文改进后的算法定位结果为(-69, 107.5, -1196), 射孔点重定位误差仅为1.5 m, 而原算法校正后射孔点重定位结果为(-65.1, 112.1, -1210.9), 距离射孔点距离13.5 m。从实际数据处理结果上来看, 本文方法更有效地消除射孔点重定位误差。
常规的振幅叠加速度模型构建方法, 由于仅考虑到各层速度不确定性, 而没有考虑各层界面位置不确定性, 因此模拟退火算法过程中速度模型解空间较小, 导致射孔重定位仍存在一定误差。本文提出在原算法模拟退火计算过程中加入各层界面位置不确定因素, 通过增大解空间的方式提高射孔点重定位精度, 模型试验及野外实际数据处理表明, 通过本文方法进行改进后, 能够很好的解决射孔重定位不准的问题, 并有效提高射孔点周围微地震定位可信度。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|