基于改进粒子滤波的煤矿视频监控模糊目标检测

引用本文

杨超宇, 李策, 梁胤程, 杨峰. 基于改进粒子滤波的煤矿视频监控模糊目标检测[J].吉林大学学报（工学版）, 2017,47(6): 1976-1985
YANG Chao-yu, LI Ce, LIANG Yin-cheng, YANG Feng. Blurred object detection based on improved particle filter in coal mine underground surveilance[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1976-1985 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706041
Permissions

基于改进粒子滤波的煤矿视频监控模糊目标检测

杨超宇^1,², 李策¹, 梁胤程¹, 杨峰¹

1.中国矿业大学(北京) 机电与信息工程学院,北京 100083

2.安徽理工大学经济与管理学院,安徽淮南 232001

作者简介:杨超宇(1981-),男,副教授,博士.研究方向:计算机视觉,图像分析,多媒体物联网.E-mail:yangchy@aust.edu.cn

基金:国家自然科学基金项目(51404007,61601466); 安徽省重大教学改革研究项目(2015zdjy074)

摘要

针对煤矿井下智能视频监控采集到的视频图像质量较差、干扰多、噪点多、目标检测不准确等问题,提出了一种基于改进粒子滤波的模糊目标检测方法。在标准粒子滤波理论框架下,以视频多图像帧差为基础构建非线性、非高斯多系统状态空间融合模型;在图像帧差得到的关键点区域范围内进行粒子抽样及概率密度的传播;利用加权后验样本粒子表示多系统状态空间融合模型的后验概率密度;采用样本均值方法融合估计系统后验状态;最后对系统状态空间模型进行输出,得到目标检测结果。使用三交河煤矿井下视频监控数据进行试验验证,分别釆用改进的粒子滤波、标准粒子滤波、无损卡尔曼滤波以及扩展卡尔曼滤波等方法进行对比。试验结果表明:针对煤矿井下视频模糊目标检测问题,改进的多状态空间模型及关键区域采样粒子滤波算法具有良好的目标检测效果。

关键词: 信息处理技术; 目标检测; 粒子滤波; 多状态空间; 关键区域采样

中图分类号:TD76 文献标志码:A 文章编号:1671-5497(2017)06-1976-10

Blurred object detection based on improved particle filter in coal mine underground surveilance

YANG Chao-yu^1,², LI Ce¹, LIANG Yin-cheng¹, YANG Feng¹

1.School of Mechanical Electronic and Information Engineering, China University of Mining and Technology(Beijing), Beijing 100083, China

2.School of Economics and Management, Anhui University of Science and Technology, Huainan 232001, China

Abstract

Regarding that the videos collected by intelligent monitoring system in coal mine underground are blur, a novel algorithm for unclear video object detection based on improved particle filter is proposed. In the framework of standard particle filter, a nonlinear, non-Gaussian and multi system state space fusion model is constructed based on frame difference. First, particle sampling and probability density propagation are realized in the region of the key points obtained in the frame difference image. Then, the weighted posterior sample particles are used to represent the posterior probability density of the multi system state space fusion model. The mean of the samples is used to estimate and fuse the posteriori state of the system. Finally, the system state space model is output to fulfill the object detection. Experiments are carried out using the video data of the Sanjiaohe coal mine underground monitoring system. The performance of the proposed model is evaluated by comparison with extended Kalman filter, unscented Kalman filter and particle filter. The improved accuracy and effectiveness of the proposed method are demonstrated.

Keyword: information processing technology; object detection; particle filter; multi-state space; critical region sampling

Show Figures

煤矿智能视频监控系统能够改变以往人工监控的模式, 自动分析理解视频画面中的内容, 发现监控场景中存在的异常行为、可疑目标和潜在危险, 迅速发出实时警报, 从而指导启动相应的联动控制措施^{[1, 2, 3]}。

本文针对煤矿井下智能视频监控系统这一特定的应用场合, 考虑光照较暗、井下粉尘大、探照强光干扰多造成的模糊和噪声现象^{[4, 5]}, 在低信噪比条件下进行井下目标的实时检测和跟踪, 提出了一种基于多状态空间及关键区域采样粒子滤波的井下目标自动检测方法。

1 模糊目标检测系统模型

粒子滤波(Particle filter, PF)算法也称为序列化蒙特卡洛方法(Sequential Monte-Carlo methods, SMCM), 该方法的基本思想是通过随机粒子抽样传播概率密度, 用一组带有权值的随机采样粒子表示系统状态的后验概率密度(Posterior probability density function, PDF), 并利用该粒子集以样本均值方法计算当前系统状态的估计值^[6], 不但避免了对目标状态矩阵的积分运算, 而且为解决非线性、非高斯动态系统中的目标检测及跟踪问题提供了一种简便、有效的方法^{[7, 8]}。

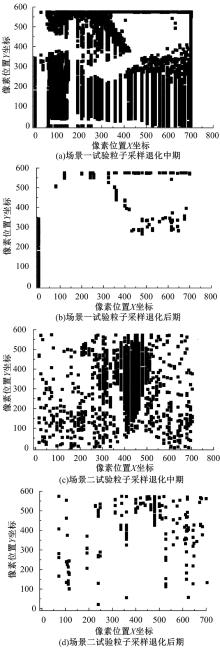
传统的粒子滤波方法, 仅考虑视频序列中某一帧的状态特征, 在一帧中进行粒子采样、预测更新状态量、递归估计后验概率密度、估计输出状态量等计算操作。但实际中视频序列目标的检测识别与上下文环境紧密相关, 因此仅考虑一帧的状态量, 将关键的时间序列上下文信息丢弃, 会严重影响目标检测的效果。尤其是在煤矿井下的特殊环境中, 视频监控采集到的图像信息较为模糊、噪声大, 更需要视频前、后多帧图像信息的检测辅助支持。其次, 粒子滤波采样时会在当前图像帧全部范围内进行特征采样, 没有对检测目标的重点范围进行标定, 检测目标时容易出现误检的情况。在井下视频监控中, 视频采集设备是固定的, 井下动态目标出现的范围是有限的。因此, 将粒子采样范围划定在目标出现可能性较大的区域内, 更容易准确地检测到目标。

本文从状态估计的角度分析煤矿井下模糊目标分割问题, 建立基于时间序列的多状态模型, 利用Bayesian迭代和逐次求精机制, 求解问题相对应的多状态空间转移模型及观测模型。将视频序列中获取的帧差图像做为关键点区域, 通过在关键点区域内进行粒子采样, 缩小目标检测范围, 能够更加准确、快速地检测到目标。最后, 采用样本均值方法进行多模型融合, 得到检测结果。构建的目标检测系统模型如图1所示。

	Figure Option View Download New Window
	图1 目标检测系统模型Fig.1 Model of object detection system

视频目标检测的任务在粒子滤波框架下转化为在视频序列中使用观测数据推理出检测目标的空间状态的问题, 即在时变动态系统中估计状态空间参数, 状态推理框架中包括两种模型^{[9, 10]}:①动态模型, 描述目标状态在时间维上的演变过程; ②观察模型, 在离散的时间上获取包括噪声数据的观察状态与目标实际状态的关联。在 $\begin{matrix} k \end{matrix}$ 时刻, 取煤矿监控视频中当前帧的前N帧 $\begin{matrix} \overset{N}{⋃_{n = 1}} \end{matrix}$ frm_k, 分别对相邻两帧做帧差计算, 得到k时刻前N帧的帧差集 $\begin{matrix} \overset{N - 1}{⋃_{n = 1}} \end{matrix}$ dif_k_,_n, 对每个帧差结果都建立一个状态空间模型, 设 $\begin{matrix} N \end{matrix}$ 个非线性动态系统的状态空间模型为:

$x_{k, n} = f_{k, n} (x_{k - 1, n}, v_{k - 1, n}) n \in {1, 2, \dots N} (1)$

$z_{k, n} = h_{k, n} (x_{k, n}, u_{k, n}), n \in {1, 2, \dots N} (2)$

式中: $\begin{matrix} x_{k, n} = {x_{0, n}, x_{1, n}, \dots, x_{k, n}} \end{matrix}$ 为 $\begin{matrix} k \end{matrix}$ 时刻的第 $\begin{matrix} n \end{matrix}$ 个系统状态; $\begin{matrix} z_{k, n} = {z_{0, n}, z_{1, n}, \dots, z_{k, n}} \end{matrix}$ 为 $\begin{matrix} k \end{matrix}$ 时刻第 $\begin{matrix} n \end{matrix}$ 个观测数据; $\begin{matrix} f_{k, n} : R^{x} \to R^{x + 1} \end{matrix}$ 为系统状态转移函数; $\begin{matrix} h_{k, n} : R^{x} \to R^{x + 1} \end{matrix}$ 为系统观测函数; $\begin{matrix} v_{k, n} \end{matrix}$ 和 $\begin{matrix} u_{k, n} \end{matrix}$ 分别为系统演化过程噪声和观测噪声。

依据粒子滤波解决框架, 设系统演变过程为马尔可夫过程, 目标检测就是根据有噪声观测值, 递归估计出非线性系统状态的后验概率密度, 并且采用样本均值的方法对多个系统状态的后验概率密度进行融合, 其计算公式为:

$\begin{matrix} \overset{N}{\sum_{n = 1}} p (x_{k, n} | z_{k, n}) \end{matrix}$

通过贝叶斯参数估计进行目标检测, 对于稳定随机过程, 从观察数据z_{k, n}中推理k时刻第n个系统状态值x_{k, n}, 构建后验概率密度函数 $\begin{matrix} p (x_{k, n} | z_{k, n}) 。 \end{matrix}$ 通过先验知识得到 $\begin{matrix} p (x_{0} | z_{0}) \end{matrix}$ 初始概率密度函数, 通过两步递归运算得出 $\begin{matrix} p (x_{k, n} | z_{k, n}) \end{matrix}$ 的预测步骤和更新步骤为:

$\begin{matrix} p (x_{k,, n} | z_{k - 1, n}) = \frac{p (z_{k, n} | x_{k, n}) p (x_{k, n} | z_{k, n})}{p (z_{k, n} | z_{k - 1, n})} (3) \end{matrix}$

式中: $\begin{matrix} p (z_{k, n} | z_{k - 1, n}) \end{matrix}$ 为归一化常数:

$\begin{matrix} \begin{matrix} p (z_{k, n} | z_{k - 1, n}) = \\ \int p (z_{k, n} | x_{k, n}) p (x_{k, n} | z_{k - 1, n}) d x_{k, n} (4) \end{matrix} \end{matrix}$

最优贝叶斯估计的一般表达形式由上述预测和更新步骤给出, 在约束条件下, 采用卡尔曼滤波方法计算最优贝叶斯解。在贝叶斯最优估计框架下, 许多非线性问题的求解都要求计算高维积分, 基于随机采样运算的蒙特卡罗方法可以模拟贝叶斯估计求解问题^{[11, 12]}。

2 模糊目标检测算法实现

为了验证本文算法的有效性, 对取自三交河煤矿井下的两组监控视频数据进行分析, 如图2和图3所示。场景一为副井下口出口视频, 该视频帧高度为576像素, 帧宽度为704像素, 帧速率为15帧/s, 比特率为2048 kbit/s。场景二为煤矿井下皮带机传送视频数据, 该视频帧高度为576像素, 帧宽度为720像素, 帧速率为30帧/s, 比特率为1024 kbit/s。视频图像由于受到井下光照及雾尘噪声等因素的影响, 图像场景模糊不清。

	Figure Option View Download New Window
	图2 场景一试验Fig.2 Experiments on first scenario

	Figure Option View Download New Window
	图3 场景二试验Fig.3 Experiments on second scenario

2.1 粒子采样

设系统状态 $\begin{matrix} x_{k, n} \end{matrix}$ 服从一阶Markov过程, $\begin{matrix} x_{k, n} \end{matrix}$ 与系统观测值 $\begin{matrix} z_{k, n} \end{matrix}$ 相互独立^[13]。在系统初始状态 $\begin{matrix} x_{0, n} \end{matrix}$ 下, 从先验分布 $\begin{matrix} p (x_{0}) \end{matrix}$ 中抽取出 $\begin{matrix} M \end{matrix}$ 个独立同分布样本 $\begin{matrix} {\{x_{i}\}}^{M} 。 \end{matrix}$

因为视频开始前 $\begin{matrix} N \end{matrix}$ 帧无法再往前取视频帧, 所以前 $\begin{matrix} N \end{matrix}$ 帧在视频帧全范围中抽取样本。此处 $\begin{matrix} N \end{matrix}$ 的值设为10。在第10帧以后, 粒子采样的范围缩小为前 $\begin{matrix} N \end{matrix}$ 帧相邻帧差计算得到的关键区域。帧差计算结果如图2和图3中(d)~(f)所示。 $\begin{matrix} k \end{matrix}$ 时刻的关键区域设定为当前帧的前 $\begin{matrix} N \end{matrix}$ 相邻帧差的并集 $\begin{matrix} K A_{k} \end{matrix}$ , 如式(5)所示, 并且将帧差处理结果用图像形态学的腐蚀膨胀处理, 使得到的目标范围闭合, 从而能保证粒子采样时不会漏掉目标出现区域, 如图4所示。

$\begin{matrix} \begin{matrix} K A_{k} = (fr m_{k - 1} - fr m_{k - 2}) ⋃ (fr m_{k - 2} - fr m_{k - 3}) \\ ⋃ \dots ⋃ (fr m_{k - n + 2} - fr m_{k - n + 1}) (5) \end{matrix} \end{matrix}$

在煤矿井下视频监控中, 目标出现的范围是有限的, 视频监控画面中很大一部分是无效的背景区域。在井下光线较弱环境中, 目标检测时易将目标有限出现区域与周围环境混淆。通过在关键区域内采样, 能缩小目标检测范围, 去除视频中无效的背景区域, 既能提高采样效率, 也能更加准确地检测到视频目标。图5为根据帧差并集获得的粒子采样区域分布图, 由于视频帧的原点坐标在屏幕左上角, 而分布图原点坐标在左下角, 所以粒子采样区域分布图与帧差并集上下方向相反。

	Figure Option View Download New Window
	图4 帧差并集Fig.4 Union of frame difference

	Figure Option View Download New Window
	图5 粒子采样范围分布Fig.5 Range and distribution of particle sampling

2.2 粒子加权

多状态模型粒子采样系统PDF用经验分布逼近为:

$\begin{matrix} q (x_{k, n} | z_{k, n}) = \frac{1}{M} \overset{M}{\sum_{i = 1}} δ (x_{k, n} - x_{k, n}^{i}) (6) \end{matrix}$

式中: $\begin{matrix} δ (\cdot) \end{matrix}$ 为狄拉克 $\begin{matrix} δ \end{matrix}$ 函数, 此时对建立的多个系统状态模型进行样本均值融合计算:

$\begin{matrix} q (x_{k} | z_{k}) = \frac{1}{N} \overset{N}{\sum_{n = 1}} q (x_{k, n} | z_{k, n}) (7) \end{matrix}$

在定义的井下模糊目标检测状态空间中, 式(7)能够得到方便于随机抽样的条件概率分布, 具有更大的支撑集。

当井下视频监控观测序列数据到达时, 在 $\begin{matrix} k \end{matrix}$ 时刻从 $\begin{matrix} q (x_{k} | x_{k}^{i}, z_{k}) \end{matrix}$ 中抽取 $\begin{matrix} x_{k, n}^{i} \end{matrix}$ 。在实际随机采样过程中, $\begin{matrix} p (z_{k} | x_{k - 1}^{i}) \end{matrix}$ 使用先验概率分布函数:

$\begin{matrix} q (x_{k}^{i} | x_{k - 1}^{i}, z_{k}) = p (x_{k} | x_{k - 1}) (8) \end{matrix}$

依据迭代计算得到任一时刻随机抽取粒子的权重值, 根据贝叶斯公式有:

$\begin{matrix} \begin{matrix} ω_{k}^{i} = ω_{k - 1}^{i} \frac{p (z_{k} | x_{k}^{i}) p (x_{k}^{j} | x_{k - 1}^{j})}{q (x_{k}^{i} | x_{k}^{i}, z_{k})} = \\ ω_{k - 1}^{i} \frac{p (z_{k} | x_{k}^{i}) p (x_{k}^{j} | x_{k - 1}^{j})}{q (x_{k}^{i} | x_{k}^{i}, z_{k})} = \\ ω_{k - 1}^{i} p (z_{k} | x_{k - 1}^{i}) (9) \end{matrix} \end{matrix}$

根据式(9), 获得重要性权值的计算结果为:

$\begin{matrix} ω_{k}^{i} = ω_{k - 1}^{i} p (z_{k} | x_{k - 1}^{i}) (10) \end{matrix}$

在计算重要性权重并归一化之后, 得到一组加权的粒子 $\begin{matrix} {x_{k}^{i}, ω^{i}; i = 1, 2, \dots, M}, \end{matrix}$ 当粒子数量足够多时, 后验概率密度的加权估计可以逼近系统真实分布状态。

2.3 状态估计输出

当迭代到第k步时, k时刻的系统状态后验分布p(x_k |z_k)能够由加权粒子集 $\begin{matrix} {x_{k}^{i}, ω_{k}^{i}} \end{matrix}$ 近似表示^[14], 视频帧系统目标状态 $\begin{matrix} x_{k} \end{matrix}$ 的最小均方误差估计为:

$\begin{matrix} {\hat{x}}_{k} = E (x_{k} | z_{k}) \approx \overset{M}{\sum_{i = 1}} ω_{k}^{i} x_{k}^{i} (11) \end{matrix}$

最大后验估计为:

$\begin{matrix} {\hat{x}}_{k} = \underset{x_{k}}{\arg \max} [p (x_{k} | z_{k})] \approx \underset{x_{k}}{\arg \max} ω_{k}^{i} (12) \end{matrix}$

2.4 重要性重采样

粒子滤波算法最难解决的是权值退化问题, 当经过若干次迭代以后, 可能只有很少数的粒子具有重要性权值, 最终的情况会变成只有一个粒子的权值趋近于1, 其他粒子权值越来越小, 甚至忽略不计。这个问题会增加大量的计算时间, 但是对系统状态的估计不起任何作用, 降低了算法性能^[15]。解决权值退化的常用方法是重要性重采样方法^[16], 它是对随机采样粒子和表示其相应权值的概率密度函数进行重新采样, 将权值较小的粒子删除, 增加权值较大的粒子, 重新得到一组新的粒子样本。经过重要性重采样以后, 粒子的分布最后会与目标概率分布基本一致。

本文方法在关键区域 $\begin{matrix} K A_{k} \end{matrix}$ 内进行均匀抽样, 产生 $\begin{matrix} M \end{matrix}$ 个随机数, 将随机数属于关键区域中某一子区域对应的粒子复制为新粒子集中的粒子, 从而完成新粒子集的采样, 重采样过程中权值越大的粒子其对应的空间区域越大, 被复制为新粒子的概率就越大。如果在全部区域内进行粒子集重采样, 则重采样的范围过大, 容易采集到无效的粒子样本集, 粒子权值退化更快, 粒子集重采样退化如图6所示。

	Figure Option View Download New Window
	图6 粒子采样区域退化Fig.6 Degradation of particle sampling region

2.5 算法流程

步骤1 粒子集初始化。

获取视频中前面 $\begin{matrix} N \end{matrix}$ 帧图像, 依据帧差法得到多帧运动模糊目标的前景像素点分布值。在 $\begin{matrix} k = 0 \end{matrix}$ 时刻, 根据系统状态的先验分布 $\begin{matrix} p (x_{0}), \end{matrix}$ 初始化系统状态粒子集 $\begin{matrix} {x_{0}^{i}, ω_{0}^{i}}, \end{matrix}$ 其中, $\begin{matrix} ω_{0}^{i} = 1 / P 。 \end{matrix}$

步骤2 采样并计算权值。

获取到新的监控视频帧之后, 计算更新前 $\begin{matrix} N \end{matrix}$ 帧的帧差, 在帧差范围内进行粒子采样, 根据粒子滤波预测各像素点的前景目标分布概率。分别取 $\begin{matrix} k = 1, 2, \dots, M, \end{matrix}$ 依次从状态转移概率 $\begin{matrix} p (x_{k}^{i} | x_{k - 1}^{i}) \end{matrix}$ 抽取随机粒子, 得到新的粒子集 $\begin{matrix} {{\tilde{x}}_{k}^{i}} 。 \end{matrix}$ 根据式(9)计算 $\begin{matrix} {\tilde{x}}_{k}^{i} \end{matrix}$ 的权值 $\begin{matrix} {\tilde{ω}}_{k}^{i}, \end{matrix}$ 并根据式(10)进行归一化。

步骤3 状态估计输出。

依据粒子集 $\begin{matrix} {{\tilde{x}}_{k}^{i}, ω_{k}^{i}}, \end{matrix}$ 由式(8)计算系统状态后验概率分布 $\begin{matrix} p (x_{k} | z_{k}) 。 \end{matrix}$ 像素最终属于前景或背景的概率分布值, 即系统最终状态估计可以由式(11)(12)计算得到, 计算结果作为图像分割的依据。

步骤4 重采样。

根据粒子的权值 $\begin{matrix} ω_{k}^{i} \end{matrix}$ 大小排序, 去除P个较小权值粒子, 从粒子集 $\begin{matrix} {{\tilde{x}}_{k}^{i}, ω_{k}^{i}} \end{matrix}$ 中重新抽取P个粒子 $\begin{matrix} {x_{k}^{i}}, \end{matrix}$ 同时令 $ω_{k}^{(i)} = 1 / P$ , 得到新的粒子集 $\begin{matrix} {x_{k}^{i}, 1 / P} 。 \end{matrix}$

步骤5 循环继续。

$\begin{matrix} k \end{matrix}$ 值加1, 返回到步骤2继续执行。

3 试验及结果分析

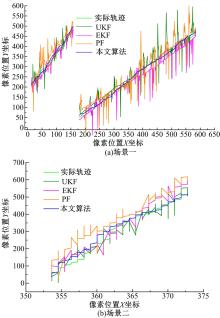
分别采用扩展卡尔曼滤波(Extended Kalman filter, EKF)、无损卡尔曼滤波(Unscented Kalman filter, UKF)、标准粒子滤波(Particle filter, PF)和本文算法4种算法对实际采集的视频数据进行目标检测试验, 试验数据为第2节所描述的两段煤矿井下监控视频数据, 如图2(a)(b)(c)、图3(a)(b)(c)所示, 试验程序在Windows系统下的Visual Studio 10平台上使用OpenCV2.49库运行。通过试验结果比较4种算法的目标检测效果和目标检测误差、运行时间效率等, 分析各种算法的优劣。

在煤矿井下监控视频序列条件下, 赋予权值的粒子集对目标检测近似, 通过随机位置对粒子进行初始化估计, 利用平均相等的先验权值, 在检测运动目标过程中对目标信息进行更新, 标定新的目标位置和检测结果, 粒子通过状态空间转移模型进行演化, 相应的权值被考虑为相应粒子的似然函数, 从下一帧的图像中检测到目标图像。算法中主要设定的状态参量包括位置、速度、加速度等信息, 位置状态 $\begin{matrix} x ~ U [0, n_{x}], y ~ U [0, m_{y}]; \end{matrix}$ 速度状态 $\begin{matrix} (x, y) ~ U [- 1, 1]; \end{matrix}$ 强度状态 $\begin{matrix} I ~ U [10, 30] 。粒子总数 N = 1000, \end{matrix}$ 有效粒子门限N_s=500, p=4。

图7和图8分别为使用4种算法对视频帧图像进行目标检测的运行结果。其中, 图7(a)(b)和图8(a)(b)显示了使用EKF算法和UKF算法进行煤矿井下视频目标检测的运行结果, 可以看到:场景一中由于光照原因, 人员与运煤车目标出现反差较大,

	Figure Option View Download New Window
	图7 试验一目标检测结果Fig.7 First experimental results of object detection

	Figure Option View Download New Window
	图8 试验二目标检测结果Fig.8 Second experimental results of object detection

人员运动较亮而运煤车运动轨迹较为模糊, 因此算法无法将场景中两个目标同时清晰地检测出。场景二中由于光照较暗并且有粉尘, 因此并没有检测出皮带机上的运输煤目标, 甚至连运动的皮带也很难检测出来。图7(c)和图8(c)是采用PF算法分别在场景一和场景二中的处理效果, 从图中可以看出:算法能够检测出一部分运动目标, 但是由于粒子采样的不准确, 因此检测的目标像素错误率较高、误检率较高, 有丢失检测目标的情况。图7(d)和图8(d)是本文算法的检测结果, 在视频数据不清晰的情况下, 本文算法依然能够提取出目标信息, 有助于提高整个视频监控系统的检测和识别能力。

通过计算高斯混合模型结合手动标记方法给出运动目标真实的运动轨迹, 并采用欧式距离 $\begin{matrix} d = \sqrt[]{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}} \end{matrix}$ 来衡量几种目标检测算法的目标中心点检测误差, 其中, $\begin{matrix} (x_{1}, y_{1}) \end{matrix}$ 为运动目标实际中心点坐标, $\begin{matrix} (x_{2}, y_{2}) \end{matrix}$ 为跟踪方法测得的中心点坐标。分别计算比较两个场景中两种检测算法的中心点检测误差, 结果如表1和表2所示。目标真实点位置检测精确度曲线如图9(a)(b)所示, 从图中可以看出:本文算法具有较好的检测精度, 与真实点状态匹配度较高, 而其他几种算法检测的目标中心点偏移较大, 并且检测目标时有发散的情况。

表1 场景一目标中心跟踪误差对比 Table 1 Comparison of object center tracking error in first scenario

表2 场景二目标中心跟踪误差对比 Table 2 Comparison of object center tracking error in second scenario

	Figure Option View Download New Window
	图9 目标检测位置对比Fig.9 Comparison of object detection position

	Figure Option View Download New Window
	图10 目标检测正确率对比Fig.10 Comparison the accuracy of object detection accuracy

图10(a)和10(b)中分别显示了两个场景中4种算法的目标检出正确率对比结果, 比较了4种算法的目标检出误差像素值, 包括漏检目标像素和误检目标像素, 用于判断正确目标的检出情况。可以看出:本文算法在目标检测中, 误差像素数目保持在了较低的水平值, 每一帧的误差像素数目均小于50。而其他算法, 分别达到50以上甚至100以上, 而且在某些帧中, 由于目标的模糊性, 误检像素会经常达到数百个的极值, 表明在某些不清晰的视频帧中, 这些方法无法准确地检测出井下巷道中的模糊目标。

4 结束语

为了能够在煤矿智能视频监控系统中更好地检测出目标对象, 给后续目标行为分析提供可靠的基础, 本文提出了一种改进粒子滤波的煤矿井下视频模糊目标检测算法。通过试验对本文算法与几种常见目标检测跟踪算法的检测结果进行比较分析, 可以看出本文算法在煤矿井下复杂环境下具有很好的检测效果, 比其他算法的目标检出正确率高。但是本文算法目前还具有收敛性差、实时性低等缺陷, 后续研究工作将在这些方面进行改进。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	孙继平. 煤矿安全生产监控与通信技术[J]. 煤炭学报, 2010, 35(11): 1925-1929. Sun Ji-ping. Technologies of monitoring and communication in the coal mine[J]. Journal of China Coal Society, 2010, 35(11): 1925-1929. [本文引用:1]
[2]	孙继平, 陈伟, 王福增, 等. 矿井监控图像中空列车的识别[J]. 中国矿业大学学报, 2007, 36(5): 597-602. Sun Ji-ping, Chen Wei, Wang Fu-zeng, et al. Recognizing empty trainsin coalmine surveillance images[J]. Journal of China University of Mining & Technology, 2007, 36(5): 597-602. [本文引用:1]
[3]	厉丹. 视频目标检测与跟踪算法及其在煤矿中应用的研究[D]. 徐州: 中国矿业大学信息与控制工程学院, 2011. Li Dan. Research on object detection and tracking algorithm and its application in coal mine[D]. Xuzhou: School of Information and Control Engineering, China University of Mining and Technology, 2011. [本文引用:1]
[4]	张谢华, 张申, 方帅, 等. 煤矿智能视频监控中雾尘图像的清晰化研究[J]. 煤炭学报, 2014, 39(1): 198-204. Zhang Xie-hua, Zhang Shen, Fang Shuai, et al. Clearing research on fog and dust images in coalmine intelligent video surveillance[J]. Journal of China Coal Society, 2014, 39(1): 198-204. [本文引用:1]
[5]	杜明本, 陈立潮, 潘理虎. 基于暗原色理论和自适应双边滤波的煤矿尘雾图像增强算法[J]. 计算机应用, 2015, 35(5): 1435-1438. Du Ming-ben, Chen Li-chao, Pan Li-hu. Enhancement algorithm for fog and dust images in coal mine based on dark channel prior theory and bilateral adaptive filter[J]. Journal of Computer Applications, 2015, 35(5): 1435-1438. [本文引用:1]
[6]	王法胜, 鲁明羽, 赵清杰, 等. 粒子滤波算法[J]. 计算机学报, 2014, 37(8): 1679-1694. Wang Fa-sheng, Lu Ming-yu, Zhao Qing-jie, et al. Particle filter algorithm[J]. Chinese Journal of Computers, 2014, 37(8): 1679-1694. [本文引用:1]
[7]	Kitagawa G. Monte Carlo filter and smoother for non-Gaussian non-linear state space models[J]. Journal of Computational and Graphical Statistics, 1996, 5(1): 1-25. [本文引用:1]
[8]	Gordon N, Salmond D. Novel approach to non-linear and non-Gaussian Bayesian state estimation[J]. Proc of Institute Electric Engineering, 1993, 140(2): 107-113. [本文引用:1]
[9]	吴刚. 基于粒子滤波与增量学习的车辆跟踪方法硏究[D]. 南京: 南京理工大学计算机学院, 2014. Wu Gang. Research of vehicle tracking methods based on particle filter and incremental learning[D]. Nanjing: College of Computer, Nanjing University of Science and Technology, 2014. [本文引用:1]
[10]	Carpenter J, Clifford P. Improved particle filter for nonlinear problems[J]. IEEE Proc of Radar, Sonar and Navigation, 1999, 146(1): 2-7. [本文引用:1]
[11]	毛晓楠. 基于粒子滤波的图像分割算法研究[D]. 上海: 上海交通大学模式识别与图像处理研究所, 2008. Mao Xiao-nan. Research on image segmentation algorithm based on particle filter[D]. Shanghai: Institute of Image Processing and Pattern Recognition, Shanghai Jiao Tong University, 2008. [本文引用:1]
[12]	李昱辰. 基于粒子滤波的视频目标跟踪方法研究[D]. 兰州: 兰州理工大学电气工程与信息工程学院, 2013. Li Yu-chen. Research of video target tracking methods based on particle filter[D]. Lanzhou: College of Electrical and Information Engineering, Lanzhou University of Technology, 2013. [本文引用:1]
[13]	于金霞, 汤永利, 刘文静. 粒子滤波自适应机制研究综述[J]. 计算机应用研究, 2010, 27(2): 417-422. Yu Jin-xia, Tang Yong-li, Liu Wen-jing. A survey on adaptive mechanism of particle filter[J]. Applications Research of Computers, 2010, 27(2): 417-422. [本文引用:1]
[14]	Mikami D, Otsuka K, Yamato J. Memory-based particle filter for tracking objects with large variation in pose and appearance[C]//Proceedings of the European Conference on Computer Vision, Crete, Greece, 2010: 215-228. [本文引用:1]
[15]	Tang Y, Bai X, Yang X, et al. Skeletonization with particle filters[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2010, 24(4): 619-634. [本文引用:1]
[16]	张苗辉, 刘先省. 基于无味粒子滤波的动态场景下高机动目标跟踪[J]. 光电子激光, 2010, 30(6): 924-929. Zhang Miao-hui, Liu Xian-xing. Maneuverable target tracking in dynamic scene based on unscented particle filter[J]. Journal of Optoelectronics Laser, 2010, 30(6): 924-929. [本文引用:1]

2010

0.0

. 2010, 35(11):1925-1929

Technologies of monitoring and communication in the coal mine

煤矿安全生产监控与通信技术

Sun Ji-ping.

孙继平

从煤矿安全监控、煤矿井下人员位置监测、煤炭产量远程监测、全矿井移动通信、无人值守远程监控技术及系统等几个方面介绍了煤矿监控与通信技术现状。在此基础上展望了煤矿监控与通信技术的研究方向，即矿用物联网技术与系统，煤矿一体化通信技术与系统，无人工作面遥控和煤岩分界识别技术与系统，煤矿井下人员精确定位技术与系统，基于煤矿安全监控系统的瓦斯、火灾、冲击地压等煤矿重大灾害预警技术与系统，基于3D GIS的煤矿安全生产管理信息系统，煤矿井下生命探测技术与装备，本质安全无线通信与光纤通信技术，传感器无盲区布置方法，煤矿井下救灾机器人等。

... 煤矿智能视频监控系统能够改变以往人工监控的模式,自动分析理解视频画面中的内容,发现监控场景中存在的异常行为、可疑目标和潜在危险,迅速发出实时警报,从而指导启动相应的联动控制措施^[1,2,3] ...

2007

0.0

. 2007, 36(5):597-602

Recognizing empty trainsin coalmine surveillance images

矿井监控图像中空列车的识别

Sun Ji-ping , Chen Wei , Wang Fu-zeng

孙继平, 陈伟, 王福增

2011

0.0

. 2011, :-

Research on object detection and tracking algorithm and its application in coal mine

视频目标检测与跟踪算法及其在煤矿中应用的研究[D]

Li Dan.

厉丹

远程视频监控系统是矿井安全生产系统的一个重要的组成部分,针对煤矿井下作业远离地面、环境恶劣、地形复杂的情况,地面监控人员可以对井下实时监控,直观监视现场的生产情况,及时发现安全隐患,防患于未然,同时能为事故后期分析提供第一手资料。目前井下视频监控主要依靠人工监控,日夜值守,工作量极其繁重,且由于固有的生理特点,可能疲倦和懈怠,难以达到实时、准确、主动的要求。现阶段热点研究的智能视觉监控技术可以最大限度减少人工干预,减轻了工人负担,提高监控效率。然而受井下环境背景复杂多变、噪声大、粉尘多、照度不均、分辨率低等因素的影响,易导致目标分辨性不强。若将现有检测算法直接应用于井下,效果并不理想。本文主要针对煤矿复杂环境通过计算机视觉方法来自动分析摄像机拍摄的序列视频图像,实现场景中目标定位、识别及跟踪,为进一步分析判断目标行为打下基础。本文主要工作如下: 提出适合煤矿井下特殊环境的危险区域目标检测算法,解决多摄像机不同视角目标匹配问题。算法基于SIFT多尺度变换,将改进的K-d树用于特征点匹配搜索,提高了搜索效率,同时结合样本主成分分析实现特征向量降维,利用RANSAC和L-M非线性优化算法估计优化参数。算法对煤矿井下模糊、低照度、遮挡、高噪声和尺度变化等情况均有良好的鲁棒性,解决现有算法计算复杂,匹配时间长,复杂环境匹配精度低的问题。提出根据互功率谱相位相关冲激函数能量高效检测重叠区域实现图像快速粗匹配,对乱序帧制定排序方法,并结合多频带提升小波,利用数据相关性融合规则进行多分辨率融合实现无缝平滑拼接。实验表明,本文算法提高了匹配效率,拼接效果平滑自然,抗噪声、光照等环境变化,适合煤矿环境。针对Snake模型寻优过程中抗噪能力差、不能向凹处收敛等问题,对Snake模型进行改进,使其自动分配蛇点,具有拓扑自适应性,并将粗收敛结果作为粒子群算法的初始轮廓,同时提出自适应惯性权重非线性调整的学习策略,提高收敛精度。针对粒子群优化过程中易丧失群体多样性和易收敛于局部极值的问题,利用遗传算法中育种和变异思想改进,淘汰适应度低的粒子,增加相邻粒子间约束。单峰、多峰函数的测试和图像仿真结果证实了改进算法的有效性。结合基于GAC和C-V模型的变分水平集算法有效实现煤块分割,较好解决了大煤块堵仓问题。针对Camshift算法仅依靠颜色模型,直接将其应用于照度不均、噪声大的井下环境极易丢失目标的问题,提出融合多特征的自适应模板更新算法。新算法在Camshift算法基础上,融合纹理、边缘等特征,通过建立特征模板,各特征根据贡献度合理分配权重,在环境变化时自适应更新模板。通过划分子区域,提取各区域量化后特征直方图信息作为子区域特征,建立遮挡时目标跟踪模型。在不同环境中进行算法比较,实验证实改进算法可以实现特征间互补不足,有较强抗干扰能力。

2014

0.0

. 2014, 39(1):198-204

Clearing research on fog and dust images in coalmine intelligent video surveillance

煤矿智能视频监控中雾尘图像的清晰化研究

Zhang Xie-hua , Zhang Shen , Fang Shuai

张谢华, 张申, 方帅

... 本文针对煤矿井下智能视频监控系统这一特定的应用场合,考虑光照较暗、井下粉尘大、探照强光干扰多造成的模糊和噪声现象^[4,5],在低信噪比条件下进行井下目标的实时检测和跟踪,提出了一种基于多状态空间及关键区域采样粒子滤波的井下目标自动检测方法 ...

2015

0.0

. 2015, 35(5):1435-1438 DOI:doi:10.11772/j.issn.1001-9081.2015.05.1435

Enhancement algorithm for fog and dust images in coal mine based on dark channel prior theory and bilateral adaptive filter

基于暗原色理论和自适应双边滤波的煤矿尘雾图像增强算法

Du Ming-ben , Chen Li-chao , Pan Li-hu.

杜明本, 陈立潮, 潘理虎

Concerning the problem that videos images captured from coal mines filled with coal dust and mist are often with quality problems such as lots of noise, low resolution and blur. To solve this problem, an enhancement algorithm for fog and dust images in coal mine based on dark channel prior theory and bilateral adaptive filter was proposed. On the basis of dark channel prior, the softmatting process was replaced with the adaptive bilateral filtering to obtain fine transmittance map. Then according to the special circumstances of coal mines, the global atmosphere light and the rough transmittance map were got from new perspective and image denoising was realized on the basis of the image degradation model. The experiment results show that the image processing time for a resolution of 1024×576 is 1.9 s. Compared with He algorithm (HE K, SUN J, TANG X. Single image haze removal using dark channel prior. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011,33(12):1-13.), the efficiency increased 5 times.Compared with other algorithms such as histogram equalization method, the proposed algorithm is effective to enhance the image detail. In this way, images can be more suitable for human vision as a whole.

针对煤矿井下存在大量煤尘、水雾导致获取的视频图像伴有大量的噪声、分辨率低、模糊的问题,提出了一种基于暗原色理论和自适应双边滤波的煤矿尘雾图像增强算法.基于暗原色先验理论,采用自适应双边滤波代替softmatting过程来求取精细透射率图,并根据煤矿井下特殊环境,从新的角度求取全球大气光值、粗略透射率图,并根据图像退化模型实现图像的去噪.实验结果表明,对于分辨率为1024×576的图像处理时间为1.9s,与He算法(HE K, SUN J, TANG X. Single image haze removal using dark channel prior. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011,33(12):1-13.)相比,运行效率提高了5倍.与直方图均衡法等算法相比,所提算法有效增强了图像细节、边缘,整体上更加适合人类视觉和视频监控的要求.

2014

0.0

... 1 模糊目标检测系统模型粒子滤波(Particle filter,PF)算法也称为序列化蒙特卡洛方法(Sequential Monte-Carlo methods,SMCM),该方法的基本思想是通过随机粒子抽样传播概率密度,用一组带有权值的随机采样粒子表示系统状态的后验概率密度(Posterior probability density function,PDF),并利用该粒子集以样本均值方法计算当前系统状态的估计值^[6],不但避免了对目标状态矩阵的积分运算,而且为解决非线性、非高斯动态系统中的目标检测及跟踪问题提供了一种简便、有效的方法^[7,8] ...

1996

0.0

1993

0.0

2014

0.0

. 2014, :-

Research of vehicle tracking methods based on particle filter and incremental learning

基于粒子滤波与增量学习的车辆跟踪方法硏究[D]

Wu Gang.

吴刚

现代交通运输智能化涉及车辆自身的智能化与道路交通智能监控。智能车辆采用视觉系统针对周围车辆进行跟踪,有助于对潜在接近或危险行驶的车辆进行合理规避；道路交通智能监控环境中,针对车道上的行驶车辆进行目标跟踪,有助于提取交通流速度、车道的占有率与瞬时车速等交通信息量。符合目标状态非线性、噪声分布非高斯的粒子滤波算法由于既适用静止视觉平台,同时又适合移动视觉平台,成为目前跟踪算法的一个较优选择。在图像受随机噪声扰动、车辆受遮挡、车速变化等场景下,传统车辆跟踪算法的成功率与处理速度均难以完全匹配智能车视觉系统的要求；对于道路交通智能监控,基于图像的车辆跟踪算法也存在不能完全适应光照强度变化、阴影、雨雪雾天等问题。作为传统预测跟踪方法,粒子滤波算法自身缺乏智能性应对复杂场景车辆跟踪的有效解决手段。针对上述复杂车辆跟踪场景,论文侧重在融合粒子滤波与增量学习方面,研究进一步提高粒子滤波跟踪算法稳定性、实时性与可靠性的解决方法。本论文主要研究复杂场景中的运动车辆跟踪方法,研究成果与取得的创新点体现在以下主要方面：(1)为解决传统粒子滤波序列重要性重采样(Sequential Importance Resampling, SIR)算法因引进简化的建议分布,引起粒子权值近似计算从而导致跟踪稳定性欠佳的问题,利用相邻帧间信息的强关联性,使用前帧先验与系统状态预测信息共同采样粒子以校正预测粒子点信息,提出一种引入前帧加权采样的粒子滤波跟踪算法。基于标准视频Car11的车辆跟踪实验表明：对道路灯光扰动下车速发生变化的车辆进行跟踪,所提算法提高粒子滤波SIR算法跟踪的稳定性。为进一步降低重采样误差并提高粒子滤波的采样效率,既通过引入当前粒子集权值的残差信息来构建合理的累积分布函数,又通过分层的手段来获取有序的随机数集合,在多项式重采样的基础上提出残差信息分层重采样。针对标准测试视频,对比嵌入4种重采样的粒子滤波SIR跟踪算法的实验数据表明：在跟踪误差与收敛粒子数方面,嵌入残差信息分层重采样的粒子滤波算法性能为最优。(2)针对车辆运动方向持续变化、目标车辆距离远近变化、光照强度变化等场景下,稳定且实时性地跟踪车辆的难点问题,基于自相关矩阵增量主成分分析(Incremental Principal Component Analysis,IPCA)增量学习与粒子滤波算法的基础上提出一种基于表观模型的车辆跟踪方法,不需预先训练车辆图像、且不需假定目标车辆的子空间均值固定,从跟踪初始利用自相关矩阵与特征值分解构建车辆的子空间图像,通过IPCA增量学习后的子空间均值、特征向量基共同参与似然概率密度的计算,提高粒子滤波算法粒子权值计算的精度。在粒子数选取300个、每5帧进行一次IPCA增量学习的情况下,基于Car4等3组标准视频的跟踪实验表明：对比P.Hall-IPCA粒子滤波与D.Ross-IPCA粒子滤波方法,所提AM-IPCA粒子滤波方法将车辆跟踪成功率分别由82.7%-92.3%、92.1%-95.2%提升至95.1%-96.4%。(3)长序列图像跟踪场景中,车辆跟踪过程经常受跟踪区域形变、光照强度变化等现场强噪声干扰,为解决跟踪算法的跟踪窗口易产生形变与漂移的难点问题,利用群空间中仿射群组受扰动后的形不变性,将系统状态变量映射到李群空间进行处理,同时采用IPCA增量学习并更新目标特征子空间。在利用粒子滤波算法采样粒子时,通过引入观测量以提高粒子权值计算的准确性。所提跟踪器可以在现场强噪声的扰动下长时段稳健地跟踪车辆,跟踪窗口自适应地调整大小与角度以不断适应车辆姿态和距离远近的持续变化。基于Dtneu_schnee等4个标准视频的跟踪实验表明：对比同类别跟踪器VTD、IVT和Kwon2010,所提自适应跟踪器将跟踪成功率分别由91.3%～95.7%、82.9%-94.2%、94.6%-96.7%提升N96.1%～97.7%。(4)针对车辆在经历遮挡、运动状态变化及雨雪噪声扰动下的跟踪难点问题,并非一味地采用预测跟踪算法对车辆进行长时段跟踪,结合粒子滤波、Online Boosting在线分类器及其增量学习、样本相似度与半监督学习提出SSOBI粒子滤波跟踪算法,利用当前时刻观测数据、相邻帧与系统状态预测信息共同增强粒子滤波的粒子采样合理性,避免粒子滤波的建议分布过于依赖系统状态预测而处于一定的局部最优范围之内；粒子滤波合理的建议分布则有效地缩小在线增量学习样本的检测范围,加快Online Boosting的学习并有效解决增量学习过程中存在的自学习问题。针对Dtneu_winter等测试视频的跟踪实验表明：车辆面临部分遮挡时,对比Online Boosting、半监督Online Boosting算法,SSOBI粒子滤波算法将跟踪成功率分别由66.5%～73.3%、76.4%～82.5%提升至88.5%-90.0%。

... 视频目标检测的任务在粒子滤波框架下转化为在视频序列中使用观测数据推理出检测目标的空间状态的问题,即在时变动态系统中估计状态空间参数,状态推理框架中包括两种模型^[9,10]:①动态模型,描述目标状态在时间维上的演变过程 ...

1999

0.0

2008

0.0

. 2008, :-

Research on image segmentation algorithm based on particle filter

基于粒子滤波的图像分割算法研究[D]

Mao Xiao-nan.

毛晓楠

图像分割(Image Segmentation)是将图像分成若干具有特定意义的区域并将它们提取出来的图像处理技术。图像分割是图像理解和图像识别的前提,是图像理解与识别的初级阶段。图像分割的大致发展过程为早期的基于灰度和梯度的经典分割技术,如阈值法、边缘和区域技术;八十年代的活动轮廓模型技术,如参数活动轮廓模型和几何活动轮廓模型;以及近年来的结合形状等先验知识的分割方法,如活动形状模型和活动表面模型。图像分割技术的发展过程呈现了这样的趋势,也即所使用的先验信息越来越多,所具有的智能化程度越来越高,分割能力也将越来越强。本文从状态估计的角度考察图像分割问题,将它视为非高斯、非线性条件下的状态估计问题。粒子滤波是处理非高斯、非线性条件下状态估计问题的有力理论工具,它已经广泛用于解决目标跟踪、信号处理等领域中时间序列范畴的问题。已有一些学者尝试着将这一理论工具用于非时间序列范畴的领域,例如Patrick等借助目标跟踪算法的思路解决边缘跟踪问题。红外目标提取和彩色图像目标轮廓提取是图像分割中的两个常见问题。本文着重研究了在粒子滤波理论框架下解决这两个问题。基于粒子滤波的红外目标提取算法针对实际应用出现的低信噪比红外图像目标提取问题。基于经典的阈值分割思想,本文将目标提取问题看作阈值的估计问题,并在粒子滤波理论框架中对阈值进行估计。本文建立了基于像素值以及灰度-方差加权信息熵的阈值状态空间;借鉴了粒子群优化的思想,构建了PSO状态转移方程;综合考虑红外目标的视觉特征,提出了基于平均灰度、梯度信息、像素点聚合程度、像素点数量、目标区域灰度方差加权信息熵的评价函数,并以此构建观测模型。与2D-Otsu和二维最大熵法等经典的二维阈值方法相比,本文综合考虑了目标的视觉信息,算法的稳健性得到提高;与基于粒子群优化和2D-Otsu方法的红外目标提取算法相比,算法的迭代次数明显减少。基于粒子滤波的目标轮廓提取算法主要应用于彩色图像的目标轮廓提取。本文将彩色图像目标轮廓提取问题视为非线性、非高斯条件下的状态估计问题,并尝试以粒子滤波这一理论工具解决之。本文研究目标轮廓提取问题的出发点可以简单的概括成“化曲为直”,即目标的连续轮廓可以看做由N段长度为dl的单元线段构成的序列。基于“化曲为止”的思想和状态估计的数学方法,轮廓提取问题就可以简化为逐次计算这N个线段的问题,进而又可以转化为对斜率和截距这两个直线特征参数的估计。本文首先通过梯度算子和基于彩色空间聚类的方法给出目标轮廓的预测C p,用以引导轮廓提取;之后建立基于直线斜率k和截距b的二维状态空间(粒子采样空间),并在此基础上对每个单位线段dl进行估计;建立基于PSO状态转移模型的粒子状态转移方程;建立基于Snake能量函数的观测模型;最后以粒子集的加权平均值作为状态输出。实验证明了算法的有效性。本文主要研究和解决了如下问题: (1)状态空间的建立。建立状态空间是应用粒子滤波理论框架解决实际问题的基础,这直接关系到Monte Carlo方法的采样效率。在红外目标提取问题中,建立了基于像素值和灰度-方差信息熵的阈值空间;在目标轮廓提取问题中,在“化曲为直”思想的基础上,建立了基于单元线段参数的二维状态空间。 (2)建议性分布的建立。在目标轮廓提取问题中,采用梯度算子和基于颜色空间聚类的方法给出预测轮廓以引导目标轮廓的生成。 (3)状态转移模型的建立。在红外目标提取问题和目标轮廓提取问题中,均采用了基于粒子群优化思想的PSO状态转移模型。该模型可以使粒子不断地向已知的最优解靠近,以达到改善粒子的分布,加快算法收敛的目的。 (4)观测模型的建立。观测模型的设计是应用粒子滤波理论框架解决实际问题的关键。在红外目标提取问题中,本文提出了基于平均灰度、梯度信息、像素点聚合程度、像素点数量、目标区域灰度方差加权信息熵的评价函数,并以此构建观测模型,较传统的二维最大类间差(2D-Otsu)准则、二维最大熵准则(2D-KSW)而言,该观测模型更好的利用了红外目标的视觉特征。在目标轮廓提取问题中,采用了Snake模型中的能量函数来建立观测模型。

... 在贝叶斯最优估计框架下,许多非线性问题的求解都要求计算高维积分,基于随机采样运算的蒙特卡罗方法可以模拟贝叶斯估计求解问题^[11,12] ...

2013

0.0

... 在贝叶斯最优估计框架下,许多非线性问题的求解都要求计算高维积分,基于随机采样运算的蒙特卡罗方法可以模拟贝叶斯估计求解问题^[11,12] ...

2010

0.0

. 2010, 27(2):417-422 DOI:doi:10.3969/j.issn.1001-3695.2010.02.005

A survey on adaptive mechanism of particle filter

粒子滤波自适应机制研究综述

Yu Jin-xia , Tang Yong-li , Liu Wen-jing.

于金霞, 汤永利, 刘文静

针对粒子滤波固有的缺陷,结合移动机器人领域的研究应用成果,分别从样本数目自适应、重采样自适应、建议分布自适应、运动/似然模型自适应以及与其他方法的集成等几个方面对粒子滤波自适应机制当前研究的关键技术进行了归纳总结,并且对该研究领域需要解决的研究难点进行了总结,对进一步研究的方向进行了展望. Abstract： Aimed at the inherent deficiency in particle filter and combined with the up-to-date research and application in the mobile robot field,this paper summarized some key technologies in current study from the adaptive mechanism of sample size respectively,the resampling strategy,proposal distribution,motion/likelihood model and the integration with other methods.At the same time,concluded the main challenges that needed to be solved in this field and also presented some future trends about the technology of these difficulties.

... 1 粒子采样设系统状态 xk,n服从一阶Markov过程, xk,n与系统观测值 zk,n相互独立^[13] ...

2010

0.0

... 3 状态估计输出当迭代到第k步时,k时刻的系统状态后验分布p(x_k |z_k)能够由加权粒子集 {xki,ωki}近似表示^[14],视频帧系统目标状态 xk的最小均方误差估计为: ...

2010

0.0

... 这个问题会增加大量的计算时间,但是对系统状态的估计不起任何作用,降低了算法性能^[15] ...

2010

0.0

. 2010, 30(6):924-929

Maneuverable target tracking in dynamic scene based on unscented particle filter

基于无味粒子滤波的动态场景下高机动目标跟踪

Zhang Miao-hui , Liu Xian-xing.

张苗辉, 刘先省

... 解决权值退化的常用方法是重要性重采样方法^[16],它是对随机采样粒子和表示其相应权值的概率密度函数进行重新采样,将权值较小的粒子删除,增加权值较大的粒子,重新得到一组新的粒子样本 ...