考虑桥面铺装作用的简支梁桥横向分布系数计算

引用本文

魏志刚, 刘寒冰, 时成林, 宫亚峰. 考虑桥面铺装作用的简支梁桥横向分布系数计算[J].吉林大学学报（工学版）, 2018,48(1): 105-112
WEI Zhi-gang, LIU Han-bing, SHI Cheng-lin, GONG Ya-feng. Calculation of transverse distribution coefficient of simply supported beam bridge with effect of bridge deck pavement[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 105-112 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161304
Permissions

考虑桥面铺装作用的简支梁桥横向分布系数计算

魏志刚^1,², 刘寒冰¹, 时成林^1,³, 宫亚峰¹

1.吉林大学交通学院,长春 130022

2.吉林省高等级公路建设局,长春 130033

3.吉林省交通科学研究所科研开发中心,长春 130012

通讯作者：宫亚峰(1977-),男,副教授,博士. 研究方向:路桥健康监测与灾害治理. E-mail:gongyf@jlu.edu.cn

作者简介:魏志刚(1977-),男,高级工程师,博士研究生. 研究方向:桥梁检测与加固.E-mail:wzg770718@163.com

基金:国家自然科学基金项目(51478203, 51378236); 中央高校基本科研业务费专项资金项目

摘要

为了准确计算考虑桥面铺装参与受力的简支梁桥横向分布系数,基于刚接梁法的基本原理,考虑了混凝土桥面铺装与主梁间存在的剪切滑移效应,采用结构力学中的基本方法提出了一种考虑桥面铺装的简支梁桥荷载横向分布系数计算方法,本文称之为修正刚接梁法。采用本文方法计算了一座实际简支T梁桥的横向分布系数,并以此计算了车辆荷载作用下各主梁的挠度和铺装层应变等静力响应,并与试验结果进行了对比分析。结果表明,计算出的静力响应与实测静力响应吻合度很高,充分说明了本文方法的准确性和可靠性。

关键词: 桥梁工程; 桥面铺装; 横向分布系数; 剪切滑移; 修正刚接梁法

中图分类号:TU311.1,U441 文献标志码:A 文章编号:1671-5497(2018)01-0105-08

Calculation of transverse distribution coefficient of simply supported beam bridge with effect of bridge deck pavement

WEI Zhi-gang^1,², LIU Han-bing¹, SHI Cheng-lin^1,³, GONG Ya-feng¹

1.College of Transportation,Jilin University,Changchun 130022, China

2.Jilin Provincial High Class Highway Construction Bureau,Changchun 130033,China

3.Scientific Research and Development Center,Jilin Provincial Transport Scientific Research Institute,Changchun 130012,China

Abstract

In order to accurately calculate the transverse distribution coefficient of simply supported beam bridge considering the effect of bridge deck pavement, based on the idea of rigid-jointed beam, a new method for calculating the transverse distribution coefficient was proposed, using the methods in structural mechanics. This method is referred as the modified rigid-jointed beam method, in which the effect of shear slip between concrete bridge deck pavement and the main girder was considered. The transverse distribution coefficient of an actual simply supported T-shaped beam bridge was calculated using the proposed method, the deflection of each main girder and the static response such as the strain of the bridge deck pavement under vehicle load were obtained and compared with experimental results. It is shown that the calculated static response is in good agreement with the measured one, which verifies the accuracy and reliability of proposed modified rigid-jointed beam method.

Keyword: bridge engineering; bridge deck pavement; transverse distribution coefficient; shear slip; modified rigid-jointed beam method

Show Figures

0 引言

对于工程技术人员来说, 在对简支梁桥进行受力分析时, 多采用横向分布系数的概念将空间受力体系转化为单梁模型。针对不同的桥梁结构形式, 在进行受力体系转化时引进的假定是不同的, 因此便产生了多种横向分布系数计算方法。目前, 较为常用的方法有铰接板法^[1]、偏心压力法、杠杆原理法、刚接梁法^[2]及比拟正交异性板法^[3]等。其实每种横向分布系数计算方法都具有一定的适用条件^[4], 这是由进行受力体系转换时引进的假定决定的, 针对这一点国内外学者开展了大量的研究工作。有关研究资料表明^{[5, 6]}, 当简支梁桥的宽跨比大于0.5时, 比拟正交异性板法和刚接梁法比较适用。刚接梁法不但可以考虑主梁刚度和间距的差异, 与比拟正交异性板法相比, 还具有计算过程简便、易实现程序化等优点^[7], 因此该方法得到了广泛应用。

混凝土桥面铺装不但能够参与主梁的受力, 而且还是决定荷载横向分配的一个因素。目前常用的横向分布系数计算方法中都没有考虑桥面铺装的作用, 这是因为这种做法对桥梁设计来说是安全的, 但对于桥梁检测则是不安全的^[8]。当人们意识到此问题后, 便在考虑桥面铺装的荷载横向分布方面开展了研究工作^[9]。目前的研究工作主要有两方面的缺陷:一方面是简单地认为桥面铺装与主梁完全结合, 其实这两者是存在剪切滑移效应的, 这便导致研究成果可能会存在一定的不准确性; 另一方面是多采用有限元方法建立考虑桥面铺装的桥梁结构模型, 依据模型进行一些数值分析以揭示桥面铺装对横向分布系数存在影响这一事实, 而没有给出有效的横向分布系数计算方法。

本文针对主梁间距较大的简支梁桥, 将横梁和桥面板等效成板, 各主梁保持不变, 同时考虑桥面铺装的作用, 根据刚接梁法的基本思想, 给出了一种便于广大工程技术人员掌握的、考虑桥面铺装参与受力的横向分布计算方法。

1 刚接梁法的基本原理

在刚接梁方法中, 由n+1片主梁构成的简支梁桥对应的力法方程为:

C· g+δ _p=0(1)

式中:g=[g₁g₂ … g_n m₁m₂ … m_n]^T为赘余力矩阵; δ _p=[δ ₁_p δ ₂_p … δ _np 0 0 … 0]^T为外荷载作用下的相对位移; C为力法原理中由常变位组成的系数矩阵, 可以采用分块矩阵的形式表示:

C= $\begin{matrix} [\begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix}] \end{matrix}$ (2)

式中:由赘余剪力g_i产生的竖向相对位移C₁₁为:

C₁₁= $\begin{matrix} [\begin{matrix} δ_{1, 1} & δ_{1, 2} & \dots & δ_{1, n} \\ δ_{2, 1} & δ_{2, 2} & \dots & δ_{2, n} \\ ⋮ & ⋮ & ⋮ \\ δ_{n, 1} & δ_{n, 2} & \dots & δ_{n, n} \end{matrix}] \end{matrix}$

由赘余剪力g_i产生的竖向相对转角C₂₁为:

C₂₁= $\begin{matrix} [\begin{matrix} δ_{(n + 1), 1} & δ_{(n + 1), 2} & \dots & δ_{(n + 1), n} \\ δ_{(n + 2), 1} & δ_{(n + 2), 2} & \dots & δ_{(n + 2), n} \\ ⋮ & ⋮ & ⋮ \\ δ_{(2 n), 1} & δ_{(2 n), 2} & \dots & δ_{(2 n), n} \end{matrix}] \end{matrix}$

由赘余力矩m_i产生的相对位移C₁₂为:

C₁₂= $\begin{matrix} [\begin{matrix} δ_{1, (n + 1)} & δ_{1, (n + 2)} & \dots & δ_{1, (2 n)} \\ δ_{2, (n + 1)} & δ_{2, (n + 2)} & \dots & δ_{2, (2 n)} \\ ⋮ & ⋮ & ⋮ \\ δ_{n, (n + 1)} & δ_{n, (n + 2)} & \dots & δ_{n, (2 n)} \end{matrix}] \end{matrix}$

由赘余力矩m_i产生的相对转角C₂₂为:

C₂₂= $\begin{matrix} [\begin{matrix} δ_{(n + 1), (n + 1)} & δ_{(n + 1), (n + 2)} & \dots & δ_{(n + 1), (2 n)} \\ δ_{(n + 2), (n + 1)} & δ_{(n + 2), (n + 2)} & \dots & δ_{(n + 2), (2 n)} \\ ⋮ & ⋮ & ⋮ \\ δ_{(2 n), (n + 1)} & δ_{(2 n), (n + 2)} & \dots & δ_{(2 n), (2 n)} \end{matrix}] \end{matrix}$

2 修正刚接梁法计算公式的推导

2.1 基本假定

混凝土桥面铺装与主梁是分两次浇筑完成的, 在界面处既不是完全结合, 也不是完全脱离, 而是在界面处存在剪切滑移效应。根据界面处力的传递情况和刚接梁法的基本原理, 给出如下基本假定:①桥面铺装和主梁各自符合平截面假定; ②桥面水泥混凝土铺装层与主梁交界面处存在滑移, 交界面的水平剪力与相对滑移差成正比; ③忽略桥面水泥混凝土铺装与主梁顶板交界面处的竖向掀起现象, 认为交界面没有竖向掀起, 外荷载作用下桥面水泥混凝土铺装层和主梁的竖向位移、转角以及曲率相同; ④主梁与主梁之间的桥面板考虑为刚性连接, 二者在翼板交界处既能够传递剪力又能够传递弯矩; ⑤将汽车车列比拟为半波正弦荷载, 各梁所分配的荷载与挠度成正比。

修正刚接梁法的关键在于在考虑桥面铺装与主梁存在剪切滑移的情况下, 如何形成常变位系数矩阵C。在得到了常变位系数矩阵和载变位δ _p后, 利用式(1)便可以计算出各主梁的横向分布系数。

2.2 竖向赘余力作用下的位移求解

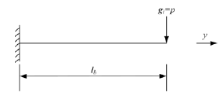
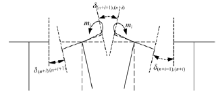
当翼缘板端部作用有竖向赘余力g_i时(见图1(a)), 可将其移至主梁的中心位置, 形成如图1(b)所示的一个中心荷载和偏心力矩共同作用的受力形式。由此可知, 翼缘板端部的竖向位移由主梁的竖向挠度v、主梁扭转产生的翼缘板端部竖向位移bφ /2和g_i引起的翼缘板端部下挠f三部分组成。

	Figure Option View Download New Window
	图1 主梁横断面受力模式Fig.1 Force of main girder cross section

2.2.1 主梁跨中截面竖向挠度v求解

当半波正弦荷载作用于主梁中心位置时, 考虑桥面铺装参与受力的主梁平衡方程为(g_i以方向向上为正):

M_p(x)= $\begin{matrix} \frac{p l^{2}}{π^{2}} \end{matrix}$ sin $\begin{matrix} (\frac{πx}{l}) \end{matrix}$ (3)

式中:p为半波正弦荷载的峰值; M_p(x)为p作用下的弯矩; l为主梁计算跨径; x为截面位置。

由文献[10]可知, 主梁形心处的轴向位移为:

$\begin{matrix} u_{b 0}^{'} \end{matrix}$ (x)=a₁cosh(Rx)+a₂sinh(Rx)+ $\begin{matrix} \frac{z_{d} p l^{2}}{β B_{0} π^{2}} \end{matrix}$ sin $\begin{matrix} (\frac{πx}{l}) \end{matrix}$ (4)

式中:a₁、a₂为待定系数; z_d为桥面铺装形成至主梁形心的距离; B₀为主梁与铺装抗弯刚度之和; β 含义同文献[10]。

竖向半波正弦荷载作用下, 梁端的边界条件为:

$\begin{matrix} \{\begin{matrix} x = 0, N_{b} (0) = E_{b} A_{b} u_{b 0}^{'} (0) = 0 \\ x = l, N_{b} (l) = E_{b} A_{b} u_{b 0}^{'} (l) = 0 \end{matrix} \end{matrix}$ (5)

将式(5)代入式(4), 可得:a₁=0, a₂=0。因此有:

$\begin{matrix} u_{b 0}^{'} \end{matrix}$ (x)=- $\begin{matrix} \frac{z_{d} p l^{2}}{β B_{0} π^{2}} \end{matrix}$ sin $\begin{matrix} (\frac{πx}{l}) \end{matrix}$ (6)

同时有:

v^″(x)=- $\begin{matrix} \frac{1}{z_{d}} \end{matrix} \begin{matrix} [\frac{E_{b} A_{b}}{k} u_{b 0}^{‴} (x) + (1 + \frac{E_{b} A_{b}}{E_{p} A_{p}}) u_{b 0}^{'} (x)] \end{matrix}$ (7)

式中:E_b、E_p分别为主梁和铺装层的弹性横量; A_b、A_p分别为主梁和铺装的横断面面积; k为主梁与铺装这间的剪切滑移刚度。

综合式(6)(7)可得:

v(x)= $\begin{matrix} \frac{p l^{2}}{β B_{0} π^{2}} \end{matrix} \begin{matrix} [\frac{E_{b} A_{b}}{k} + (1 + \frac{E_{b} A_{b}}{E_{p} A_{p}}) \frac{l^{2}}{π^{2}}] \end{matrix}$ × sin $\begin{matrix} (\frac{πx}{l}) \end{matrix}$ +a₃x+a₄ (8)

根据简支梁的边界条件可得主梁跨中挠度为:

v= $\begin{matrix} \frac{p l^{2}}{β B_{0} π^{2}} \end{matrix} \begin{matrix} [\frac{E_{b} A_{b}}{k} + (1 + \frac{E_{b} A_{b}}{E_{p} A_{p}}) \frac{l^{2}}{π^{2}}] \end{matrix}$ (9)

2.2.2 跨中截面扭转角φ 的求解

在偏心力矩作用下, 主梁产生扭转变形, 其扭转平衡方程为:

GI_T $\begin{matrix} \frac{d^{2} φ}{d x^{2}} \end{matrix}$ =-m_T(x)=- $\begin{matrix} \frac{b}{2} \end{matrix}$ psin $\begin{matrix} \frac{πx}{l} \end{matrix}$ (10)

式中:G为剪切模量; I_T为抗扭惯性矩; m_T(x)为x截面的据矩。

由式(10)进行两次积分, 可得:

GI_Tφ (x)= $\begin{matrix} \frac{pb l^{2}}{2 π^{2}} \end{matrix}$ sin $\begin{matrix} \frac{πx}{l} \end{matrix}$ +a₅x+a₆ (11)

式中:a₅、a₆为待定系数。

由边界条件可得:

φ (x)= $\begin{matrix} \frac{pb l^{2}}{2 π^{2} G I_{T}} \end{matrix}$ sin $\begin{matrix} \frac{πx}{l} \end{matrix}$ (12)

因此, 主梁跨中截面的转角为:

φ = $\begin{matrix} \frac{pb l^{2}}{2 π^{2} G I_{T}} \end{matrix}$ (13)

2.2.3 翼缘板下挠f的求解

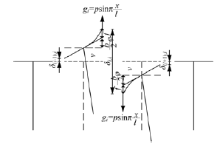
基于弹性力学基本原理, 悬臂板端部作用有分布荷载时, 翼缘板某一断面的位移可以取单位板宽按悬臂梁求解, 如图2所示。悬臂梁的横断面为桥面铺装层与桥面板层组成的组合截面, 采用h_x表示计及横梁等代刚度的桥面板厚度, h_p表示水泥混凝土桥面铺装的厚度。

	Figure Option View Download New Window
	图2 悬臂梁受力图示Fig.2 Diagram of force of cantilever beam

根据力的平衡关系, 图2所示悬臂组合梁在y位置处的内外力平衡方程为:

$\begin{matrix} \{\begin{matrix} M_{1 p} (y) + M_{1 b} (y) - N_{1 b} (y) z_{1 d} = p (l_{b} - y) \\ N_{1 b} (y) + N_{1 p} (y) = 0 \end{matrix} \end{matrix}$ (14)

式中:l_b为悬臂组合梁的长度; M₁_p、M₁_b、N₁_p、N₁_b、z₁_d如图3所示。

还有:

q(x)=k[u₁_p₀(y)-u₁_b₀(y)- $\begin{matrix} v_{1}^{'} \end{matrix}$ (y)z₁_d]=

E_pA₁_p $\begin{matrix} u_{1 p 0}^{″} \end{matrix}$ (y) (15)

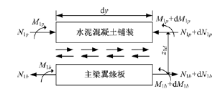
式中:u₁_p₀(y)为水泥混凝土铺装沿y方向的轴向位移; u₁_b₀(y)为主梁翼缘板沿y方向的轴向位移; $\begin{matrix} v_{1}^{'} \end{matrix}$ (y)为悬臂组合梁的转角; z₁_d=(h_p+h_x)/2, 为桥面水泥混凝土桥面铺装与主梁翼缘板形心轴间距。

由弹性力学基本原理可知, 悬臂组合梁的微元体dy受力如图3所示。

	Figure Option View Download New Window
	图3 悬臂组合梁微元体受力图示Fig.3 Diagram of force of micro unit of cantilever composite beam

由式(14)(15)并根据图3所示的微元体受力分析, 可得:

$\begin{matrix} \{\begin{matrix} E_{b} A_{1 b} u_{1 b 0}^{'} (y) + E_{p} A_{1 p} u_{1 p 0}^{'} (y) = 0 \\ p (l_{b} - y) = B_{01} v_{1}^{″} (y) - E_{b} A_{1 b} u_{1 b 0}^{'} (y) z_{1 d} \end{matrix} \end{matrix}$ (16)

式中:A₁_b为主梁翼缘板横断面面积; A₁_p为桥面铺装层横断面面积; B₀₁=( $\begin{matrix} h_{p}^{3} \end{matrix}$ + $\begin{matrix} h_{x}^{3} \end{matrix}$ )/12。

联立式(15)(16)可得:

α ₁ $\begin{matrix} u_{b 0}^{‴} \end{matrix}$ (y)-β ₁ $\begin{matrix} u_{b 0}^{'} \end{matrix}$ (y)=β ₁γ ₁(l_b-y)(17)

式中:α ₁= $\begin{matrix} \frac{E_{b} A_{1 b}}{k_{1}} \end{matrix}$ ; β ₁= $\begin{matrix} (1 + \frac{E_{b} A_{1 b}}{E_{p} A_{1 p}} + \frac{E_{b} A_{1 b} z_{1 d}^{2}}{B_{01}}) \end{matrix}$ ; γ ₁= $\begin{matrix} \frac{p z_{1 d}}{β_{1} B_{01}} \end{matrix}$ ; k₁为铺装和翼缘板之间的滑移刚度。

式(17)为三阶常微分方程, 可求解其显式表达如下:

$\begin{matrix} u_{b 0}^{'} \end{matrix}$ (y)=a₇cosh(R₁y)+a₈sinh(R₁y)+

γ ₁(l_b-y) (18)

式中:R₁= $\begin{matrix} \sqrt[]{β_{1} / α_{1}} \end{matrix}$ ; a₇、a₈为待定系数。

联立式(15)~式(18), 可得:

$\begin{matrix} \{\begin{matrix} u_{b 0}^{″} (y) = a_{7} Rsinh (R_{1} y) + a_{8} Rcosh (R_{1} y) + γ_{1} \\ u_{b 0} (y) = a_{7} \frac{\sinh (R_{1} y)}{R_{1}} + a_{8} \frac{\cosh (R_{1} y)}{R_{1}} - \\ γ_{1} (l_{b} y - \frac{y^{2}}{2}) + a_{9} \\ v_{1}^{″} (y) = a_{7} α_{B} \cosh (R_{1} y) + a_{8} α_{B} \sinh (R_{1} y) - \\ \frac{E_{b} A_{1 b} z_{1 d} γ_{1} - p}{B_{01}} (l_{b} - y) \\ v_{1}^{'} (y) = a_{7} \frac{α_{B}}{R_{1}} \sinh (R_{1} y) + a_{8} \frac{α_{B}}{R_{1}} \cosh (R_{1} y) - \\ (α_{B} γ_{1} - \frac{p}{B_{01}}) (l_{b} y - \frac{y^{2}}{2}) + a_{10} \\ v_{1} (y) = a_{7} \frac{α_{B}}{R_{1}^{2}} \cosh (R_{1} y) + a_{8} \frac{α_{B}}{R_{1}^{2}} \sinh (R_{1} y) - \\ (α_{B} γ_{1} - \frac{p}{B_{01}}) (\frac{l_{b}}{2} y^{2} - \frac{y^{3}}{6}) + a_{10} x + a_{11} \\ u_{1 p 0}^{'} (y) = - a_{7} α_{1 p} \cosh (R_{1} y) - a_{8} α_{1 p} \sinh (R_{1} y) + \\ γ_{1} α_{1 p} (l_{b} - y) \\ u_{1 p 0} (y) = - a_{7} \frac{α_{1 p}}{R} \sinh (R_{1} y) - a_{8} \frac{α_{1 p}}{R} \cosh (R_{1} y) + \\ γ_{1} α_{1 p} (l_{b} y - \frac{y^{2}}{2}) + a_{12} \end{matrix} \end{matrix}$ (19)

式中:α ₁_p= $\begin{matrix} \frac{E_{b} A_{1 b}}{E_{p} A_{1 p}} \end{matrix}$ ; α _B= $\begin{matrix} \frac{E_{b} A_{1 b} z_{1 d}}{B_{01}} \end{matrix}$ ; a₉~a₁₂为待定系数。

悬臂梁的边界条件为N_b(l_b)=0, u_p₀(0)=0, u_b₀(0)=0, v(0)=0, v^'(0)=0, $\begin{matrix} u_{b 0}^{″} \end{matrix}$ (0)=0, 依据边界条件, 由式(19)可得:

f(l_b)= $\begin{matrix} \frac{(p - E_{b} A_{1 b} z_{d} γ_{1}) l_{b}^{3}}{3 B_{01}} \end{matrix}$ + $\begin{matrix} \frac{E_{b} A_{1 b} z_{d} γ_{1} l_{b}}{B_{01} R_{1}^{2}} \end{matrix}$ -

$\begin{matrix} \frac{E_{b} A_{1 b} z_{1 d} γ_{1} \tanh (R_{1} l_{b})}{B_{01} R_{1}^{3}} \end{matrix}$ (20)

2.2.4 g_i作用下常变位的求解

竖向赘余力g_i作用下的位移如图4所示。

	Figure Option View Download New Window
	图4 竖向赘余力产生的位移图示Fig.4 Diagram of displacement generated by vertical redundant

δ _i_,_i为刚接梁法常变位系数矩阵中的主系数, 由主梁跨中挠度、主梁扭转和主梁翼缘板端部下挠3部分组成:

δ _i_,_i=2 $\begin{matrix} [\frac{l^{2}}{B_{0} π^{2}} (\frac{l^{2}}{π^{2}} + \frac{E_{b} A_{b} l^{2}}{E_{p} A_{p} π^{2}} + \frac{E_{b} A_{b}}{k}) + \frac{b^{2} l^{2}}{4 π^{2} G I_{T}} + \end{matrix} \begin{matrix} \frac{(1 - E_{b} A_{1 b} z_{d} γ_{1}) l_{b}^{3}}{3 B_{01}} \end{matrix}$ + $\begin{matrix} \frac{E_{b} A_{1 b} z_{d} γ_{1} l_{b}}{B_{01} R_{1}^{2}} \end{matrix}$ - $\begin{matrix} \frac{E_{b} A_{1 b} z_{1 d} γ_{1} \tanh (R_{1} l_{b})}{B_{01} R_{1}^{3}}] \end{matrix}$ (21)

δ ₍_i-_1),_i、δ _i_{, (}_i-₁₎为刚接梁法常变位系数矩阵中的副系数, 包括主梁跨中挠度和主梁跨中截面扭转产生的翼缘板端部位移。

δ ₍_i+_1),_i=δ ₍_i-_1),_i=- $\begin{matrix} \frac{l^{2}}{B_{0} π^{2}} \end{matrix} \begin{matrix} [(1 + \frac{E_{b} A_{b}}{E_{p} A_{p}}) \frac{l^{2}}{π^{2}} + \end{matrix} \begin{matrix} \frac{E_{b} A_{b}}{k}] \end{matrix}$ + $\begin{matrix} \frac{b^{2} l^{2}}{4 π^{2} G I_{T}} \end{matrix}$ (22)

δ ₍_n+i-_1),_i、δ ₍_n+i+_1),_i为单位半波正弦荷载偏心产生的翼缘板端部转角相对位移, 二者大小相等, 方向相反。

$\begin{matrix} \{\begin{matrix} δ_{(n + i - 1), i} = - \frac{b l^{2}}{2 π^{2} G I_{T}} \\ δ_{(n + i + 1), i} = \frac{b l^{2}}{2 π^{2} G I_{T}} \end{matrix} \end{matrix}$ (23)

2.3 赘余力矩m_i作用下的常变位求解

赘余力矩m_i作用下翼缘板端部的位移模式如图5所示。在m_i作用下, 基本结构在跨中截面将产生扭转, 导致在翼缘板端部形成竖向位移, 该竖向位移由扭转产生的翼缘板端部竖向位移bφ /2和翼缘板端部挠度f两部分组成。

	Figure Option View Download New Window
	图5 赘余力矩作用下翼缘板端部位移Fig.5 Displacement of end of flange slab under superfluous moment

2.3.1 跨中截面扭转角φ 的求解

在扭矩作用下, 主梁产生扭转变形, 此时对应的扭转平衡方程为:

GI_T $\begin{matrix} \frac{d^{2} φ}{d x^{2}} \end{matrix}$ =-m_i(x)=-m_Tsin $\begin{matrix} \frac{πx}{l} \end{matrix}$ (24)

由式(24)积分可得:

GI_Tφ (x)= $\begin{matrix} \frac{m_{T} l^{2}}{π^{2}} \end{matrix}$ sin $\begin{matrix} \frac{πx}{l} \end{matrix}$ +a₁₃x+a₁₄ (25)

式中:a₁₃、a₁₄为待定系数。

根据主梁扭转边界条件, 可解得主梁跨中截面的扭转角为:

φ = $\begin{matrix} \frac{m_{T} l^{2}}{π^{2} G I_{T}} \end{matrix}$ (26)

2.3.2 跨中截面翼缘板端部转角的求解

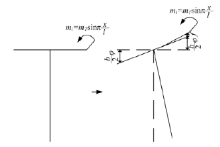
由于m_i属于分布力矩, 在m_i作用下基本结构翼缘板的受力可取单位板宽, 按悬臂梁分析, 悬臂梁端部作用有大小为m_T的力矩, 如图6所示。

	Figure Option View Download New Window
	图6 半波正弦力矩荷载作用下的悬臂梁Fig.6 Cantilever beam under half wave sine moment

由图6可知, 根据力的平衡关系可得:

$\begin{matrix} \{\begin{matrix} - m_{i} = M_{1 p} (x) + M_{1 b} (x) - N_{1 b} (x) z_{1 d} \\ N_{1 b} (x) + N_{1 p} (x) = 0 \end{matrix} \end{matrix}$ (27)

由式(27)可知:

$\begin{matrix} \{\begin{matrix} E_{b} A_{1 b} u_{1 b 0}^{'} (y) + E_{p} A_{1 p} u_{1 p 0}^{'} (y) = 0 \\ m_{i} = - B_{01} v_{1}^{″} (y) + E_{b} A_{1 b} u_{1 b 0}^{'} (y) z_{1 d} \end{matrix} \end{matrix}$ (28)

由式(15)、式(28)可得:

$\begin{matrix} \{\begin{matrix} u_{1 p 0}^{'} (y) = - \frac{E_{b} A_{1 b}}{E_{p} A_{1 p}} u_{1 b 0}^{'} (y) \\ - \frac{E_{b} A_{b}}{k} u_{1 b 0}^{‴} (y) = u_{1 p 0}^{'} (y) - u_{1 b 0}^{'} (y) - z_{1 d} v^{″} (y) \\ v_{1}^{″} (y) = - \frac{m_{i}}{B_{01}} + \frac{E_{b} A_{1 b} z_{1 d}}{B_{01}} u_{1 b 0}^{'} (y) \end{matrix} \end{matrix}$ (29)

由式(29)可解得:

$\begin{matrix} \{\begin{matrix} u_{1 b 0} (x) = a_{15} \frac{1}{R_{1}} \sinh (R_{1} y) + a_{16} \frac{1}{R_{1}} \cosh (R_{1} y) - \\ γ_{2} x + a_{17} \\ u_{1 p 0}^{'} (x) = - a_{15} k_{α} \cosh (R_{1} y) - a_{16} k_{α} \sinh (R_{1} y) + γ_{2} k_{α} \\ u_{1 p 0} (x) = - a_{15} \frac{k_{α}}{R_{1}} \sinh (R_{1} y) - a_{16} \frac{k_{α}}{R_{1}} \cosh (R_{1} y) \\ + γ_{2} k_{α} y + a_{18} \\ v^{″} (x) = \frac{m_{i}}{B_{01}} + a_{15} k_{β} \cosh (R_{1} y) + a_{16} k_{β} \sinh (R_{1} y) + γ_{2} k_{β} \\ v^{'} (x) = a_{15} \frac{k_{β}}{R_{1}} \sinh (R_{1} y) + a_{16} \frac{k_{β}}{R_{1}} \cosh (R_{1} y) + \\ (\frac{m_{i}}{B_{01}} - k_{β}) y + a_{19} \\ v (x) = a_{15} \frac{k_{β}}{R_{1}^{2}} \cosh (R_{1} y) + a_{16} \frac{k_{β}}{R_{1}^{2}} \sinh (R_{1} y) + \\ (\frac{m_{i}}{B_{01}} - k_{β}) \frac{y^{2}}{2} + a_{19} y + a_{20} \end{matrix} \end{matrix}$ (30)

式中:k_α= $\begin{matrix} \frac{E_{b} A_{1 b}}{E_{p} A_{1 p}} \end{matrix}$ ; k_β= $\begin{matrix} \frac{E_{b} A_{1 b} z_{1 d}}{B_{01}} \end{matrix}$ ; a₁₅~a₂₀为待定系数。

由边界条件可求得主梁翼缘板端部的转角为:

φ (l_b)=v^'(l_b)= $\begin{matrix} \frac{k_{β} γ_{2} \sinh (R_{1} l_{b})}{R_{1}^{2} \cosh (R_{1} l_{b})} \end{matrix}$ +

$\begin{matrix} \frac{1 - E_{b} A_{1 b} z_{1 d} γ_{2} l_{b}}{B_{01}} \end{matrix}$ (31)

2.3.3 m_i作用下常变位的求解

图7给出了单位半波正弦力矩作用下主梁跨中截面的位移图示。

	Figure Option View Download New Window
	图7 赘余力矩产生的转角图示Fig.7 Diagram of angle generated by superfluous moment

赘余力矩对应的刚接梁法常变位系数矩阵中的主系包括主梁产生的相对扭转角和赘余力矩引起的翼缘板端部相对扭转角两部分。

δ ₍_n+i_{), (}_n+i₎=2 $\begin{matrix} [\frac{l^{2}}{π^{2} G I_{T}} + \frac{γ_{2} E_{b} A_{1 b} z_{1 d} \sin (R_{1} l_{b})}{B_{01} R_{1} \cos (R_{1} l_{b})} \end{matrix}$ + $\begin{matrix} \frac{1 - E_{b} A_{1 b} z_{1 d} γ_{2}}{B_{01}} \end{matrix}$ l_b (32)

赘余力矩产生的转角副系数计算如下:

δ ₍_n+i-_{1), (}_n+i₎=δ ₍_n+i_{), (}_n+i+₁₎=- $\begin{matrix} \frac{l^{2}}{π^{2} G I_{T}} \end{matrix}$ (33)

赘余力矩产生的位移副系数是赘余力矩导致主梁扭转形成的相对竖向位移, 具体表达式如下:

$\begin{matrix} \{\begin{matrix} δ_{(i - 1), (n + i)} = \frac{b l^{2}}{2 π^{2} G I_{T}} \\ δ_{(i + 1), (n + i)} = - \frac{b l^{2}}{2 π^{2} G I_{T}} \end{matrix} \end{matrix}$ (34)

2.4 改进刚接梁法的横向分布影响线求解

2.4.1 力法方程中载变位的求解

式(1)给出的力法方程中, 载变位是由单位半波正弦荷载作用于主梁轴线时对应的主梁跨中截面的挠度, 因此由式(9)可求得得半波正弦荷载作用在第j号梁时对应的载变位δ _p。

当i=j-1时, 有:

δ ₍_j-₁₎_p= $\begin{matrix} \frac{p l^{2}}{B_{0} π^{2}} \end{matrix} \begin{matrix} [\frac{E_{b} A_{b}}{k} + (1 + \frac{E_{b} A_{b}}{E_{p} A_{p}}) \frac{l^{2}}{π^{2}}] \end{matrix}$ (35)

当i=j时, 有:

δ _jp=- $\begin{matrix} \frac{p l^{2}}{B_{0} π^{2}} \end{matrix} \begin{matrix} [\frac{E_{b} A_{b}}{k} + (1 + \frac{E_{b} A_{b}}{E_{p} A_{p}}) \frac{l^{2}}{π^{2}}] \end{matrix}$ (36)

式中:δ ₍_j-₁₎_p、δ _jp为p作用下第j-1和j个接缝处的相对变形。

当i> j或i< j-1时, 有:

δ _jp=0(37)

2.4.2 改进刚接梁法横向分布影响线竖标值的求解

已知力法方程中的常变位和载变位, 由式(2)便可以求得当单位半波正弦荷载作用于j号梁时基本结构对应的赘余铰接力g_ij。进而求得改进刚接梁法对应的横向分布影响线竖标值η _ij, 具体的求解公式如下:

η _ij= $\begin{matrix} \{\begin{matrix} g_{(i - 1) j} - g_{ij}, i \neq j \\ 1 + g_{(i - 1) j} - g_{ij}, i = j \end{matrix} \end{matrix}$ (38)

式中:η _ij为荷载作用于j号主梁对应的i号主梁梁位处的横向影响线竖标值。

3 实体工程验证

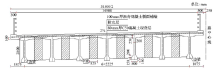
把本文方法应用到了一座30 m跨径简支T梁桥检测的实际工程中, 该桥共由7片主梁组成, 桥宽14.5 m, 横断面如图8所示。首先对该桥进行了静力加载, 加载现场如图9所示, 并测试了各主梁跨中截面的挠度, 各主梁跨中截面铺装层底面应变以及边梁铺装层底面应变。接着采用本文方法计算了在考虑桥面铺装作用下各主梁的横向分布影响线, 据此得到了各主梁分担到的试验荷载, 进而计算了与实验相同的项目。最后把计算结果和实测结果进行了对比分析。

	Figure Option View Download New Window
	图8 桥梁上部结构跨中横断面图示Fig.8 Diagram of cross section of bridge superstructure in mid-span

	Figure Option View Download New Window
	图9 加载现场图示Fig.9 Diagram of field test

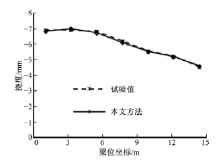
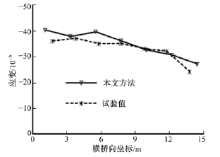
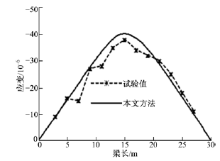
由图10~图12可知, 各主梁跨中截面的挠度, 各主梁跨中截面铺装层底面应变以及边梁铺装层底面应变这3个参数的计算值与实测值吻合较好, 充分说明了本文方法的可靠性和有效性。

	Figure Option View Download New Window
	图10 各主梁跨中截面挠度Fig.10 Deflection in mid-span cross section of each main girder

	Figure Option View Download New Window
	图11 各主梁跨中截面铺装层地面应变Fig.11 Ground strain of pavement in mid-span cross section of each main girder

	Figure Option View Download New Window
	图12 边梁铺装层地面应变分布Fig.12 Ground strain distribution of edge beam pavement

4 结束语

基于刚接梁法的基本原理, 考虑混凝土桥面铺装与主梁间存在剪切滑移效应, 采用结构力学中的基本方法形成了一种考虑桥面铺装的简支梁桥荷载横向分布系数计算方法, 并把该方法应用到了一座30 m跨径简支T梁桥检测的实际工程中。实际工程应用表明, 各主梁跨中截面的挠度、各主梁跨中截面铺装层底面应变以及边梁铺装层底面应变这3个参数的计算值与实测值吻合较好, 充分说明了本文方法的可靠性和有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	成琛, 沈成武, 许亮. 用铰接板(梁)法计算有损伤桥梁的横向分布系数[J]. 武汉理工大学学报: 交通科学与工程版, 2004, 28(2): 229-231. Cheng Chen, Shen Cheng-wu, Xu Liang. The hinged-jointed plate method for calculating transverse load distribution on a damaged bridge[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2004, 28(2): 229-231. [本文引用:1]
[2]	桂水荣, 陈水生. T形梁的组合板-梁桥荷载横向分布系数研究[J]. 华东交通大学学报, 2009, 26(3): 1-5. Gui Shui-rong, Chen Shui-sheng. A research of live-load distribution coefficient for T-type flitch beam bridge[J]. Journal of East China Jiaotong University, 2009, 26(3): 1-5. [本文引用:1]
[3]	陈强, 孟阳君, 周先雁. 大宽跨比桥梁横向分布系数的快速计算方法[J]. 重庆交通大学学报: 自然科学版, 2011, 30(6): 1287-1289. Chen Qiang, Meng Yang-jun, Zhou Xian-yan. Rapid computation method of transverse distribution coefficients about bridges with big wide-span ratio[J]. Journal of Chongqing Jiaotong University (Natural Sciences), 2011, 30(6): 1287-1289. [本文引用:1]
[4]	Barr P J, Eberhard M O, Stanton J F. Lived-load distribution factors in prestressed concrete girder bridges[J]. Journal of Bridge Engineering, 2001, 6(5): 298-306. [本文引用:1]
[5]	Hughes E A. Lived-load distribution factors for prestressed concrete, spread box-girder bridge[J]. Journal of Bridge Engineering, 2006, 11(5): 573-578. [本文引用:1]
[6]	Yousif Z, Hindi R. AASHTO-LRFD live load distribution for beam-and -slab brides: limitations and applicability[J]. Journal of Bridge Engineering, 2007, 12(6): 765-773. [本文引用:1]
[7]	聂建国, 张晓光, 樊健生, 等. 钢-混凝土组合梁加宽混凝土梁桥的横向分布系数[J]. 清华大学学报: 自然科学版, 2010, 50(6): 805-809. Nie Jian-guo, Zhang Xiao-guang, Fan Jian-sheng, et al. Transverse distribution coefficient of concrete bridges widened with steel-concrete composite beams[J]. Journal of Tsinghua University (Science and Technology), 2010, 50(6): 805-809. [本文引用:1]
[8]	时成林. 季冻区中小跨径桥梁桥面铺装及考虑其影响的主梁受力特性研究[D]. 长春: 吉林大学交通学院, 2016. Shi Cheng-lin. Research on bridge deck pavement and mechanical characteristics of girder considering the influencing of deck pavement for medium-small span bridges in seasonal frozen area [D]. Changchun: College of Transportation, Jilin University, 2016. [本文引用:1]
[9]	曾智. 混凝土桥梁铺装层受力分析和横向分布系数计算[D]. 武汉: 武汉理工大学土木工程与建筑学院, 2004. Zeng Zhi. Force analysis and transverse distribution coefficient calculation of concrete bridge deck pavement [D]. Wuhan: School of Civil Engineering and Architecture, Wuhan University of Technology, 2004. [本文引用:1]
[10]	刘寒冰, 时成林, 谭国金. 考虑剪切滑移效应的叠合梁有限元解[J]. 吉林大学学报: 工学版, 2016, 46(3): 792-797. Liu Han-bing, Shi Cheng-lin, Tan Guo-jin. Finite element solution of composite beam with effect of shear slip[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(3): 792-797. [本文引用:1]

2004

0.0

. 2004, 28(2):229-231 DOI:doi:10.3963/j.issn.2095-3844.2004.02.021

The hinged-jointed plate method for calculating transverse load distribution on a damaged bridge

用铰接板(梁)法计算有损伤桥梁的横向分布系数

Cheng Chen , Shen Cheng-wu , Xu Liang.

成琛, 沈成武, 许亮

给出分析有损伤桥梁荷载横向分布系数计算的铰接板(梁)法模型和一般方程,讨论了不同损伤位置和损伤程度对横向分布系数的影响,并针对某病桥的实测数据,运用遗传算法对损伤位置与程度进行识别,其模型计算的横向分布系数与实际情况吻合,表明此模型和方法是可行的.

... 目前,较为常用的方法有铰接板法^[1]、偏心压力法、杠杆原理法、刚接梁法^[2]及比拟正交异性板法^[3]等 ...

2009

0.0

. 2009, 26(3):1-5 DOI:doi:10.3969/j.issn.1005-0523.2009.03.001

A research of live-load distribution coefficient for T-type flitch beam bridge

T形梁的组合板-梁桥荷载横向分布系数研究

Gui Shui-rong , Chen Shui-sheng.

桂水荣, 陈水生

根据现浇桥面板的T形组合简支板-梁桥结构特点,采用平面模型(偏心压力法、刚接板(梁)法)和空间模型(有限单元法)计算该组合简支板-梁桥荷载横向分布系数.运用通用结构分析软件ANSYS将该组合板-梁桥离散成空间有限元.分析该桥荷载横向分布系数变化规律.并将刚接板(梁)法及ANASYS解法计算结果与实测结果进行对比研究.研究结果表明:偏心压力法不适于计算该类组合板梁桥荷载横向分布系数;刚接板(梁)法全桥各截面采用同一横向分布系数并不精确,而ANSYS计算结果能与实测值较好的吻合;同时提出了适合该类桥型的横向分布系数计算方法,并建议了更加准确的计算方法.

... 目前,较为常用的方法有铰接板法^[1]、偏心压力法、杠杆原理法、刚接梁法^[2]及比拟正交异性板法^[3]等 ...

2011

0.0

. 2011, 30(6):1287-1289 DOI:doi:10.3969/j.issn.1674-0696.2011.06.06

Rapid computation method of transverse distribution coefficients about bridges with big wide-span ratio

大宽跨比桥梁横向分布系数的快速计算方法

Chen Qiang , Meng Yang-jun , Zhou Xian-yan.

陈强, 孟阳君, 周先雁

基于正交异性板法原理,从理论上推导了荷载作用下的横向分布表达式,并采用分段函数对其进行拟合;不仅提高了计算效率,而且精度大大提高;同时推导的横向分布表达式还可用于模块化编程,为工程软件分析提供基础。

... 目前,较为常用的方法有铰接板法^[1]、偏心压力法、杠杆原理法、刚接梁法^[2]及比拟正交异性板法^[3]等 ...

2001

0.0

... 其实每种横向分布系数计算方法都具有一定的适用条件^[4],这是由进行受力体系转换时引进的假定决定的,针对这一点国内外学者开展了大量的研究工作 ...

2006

0.0

... 有关研究资料表明^[5,6],当简支梁桥的宽跨比大于0 ...

2007

0.0

... 有关研究资料表明^[5,6],当简支梁桥的宽跨比大于0 ...

2010

0.0

. 2010, 50(6):805-809

Transverse distribution coefficient of concrete bridges widened with steel-concrete composite beams

钢-混凝土组合梁加宽混凝土梁桥的横向分布系数

Nie Jian-guo , Zhang Xiao-guang , Fan Jian-sheng

聂建国, 张晓光, 樊健生

摘　要：在用钢-混凝土组合梁加宽混凝土梁桥时,计算了加宽后的混凝土梁桥横向分布系数。在刚接梁法基础上,考虑了组合梁与原桥主梁刚度、间距差异,建立了修正的刚接梁计算方法。研究了刚性横梁法在新加宽后的桥梁中的适用范围,考虑了组合梁和新横梁的条件。用MSC.Marc有限元软件模型、修正的刚接梁法、刚性横梁法进行计算。用这几种方法对加宽后的混凝土梁桥横向分布系数计算结果,均与桥梁实测结果吻合良好。

... 刚接梁法不但可以考虑主梁刚度和间距的差异,与比拟正交异性板法相比,还具有计算过程简便、易实现程序化等优点^[7],因此该方法得到了广泛应用 ...

2016

0.0

. 2016, :-

Research on bridge deck pavement and mechanical characteristics of girder considering the influencing of deck pavement for medium-small span bridges in seasonal frozen area

季冻区中小跨径桥梁桥面铺装及考虑其影响的主梁受力特性研究

Shi Cheng-lin.

时成林

对于中小跨径桥梁而言,桥面铺装的主要功能是保护主梁,即避免车轮荷载直接磨耗行车道板和防止水分渗入到桥面板,同时不可避免要参与主梁受力,为主梁分担荷载。由于桥面铺装结构形式的复杂性和使用条件的恶劣性,导致桥面铺装出现病害的现象屡屡发生,并且破坏形式还具有明显的地域特点。我国中小跨径混凝土桥梁量大面广,即使是简单的维护也需投入大量的资金,因此开展中小跨径桥梁的桥面铺装研究十分必要。其研究意义主要体现在两个方面:一方面是在恶劣的使用条件下,如何避免或减少桥面铺装本身的病害;另一方面是中小跨径桥梁的梁高不大,刚度较小,桥面铺装参与主梁受力的程度较高,如何把握其影响,准确的计算主梁受力特性对于桥梁检测等工作意义非凡。在避免或减少桥面铺装本身的病害方面,人们围绕桥面铺装构造形式、材料及受力状态分析开展了大量的研究工作。由于水泥混凝土铺装层与桥面板的粘结性能要强于沥青混凝土铺装层与水泥混凝土铺装层的粘结性能,人们普遍关注的是沥青混凝土铺装层与水泥混凝土铺装层的粘结特性,常常忽视水泥混凝土铺装层与桥面板之间的粘结特性。有关研究资料表明,二者结合面会出现滑动,在车辆、温度等荷载的反复作用下甚至发生剪切破坏。在考虑桥面铺装的主梁受力特性分析方面,目前的研究成果比较少。其实水泥混凝土铺装层与桥面板之间的接触既不是完全结合、也不是完全脱离,水泥混凝土铺装层与桥面板之间的接触状态直接影响了桥面铺装参与主梁受力的程度。对于中小跨径混凝土桥梁的检测而言,如果不能在进行主梁受力状态分析时,定量的把握层间接触状态,准确的考虑桥面铺装的影响,会导致测试到的主梁力学特性与理论计算值之间存在较大差异,从而使得桥梁状态评估结果不够准确。通过文献检索还未发现以层间接触状态的定量表达为基础,考虑桥面铺装影响的主梁受力特性计算方法。为了解决上述问题,本文结合吉林省重大科技攻关项目“季冻区桥梁绿色生态桥面铺装材料研究及产品开发”和交通运输部西部交通建设科技项目“季冻区公路应对极端气候的快速维护与安全保障技术研究”,开展了季冻区中小跨径混凝土桥梁桥面铺装构造形式及考虑桥面铺装的主梁受力特性方法研究。以改善层间粘结能力为出发点,提出了一种适用于季冻区中小跨径混凝土桥梁的桥面铺装构造形式。该构造最大特点是在原有钢筋连接的基础上,在桥面板上设置凹槽,以改善水泥混凝土铺装层和桥面板之间的粘结能力。采用自行设计的试验装置,测试了不同条件下防水粘结层的粘结性能,并分析了其温度敏感性。设计了22组不同配筋率和不同凹槽间距、凹槽尺寸等参数情况下水泥混凝土铺装层与桥面板层间剪切试件,测试了各组试件的剪切性能,并分析了各参数对剪切性能的影响。提出采用抗剪刚度来定量表征层间接触状态,并给出了水泥混凝土铺装层与桥面板的层间抗剪刚度及剪切强度经验公式。为了能够准确计算考虑桥面铺装的主梁受力状态,采用抗剪刚度来体现层间接触状态,形成了考虑桥面铺装的单梁静力特性分析方法;对刚接梁法进行改进,建立了能够考虑桥面铺装影响的桥梁横向分布系数计算方法。并将上述方法应用到一座30m跨径简支T梁桥的实际工程中。车辆作用会导致桥梁动力特性的变异,桥面铺装同样会影响桥梁的动力特性。如何分析出车辆和桥面铺装共同影响下的主梁动力特性对于桥梁检测或监测来说意义重大。以水泥混凝土铺装层与桥面板之间层间抗剪刚度为基础,考虑桥面铺装对主梁刚度的贡献,形成了车辆作用下考虑桥面铺装的主梁动力特性计算方法。

... 目前常用的横向分布系数计算方法中都没有考虑桥面铺装的作用,这是因为这种做法对桥梁设计来说是安全的,但对于桥梁检测则是不安全的^[8] ...

2004

0.0

. 2004, :- DOI:doi:10.7666/d.y719761

Force analysis and transverse distribution coefficient calculation of concrete bridge deck pavement

混凝土桥梁铺装层受力分析和横向分布系数计算

Zeng Zhi.

曾智

随着公路等级的提高,桥梁涵洞等公路构造物所站比重越来越大,而高等级公路对路面质量要求较高,良好的路面结构设计和高标准的施工设备及严格的施工技术已使路面质量达到了相应的指标,如我国近期所修筑的高速公路,行车舒适性大大的提高.相反,桥面平整度差和沥青混凝土剥落问题日益严重,对高速行驶车辆的安全性构成了一定程度的威胁.近年来全国各地不少桥面建成不久,桥面铺装就出现了严重的破损、开裂、坑槽、拥包等病害,给交通造成很大的不便,严重时还容易造成交通事故.这些问题引起了人们对桥面铺装的重视.本文就桥面铺装出现的各种病害情况进行...

... 当人们意识到此问题后,便在考虑桥面铺装的荷载横向分布方面开展了研究工作^[9] ...

2016

0.0

. 2016, 46(3):792-797 DOI:doi:10.13229/j.cnki.jdxbgxb201603017

Finite element solution of composite beam with effect of shear slip

考虑剪切滑移效应的叠合梁有限元解

Liu Han-bing , Shi Cheng-lin , Tan Guo-jin.

刘寒冰, 时成林, 谭国金

为了准确计算叠合梁在荷载作用下的受力、位移,基于弹性力学基本思想和接触理论推导了考虑剪切滑移效应的叠合梁的有限元解.利用该有限元解计算了集中荷载作用下的叠合梁挠度和交界面剪切滑移,并与试验结果进行了对比分析,结果表明:有限元解与试验结果能够较好地吻合,彼此具有较强的相关性,验证了有限元解的准确性和可靠性,为分析叠合梁受力和变形提供了新的计算手段,具有较高的实际推广价值.