预应力RPC-NC叠合梁挠度试验及计算方法

引用本文

季文玉, 李旺旺, 过民龙, 王珏. 预应力RPC-NC叠合梁挠度试验及计算方法[J].吉林大学学报（工学版）, 2018,48(1): 129-136
JI Wen-yu, LI Wang-wang, GUO Min-long, WANG Jue. Experimentation and calculation methods of prestressed RPC-NC composite beam deflection[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 129-136 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161204
Permissions

预应力RPC-NC叠合梁挠度试验及计算方法

季文玉, 李旺旺, 过民龙, 王珏

北京交通大学土木建筑工程学院,北京 100044

通讯作者：李旺旺(1988-),男,博士研究生. 研究方向:桥梁结构理论与应用. E-mail:wangwangli@bjtu.edu.cn

作者简介:季文玉(1960-),男,教授,博士. 研究方向:桥梁结构理论与应用. E-mail:wyji@bjtu.edu.cn

基金:国家自然科学基金项目(51278040); 教育部中央高校基本科研业务费专项资金项目(2014YJS106)

摘要

为提高桥梁结构抵抗变形的能力,提出了预应力活性粉末混凝土(RPC)-普通混凝土(NC)叠合梁结构形式,并设计了10根预应力RPC-NC叠合模型梁和1根NC对照梁。试验研究了预应力度、RPC高度、NC等级等因素影响下叠合梁跨中挠度发展特性及计算方法。结果表明:叠合梁跨中挠度发展可分为开裂前弹性阶段、带裂缝工作阶段、普通钢筋屈服后迅速增长阶段3个阶段。预应力度越高,开裂前弹性段越长,开裂后屈服和强化阶段的刚度下降越快。根据试验值对铁路桥规和混凝土规范中的公式进行修正,修正后的计算结果与试验值吻合良好。

关键词: 道路工程; 活性粉末混凝土; 普通混凝土; 叠合梁; 等效刚度; 弯曲挠度

中图分类号:TU378.2 文献标志码:A 文章编号:1671-5497(2018)01-0129-08

Experimentation and calculation methods of prestressed RPC-NC composite beam deflection

JI Wen-yu, LI Wang-wang, GUO Min-long, WANG Jue

School of Civil Engineering,Beijing Jiaotong University,Beijing 100044,China

Abstract

To improve the anti-deformation capacity of bridge structure, prestressed Reactive Powder Concrete (RPC)-Normal Concrete (NC) composite beam is proposed and ten prestressed RPC-NC composite beams and one NC beam were designed. Experiments of the mid-span deflections of the composite beams are conducted and the calculation method of the reflection is proposed. The influence of the degree of prestress, height of RPC and concrete degree of NC are considered in the experiments. The results show that the developing process of the deflection of composite beam can be divided into three stages, the elastic stage before cracking, cracking stage, rapid increasing stage after the yield of reinforcement. The higher the degree of prestress is, the longer the elastic stage is before cracking of the mid-span load-deflection, and the faster the stiffness yield and strength phase fall. The formulas of code for design of concrete structure and code for design for design of reinforced and prestressed concrete structure of railway bridge and culvert are modified based on the testing results. The calculated results by the modified formulas are in good agreement with the testing results.

Keyword: road engineering; reactive powder concrete(RPC); normal concrete(NC); composite beam; equivalent stiffness; bending deflection

Show Figures

0 引言

活性粉末混凝土(Reactive powder concrete, RPC)作为一种新型高性能混凝土, 诞生于20世纪90年代的法国BOUYGUES实验室^[1], 自其出现便引起了土建行业科研人员的广泛关注和研究^{[2, 3, 4, 5, 6, 7]}。RPC材料拥有超高的力学性能和耐久性, 完全可以满足当前土建行业尤其是桥梁工程的发展需求^{[8, 9, 10]}, 目前在铁路、公路等重大项目中已有应用^{[11, 12]}, 但由于其制作工艺相对复杂, 不能满足当前现场施工要求, 大部分构件仍在工厂预制完成。另一方面, 由于其原材料未大规模生产, 造价相对昂贵, 导致其未被广泛应用。

RPC材料作为高性能材料使用在桥梁结构中, 在减小梁结构变形的同时能够大幅提高梁的抗裂能力和耐久性。本文将RPC材料应用于梁结构的下部, 充分发挥其高抗拉性能和耐久性, 梁结构的上部仍使用普通混凝土(Normal concrete, NC), 充分利用其高抗压性能。该结构形式在充分发挥二者材料性能优势的同时, 充分利用了二者同为水泥基材料的粘结性能^[13], 为保证叠合面粘结强度将原光圆箍筋替换为具有抗剪和抗拉拔能力的螺纹钢筋。该结构形式相对于纯RPC梁而言, 降低了结构造价, 有利于RPC材料的推广应用。

桥梁工程中梁结构的挠度一直是工程人员和科研人员关注的重点^{[14, 15]}。梁结构的挠度过大会带来行车安全、乘客舒适度及结构耐久性等方面的问题。梁结构短期挠度的精确计算也是桥梁设计人员所关心的重要问题。本文共制作11根模型梁, 9根试验梁用于研究预应力度和RPC高度对叠合梁挠度的影响, 2根对照梁用于对照NC等级不同和纯NC梁与RPC-NC叠合梁的差异。本文拟通过试验研究预应力RPC-NC叠合梁的变形性能及其短期挠度计算方法。

1 试验概况

1.1 模型梁设计

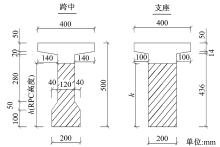
本文模型梁以铁路标准2101号跨度32 m T形梁为原型进行缩尺设计, 以相似理论、模型制作精度及现场试验条件为依据, 设计全长4.4 m, 试验跨度4.0 m, 剪跨段长度1.5 m, 中间纯弯段长度1.0 m。试验过程采用两点集中对称的同步分级加载方式, 两集中点的力由分配梁提供。模型试验梁均为后张法预应力施工, 施工过程中在梁的一端锚固振弦式压力传感器用于全程监测钢绞线张拉力。试验梁主要考虑预应力度、RPC高度、NC强度等级等因素对挠度的影响。各试验梁设计参数见表1, 预应力度 λ = σ _c/σ , 其中σ _c, σ 分别为由预加力和运营荷载引起的构件控制截面受拉边缘的应力。试验梁跨中和梁端截面具体尺寸见图1。

	Figure Option View Download New Window
	图1 模型梁截面尺寸Fig.1 Section size of model beam

表1 试验梁设计参数 Table 1 Design parameters of test beams

1.2 模型梁制作及材料性能试验

试验梁在中铁六局丰台桥梁厂内施工制作, 具体过程如下:①模型梁模板设计及制作; ②钢筋笼绑扎, 合模; ③RPC制备, 主要包括搅拌、振捣、蒸养等; ④RPC表面用清水浸润后浇筑NC; ⑤NC浇筑完成后, 进行3天室温养护后拆模, 浇水养护7天后进行自然养护; ⑥分级张拉钢绞线。

模型梁制作过程中, 预留每根梁的RPC与NC立方体试块、轴心抗压试块和抗折试块, 与模型梁进行同条件养护。每个直径的钢筋和钢绞线预留相应的材料性能试件。材料性能试验结果见表2和表3。

表2 RPC和NC实测材料性能 Table 2 Mechanics properties of RPC and NC

表3 钢筋实测力学性能 Table 3 Mechanics properties of steels and strands

1.3 加载与测量装置

试验加载与测量装置见图2。加载速度为4 kN/s, 每级持荷10 min。试验过程中主要采集试验梁跨中挠度, 梁顶荷载值, 跨中截面混凝土应力等数据。

	Figure Option View Download New Window
	图2 模型梁加载装置Fig.2 Test setup of model beams

2 试验结果与讨论

2.1叠合梁跨中挠度发展规律

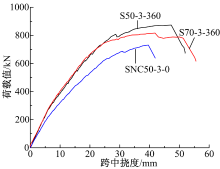
预应力RPC-NC叠合梁中RPC的弹性模量大于NC, 因此RPC的加入提高了截面刚度。图3给出了不同预应力等级下三根RPC-NC试验梁及一根纯NC对照梁的跨中荷载-挠度曲线。由图3可见叠合梁与NC梁跨中挠度-荷载曲线发展趋势相似, 可分为以下3个阶段:①开裂前弹性工作阶段, 由图3中圆圈标出, 该阶段跨中挠度呈线性增长; ②带裂缝工作阶段, 在出现第一转折点后试验梁进入带裂缝工作阶段, 挠度增长速度变大; ③钢筋屈服后迅速增长阶段, 在普通钢筋屈服后, 进入挠度迅速增长阶段, 试验梁荷载增加较少, 挠度迅速增长, 直至梁体破坏。

	Figure Option View Download New Window
	图3 RPC-NC叠合梁跨中挠度-荷载曲线Fig.3 Curves of load-displacement of RPC-NC composite beams

2.2 不同预应力度下叠合梁荷载-挠度曲线

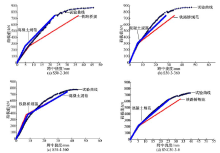
图4给出了不同预应力度下RPC-NC叠合梁跨中荷载-挠度曲线。开裂前弹性阶段, 预应力度越高开裂前弹性阶段越长, 挠度增长越缓慢; 带裂缝工作阶段, 预应力度越高刚度下降越快, 挠度增长越迅速, 最快进入屈服阶段; 屈服破坏阶段, 普通钢筋屈服后, 钢绞线仍具有一定承载能力, 曲线进入强化段, 预应力度越高钢绞线的作用越大强化段相对越长直至混凝土被压碎。

	Figure Option View Download New Window
	图4 不同预应力度下叠合梁荷载-挠度曲线Fig.4 Load-displacement curves of composite beams with different prestress ratio

2.3 不同RPC高度下叠合梁荷载-挠度曲线

图5给出了不同RPC高度下RPC-NC叠合梁跨中荷载-挠度曲线。开裂前弹性阶段基本一致; 带裂缝工作阶段, 竖向裂缝基本处于RPC部分, 曲线相差不大; 屈服破坏阶段, RPC高度越低, 裂缝越先进入NC部分, 普通钢筋屈服后迅速破坏, RPC越高对裂缝发展和挠度变形的约束作用越明显。

	Figure Option View Download New Window
	图5 不同RPC高度下叠合梁荷载-挠度曲线Fig.5 Load-displacement curves of composite beams with different RPC heights

2.4 对照组叠合梁荷载-挠度曲线

图6给出了对照试验梁的跨中荷载-挠度曲线, 其中S70-3-360梁用于对照不同NC等级对挠度的影响, SNC50-3-0梁用于对照纯NC梁与叠合梁的差别。由图6可见, 不同NC等级对荷载-挠度曲线前两个阶段影响很小, 而现实中的梁结构基本都处于前两个阶段, 可见NC等级的提高对荷载-挠度曲线影响不大。SNC50-3-0为纯NC梁, 由图6明显看出, RPC在加入叠合梁后可显著提高梁的刚度和开裂前的弹性工作段, 因此提高了梁在正常使用阶段抵抗变形和抗裂的能力。叠合梁的极限荷载和极限位移也明显高于纯NC梁。

	Figure Option View Download New Window
	图6 对照组叠合梁荷载-挠度曲线Fig.6 Load-displacement curves of composite beams of control group

3 短期刚度及挠度计算方法

通过以上叠合梁跨中荷载-挠度曲线的分析以及试验过程中叠合梁接触面未发生滑移可知, RPC-NC叠合梁可采用规范中的方法^{[16, 17]}计算短期挠度。由于现实中桥梁结构基本处于未开裂和带裂缝工作的前两个阶段, 因此本文仅计算叠合梁荷载-挠度曲线的前两个阶段。公式中的开裂荷载暂使用试验结果进行计算。

3.1 叠合梁跨中挠度计算

按照结构力学方法推导叠合梁跨中挠度计算公式, 结构受力形式见图7。结构的跨度l=4 m, 剪跨段l₁=1.5 m。根据梁变形的力平衡方程、变形协调方程以及物理关系建立近似微分方程, 再根据边界条件和连续条件求解得出模型梁跨中挠度公式如下:

ω ₂= $\begin{matrix} \frac{M (3 l^{2} + 4 l_{1}^{2})}{24 EI} \end{matrix}$ (1)

	Figure Option View Download New Window
	图7 结构受力示意图Fig.7 Schematic diagram of loading structure

3.2 叠合梁短期刚度及跨中挠度计算

RPC-NC叠合梁短期刚度采用有粘结预应力混凝土梁短期刚度的计算方法得出。本文分别取用《铁路桥涵钢筋混凝土和预应力混凝土结构设计规范》^[16]和《混凝土结构设计规范》^[17]中短期刚度计算方法。

铁路桥规范中开裂前短期刚度计算公式如下:

B=β _pβ ₁E_cI₀(2)

β _p= $\begin{matrix} \frac{1 + λ}{2} \end{matrix}$ (3)

β ₁= $\begin{matrix} \frac{λ - 0.5}{0.95 λ - 0.45} \end{matrix}$ (4)

铁路桥规范中带裂缝工作阶段短期刚度计算公式如下:

B=β ₁ $\begin{matrix} \frac{β_{p} β_{2} M}{β_{2} M_{f} + β_{p} (M - M_{f})} \end{matrix}$ E_cI₀(5)

β ₂=0.1+2n_pμ ≤ 0.5(6)

μ = $\begin{matrix} \frac{A_{p} + A_{s}}{b h_{0}} \end{matrix}$ (7)

式中:B为抗弯刚度; I₀为换算截面惯性矩; β _p为考虑预应力度的折减系数; β ₁为考虑疲劳影响的折减系数; β ₂为考虑截面配筋率的折减系数; M_f为开裂荷载; λ 为预应力度; μ 为纵向钢筋配筋率; n_p为预应力钢筋弹性模量与普通混凝土弹性模量之比; A_p为预应力钢筋面积; A_s为普通钢筋面积。

混凝土规范中开裂前短期刚度计算公式如下:

B=0.85E_cI₀(8)

混凝土规范中带裂缝工作阶段短期刚度计算公式如下:

B= $\begin{matrix} \frac{0.85 E_{c} I_{0}}{κ_{cr} + (1 - κ_{cr}) ω} \end{matrix}$ (9)

κ _cr= $\begin{matrix} \frac{M_{f}}{M_{k}} \end{matrix}$ (10)

ω = $\begin{matrix} (1 + \frac{0.21}{α_{E} ρ}) \end{matrix}$ (1+0.45γ _f)-0.7(11)

γ _f= $\begin{matrix} \frac{(b_{f} - b) h_{f}}{b h_{0}} \end{matrix}$ (12)

式中:α _E为钢筋弹性模量与混凝土弹性模量之比; ρ 为纵向受拉钢筋配筋率; γ _f为受拉翼缘截面面积与腹板有效截面面积的比值; b_f、h_f分别为受拉翼缘的宽度和高度。

3.3 叠合梁跨中挠度计算分析

采用3.1及3.2节规范中方法计算试验梁挠度, 结果汇总于表4。将不同预应力度下典型计算结果绘于图8。

表4 跨中挠度规范计算结果与试验值对比 Table 4 Comparison of calculation results from standard and testing results of mid-span deflectionmm

编号	开裂时						屈服时
编号	试验值 $\begin{matrix} ω_{cr}^{\exp} \end{matrix}$	铁路桥规范 $\begin{matrix} ω_{cr}^{t} \end{matrix}$	混凝土规范 $\begin{matrix} ω_{cr}^{c} \end{matrix}$	$\begin{matrix} \frac{ω_{cr}^{t}}{ω_{cr}^{\exp}} \end{matrix}$	$\begin{matrix} \frac{ω_{cr}^{c}}{ω_{cr}^{\exp}} \end{matrix}$		试验值 $\begin{matrix} ω_{y}^{\exp} \end{matrix}$	铁路桥规范 $\begin{matrix} ω_{y}^{t} \end{matrix}$	混凝土规范 $\begin{matrix} ω_{y}^{c} \end{matrix}$	$\begin{matrix} \frac{ω_{y}^{t}}{ω_{y}^{\exp}} \end{matrix}$	$\begin{matrix} \frac{ω_{y}^{c}}{ω_{y}^{\exp}} \end{matrix}$
S50-2-290	5.26	7.98	3.90	1.52	0.74	23.18		52.65	24.38	2.27	1.05
S50-2-360	6.89	7.61	4.98	1.10	0.72	24.19		36.84	22.52	1.52	0.93
S50-2-430	6.19	6.24	4.61	1.01	0.74	24.74		34.47	23.52	1.39	0.95
S50-3-290	7.65	6.87	6.16	0.90	0.81	26.68		34.49	28.36	1.29	1.06
S50-3-360	7.19	7.31	6.45	1.02	0.90	24.90		34.13	27.59	1.37	1.11
S50-3-430	8.93	7.25	6.69	0.81	0.75	26.49		31.69	26.27	1.20	0.99
S50-4-290	9.71	7.79	8.80	0.80	0.91	31.35		37.68	38.14	1.20	1.22
S50-4-360	10.56	7.44	8.44	0.70	0.80	29.23		36.59	36.52	1.25	1.25
S50-4-430	10.45	6.89	7.89	0.66	0.76	29.27		35.18	35.76	1.20	1.22
S70-3-360	7.55	7.14	6.54	0.95	0.87	22.38		29.16	24.33	1.30	1.09
SNC50-3-0	5.86	5.32	5.20	0.91	0.89	26.61		30.01	23.84	1.13	0.90

表4 跨中挠度规范计算结果与试验值对比 Table 4 Comparison of calculation results from standard and testing results of mid-span deflectionmm

表4和图8分别给出了铁路桥规范和混凝土规范中公式计算值与实测值的对比。可见铁路桥规范只适于计算低预应力度情况下叠合梁弹性段挠度, 混凝土规范只适用于计算低预应力度情况下叠合梁屈服极限挠度, 对于其他情况均存在较大偏差。SNC50-3-0纯NC梁的对比结果说明了规范中利用等效截面刚度法计算短期刚度的有效性。针对于S50-2-290铁路桥规范计算值过大, 有两点需要说明, 其一, 该模型梁预应力度偏小, 导致铁路桥规短期刚度计算公式中考虑疲劳影响的折减系数计算值过小。其二, 该模型梁是第一根试验梁在初始试验过程中加载泵出现问题, 该挠度结果是测得带有损伤模型梁的试验值, 较实际值偏小。

	Figure Option View Download New Window
	图8 规范公式计算结果与试验值对比Fig.8 Comparison of calculation results from standard and testing results

3.4 修正规范中公式后跨中挠度计算

由3.3节中规范计算结果与试验结果的对比可知, 现有规范中的公式并不适用于RPC-NC叠合梁结构, 因此根据试验结果对铁路桥规和混凝土规范中的公式进行修正, 修正后的公式如下:

铁路桥规中开裂前短期刚度计算公式如下:

B=β _pβ _t1E_cI₀(13)

铁路桥规中带裂缝工作阶段短期刚度计算公式如下:

B=β _t1 $\begin{matrix} \frac{β_{p} β_{t 2} M}{β_{t 2} β_{2} M_{f} + β_{p} (M - M_{f})} \end{matrix}$ E_cI₀(14)

混凝土规范中开裂前短期刚度计算公式如下:

B=0.85β _c1E_cI₀(15)

混凝土规范中带裂缝工作阶段短期刚度计算公式如下:

B= $\begin{matrix} \frac{0.85 β_{c 1} E_{c} I_{0}}{κ_{cr} + (1 + κ_{cr}) ω β_{c 2}} \end{matrix}$ (16)

根据3.3节规范计算结果与试验结果的对比, 对规范公式进行修正, 得到修正后公式(13)~(16), 其中铁路桥规修正系数为:

β _t1= $\begin{matrix} \frac{(λ - 0.5) (1.55 - 0.87 λ)}{0.95 λ - 0.45} \end{matrix}$ (17)

β _t2=1.63(0.1+2n_pμ )(18)

式中:β _t1为考虑叠合梁疲劳影响的折减系数; β _t2为考虑叠合梁中钢纤维加入后截面配筋率对刚度的影响系数。

混凝土规范中修正系数 β _c1=0.8, β _c2=0.67。其中, β _c1为考虑叠合梁结构中RPC材料特性系数; β _c2为表征叠合梁下部RPC材料因其致密材料结构和钢纤维作用而特有的高抗拉强度和抵抗开裂变形能力的系数。修正后的计算结果对比见图9, 计算结果对比见表5。

图9和表5给出了规范公式修正后计算值与试验值对比, 其中只有铁路桥规范修正后计算S50-2-290模型梁屈服和极限时挠度计算值与试验值相差较大(误差为40%左右), 其余模型梁计算值与试验值均吻合较好。修正后铁路桥规范在开裂时和屈服时计算值与试验值比值的平均值和标准差分别为0.97、0.13和0.99、0.14。修正后混凝土规范在开裂时和屈服时计算值与试验值比值的平均值和标准差分别为0.99、0.08和0.99、0.08。可见, 修正后的铁路桥规范和混凝土规范公式的计算结果与试验结果吻合良好, 为该新型叠合梁结构的工程应用提供了试验和理论依据。

表5 修正后跨中挠度规范计算值与试验值对比 Table 5 Comparison of calculation results from modified standard and testing results of mid-span deflectionmm

编号	开裂时						屈服时
编号	试验值 $\begin{matrix} ω_{cr}^{\exp} \end{matrix}$	铁路桥规 $\begin{matrix} ω_{cr}^{t} \end{matrix}$	混凝土规范 $\begin{matrix} ω_{cr}^{c} \end{matrix}$	$\begin{matrix} \frac{ω_{cr}^{t}}{ω_{cr}^{\exp}} \end{matrix}$	$\begin{matrix} \frac{ω_{cr}^{c}}{ω_{cr}^{\exp}} \end{matrix}$		试验值 $\begin{matrix} ω_{y}^{\exp} \end{matrix}$	铁路桥规 $\begin{matrix} ω_{y}^{t} \end{matrix}$	混凝土规范 $\begin{matrix} ω_{y}^{c} \end{matrix}$	$\begin{matrix} \frac{ω_{y}^{t}}{ω_{y}^{\exp}} \end{matrix}$	$\begin{matrix} \frac{ω_{y}^{c}}{ω_{y}^{\exp}} \end{matrix}$
S50-2-290	5.26	7.23	4.83	1.37	0.92	23.18		32.36	21.98	1.40	0.95
S50-2-360	6.89	7.07	6.17	1.03	0.90	24.19		23.89	20.87	0.99	0.86
S50-2-430	6.19	5.91	5.71	0.95	0.92	24.74		22.49	21.55	0.91	0.87
S50-3-290	7.65	7.05	7.64	0.92	1.00	26.68		24.62	26.23	0.92	0.98
S50-3-360	7.19	7.40	7.97	1.03	1.11	24.90		24.32	25.67	0.98	1.03
S50-3-430	8.93	7.66	8.36	0.86	0.94	26.49		23.49	24.76	0.89	0.93
S50-4-290	9.71	10.52	10.88	1.08	1.12	31.35		35.61	35.47	1.14	1.13
S50-4-360	10.56	10.16	10.51	0.96	1.00	29.23		31.97	31.41	1.09	1.07
S50-4-430	10.45	9.60	9.87	0.92	0.94	29.27		31.12	30.62	1.06	1.05
S70-3-360	7.55	7.41	8.06	0.98	1.07	22.38		21.63	22.98	0.97	1.03
SNC50-3-0	5.86	5.32	5.20	0.91	0.89	26.61		30.01	23.84	1.13	0.90

表5 修正后跨中挠度规范计算值与试验值对比 Table 5 Comparison of calculation results from modified standard and testing results of mid-span deflectionmm

	Figure Option View Download New Window
	图9 修正后公式计算结果与试验值对比Fig.9 Comparison of calculation results from modified standard and testing results

4 结论

(1)本文测试了10根预应力RPC-NC叠合梁和1根预应力纯NC梁跨中荷载-位移曲线。叠合梁跨中挠度发展可分为以下3个阶段:开裂前弹性阶段、带裂缝工作阶段、普通钢筋屈服后挠度迅速增长阶段。

(2)模型梁试验结果表明:预应力度越高, 跨中荷载-挠度曲线的开裂前弹性段越长, 开裂后的屈服和强化阶段下降得越快; RPC高度对跨中荷载-挠度曲线的开裂前弹性阶段影响不大, 钢筋屈服后随着RPC高度的增加, RPC对裂缝的发展和挠度变形的约束作用增强; 上部NC等级的提高对叠合梁跨中荷载-挠度曲线影响不大; RPC的加入显著提高了预应力RPC-NC叠合梁在弹性工作阶段抗裂和抵抗变形的能力, 同时也提高了梁的极限承载力和极限变形能力。

(3)研究了模型梁跨中挠度计算方法。分别取用铁路桥规范和混凝土规范中短期刚度的计算公式, 与试验结果对比后发现规范中的公式不适用于预应力RPC-NC叠合梁短期挠度的计算。根据试验结果对铁路桥规范和混凝土设计规范中的公式进行了修正, 修正后的计算结果与试验值吻合良好。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Bonnoeau O, Poulin C, Dugat J, et al. Reactive powder concrete: from theory to practice[J]. Concrete International, 1996, 18: 47-49. [本文引用:1]
[2]	Dugat J, Roux N, Bernier G. Mechanical properties of reactive powder concretes[J]. Material and Structure, 1996, 29(5): 233-240. [本文引用:1]
[3]	Habel K, Viviani M, Denarie E. Development of the mechanical properties of an ultra-high performance fiber reinforced concrete[J]. Cement and Concrete Research, 2006, 36(7): 1362-1370. [本文引用:1]
[4]	Voo Y L, Wait K, Stephen J. Shear strength of steel fiber-reinforced ultrahigh-performance concrete beams without stirrups[J]. Journal of Structure Engineering, 2010, 136(11): 1393-1399. [本文引用:1]
[5]	Garas V Y, Kurtis K E, Kahn L F. Creep of UHPC tension and compression: effect of thermal treatment[J]. Cement and Concrete Composites, 2012, 34(4): 493-502. [本文引用:1]
[6]	Yan G, Huang Y, An M Z. Axial compression experimental research of RPC filled steel tube columns[J]. Advanced Materials Research, 2011: 150-151: 198-202. [本文引用:1]
[7]	肖锐, 邓宗才, 兰明章, 等. 不掺硅粉的活性粉末混泥土配合比试验[J]. 吉林大学学报: 工学版, 2013, 43(3): 671-676. Xiao Rui, Deng Zong-cai, Lan Ming-zhang, et al. Experimental research on proportions of reactive powder concrete without silica fume[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(3): 671-676. [本文引用:1]
[8]	闫志刚, 季文玉, 安明喆. 活性粉末混凝土低高度梁设计及试验研究[J]. 土木工程学报, 2009, 42(5): 96-101. Yan Zhi-gang, Ji Wen-yu, An Ming-zhe. Design and experimental study of low-height reactive powder concrete beams[J]. China Civil Engineering Journal, 2009, 42(5): 96-101. [本文引用:1]
[9]	Taylor C W, Montoya K F, Jáuregui D V, et al. Feasibility analysis of using UHPC in prestressed bridge girders[J]. Structures Congress, 2011, 401: 203-214. [本文引用:1]
[10]	季文玉, 丁波, 安明喆. 活性粉末混凝土T形梁抗剪试验研究[J]. 中国铁道科学, 2011, 32(5): 38-42. Ji Wen-yu, Ding Bo, An Ming-zhe. Experimental study on the shear capacity of reactive powder concrete beams[J]. China Railway Science, 2012, 32(5): 38-42. [本文引用:1]
[11]	Cavill B, Chirgwin G. The world̓s first RPC road bridge at Shepherds gully creek, NSW[C]∥The 21st Biennial Conference of the Concrete Institute of Australia, Hobart, 2003: 89-98. [本文引用:1]
[12]	Bierwagen D, Hawash A. Ultra high performance concrete highway bridge[C]∥Proceeding of the Mid-continue Transportation Symposium, Iowa, 2005: 1-14. [本文引用:1]
[13]	季文玉, 过民龙, 李旺旺. RPC-NC组合梁界面受力性能研究[J]. 中国铁道科学, 2016, 37(1): 46-52. Ji Wen-yu, Guo Min-long, Li Wang-wang. Interface mechanical behavior of RPC-NC composite beam[J]. China Railway Science, 2016, 37(1): 46-52. [本文引用:1]
[14]	肖赟, 雷俊卿, 张坤, 等. 多级变幅疲劳荷载下预应力混凝土梁刚度退化[J]. 吉林大学学报: 工学版, 2013, 43(3): 665-670. Xiao Yun, Lei Jun-qing, Zhang Kun, et al. Fatigue stiffness degradation of prestressed concrete beam under multilevel amplitude cycle loading[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(3): 665-670. [本文引用:1]
[15]	张利梅, 赵顺波, 黄承逵. 高性能预应力混凝土梁挠度试验与计算方法[J]. 大连理工大学学报, 2005, 45(1): 96-101. Zhang Li-mei, Zhao Shun-bo, Huang Cheng-kui. Experimentation and calculation of deflection of prestressed high-performance concrete beams[J]. Journal of Dalian University of Technology, 2005, 45(1): 96-101. [本文引用:1]
[16]	GB 50010-201050010-2010. 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2011. [本文引用:2]
[17]	TB 10002B 10002. 3-2005. 铁路桥涵混凝土和预应力混凝土结构设计规范[S]. 北京: 中国铁道出版社, 2010. [本文引用:2]

1996

0.0

... 0 引言活性粉末混凝土(Reactive powder concrete,RPC)作为一种新型高性能混凝土,诞生于20世纪90年代的法国BOUYGUES实验室^[1],自其出现便引起了土建行业科研人员的广泛关注和研究^{[2,3,4,5,6,7]} ...

1996

0.0

2006

0.0

2010

0.0

2012

0.0

2011

0.0

2013

0.0

. 2013, 43(3):671-676 DOI:doi:10.7964/jdxbgxb201303019

Experimental research on proportions of reactive powder concrete without silica fume

不掺硅粉的活性粉末混泥土配合比试验

Xiao Rui , Deng Zong-cai , Lan Ming-zhang

肖锐, 邓宗才, 兰明章

摘　要：在遵循活性粉末混凝土（RPC）基本配制原则的基础上,不掺入硅粉,采用超细水泥、普通水泥、掺合料（粒化高炉矿渣和粉煤灰）、砂、水、减水剂、钢纤维进行配合比试验。试验结果表明：不采用硅粉制备RPC是可行的;在制备RPC时,将超细水泥与适量掺合料混掺后,可以在保证材料强度和流动性的同时提高材料的经济性;用普通水泥取代大部分超细水泥后,材料的性能仍可保证,且更加经济。另外,研究了钢纤维掺量对材料性能（抗压、抗折、流动性及弯曲韧性）的影响规律。

2009

0.0

. 2009, 42(5):96-101

Design and experimental study of low-height reactive powder concrete beams

活性粉末混凝土低高度梁设计及试验研究

Yan Zhi-gang , Ji Wen-yu , An Ming-zhe.

闫志刚, 季文玉, 安明喆

... RPC材料拥有超高的力学性能和耐久性,完全可以满足当前土建行业尤其是桥梁工程的发展需求^[8,9,10],目前在铁路、公路等重大项目中已有应用^[11,12],但由于其制作工艺相对复杂,不能满足当前现场施工要求,大部分构件仍在工厂预制完成 ...

2011

0.0

2011

0.0

. 2011, 32(5):38-42

Experimental study on the shear capacity of reactive powder concrete beams

活性粉末混凝土T形梁抗剪试验研究

Ji Wen-yu , Ding Bo , An Ming-zhe.

季文玉, 丁波, 安明喆

摘　要：通过改变模型试验梁的剪跨比、配箍率和纵筋配筋率,对12根钢筋活性粉末混凝土（RPC）T 形试验梁进行试验,研究活性粉末混凝土T形梁抗剪承载力和破坏形态及主要影响因素。结果表明：与普通混凝土梁相比,活性粉末混凝土T形试验梁具有较高的抗剪承载力和变形能力;剪跨比在1～4范围内时,试验梁的破坏形态表现为斜压和剪压破坏,且与普通混凝土梁的破坏形态有着明显差异;剪跨比、配箍率和纵筋配筋率对试验梁的抗剪承载力影响显著,抗剪承载力随着剪跨比的增大而减小,随配箍率的提高而提高,随纵筋配筋率的增大而增大。

2003

0.0

2005

0.0

2016

0.0

. 2016, 37(1):46-52

Interface mechanical behavior of RPC-NC composite beam

RPC-NC组合梁界面受力性能研究

Ji Wen-yu , Guo Min-long , Li Wang-wang.

季文玉, 过民龙, 李旺旺

... 该结构形式在充分发挥二者材料性能优势的同时,充分利用了二者同为水泥基材料的粘结性能^[13],为保证叠合面粘结强度将原光圆箍筋替换为具有抗剪和抗拉拔能力的螺纹钢筋 ...

2013

0.0

. 2013, 43(3):665-670

Fatigue stiffness degradation of prestressed concrete beam under multilevel amplitude cycle loading

多级变幅疲劳荷载下预应力混凝土梁刚度退化

Xiao Yun , Lei Jun-qing , Zhang Kun

肖赟, 雷俊卿, 张坤

... 桥梁工程中梁结构的挠度一直是工程人员和科研人员关注的重点^[14,15] ...

2005

0.0

. 2005, 45(1):96-101 DOI:doi:10.3321/j.issn:1000-8608.2005.01.020

Experimentation and calculation of deflection of prestressed high-performance concrete beams

高性能预应力混凝土梁挠度试验与计算方法

Zhang Li-mei , Zhao Shun-bo , Huang Cheng-kui.

张利梅, 赵顺波, 黄承逵

进行了配有高强度低松弛钢绞线、预应力比率0.66～1.00、混凝土强度等级C40～C80的14根先张法高性能预应力混凝土梁的加载全过程试验,研究了预应力比率和截面开裂等因素对试验梁挠度的影响. 通过将试验结果与 (GB 50010-2002)相关计算公式对比分析,得出规范变形计算公式对于未开裂梁是适用的,对于预应力比率不大于0.66的梁开裂后也是适用的;随着预应力比率提高,开裂后梁挠度试验值与规范公式计算值的比值逐渐减小,当预应力比率1.00时其比值仅为0.60. 为此,根据试验结果提出了适用于这种高性能预应力混凝土梁的修正的挠度计算方法.

... 桥梁工程中梁结构的挠度一直是工程人员和科研人员关注的重点^[14,15] ...

2011

0.0

... 3 短期刚度及挠度计算方法通过以上叠合梁跨中荷载-挠度曲线的分析以及试验过程中叠合梁接触面未发生滑移可知,RPC-NC叠合梁可采用规范中的方法^[16,17]计算短期挠度 ...

... 本文分别取用《铁路桥涵钢筋混凝土和预应力混凝土结构设计规范》^[16]和《混凝土结构设计规范》^[17]中短期刚度计算方法 ...

2010

0.0

... 本文分别取用《铁路桥涵钢筋混凝土和预应力混凝土结构设计规范》^[16]和《混凝土结构设计规范》^[17]中短期刚度计算方法 ...