三跨独柱连续曲线梁桥抗倾覆稳定性分析

引用本文

宫亚峰, 何钰龙, 谭国金, 申杨凡. 三跨独柱连续曲线梁桥抗倾覆稳定性分析[J].吉林大学学报（工学版）, 2018,48(1): 133-140
GONG Ya-feng, HE Yu-long, TAN Guo-jin, SHEN Yang-fan. Anti-overturning stability analysis for three-span continuous curved girder bridge with single column pier[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 133-140 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161241
Permissions

三跨独柱连续曲线梁桥抗倾覆稳定性分析

宫亚峰, 何钰龙, 谭国金, 申杨凡

吉林大学交通学院,长春 130022

通讯作者：谭国金(1981-),男,副教授,博士.研究方向:桥梁检测与加固.E-mail:tgj@jlu.edu.cn

作者简介:宫亚峰(1977-),男,副教授,博士.研究方向:桥梁结构健康监测理论及应用.E-mail:gongyf@jlu.edu.cn

基金:国家自然科学基金项目(51478203); 吉林省科技厅项目(20140520135H); 中央高校基本科研业务费专项资金项目

摘要

为研究三跨独柱连续曲线梁桥的抗倾覆能力,基于结构倾覆的力学原理并根据桥梁倾覆轴选取原则,推导了微弯桥与弯桥的倾覆轴选取临界方程,比较了弯桥中两类倾覆轴下的抗倾覆稳定性,对三跨独柱连续曲线梁桥的抗倾覆稳定系数进行了验算,并与规范公式计算值进行对比。计算结果表明:在选取弯桥倾覆轴时,根据两中墩支座连线作为倾覆轴进行抗倾覆验算的结果更安全;三跨独柱连续曲线梁桥的抗倾覆稳定系数随曲率半径增大呈现先减小后增大的趋势;对于微弯桥,理论计算值比规范计算值更大;对于弯桥,两者基本一致。

关键词: 桥梁工程; 独柱墩; 曲线梁桥; 抗倾覆稳定性; 曲率半径; 圆心角

中图分类号:U441.2 文献标志码:A 文章编号:1671-5497(2018)01-0133-08

Anti-overturning stability analysis for three-span continuous curved girder bridge with single column pier

GONG Ya-feng, HE Yu-long, TAN Guo-jin, SHEN Yang-fan

College of Transportation, Jilin University, Changchun 130022, China

Abstract

To study the stability of three-span continuous curved girder bridge with single column pier, the overturning axis critical equation of slightly curved bridge and curved bridge is deduced based on the mechanics principle of structure overturning and the selection principle of the bridge overturning axis. The anti-overturning stabilities of curved bridge under two types of overturning axis are compared. The anti-overturning stability coefficient of three-span continuous curved girder bridge with single column pier was checked and compared with the value calculated from standard formula. Calculation results show that, choosing the connecting line of the bearings of two middle piers as the overturning axis, the check is safer. The anti-overturning stability coefficient of the three-span continuous curved girder bridge with single column pier first decreases and then increases with the increase in the curvature radius. For slightly curved bridge, the theoretical calculated value is greater than the value calculated from the standard formula. For curved bridge, both calculated values are basically identical.

Keyword: bridge engineering; single column pier; curved girder bridge; anti-overturning stability; radius of curvature; central angle

Show Figures

0 引言

随着城市交通量的增大, 城市桥梁的建设需求日益增长, 由于三跨独柱连续曲线梁桥具有占地空间小、设计方便、施工成本较低、易于适应周边环境等优势, 成为中国公路以及城市立交桥中最常见的曲线梁桥形式, 尤其是在匝道桥中应用更为广泛。但是独柱墩梁桥相对于多墩梁桥而言, 更容易出现整体性倾覆事故。例如:2015年粤赣高速匝道桥整体侧翻事故、2012年哈尔滨市阳明滩大桥引桥匝道出现了整体侧翻的安全事故以及2011年浙江省上虞春晖互通立交引桥匝道发生整体倾覆事故等^[1]。

国内外专家对桥梁倾覆事故开展了广泛的研究, 造成桥梁倾覆的主要原因是车辆超载及桥梁设计缺陷。曲线梁桥相较于直线梁桥的结构受力形式更为复杂, 曲率半径以及圆心角等特征因素对曲线独柱连续梁桥的抗倾覆能力有较大影响。Zhu等^[2]研究了交通量对I-35W密西西比河大桥坍塌所产生的影响; Kim等^[3]对梁桥的结构稳定性进行了评估; Michaltsos等 $\begin{matrix} {^{}}^{[4]} \end{matrix}$ 研究了桥梁倾覆的数学模型; 周子杰等^[5]讨论了不同支座布置形式、不同曲率半径条件下结构倾覆轴的选取; 曹景等^[6]对箱形截面直线桥及曲线桥的抗倾覆稳定系数计算公式进行了推导; 陈瑶等^[7]给出了抗倾覆稳定安全系数的定义及详细的验算方法, 并建立了抗倾覆稳定安全评价指标体系来反映倾覆破坏的临界状态; 彭卫兵等^[8]构造了一种考虑到箱梁、支座和桥墩间相互作用的抗倾覆承载力实用计算方法; 梁峰^[9]给出了三种情况下三跨独柱连续梁桥抗倾覆度的计算公式。但是, 对于倾覆轴的选取以及在不同形式的倾覆轴下, 三跨独柱连续曲线梁桥的抗倾覆安全系数的验算还不够完整。

本文总结了以往的研究成果, 基于结构倾覆的基本理论, 以圆曲线为例, 探讨了不同曲率半径以及圆心角下, 三跨独柱连续曲线梁桥的倾覆轴选取, 并分情况对其抗倾覆稳定性系数进行了讨论, 采用桥梁实例验算了三跨独柱连续曲线梁桥的抗倾覆稳定性计算公式。

1 桥梁倾覆理论

工程结构之所以发生倾覆, 主要是由于其所受的倾覆力矩超出结构本身所能抵抗的倾覆力矩。因此, 在工程结构设计时, 通常以结构抗倾覆稳定系数k来表示其抗倾覆的安全储备性能, k作为评价其抗倾覆稳定性的重要指标, 是其重要的安全验算指标之一, 根据结构倾覆基本理论, 其抗倾覆稳定系数可表示为:

k= $\begin{matrix} \frac{s_{bk}}{s_{sk}} \end{matrix}$ (1)

式中:k为抗倾覆稳定系数; s_sk为倾覆作用对于倾覆轴的合力矩(倾覆力矩); s_bk为抗倾覆作用对于倾覆轴的合力矩(抗倾覆力矩)。

对于桥梁结构而言, 其抗倾覆力矩主要是由桥梁上部结构自身重力对于倾覆轴所产生的合力矩, 桥梁倾覆力矩主要是翻转侧结构重力以及桥梁上部的活载对倾覆轴产生的合力矩, 根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》^[10](以下简称规范), 对于正交桥梁和斜交角30° 以内的斜交桥梁, 当倾覆轴线为桥梁中心线同侧的桥台外侧支座连线时, 抗倾覆稳定系数计算公式为:

r_qf= $\begin{matrix} \frac{\sum R_{Gi} x_{i}}{(1 + μ) (q_{k} l + P_{k}) e} \end{matrix}$ (2)

式中:r_qf为抗倾覆稳定系数; q_k为车道荷载中的均布荷载; P_k为车道荷载中的集中荷载; l为桥梁全长; e为横向最不利车道位置到倾覆轴的垂直距离; μ 为冲击系数(根据《公路桥涵设计通用规范》^[11]进行计算); R_Gi为成桥状态时各个支座的支座反力; x_i为各个支座到倾覆轴线的垂直距离。

当倾覆轴线为桥台外侧支座和跨中桥墩支座连线时, 抗倾覆稳定系数的计算公式为:

$\begin{matrix} r_{qf}^{'} \end{matrix}$ = $\begin{matrix} \frac{\sum R_{Gi} x_{i}}{(1 + μ) (q_{k} Ω + P_{k} e)} \end{matrix}$ (3)

式中:Ω 为倾覆轴线与横向加载车道围成的面积; e为横向加载车道与倾覆轴线垂直距离的最大值。

2 倾覆轴选取

2.1 倾覆轴选取

根据规范公式对曲线梁桥进行抗倾覆稳定性验算时, 应首先进行倾覆轴选取, 根据结构倾覆理论, 倾覆轴选取的主要原则是:在沿倾覆轴翻转外侧不出现支座的前提下, 同时验算多种可能的倾覆轴, 将倾覆稳定系数较小值所对应的倾覆轴作为设计倾覆轴线。

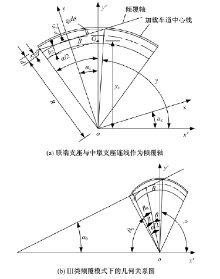
根据以上倾覆轴选取原则, 对于直线梁桥, 由于其倾覆轴必定为两联端外侧支座连线, 因此其抗倾覆稳定性验算均采用式(2), 对于曲线梁桥, 其倾覆轴的确定, 应当根据桥梁的曲率半径和圆心角来进行综合判定。三跨独柱连续曲线梁桥有可能出现3类倾覆模式(见图1):Ⅰ 类:桥梁沿两联端外侧支座连线发生整体倾覆; Ⅱ 类:桥梁沿两中墩连线发生整体倾覆; Ⅲ 类:桥梁沿联端外侧支座与中墩连线发生整体倾覆。

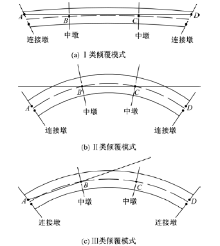	Figure Option View Download New Window
	图1 三跨独柱连续曲线梁桥倾覆模式示意图Fig.1 Overturning mode diagram of three-span continuous curved girder bridge with single column pier

根据不同倾覆模式下选取的倾覆轴不同, 可以将曲线桥梁定义为微弯桥(Ⅰ 类倾覆模式)以及弯桥(Ⅱ 类和Ⅲ 类倾覆模式), 其中微弯桥的倾覆轴与直桥一样, 都是两联端外侧支座的连线, 弯桥的倾覆轴是两中墩支座连线或联端外侧支座与中墩支座连线。

2.2 微弯桥倾覆轴的选取

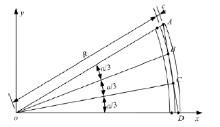
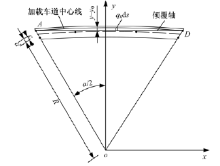
由于微弯桥的倾覆轴与直线桥梁一致, 均为两联端外侧支座连线, 因此由弯桥过渡到微弯桥, 其临界状态是曲线在一定曲率半径以及圆心角下, 使得桥梁最外侧中墩支座与联端外侧支座在同一水平线上。对于常见的三跨独柱连续曲线梁桥, 考虑等跨布置, 令两中墩支座与联端外侧支座在同一水平线上(见图2), 根据四点共线时, BD线段与CD线段的斜率相等的条件, 可推导出微弯桥与弯桥倾覆轴选取的临界方程如下:

	Figure Option View Download New Window
	图2 临界方程计算简图Fig.2 Calculating diagram of critical equation

$\begin{matrix} \frac{Rsin \frac{α}{3} - 0}{Rcos \frac{α}{3} - (R + c)} \end{matrix}$ = $\begin{matrix} \frac{Rsin \frac{2 α}{3} - 0}{Rcos \frac{2 α}{3} - (R + c)} \end{matrix}$ (4)

式中:R为桥梁中心线半径; α 为圆心角; c为联端支座到桥梁中心线的距离。

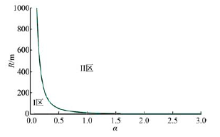
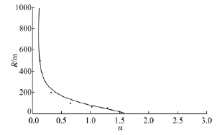
基于常见匝道桥的设计参数, 令c=1.5, 根据式(4)绘出关于α (本文中按弧度制表示)与R的微弯桥倾覆轴选取隐函数图像如图3所示, 可以将此图作为微弯桥与弯桥倾覆轴选取的判定图样, 若桥梁设计参数α 与R处于隐函数图线的左侧区域(Ⅰ 区), 则按照微弯桥进行设计; 若桥梁设计参数α 与R处于隐函数图线的右侧区域(Ⅱ 区), 则按照弯桥进行设计。

	Figure Option View Download New Window
	图3 倾覆轴选取判定图Fig.3 Decision of selection of overturning axis

根据图3可以看出, 临界方程隐函数图线随α 与R的增长呈现出双曲线变化趋势, 在大多数情况下按照Ⅱ 区情况进行选取; 且两类倾覆模式的界定主要与设计参数α 有关。当α > 0.5时, 倾覆轴主要按照弯桥选取; 当α < 0.2时, 倾覆轴主要按照微弯桥选取; 当0.2< α < 0.5时, R较小时倾覆轴按微弯桥选取, R较大时倾覆轴按照弯桥选取。

2.3 弯桥倾覆轴的选取

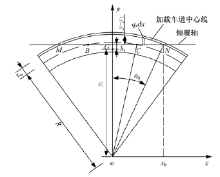
根据图3判定桥梁倾覆轴线按照弯桥进行选取时, 应当考虑Ⅱ 类倾覆模式或者Ⅲ 类倾覆模式, 此时需要同时验算两类倾覆模式的抗倾覆稳定系数, 按照最不利情况即抗倾覆稳定系数较小的情况进行倾覆轴选取。对于三跨独柱连续曲线梁桥, 为比较两类倾覆模式下的抗倾覆稳定系数, 考虑均布荷载为活载加载工况, 计算简图如图4、图5所示。

	Figure Option View Download New Window
	图4 Ⅱ 类倾覆模式下的计算简图Fig.4 Calculating diagram of Ⅱ class overturning mode

	Figure Option View Download New Window
	图5 Ⅲ 类倾覆模式下的计算简图Fig.5 Calculating diagram of Ⅲ class overturning mode

根据式(1)分别推导出两类倾覆模式下的抗倾覆稳定系数, 采用曲线梁桥结构上部重力对其重心取矩作为桥梁的抗倾覆力矩, 将均布荷载布置在桥梁的最不利位置上, 使其对倾覆轴产生的倾覆力矩最大, 两者比值即为抗倾覆稳定系数。Ⅱ 类倾覆模式下的抗倾覆稳定系数如式(5)所示, Ⅲ 类倾覆模式下的抗倾覆稳定系数如式(6)所示, 曲线桥梁的重心公式(假设该曲线桥梁的质量均匀分布)如式(7)所示, 由于计算所得后一项值较小, 在偏安全考虑的前提下可以简化计算, 忽略后一项计算值。将加载车道中心线上的微元对倾覆轴取矩, 并进行曲线积分(通过几何关系得出积分上、下限), 即可得到M_q₁的计算过程如式(8)所示, 通过几何关系可以得到h₁如式(9)所示; 同理可得Ⅲ 类倾覆模式下M_q₂的计算过程如式(10)(11)所示, 积分上、下限的计算过程如式(12)(13)(14)所示, h₂如式(15)所示。

k₁= $\begin{matrix} \frac{s_{bk 1}}{s_{sk 1}} \end{matrix}$ = $\begin{matrix} \frac{G h_{1}}{{M_{q}}_{1}} \end{matrix}$ (5)

k₂= $\begin{matrix} \frac{s_{bk 2}}{s_{sk 2}} \end{matrix}$ = $\begin{matrix} \frac{G h_{2}}{M_{q 2}} \end{matrix}$ (6)

y_c= $\begin{matrix} \frac{2 Rsin \frac{α}{2}}{α} \end{matrix}$ + $\begin{matrix} \frac{2 d^{2} \sin \frac{d}{2}}{3 Rα} \end{matrix}$ ≈ $\begin{matrix} \frac{2 Rsin \frac{α}{2}}{α} \end{matrix}$ (7)

M_q₁=q_k∫ _L(y-y₁)ds=2q_k $\begin{matrix} \int_{0}^{x} \end{matrix}$ (y-y₁) $\begin{matrix} \sqrt[]{1 + y'^{2}} \end{matrix}$ dx=2q_kR² $\begin{matrix} (1 + \frac{d}{R}) \end{matrix}$ [ $\begin{matrix} \sqrt[]{{(1 + \frac{d}{R})}^{2} - co s^{2} \frac{α}{6}} \end{matrix}$ -α ₀cos $\begin{matrix} \frac{α}{6} \end{matrix}$ ] (8)

h₁=|y_c-y₁|= $\begin{matrix} |\frac{2 Rsin \frac{α}{2}}{α} - Rcos \frac{α}{6}| \end{matrix}$ (9)

M_q₂=q_k∫ _L(y-y₂)ds=q_k $\begin{matrix} \int_{γ}^{-} \end{matrix}$ (y-y₂)(R+d)dθ (10)

M_q₂=q_k(R+d)² $\begin{matrix} [\cos (γ - α_{x}) + \frac{}{} \end{matrix}$ sin $\begin{matrix} (\frac{α}{2} - α_{x}) \end{matrix}$ ]-q_k(R+c)(R+d)×

$\begin{matrix} (\frac{π}{2} + \frac{α}{2} - γ) \end{matrix}$ cos $\begin{matrix} (\frac{α}{2} - α_{x}) \end{matrix}$ (11)

α _x=arctan $\begin{matrix} \frac{\cos \frac{α}{6} - (1 + \frac{c}{R}) \cos \frac{α}{2}}{(1 + \frac{c}{R}) \sin \frac{α}{2} - \sin \frac{α}{6}} \end{matrix}$ (12)

γ = $\begin{matrix} \frac{π}{2} \end{matrix}$ +α _x-β = $\begin{matrix} \frac{π}{2} \end{matrix}$ +α _x-arccos $\begin{matrix} \frac{(R + c) \cos β_{0}}{(R + d)} \end{matrix}$ (13)

β ₀= $\begin{matrix} \frac{π}{2} \end{matrix}$ -α _x-θ ₀= $\begin{matrix} \frac{π}{2} \end{matrix}$ -α _x- $\begin{matrix} (\frac{π - α}{2}) \end{matrix}$ (14)

h₂=|y_ccosα _x-y₂|= $\begin{matrix} |\frac{2 Rsin \frac{α}{2}}{α} \cos α_{x} - (R + c) \cos (\frac{α}{2} - α_{x})| \end{matrix}$ (15)

式中:y_c为曲线桥梁重心到圆心的距离; d为曲线桥梁中心线到加载车道中心线的距离; y为加载车道中心线的纵坐标; $\begin{matrix} {M_{q}}_{1} \end{matrix}$ 为Ⅱ 类倾覆模式下的倾覆力矩; h₁为Ⅱ 类倾覆模式下曲线桥梁重心到倾覆轴的垂直距离; y₁为Ⅱ 类倾覆模式下倾覆轴的纵坐标; $\begin{matrix} {M_{q}}_{2} \end{matrix}$ 为Ⅲ 类倾覆模式下的倾覆力矩; h₂为Ⅲ 类倾覆模式下曲线桥梁重心到倾覆轴的垂直距离; y₂为Ⅲ 类倾覆模式下倾覆轴的纵坐标。

根据上述公式可以计算得出弯桥在两类不同倾覆模式下的抗倾覆稳定系数, 在选取两种不同倾覆轴时, G以及q_k是相同的, 因此在仅比较两种抗倾覆稳定系数大小的情况下, 为简化计算, 可将相同的量进行约分, 考虑常见曲线桥的桥宽(双车道、四车道、六车道), 令d和c取不同的值(d=2.1、4.2、6.3 m; c=1.5、3.0、4.5 m), 绘出三跨独柱连续曲线梁桥的抗倾覆稳定系数k随着曲率半径及圆心角的变化趋势如图6所示。

如图6所示, 随着圆心角的增大, 两类倾覆轴线下桥梁抗倾覆稳定性的基本趋势是增长的, 两中墩支座连线作为桥梁倾覆轴线(Ⅱ 类倾覆模式)时, 其抗倾覆稳定系数值k₁随着圆心角的增大变化较为明显, 联端支座与中墩支座连线作为桥梁倾覆轴线(Ⅲ 类倾覆模式)时, 其抗倾覆稳定系数值k₂随着圆心角的增大变化趋势较弱; 当圆心角相同时, 半径对两类倾覆轴下的桥梁抗倾覆稳定性的影响较小, 两种倾覆下的抗倾覆稳定系数随着车道数的增多呈现下降趋势, 且变化值随圆心角的增加更趋平缓。从图6可以看出, 当两中墩支座连线作为桥梁倾覆轴线时, 对于不同车道数的三跨独柱连续曲线梁桥, 其抗倾覆稳定系数值k₁均小于k₂, 尤其是在α 值较大时, 两者差距尤为明显, 说明用两中墩支座连线作为桥梁抗倾覆稳定系数验算更安全。

	Figure Option View Download New Window
	图6 两类倾覆轴下的抗倾覆稳定系数Fig.6 Anti-overturning stability coefficient of two types of overturning axis

3 曲线桥抗倾覆稳定性验算

3.1 微弯桥抗倾覆稳定性验算

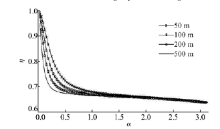
对于微弯桥, 由于其倾覆轴是两联端支座连线, 根据规范进行抗倾覆稳定性验算, 应按照式(2)进行计算, 计算简图如图7所示, 对于曲线桥梁而言, 主要的计算差别在于均布活载所引起的倾覆力矩部分, 根据几何关系可知, 在规范中这一部分所产生的倾覆力矩如式(16)所示, 根据几何关系和力学原理, 其在均布荷载中所产生的实际倾覆力矩的计算过程如式(17)(18)所示, 最终通过理论计算得到不同半径下微弯桥在均布荷载下产生的倾覆力矩值与规范值的比值η 如图8所示。

	Figure Option View Download New Window
	图7 微弯桥抗倾覆系数计算简图Fig.7 Calculating diagram of anti-overturning coefficient of slightly curved bridge

	Figure Option View Download New Window
	图8 不同半径下微弯桥的η 值Fig.8 η of slightly curved bridge with various radius

q_kle=q_k(R+d)α [(R+d)-(R+c)cos $\begin{matrix} \frac{α}{2} \end{matrix}$ ](16)

M_q₀=q_k∫ _Ly-y₀ds=2q_k $\begin{matrix} \int_{\frac{π}{2}}^{-} \end{matrix}$ [(R+d)sinθ -(R+c)· cos $\begin{matrix} \frac{α}{2} \end{matrix}$ ](R+d)dθ (17)

M_q₀=2q_k(R+d)[(R+d)sin $\begin{matrix} \frac{α}{2} \end{matrix}$ -(R+c)· $\begin{matrix} \frac{α}{2} \end{matrix}$ cos $\begin{matrix} \frac{α}{2} \end{matrix}$ ](18)

式中: $\begin{matrix} {M_{q}}_{0} \end{matrix}$ 为Ⅰ 类倾覆模式下的倾覆力矩; y₀为Ⅰ 类倾覆模式下倾覆轴的纵坐标。

根据图8所示, 随着α 的增大, 不同半径下的η 值均小于1并出现了下降的趋势, 且下降趋势是先急后缓的。在α 小于0.5时, η 值的下降趋势较快; 在α 大于0.5时, η 值的下降趋势较为缓和, 这说明采用规范公式所计算得到的倾覆力矩值更大, 最终所得的抗倾覆稳定系数值更小, 其验算结果更安全, 且圆心角越大, 运用规范公式进行验算更为安全。当α 小于1时, 曲线梁桥的半径越小, η 值越大; 当α 大于1时, 不同半径下的η 值随着α 的增长趋于一致。由于微弯桥的α 值基本都小于1, 因此采用大半径的曲线参数设计并运用规范计算公式进行验算更安全。

3.2 弯桥抗倾覆稳定性验算

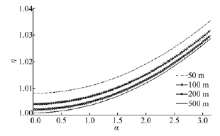
与微弯桥类似, 弯桥抗倾覆稳定系数验算计算公式与规范计算公式相比, 其主要差别也在于均布荷载部分所产生的倾覆力矩, 采用定积分对所围面积进行计算, 如式(19)所示。根据第2节所得结论, 当采用两中墩支座连线作为倾覆轴线(Ⅱ 类倾覆模式)进行抗倾覆稳定性验算是更安全的, 因此仅运用Ⅱ 类倾覆模式进行验算。根据式(3)规范中对于均布荷载所产生的桥梁倾覆力矩为q_kΩ , 其计算简图如图9所示, 经过理论计算, 其实际所产生的倾覆力矩如式(10)~式(15)所示, 代入典型曲线匝道桥的基本参数(c=1.5、d=2.1), 计算不同半径下弯桥在均布荷载下产生的倾覆力矩值与规范值的比值η 如图10所示。

q_kΩ =2q_k $\begin{matrix} \int_{0}^{x_{0}} \end{matrix}$ y-y₁dx=q_k[(R+d)²(sinθ cosθ -θ + $\begin{matrix} \frac{π}{2} \end{matrix}$ )-2Rx₀cos $\begin{matrix} (\frac{α}{6}) \end{matrix}$ ](19)

	Figure Option View Download New Window
	图9 弯桥抗倾覆稳定系数计算简图Fig.9 Calculating diagram of anti-overturning stability coefficient of curved bridge

	Figure Option View Download New Window
	图10 不同半径下弯桥的η 值Fig.10 η of curved bridge with various radius

θ =arccos $\begin{matrix} \frac{x_{0}}{R + d} \end{matrix}$ =arccos $\begin{matrix} \frac{\sqrt[]{{(R + d)}^{2} - {(R \cdot \cos \frac{α}{6})}^{2}}}{R + d} \end{matrix}$ (20)

从图10可以看出, 圆心角与曲率半径对三跨独柱连续曲线梁桥抗倾覆稳定系数均产生影响, 其中圆心角α 的影响效果更明显。随着α 的增大, 不同半径下η 值均大于1并出现了非线性上升的趋势, 这说明采用规范公式所计算得到的倾覆力矩值更小, 最终所得的抗倾覆稳定系数值更大, 其验算结果不安全, 且随着圆心角变大, 运用规范公式进行抗倾覆稳定性验算结果更不安全。当α 值一定时, 曲线梁桥的半径越小, η 值越大, 因此采用大半径的曲线参数设计并运用规范计算公式进行验算是更安全的。但η 值随着α 和R的增大总体变化幅度并不大, 因此尽管运用规范公式验算所计算得到的抗倾覆稳定系数稍大(1< η < 1.04), 但与实际值相比非常接近, 可以近似采用规范公式进行验算。

3.3 实例计算

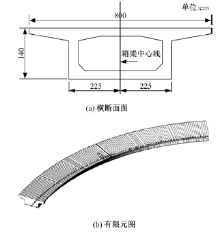
选用长春市某三跨独柱曲线连续箱梁匝道桥为计算实例, 其横断面如图11(a)所示, 该桥设计参数如下:桥梁采用三跨等跨设计, 每跨长为21.5 m, 桥梁曲率半径为63.5 m, 圆心角为1.02, 桥面铺装厚度为17 cm, 桥面铺装材料的容重为22.5 kN/m³。建立相对应桥梁有限元模型如图11(b)所示。

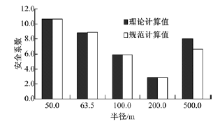
	Figure Option View Download New Window
	图11 桥梁实例计算图Fig.11 Calculating diagram of bridge model

在其余条件不变的情况下, 通过控制跨径相等, 仅改变桥梁的曲率半径R值, 首先对桥梁类型进行判定, 以选取桥梁倾覆轴(见图12), 根据规范设定工况对桥梁的抗倾覆稳定系数进行计算, 计算得到的理论值与规范值如图13所示。

	Figure Option View Download New Window
	图12 倾覆轴选取图Fig.12 Selection of overturning axis based on design parameters

	Figure Option View Download New Window
	图13 不同半径下抗倾覆稳定系数对比图Fig.13 Comparison of anti-overturning stability coefficient with various radius

根据图13可以看出, 桥梁抗倾覆稳定系数随着半径的增大出现了先减小后增大的现象, 这是由于当桥梁曲率半径增大到一定临界值时, 桥梁的倾覆轴发生了改变, 相同类型的桥梁随着半径的增大, 其抗倾覆稳定系数是不断减小的。当桥梁为弯桥时, 理论计算结果比规范值稍小, 最大差值仅为0.062, 当半径为500 m时, 桥梁属于微弯桥, 理论计算值比规范计算结果大17.3%, 此时运用规范公式进行验算是安全的, 实例计算结果与以上验算结论是一致的。

4 结论

(1)在桥梁倾覆轴线外侧不能出现支座, 这是倾覆轴选取的基本原则, 通过计算各个倾覆轴可能产生的抗倾覆稳定系数, 发现对于三跨独柱曲线连续箱梁而言, 两中墩支座连线作为倾覆轴时, 其抗倾覆稳定系数始终最小。

(2)与规范结果相比, 三跨独柱曲线连续箱梁计算的实际抗倾覆稳定系数与倾覆轴的选取有关, 按微弯桥选取时, 理论计算值比规范计算结果大17.3%, 因此采用规范公式进行验算的值更安全, 按弯桥选取时, 采用规范公式进行验算的值稍大, 最大差值仅为0.062。

(3)根据实例计算结果, 在一定曲率半径范围内(50~500 m), 随着三跨独柱曲线连续箱梁曲率半径从50 m增加到200 m, 桥梁的抗倾覆稳定系数呈现出减小的趋势, 因此小半径桥的抗倾覆稳定性更好, 当曲率半径继续增大到500 m, 出现了倾覆轴突变, 使得抗倾覆稳定系数变大。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Xu F Y, Zhang M J, Wang L, et al. Recent highway bridge collapses in China: review and discussion[J]. Journal of Performance of Constructed Facilities, 2016, 30(5): 1-6. [本文引用:1]
[2]	Zhu S, Levinson D, Liu H X, et al. The traffic and behavioral effects of the I-35W Mississippi River bridge collapse[J]. Transportation Research Part A: Policy & Practice, 2008, 44(44): 771-784. [本文引用:1]
[3]	Kim E S, Kim J H. Evaluation of the structure stability of a plate girder bridge using MIDAS structure analysis[J]. Transactions of the Korean Society of Mechanical Engineers A, 2014, 38(4): 451-457. [本文引用:1]
[4]	Michaltsos G T, Raftoyiannis I G. A mathematical model for the rocking, overturning and shifting problems in bridges[J]. Engineering Structures, 2008, 30(12): 3587-3594. [本文引用:1]
[5]	周子杰, 阮欣, 石雪飞. 梁桥横向稳定验算中倾覆轴的选取[J]. 重庆交通大学学报: 自然科学版, 2013, 32(5): 907-910. Zhou Zi-jie, Ruan Xin, Shi Xue-fei. Selection of overturning axis in lateral stability calculation of girder bridge[J]. Journal of Chongqing Jiaotong University (Natural Science), 2005, 32(5): 907-910. [本文引用:1]
[6]	曹景, 刘志才, 冯希训. 箱形截面直线桥及曲线桥抗倾覆稳定性分析[J]. 桥梁建设, 2014, 44(3): 69-74. Cao Jing, Liu Zhi-cai, Feng Xi-xun. Analysis of overturning stability of straight and curved bridges with box sections[J]. Bridge Construction, 2014, 44(3): 69-74. [本文引用:1]
[7]	陈瑶, 陈露晔, 张建华. 独柱墩桥梁抗倾覆稳定验算方法及参数影响分析[J]. 浙江交通职业技术学院学报, 2013, 14(3): 1-6. Chen Yao, Chen Lu-ye, Zhang Jian-hua. Calculation method of anti-overturning stability and analysis of influence of parameters on single column bridge[J]. Journal of Zhejiang Institute of Communications, 2013, 14(3): 1-6. [本文引用:1]
[8]	彭卫兵, 徐文涛, 陈光军, 等. 独柱墩梁桥抗倾覆承载力计算方法[J]. 中国公路学报, 2015, 28(3): 66-72. Peng Wei-bing, Xu Wen-tao, Chen Guang-jun, et al. Calculation method for anti-overturning capacity of single column pier girder bridge[J]. China Journal of Highway and Transport, 2015, 28(3): 66-72. [本文引用:1]
[9]	梁峰. 三跨独柱连续梁桥抗倾覆能力研究[J]. 公路, 2009(10): 40-43. Liang Feng. Research on the anti-overturning ability of three-span continuous girder bridge with single column pier[J]. Highway, 2009(10): 40-43. [本文引用:1]
[10]	JTG D62-2012. 公路钢筋混凝土及预应力混凝土桥涵设计规范(征求意见稿)[S]. JTG D60-2015. 公路桥涵设计通用规范[S]. [本文引用:1]

2016

0.0

... 例如:2015年粤赣高速匝道桥整体侧翻事故、2012年哈尔滨市阳明滩大桥引桥匝道出现了整体侧翻的安全事故以及2011年浙江省上虞春晖互通立交引桥匝道发生整体倾覆事故等^[1] ...

2008

0.0

... Zhu等^[2]研究了交通量对I-35W密西西比河大桥坍塌所产生的影响 ...

2014

0.0

... Kim等^[3]对梁桥的结构稳定性进行了评估 ...

2008

0.0

2013

0.0

. 2013, 32(5):907-910 DOI:doi:10.3969/j.issn.1674-0696.2013.05.02

Selection of overturning axis in lateral stability calculation of girder bridge

梁桥横向稳定验算中倾覆轴的选取

Zhou Zi-jie , Ruan Xin , Shi Xue-fei.

周子杰, 阮欣, 石雪飞

摘　要：基于目前工程中采用倾覆稳定系数对梁桥横向稳定进行验算的方法,讨论了不同支座布置形式、不同曲率半径条件下结构倾覆轴的选取。理论推导和有限元计算结果表明:联端外侧两支座连线外无支座的直线梁桥和大曲率半径的曲线梁桥,倾覆轴应选取该连线;联端外侧两支座连线外有支座的曲线梁桥,倾覆轴应选取跨中位置相邻两跨外侧支座的连线。

... 周子杰等^[5]讨论了不同支座布置形式、不同曲率半径条件下结构倾覆轴的选取 ...

2014

0.0

. 2014, 44(3):69-74

Analysis of overturning stability of straight and curved bridges with box sections

箱形截面直线桥及曲线桥抗倾覆稳定性分析

Cao Jing , Liu Zhi-cai , Feng Xi-xun.

曹景, 刘志才, 冯希训

... 曹景等^[6]对箱形截面直线桥及曲线桥的抗倾覆稳定系数计算公式进行了推导 ...

2013

0.0

. 2013, 14(3):1-6 DOI:doi:10.3969/j.issn.1671-234X.2013.03.001

Calculation method of anti-overturning stability and analysis of influence of parameters on single column bridge

独柱墩桥梁抗倾覆稳定验算方法及参数影响分析

Chen Yao , Chen Lu-ye , Zhang Jian-hua.

陈瑶, 陈露晔, 张建华

针对独柱墩桥梁倾覆倒塌时有发生的现状,从现行相关规范的局限出发,给出了抗倾覆稳定安全系数的定义及详细的验算方法,适用于工程抗倾覆稳定验算。通过对桥宽、梁端支座间距、曲率半径、联长等影响参数进行有限元数值分析,得到了独柱墩抗倾覆稳定安全系数随以上参数改变而变化的规律,并以此建立了能够较为全面的反映倾覆破坏临界状态的抗倾覆稳定安全评价指标体系。

... 陈瑶等^[7]给出了抗倾覆稳定安全系数的定义及详细的验算方法,并建立了抗倾覆稳定安全评价指标体系来反映倾覆破坏的临界状态 ...

2015

0.0

. 2015, 28(3):66-72

Calculation method for anti-overturning capacity of single column pier girder bridge

独柱墩梁桥抗倾覆承载力计算方法

Peng Wei-bing , Xu Wen-tao , Chen Guang-jun

彭卫兵, 徐文涛, 陈光军

In order to find out the failure mechanism and propose effective calculation method for anti-overturning capacity of single column pier girder bridge, a practical calculation method for anti-overturning capacity was constructed with the interactions among box girder, bearing and pier considered. With the geometric nonlinear and contact nonlinear considered, the finite element model for anti-overturning capacity of single column pier girder bridge was established. A comparative study between the practical calculation method and the finite element model was conducted on Chunhui Bridge, and the calculation results were validated by the load measured in the collapse site of Chunhui Bridge. The results show that the anti-overturning moment of single column pier girder bridge includes the moment around the rotation center generated by self weight and support reaction in end position; the overturning ultimate loads with the practical calculation method and the finite element simulation are proved in good agreement with the measured load in the collapse site of Chunhui Bridge. The correctness of the practical calculation method and the finite element model are proved to be correct. The linear gravity of the super structure has significant effect on anti-overturning capacity of structures.

为了明确独柱墩梁桥的破坏机理并提出有效的抗倾覆承载力计算方法,基于箱梁、支座和桥墩三者之间的相互作用关系,构造了抗倾覆承载力实用计算方法,并通过考虑几何非线性和接触非线性,建立了独柱墩梁桥抗倾覆计算的有限元模型.对上虞春晖大桥采用实用计算和建立有限元模型方法进行了对比研究,并与倒塌现场实际倾覆荷载进行了对比验证.研究结果表明:独柱墩梁桥抗倾覆力矩包括上部结构自重和端部支座反力对转动中心的力矩;采用实用计算方法和有限元模拟得到的倾覆极限荷载与春晖桥现场倒塌实测荷载均较为吻合,验证了实用计算方法和有限元模型的正确性;上部结构线重度对结构抗倾覆有显著影响.

... 彭卫兵等^[8]构造了一种考虑到箱梁、支座和桥墩间相互作用的抗倾覆承载力实用计算方法 ...

0.0

. , 2009(10):40-43

Research on the anti-overturning ability of three-span continuous girder bridge with single column pier

三跨独柱连续梁桥抗倾覆能力研究

Liang Feng.

梁峰

通过对独柱连续箱梁桥的抗倾覆能力分析,分三种情况给出抗倾覆度的计算公式,并由此推导出对应三种情况最小支座间距的计算式,并从中理论验证了该种桥型发生倾覆的特点和因素.

... 梁峰^[9]给出了三种情况下三跨独柱连续梁桥抗倾覆度的计算公式 ...

0.0

... 对于桥梁结构而言,其抗倾覆力矩主要是由桥梁上部结构自身重力对于倾覆轴所产生的合力矩,桥梁倾覆力矩主要是翻转侧结构重力以及桥梁上部的活载对倾覆轴产生的合力矩,根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》^[10](以下简称规范),对于正交桥梁和斜交角30#cod#x000b0 ...