近30年来, 国内外建成的连续刚构桥普遍出现不同程度的梁体下挠过大、混凝土裂缝过宽的问题。由于设计理念、施工水平受当时条件的限制, 桥梁建成后主梁下挠的幅度是相当大的, 特别是对于主跨200 m以上的混凝土连续刚构桥, 后期下挠有的已接近跨径的1%。跨中下挠会进一步加剧箱梁底板开裂, 而箱梁梁体裂缝增多将使结构刚度降低, 从而进一步加剧了跨中下挠, 这两者相互影响, 形成了恶性循环。箱梁典型裂缝位于边跨现浇段、支座附近、跨中腹板(斜裂缝)以及顶底板(纵向裂缝及横向裂缝), 这些裂缝及下挠的存在严重影响到桥梁的使用性能, 致使桥梁结构的动力性能降低。若不及时维护, 可能造成主体结构的破坏。科巴桥^[1]是一座跨中带铰的三跨预应力混凝土连续刚构桥, 其跨径组合为(72+241+72) m, 是当时世界上同类桥梁中跨度最大者。其1978年建成通车, 通车后不久就产生了较大的挠度, 到1990年, 其挠度达到1.2 m。后来采用体外索施加预应力, 使主跨中央挠度减小。1996年其加固处理后不到3个月就发生了倒塌事故。由此可知, 受到当时计算条件的限制, 平面杆系模型对病害成因分析不全面, 且加固不是从主应力加固角度出发而是一味地提高连续刚构桥的承载力和增加主梁压应力, 用体外预应力加固提高(主)拉应力指标的同时, 还要注意(主)压应力是否超标从而造成梁体混凝土压碎的灾害, 例如科巴桥的倒塌, 造成巨大损失。

目前, 常用的加固方式有:粘贴钢板、FRP材料、碳纤维布、预应力碳纤维板、体外预应力等^{[2, 3, 4, 5, 6]}。从施工难度和效率来看, 体外预应力束的方式是提高抗弯、抗剪承载力及抗裂比较理想的方式。设计中通常采用平面杆系模型、空间杆系模型、平面梁格法或局部实体分析相结合的方法。但是, 空间杆系模型缺乏对空间效应的精细化分析, 平面梁格法在满足工程精度的条件下, 是一种既方便又适用的有限元设计分析手段, 为工程技术人员提供了很大方便, 但是由于其等效原理的近似性, 计算结果不能准确反映诸如箱型结合梁截面的剪应力分布。采用实体分析进行补充计算难以与总体计算完全结合, 也难以配合施工阶段、徐变收缩、活载加载等设计要求的计算, 而且分析结果是各种变形下的总体应力结果, 与现行规范的内力配筋设计方法不匹配, 很难有针对性地加强构造配筋^[2]。可见, 运用传统的分析方法无法完全反应混凝土梁桥的各个受力特点, 同时又无法解决混凝土梁桥设计的关键问题。因而需要突破单梁分析和设计的传统方法, 运用更加全面的分析方法进行受力分析和设计, 在完成结构内力和应力分析的同时, 结合现有规范完成结构的配筋设计工作^[3]。

文献[4, 5]讲述并应用了实用精细化分析方法— — 空间网格模型。网格模型将箱梁截面视为由若干块板组成, 对每一块板进行梁格划分, 用划分后的梁格来等效代替每块板的受力。相比梁格法, 空间网格划分更加精细化。由于将顶板划分得更密, 可以分析出顶板的各梁格在剪力滞效应下的应力, 且不用计算有效宽度。刚性扭转通过空间网格之间的相互共同作用反映在各个梁格的剪应力上, 同样可以实现在荷载作用下截面的畸变分析及截面各个板件的横向弯曲变形。它能够分析箱梁截面在偏心荷载作用下的各种变形形态。空间网格模型输出的结果是各个梁格的内力、应力及位移, 可以方便得到结构不同部位的受力状态, 从而有针对性地加强构造配筋, 对实际工程的设计分析有重要意义。

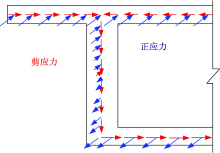
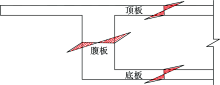
对于一个典型的预应力混凝土箱梁桥, 结构在外荷载作用下的受力效应不再以分别代表顶板上缘和底板下缘的“ 截面上下缘应力” 及腹板的面内主应力作为验算应力来表示, 而是每一个组成板件(箱梁的顶板、底板和腹板)的上缘、下缘和面内主应力都值得关注, 从而用每一个关注的验算应力可以反映该位置的受力情况及可能发生的开裂情况^[7]。表1列出了一个箱梁结构需要关注的完整的验算应力, 同时列出相应验算应力所对应的裂缝形式, 表中还反应出产生这些应力的结构效应和各构件及构件各方向的设计受力状态, 其中黑斜体字为现行设计计算方法通常关注的应力验算。因此, 加固时不仅要关注正应力, 还要关注主拉应力和主压应力, 这样可以全面分析结构病害的成因, 由此针对性地进行加固^[8]。

表1

Table 1

表1(Table 1)

表1 一个混凝土单箱单室箱梁截面的完整验算应力 Table 1 Complete section checking stress of concrete single cell box girder 关注的验算应力 部位 对应裂缝 产生应力的主要结构效应 设计受力状态 顶板纵向面 外正应力 上缘 主要反映结构的整体受弯效应。 配置纵向预应力, 可以使混凝土在该方向不出现拉应力, 即可达到全预应力状态。 下缘 顶板横向面 外正应力 上缘 桥面板的受力特征可视作横向单向板, 故主要承受局部效应, 包括车辆活载。 配置横向预应力, 可以使混凝土在该方向不出现拉应力, 即可达到全预应力状态。 下缘 顶板面内 主应力 板厚方向 主要反映结构的整体效应(弯、剪、扭)。 一般主拉应力难以消除, 为部分预应力或钢筋混凝土受力状态。 底板纵向面 外正应力 上缘 主要反映结构的整体受弯效应, 以及预应力钢束锚固力产生的局部效应。 一般为全预应力。但若底板锚固设计不合理, 则局部区域为钢筋混凝土受力状态。 下缘 底板横向面 外正应力 上缘 产生横向面外应力的箱梁畸变效应很小, 故一般很少关注。但在变截面梁底板内布置的纵向预应力钢束会对底板产生“ 外崩力” 。 箱梁底板横向一般是不配预应力的, 所以底板的面外受力方向是钢筋混凝土受力状态。 下缘 底板面内 主应力 板厚 方向 主要反映结构的整体效应(弯、剪、扭), 以及底板预应力钢束锚固产生的面内剪应力。 一般底板的面内受力方向是钢筋混凝土受力状态。 腹板面外 正应力 内侧 腹板面外应力由箱梁畸变或内外侧温差产生, 但效应不大, 故一般很少关注。 腹板面外受力方向是钢筋混凝土受力状态。 外侧 腹板面内 主应力 板厚 方向 主要反映结构的整体效应(弯、剪、扭)。 配竖向预应力时可能做到全预应力; 否则主拉应力难以消除, 受力为部分预应力或钢筋混凝土状态。

表1 一个混凝土单箱单室箱梁截面的完整验算应力 Table 1 Complete section checking stress of concrete single cell box girder

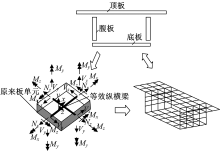
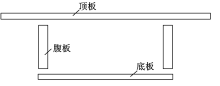
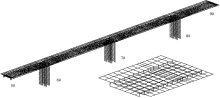
在结构分析中, 可以将复杂的桥梁结构离散成由多块板构成, 再将每一个板元由十字交叉的正交梁格组成, 以十字交叉的纵横梁(6自由度梁单元)的刚度代替板的刚度, 一片正交梁格就像是一张网, 一个结构由多少块板构成, 就可以用梁格表示成多少张网。这样, 空间桥梁结构可以用空间网格来表达。如图1所示, 一个单箱单室箱梁截面可以分解为顶板、底板以及多块腹板构成, 箱形截面梁所离散成的板就可以用正交梁格模型来模拟。由于这些板位于不同的平面内, 代表它们的正交梁格也在不同的平面内(对于弯梁桥为曲面), 不同平面内的正交梁格将箱形截面梁离散为一个空间网状模型, 可以形象地称为空间网格模型^[9]。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 空间网格模型简化原理示意图Fig.1 Schematic diagram of spatial grid model

2.1 板件应力表达方式— — 三层应力

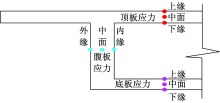
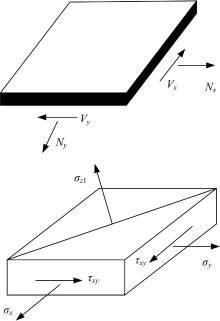
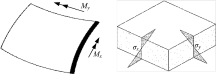
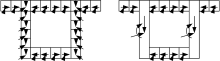
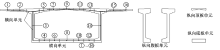
箱梁需要关注的完整的验算应力是实用精细化分析的重要新概念。以图2所示的一个在板厚方向具有相同应力分布的的板式构件组成的单箱单室薄壁箱型截面为例, 来说明表1中的验算应力。表1中箱型截面的应力部位如图3所示, 图中的应力部位与表1的验算应力一一对应。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 由“ 板” 表达的单箱单室箱梁截面Fig.2 Section of single cell box girder expressed by “ plane”

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 验算应力位置示意图Fig.3 Location diagram of checking stress

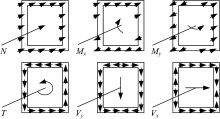
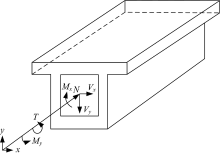
对于一个空间桥梁结构, 其整体受力可以表征为:轴向力N、两个方向的剪力V_x和V_y、两个方向的弯矩M_x和M_y、以及扭矩T共6个力。从应力角度在箱梁断面上对这耦合的6种受力方式进行归并和分解, 如图4、图5所示, 它表达了由外荷载产生的整体效应^[8]。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 外荷载的整体效应Fig.4 Global effect of external load

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 薄壁箱梁中面的面内应力Fig.5 In-plane stress of box girder

其中, 轴向力和弯矩产生的是正应力, 而剪力和扭矩产生的是剪应力, 这些应力是可以相互叠加的。于是, 最终在截面的各个组件(顶板、底板和腹板)各点的受力均只有正应力和剪应力, 这样就将6种受力归并为两种应力了, 而正应力和剪应力又可以合成为主应力。所以, 归根到底, 结构的受力均可以用主应力来衡量, 正应力只是主应力的一种特殊情况(剪应力为0)^[9]。对应产生的中面应力是二维薄壁应力, 如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 板中面的薄壁应力Fig.6 Thin wall stress of middle plane

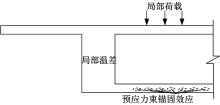
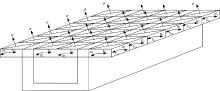
每块板的上下缘面外应力表达了局部荷载产生的局部效应, 是一维应力, 如桥面板计算中的车轮荷载, 以及变高度箱梁的底板纵向预应力钢束产生的外崩力, 如图7、图8所示。每块板件在局部荷载作用下的变形和应力分布如图9所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 外荷载的局部效应Fig.7 Local effect of external load

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 箱梁各板件上下缘面外应力Fig.8 Upper and lower out-plane stress of box girder

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 薄壁箱梁面外效应变形及应力示意图Fig.9 Deflection and stress diagram of box girder out-of-plane

2.2 单梁转化为空间网格模型概述

6自由度单梁的整体受力特征表现为6个力:轴力N、两个方向的剪力V_x和V_y、两个方向的弯矩M_x和M_y以及扭矩T, 如图10所示。混凝土箱梁结构顶底板、腹板上应力分3层, 顶底板分上缘、中面、下缘, 腹板分外缘、中面、内缘, 如图3所示。对于单梁, 整体效应在截面上产生应力(正应力、剪应力)的位置是顶底板、腹板中面, 如图5所示, 图5中板内仅有正应力和剪应力, 其中轴向力和弯矩产生正应力, 而剪力和扭矩产生的是剪应力, 这些应力是可以相互叠加的。这样就将6种受力归并为两种应力了, 而正应力和剪应力又可以合成为主应力。故最终结构的受力均可以用主应力来衡量, 纯弯和纯剪分别只产生的正应力和剪应力仅是主应力的一种特殊情况^[9], 图6表达了箱梁任意板内受力及主应力表达方式。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 外荷载在截面上的整体效应Fig.10 Section global effect of external load

将箱梁划分成空间网格, 整体效应(6种力)分散到整个截面的各个小网格中, 内力及主应力的表达分别如图11、图12所示。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 箱梁网格化后内力表达示意图Fig.11 Internal force diagram of grid box girder

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 箱梁网格化后主应力表达示意图Fig.12 Main stress diagram of grid box girder

某桥跨径布置(63+110+110+63)m, 为预应力混凝土箱型连续刚构桥。针对检测报告中描述的主要病害, 为了分析裂缝产生原因, 并为加固作出可靠依据, 利用空间6自由度空间网格模型对已有桥梁结构进行受力状态分析。

全桥模型如图13所示, 计算模型由空间6自由度梁格系组成, 全桥共分4762个节点和8610个单元。横隔梁在模型计算时只计入结构, 重力按均布荷载计入。主桥支座采用带铰单元模拟, 下部节点按实际约束进行设置, 上部节点设为带铰单元的铰接点。成桥约束布置如图14所示。桥梁整体坐标系的选取为:原点设在一侧端横梁的中点, 方向规定根据右手规则, x方向沿桥梁纵向, y方向为竖直向上, z方向沿桥梁横向。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 连续刚构空间网格模型Fig.13 Space grid model of continuous rigid frame

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 约束布置方式Fig.14 Bearing restraint arrangement

箱梁断面的划分和节点分布情况, 如图15所示, 沿纵向共分为16根纵梁:直腹板划分为1根工字型纵梁单元, 可以得到截面上、下缘位置的正应力及腹板上、中、下3个位置的主应力; 顶、底板划分为多个板单元, 可以得出板单元上、下缘的正应力及单元的面内主应力。

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 网格截面划分Fig.15 Division of cross section in spatial grid model

主桥存在诸多裂缝, 其中主要是腹板纵、横方向及网状裂缝。通过空间分析计算活载效应、温度效应、基础变位等, 包括模拟整个悬臂施工过程, 查看出现问题区域的应力分布以寻求裂缝出现的原因, 根据病害成因, 布置体外束进行加固, 并对加固效果进行分析, 以期验证空间网格模型分析体外束加固连续刚构桥的精确性与合理性。以往体外束加固桥梁仅针对正应力, 忽略了主应力。本文不仅关注正应力而且关注主应力, 达到对应力全面加固的目的^{[6, 10]}。

根据裂缝出现情况及空间网格模型试算结果, 对比出最好的体外束布置方案, 如图16所示。

图16

Fig.16

	Figure Option ViewDownloadNew Window
	图16 加固方案示意图Fig.16 Schematic diagram of reinforcement scheme

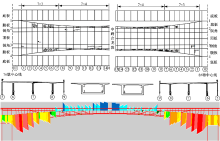
为了验证空间网格模型的应力分析效果, 本节将加固前原结构的应力分布结果与实际裂缝分布进行比较。图17~图21为边中跨裂缝分布与拉压应力分布对应图。从对比图结果来看, 拉应力超限区域与裂缝分布区域基本一致, 裂缝主要发生在腹板。由此可知, 采用精细化的空间网格模型分析混凝土连续刚构桥的开裂与应力分布是较全面和准确的, 图17中左右腹板的应力分布基本一致, 因此只列出一侧应力分布图。

图17

Fig.17

	Figure Option ViewDownloadNew Window
	图17 全桥开裂状态拉压应力分布图Fig.17 Tension and compression srtess distribution diagram of full bridge crack

图18

Fig.18

	Figure Option ViewDownloadNew Window
	图18 第1跨裂缝与应力分布对比图Fig.18 Comparison of fracture and stress distribution in the first span

图19

Fig.19

	Figure Option ViewDownloadNew Window
	图19 第2跨裂缝与应力分布对比图Fig.19 Comparison of fracture and stress distribution in the second span

图20

Fig.20

	Figure Option ViewDownloadNew Window
	图20 第3跨裂缝与应力分布对比图Fig.20 Comparison of fracture and stress distribution in the third span

图21

Fig.21

	Figure Option ViewDownloadNew Window
	图21 第4跨裂缝与应力分布对比图Fig.21 Comparison of fracture and stress distribution in the fourth span

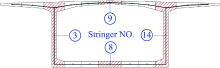
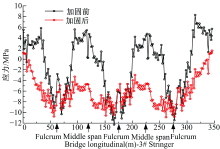
根据弯矩图的趋势布置体外索, 转向块在索形变化处设置^{[6, 10]}。计算模型中将体外索视为独立于结构的单独杆件, 在体外索转向处与梁之间加一根刚臂, 刚臂与梁单元连接处设置橡胶元, 用以调整体外索与转向器之间的摩擦因数。截面划分了16道纵梁, 选取4道关键的纵梁进行对比, 从图15可知, 关键纵梁的选取位置如图22所示。

图22

Fig.22

	Figure Option ViewDownloadNew Window
	图22 关键纵梁选取位置Fig.22 Key stringer location

正常使用阶段下, 加固前后, 关键纵梁③、⑧、⑨及 的正应力(受拉情况)和截面中层主拉应力效果对比图, 分别如图23~图30所示。

图23

Fig.23

	Figure Option ViewDownloadNew Window
	图23 加固前后纵梁③正应力对比Fig.23 Comparison of normal stress of beam ③ before and after reinforcement

图24

Fig.24

	Figure Option ViewDownloadNew Window
	图24 加固前后纵梁③面内主拉应力对比Fig.24 Comparison of principal tensile stress in-plane of beam ③ before and after reinforcement

图25

Fig.25

	Figure Option ViewDownloadNew Window
	图25 加固前后纵梁⑧正应力对比Fig.25 Comparison of normal stress of beam ⑧ before and after reinforcement

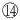
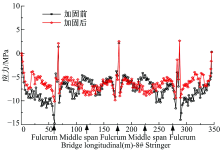
通过对加固前后关键纵梁(③、⑧、⑨、 )的正应力和面内主拉应力比较可知, 加固后, 纵梁③为左侧腹板, 边跨和中跨正应力降低的最多, 基本上由受拉转为受压, 降低幅度为1.25~8倍, 3个中支点区域正应力略有降低, 基本是维持全受压

图26

Fig.26

	Figure Option ViewDownloadNew Window
	图26 加固前后纵梁⑧面内主拉应力对比Fig.26 Comparison of principal tensile stress in-plane of beam ⑧ before and after reinforcement

状态, 支点区域的正应力降低幅度为22%~57%; 纵梁③的面内主拉应力在全跨范围内均大幅度减小, 尤其是边跨和中跨区域, 降低幅度为0.66~8.79倍, 中跨区域的主拉应力变为主压应力, 支点区域降低幅度为0.44~1.54倍, 均变为主压状态。

图27

Fig.27

	Figure Option ViewDownloadNew Window
	图27 加固前后纵梁⑨正应力对比Fig.27 Comparison of normal stress of beam ⑨ before and after reinforcement

图28

Fig.28

	Figure Option ViewDownloadNew Window
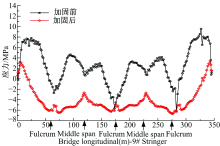
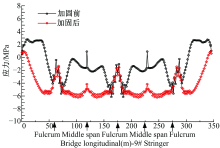	图28 加固前后纵梁⑨面内主拉应力对比Fig.28 Comparison of principal tensile stress in-plane of beam ⑨ before and after reinforcement

纵梁⑧位于底板跨中, 在全跨范围内, 正应力有所改善, 除了支点有一个点跳跃外, 其余位置均为压应力, 全跨范围内的正应力降低幅度为8%~87%; 纵梁⑧的面内主拉应力在全跨范围内均大幅度减小, 除中跨跨中区域个别点仍存在很小的主拉应力外, 其余位置均为主压应力状态, 降低幅度为0.14~6.15倍。

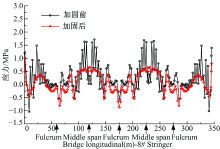
纵梁⑨位于顶板跨中, 在全跨范围内, 加固后正应力均大幅度降低, 基本全变成压应力, 全跨范围内的正应力降低幅度为0.25~8.52倍; 纵梁⑨的面内主拉应力在全跨范围内均大幅度减小, 除支点区域有轻度改善外, 其余位置改善较大且均为主压应力状态, 降低幅度为0.17~6.62倍。

图29

Fig.29

	Figure Option ViewDownloadNew Window
	图29 加固前后纵梁 正应力对比Fig.29 Comparison of normal stress of beam before and after reinforcement

图30

Fig.30

	Figure Option ViewDownloadNew Window
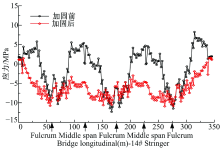
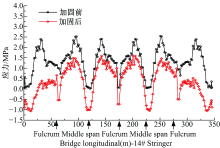	图30 加固前后纵梁 面内主拉应力对比Fig.30 Comparison of principal tensile stress in-plane of beam before and after reinforcement

纵梁 为右侧腹板, 纵梁的边跨和中跨正应力降低的最多, 基本上由受拉转为受压, 降低幅度为0.15~6.19倍, 3个中支点区域正应力略有降低, 基本是维持全受压状态, 支点区域的正应力降低幅度为10%~54%; 纵梁 的面内主拉应力在边跨和中跨跨中区域有大幅度减小, 其余区域也有不同程度的减小, 降低幅度为0.19~8.39倍。

从正应力和面内主拉应力角度来看, 加固前后, 每道纵梁的受力状态均得到改善。面内主拉应力是正应力和剪应力的合成, 对面内主应力进行主动加固, 更能体现出加固效果。单一地比较正应力的加固效果, 不能完全反应加固后梁体受力的改善状态。

(1)空间网格模型分析的完整性应用在体外束加固连续刚构桥的受力分析中, 可以看出其优势在于:①完全考虑施工过程(徐变收缩、预应力); ②空间影响面加载, 从而解决横向受力和腹板受力分配; ③完全反映完整验算应力, 特别是桥面板和底板的面内主拉应力。

(2)以加固结构正应力和面内主拉应力的角度来看, 在正常使用阶段, 加固前后, 每道纵梁的受力状态均得到改善。面内主拉应力是正应力和剪应力的合成, 对面内主应力进行主动加固, 更能体现出加固效果。单一地比较正应力的加固效果, 不能完全反应加固后梁体受力的改善状态。

(3)体外预应力是桥梁加固的一种有效方法, 从分析结果来看, 体外束对腹板加固效果尤为明显, 但对上、下翼缘的影响有限, 所以应该采取一些措施来提高预应力对翼缘板的影响。