作者简介:尼颖升(1984-),男,助理研究员,博士. 研究方向:桥梁加固及波形钢腹板组合梁.E-mail:ys.ni@rioh.cn
针对波形钢腹板组合箱梁配筋方法的不足,提出了基于空间网格分析方法和“拉应力域”的设计方法。结合工程案例,将网格配筋、设计配筋及规范配筋结果进行了对比并描述了截面关键板件纵向配筋趋势。结果表明:基于拉应力域的配筋计算方法可以实现波形钢腹板组合梁桥顶板和底板的面内、面外精细化配筋,验证了网格模型模拟波形钢腹板组合箱梁的准确性。空间网格模型和拉应力域设计方法可为波形钢腹板组合箱梁提供精细化的设计思路和方向。
To overcome the shortcomings of the design method of composite box girder corrugated steel webs, a spatial grid analysis model and a design method based on “tensile stress region” are proposed. Taking engineering cases, the mesh reinforcement, design reinforcement and standard reinforcement results are compared, and the longitudinal reinforcement trend of key slab in the cross section is described. The results show that the calculation method of reinforcement based on “tensile stress region” can realize the fine reinforcement of in-plane and out-of-plane in the top and bottom plane of the composite beam bridge with corrugated steel web, and verify the accuracy of the grid model in simulating the composite box girder with corrugated steel web. So the spatial grid model and “tensile stress region” design method can provide references to fine design of composite box girder corrugate steel web.
波形钢腹板组合梁桥结构形式从最初的简支梁、连续梁发展到现在的连续刚构、斜拉桥, 截面形式也从单箱单室应用到单箱多室及多箱多室。日本是波形钢腹板组合梁应用和建造最多的国家, 其已建造的波形钢腹板组合梁达200余座, 中国已建和在建的波形钢腹板桥近30座。以河北邢台白泉大道的郭守敬桥和钢铁路桥(国内第1座一箱七室波形钢腹板组合箱梁桥)、山东鄄城黄河大桥((70+11× 120+70)m波形钢腹板预应力混凝土连续箱梁)及在建的江西南昌朝阳大桥((60+5× 120+60)m波形钢腹板斜拉桥)等4座桥最为典型[1, 2, 3, 4]。
目前, 波形钢腹板组合梁桥的设计及配筋是参照日本《波形钢腹板预应力混凝土桥设计、施工规范》、广东省地方标准— — 《波形钢腹板预应力混凝土箱梁桥技术规程》、河南省地方标准— — 《公路波形钢腹板预应力混凝土箱梁桥技术规范》等[5], 中国尚没有统一的设计规范, 因此顶底板的设计配筋依然采用桥规中单一的截面法。设计中通常采用空间杆系模型、平面梁格法与局部实体分析相结合的分析方法[6]。但是, 空间杆系模型缺乏对空间效应的精细化分析, 比如:宽箱梁的平截面假定、有效分布宽度、偏载系数、各个腹板的内力分配、横向分布系数等问题; 平面梁格法由于采用等效原理, 不能准确反映箱形组合梁的剪应力分布和顶底板局部受力; 实体分析很难与总体计算完全结合, 分析结果是总体应力结果, 与现行规范中的内力配筋设计方法不匹配, 往往只在局部分析中应用[7]。
同时在验算应力方面, 对于一个复杂桥梁, 结构在外荷载作用下的受力效应不能再简单地以分别代表顶板上缘和底板下缘的“ 截面上、下缘应力” 作为表示验算应力, 而是每一个组成板件(顶板、底板和腹板)的上缘、下缘和面内主应力都需要关注, 从而可以用对应的验算应力来反映该位置的受力情况及可能发生的开裂情况, 这样能更精确地反映该桥结构的复杂受力情况[8, 9]。
因此, 针对波形钢腹板PC箱梁桥, 有必要通过计算手段的改进来确定一种新的结构分析方法, 重新对其进行内力和应力分析, 有针对性地提出新的配筋方法。鉴于此, 文献[8, 9]讲述并应用了实用精细化分析方法— — 空间网格模型, “ 拉应力域” 是以空间网格模型为平台来实现板件的精细化计算与配筋。网格模型将组合梁截面视为由若干块板组成, 对每一块板进行梁格划分, 用划分后的梁格等效代替每块板的受力。相比梁格法, 空间网格划分得更细。由于将顶板划分得更密, 可以分析出顶板的各梁格在剪力滞效应下的应力, 且不用计算有效宽度。刚性扭转通过空间网格之间的相互作用反映在各个梁格的剪应力上, 同样可以实现在荷载作用下截面的畸变分析及截面各个板件的横向弯曲变形。它能够分析组合梁截面在偏心荷载作用下的各种变形形态。空间网格模型输出的结果是各个梁格的内力、应力及位移, 可以方便得到结构不同部位的受力状态, 从而有针对性地加强构造配筋, 对实际工程的设计分析有重要意义。
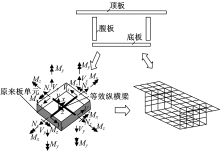
在结构分析中, 可以将复杂的桥梁结构离散成由多块板构成, 再将每一个板元由十字交叉的正交梁格组成, 以十字交叉的纵横梁(6自由度梁单元)的刚度等代成板的刚度, 一片正交梁格就像是一张“ 网” , 一个结构由多少块板构成, 就可以用梁表示成多少张“ 网” 。这样, 空间桥梁结构可以用空间网格来表达。如图1所示, 一个单箱单室箱梁截面可以分解为顶板、底板以及多块腹板构成, 箱形截面梁所离散成的“ 板” 就可以用正交梁格模型来模拟。由于这些“ 板” 位于不同的平面内,
代表它们的正交梁格也在不同的平面内(对于弯梁桥为曲面), 不同平面内的正交梁格将箱形截面梁离散为一个空间“ 网” 状模型, 可以形象的称为“ 空间网格” 模型[8]。
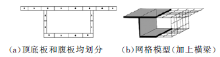
建立空间网格模型时, 纵向依据单梁有限元划分方式划分(即考虑的因素通常为结构受力、自然施工划分等); 截面内部划分的疏密程度根据截面形式和计算要求确定, 它反映了表达空间效应的精细化程度。空间网格模型截面划分时将腹板分块。腹板与顶、底板均划分, 对应的截面划分及网格模型如图2所示
按图2离散后所得的空间网格模型中, 截面主要有以下3种:腹板整体截面, 腹板划分截面, 纵、横向顶底板划分截面, 如图3所示。这些截面及特性计算与传统梁单元截面特性计算一致, 由离散后实际截面尺寸计算[9]。
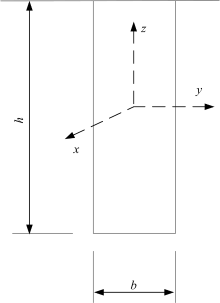
这里以图4所示的矩形截面为例, 说明网格模型中常用截面的截面特性计算方法:
轴向面积为:
Ax=bh(1)
剪切面积为:
Ay=Az=bh(2)
抗弯惯矩为:
Iz=
截面划分后, 划分截面的抗扭惯矩对整体截面的影响相当有限, 故抗扭惯矩可采用如下简化公式计算:
IT=
在空间网格模型中, 截面荷载效应分担如下: ①箱梁截面的纵向效应(如轴力、弯矩)由纵向梁格承受; ②箱梁截面的横向效应(如畸变、活载横向效应等)由横向梁格承受; ③箱梁截面的扭转、畸变效应转化为腹板梁格的剪力。
在空间网格模型中, 通过分析计算可以得到组成网格的各部分截面(腹板整体截面或腹板划分截面)的内力(包括轴力、弯矩、剪力、扭矩), 单元内力按照单元刚度进行分配, 对于不同的截面形式, 荷载效应的计算方式分别如下所述。
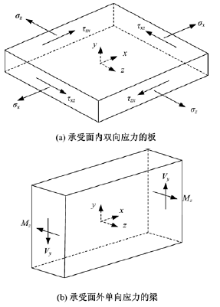
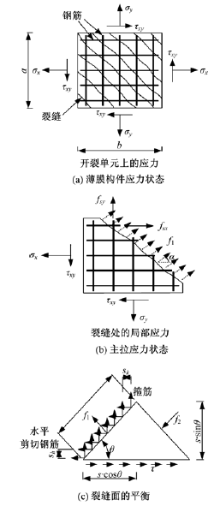
一般用于模拟网格模型中的箱梁顶板和底板, 主要承受轴力Nx、Ny, 面内剪力Vxy以及面外弯矩Mx、My。如图5所示, 沿着单元厚度均匀分布的薄膜效应和顶底板的局部荷载效应可以通过“ 划分截面” 完全体现出来[10, 11, 12, 13, 14, 15]。
(1)面外正应力
σ x=
σ y=
式中:σ x为截面x向正应力; σ y为截面y向正应力; z为计算正应力应力点至截面重心轴的距离, 重心轴以上取正值; Ix、Iy分别为垂直于y轴或x轴的截面绕各自截面重心轴惯性矩; Mx、My分别为垂直于y轴或x轴的截面绕各自截面重心轴弯矩。
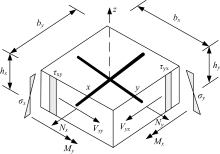 | 图5 空间网格模型“ 划分截面” 效应计算示意图Fig.5 Schematic diagram of “ division section” effect calculation of spatial grid model |
(2)面内正应力
σ x-m=
σ y-m=
式中:σ x-m分别为截面中面x向正应力; σ y-m分别为截面中面y向正应力; bx、by分别为截面中垂直于x向或y向截面的宽度; hx、hy分别为截面中垂直于x向或y向截面的高度。
(3)面内剪应力
τ xy=
(4)面内主拉应力σ t和主压应力σ c:
空间网格模型不仅能够准确分析复杂结构的空间受力状态, 而且其输出的数据结果(以单元杆端力的方式输出)是各个梁格单元的内力、应力及位移, 可以方便得到结构不同部位的受力状态, 并且与现行桥梁设计规范直接对应, 从而有针对性地指导桥梁各部分的配筋设计, 对实际工程的设计分析有重要意义。
空间网格模型中的各块“ 板” 共同作用构成箱形截面梁独特的全截面抗弯、抗扭与抗剪刚度。这些板可以是钢的, 可以是混凝土的, 或其他任意材料的。于是, 这些板元便可以组合成全混凝土截面、全钢截面、部分是钢部分是混凝土的截面(钢 混凝土叠合梁)以及其他任意几种不同材料组成的截面。故空间网格模型适用于弯桥、斜桥、宽桥、组合梁等各种桥型, 不受具体结构形式的限制[16]。
“ 拉应力域” 配筋设计理论首先根据构件受力特点, 对目前桥梁上部结构进行重新划分。将桥梁的内部受力类型分为面内双轴受力的“ 板” 和承受面外弯矩的“ 梁” :前者代表结构的整体效应, 受力方向为面内(见图6(a)); 后者代表结构局部效应, 受力方向为面外(见图6(b))。其中, “ 承受面外单向应力的梁” 是与基于柔细梁的现行规范相衔接的, 适用于现行规范中所有关于纯弯“ 正截面” 设计状态、配筋方法和设计安全度的条款; 因而, 代表结构整体效应的承受面内双向应力的板是“ 拉应力域” 配筋设计方法的唯一原型构件[8]。
对于承受面内双向应力的板, 由于所受的正应力与剪应力沿厚度方向均匀分布, 因而合成为面内主应力时, 主应力也沿板厚方向均匀分布, 即可视这类板处于薄膜应力状态, 并将薄膜板中承受主拉应力的二维应力区域定义为“ 拉应力域” 。
对“ 拉应力域” 区域的钢筋混凝土薄膜板进行分析:当主拉应力小于混凝土抗拉强度时, 主要仍由混凝土承担主拉应力; 当主拉应力超过混凝土抗拉强度时, 混凝土开裂且承担主拉应力的能力大大减弱, 需要配置相应的钢筋来承担引起混凝土开裂的主拉应力, 保证构件能够继续承载。也就是说, 开裂后的钢筋混凝土单元中, 原来由混凝土承担的主拉应力将由钢筋承担[8]。基于这一目标, “ 拉应力域” 筋设计理论提出了一种新颖的剪切钢筋配筋设计理论, 以及剪切钢筋布置方式— — 正交网格剪切钢筋。薄膜构件在外荷载作用下的应力状态如图7(a)所示, 等效主拉应力f1如图7(b)所示, 不计裂缝间混凝土抵抗主拉应力的能力, 该主拉应力在斜裂缝出现后完全由正交分布的钢筋承担, 因此建立平衡体系使得结构单元继续承担外荷载, 如图7(c)所示。微元体裂缝长度为s, 混凝土主压应力倾角为θ , 在裂缝面上通过配置正交各向同性的水平钢筋和竖向钢筋分别平衡开裂后主拉应力的水平分量及竖直分量, 相应的平衡方程为:
f1× s× b× cosθ =fsv× Asv×
f1× s× b× sinθ =fsh× Ash×
简化上述算式后, 得到水平钢筋及竖向钢筋的配筋率分别为:
式中:Asv、Ash分别为竖向箍筋和水平钢筋的面积; sk、sh分别为竖向箍筋和水平钢筋的间距; fsv、fsh分别为竖向箍筋和水平钢筋的屈服应力; f1为混凝土“ 转给” 钢筋的主拉应力。
网格模型下波形钢腹板的承载力配筋方法总体是基于“ 拉应力域” 配筋的方式, 配筋分为面内纵横向配筋和面外纵横向配筋, 求出顶、底板每小块板配筋量, 将网格配筋与单梁配筋进行比较。可通过图示和表格的方式表达上述过程, 网格配筋过程如图8所示。
郑州陇海路主线高架桥梁上部结构为波形钢腹板混凝土箱梁结构, 跨径孔布置为31 m+(9× 50) m+(9× 50+40) m +(3× 26) m+(52+80+52) m +(32.061+32+31.876) m左幅/(34.906+34.98+35.09) m右幅, 其中(9× 50) m+(9× 50+40) m为波形钢腹板连续组合箱梁, 本案例采用(9× 50) m一联进行分析, 该桥跨径布置如图9所示。
计算模型由空间6自由度梁格系组成, 全桥共分5625个节点和12009个单元。横隔梁在模型计算时只计入结构, 重力按均布荷载计入, 体外预应力钢束用只受轴向力的杆件模拟。网格模型中, 主桥支座采用支座连杆单元模拟, 上部节点连接到支座横梁竖杆单元下节点上, 全桥支座连杆的下节点按计算工况(施工过程或成桥状态)进行约束。桥梁整体坐标系的选取为:原点设在一侧端横梁的中点, 方向规定根据右手规则, x方向沿桥梁纵向, y方向为竖直向上, z方向沿桥梁横向。
需要对波纹钢腹板纵向弹性模量E0进行修正, 采用有效弹性模量Ex的方式。此结构的波形钢腹板有厚度t=16 mm和t=20 mm两种类型。当t=16 mm时, Ex/E0≈ 500; 当t=20 mm(仅两边跨端部支点搭接段采用, 长度为4.65 m)时, Ex/E0≈ 320.1。在空间网格模型中, 修改代表波纹钢腹板的纵向单元纵向刚度, 按照理论公式计算的折减倍数, 在厚度t=16 mm和t=20 mm处将钢腹板纵杆单元轴向刚度面积折减500倍和320.1倍, 其余几何特性及材料参数等不进行修正, 陇海路高架的空间网格计算模型如图10所示。
为表达“ 拉应力域” 配筋的设计效果, 此次配筋选取内力较大的边跨0.5 L、边跨中支点的横截面及图10(c)中2#、3#、7#、8#关键板件纵向实施。将网格配筋结果与规范的单梁配筋、已完成的设计图纸进行对比, 以此来说明基于“ 拉应力域” 波形钢腹板组合箱梁承载力配筋的经济性和有效性。
(1)横截面配筋
空间网格模型将顶底板分为面内和面外配筋, 此模型已经考虑桥面板横向效应, 不用单独计算桥面板配筋; 单梁仅仅是面外的纵向整体配筋, 仅配受拉区钢筋。图11~图14分别表示了边跨0.5 L网格、设计图纸及单梁的配筋及腹板应力对比结果; 图15~图18分别表示了边跨中支点网格、设计图纸及单梁的配筋及腹板应力对比结果。
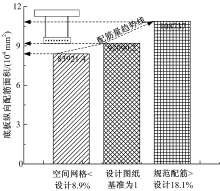
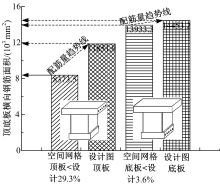
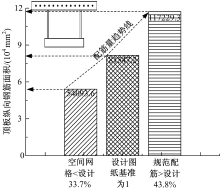
通过图11可知, 空间网格的应力配筋量小于设计图纸20%, 规范单梁配筋量大于设计图纸12.1%, 空间网格的配筋量小于规范单梁配筋量将近30%。通过图12可知, 空间网格的应力配筋量小于设计图纸8.9%, 规范单梁配筋量大于设计图纸18.1%, 空间网格的配筋量小于规范单梁配筋量近26%。通过图13可知, 顶板横向空间网格的应力配筋量小于设计图纸29.3%, 底板横向空间网格的应力配筋量小于设计图纸3.6%。
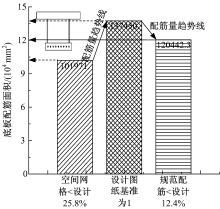
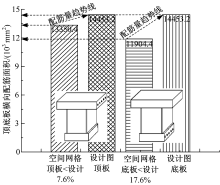
通过图15可知, 空间网格的应力配筋量小于设计图纸33.7%, 规范单梁配筋量大于设计图纸43.8%, 空间网格的配筋量小于规范单梁配筋量将近70%。通过图16可知, 空间网格的应力配筋量小于设计图纸25.8%, 规范单梁配筋量小于设计图纸12.4%, 空间网格的配筋量小于规范单梁配筋量近13%, 网格配筋量最小。通过图17可知, 顶板横向空间网格的应力配筋量小于设计图纸7.6%, 底板横向空间网格的应力配筋量小于设计图纸17.6%。
单梁模型无法计算出桥面板的横向钢筋, 必须借助于空间有限元程序完成。空间网格配置顶底板纵横向钢筋量均小于设计图纸和规范单梁的配筋量, 规范单梁的配筋量普遍偏大。但是基于应力的配筋, 考虑配筋的项目比较全面、计算的比较清楚且所配钢筋均为受力钢筋。
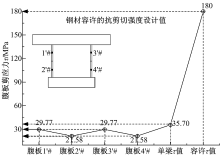
通过图14和图18中腹板的应力图对比结果来看, 沿腹板高度方向, 空间网格模型可以提取不同点的应剪应力值, 表示了钢腹板剪应力高度方向分布趋势, 单梁计算结果为一个平均剪应力值, 量值略大于空间网格模型计算结果, 但两种计算结果均小于钢材的抗剪强度设计值。
(2)网格关键板件纵向配筋趋势、
板块2#、3#、7#及8#是箱梁截面关键位置, 通过面内、面外配筋, 沿全跨范围内绘制成配筋趋势线, 板块2#、3#、7#及8#的配筋趋势线如图19所示。
截面上2#、3#板块位于顶板, 7#、8#板块位于底板, 由图19可知, 2#与3#板块配筋量突变处位于各个支点负弯矩区, 7#与8#板块配筋量突变处位于各跨跨中区, 2#、3#、7#、8#板块的配筋趋势线与连续梁支点负弯矩、跨中正弯矩的弯矩图基本一致。
实桥设计配筋应用时, 顶板或底板的配筋参考全跨范围内配筋趋势线, 依据节段配筋量的大小进行粱跨间节段配筋; 也可以根据全跨范围内配筋趋势线, 取最大值于全跨范围内通长布置, 这样施工具有便利性。
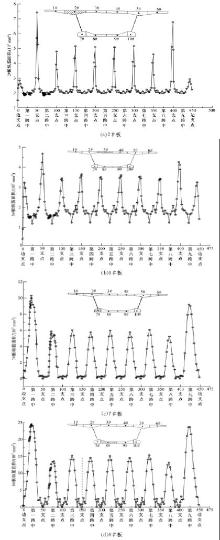 | 图19 2#, 3#, 7#和8#板于全跨范围内纵向配筋趋势线Fig.19 Longitudinal reinforcement trend line across span of 2#, 3#, 7# and 8# slab |
在研究阶段, 通常认为设计图纸和规范单梁所配钢筋布置在板件的上、下缘, 而空间网格面内所配十字交叉钢筋理想的位置是在板件中面, 面外所配纵、横向钢筋根据外力的方向来确定是布置在板件的上缘还是下缘, 除了受力钢筋配置要求外, 还要符合公路桥规关于顶底板配筋的构造规定。
从全跨范围内整体配筋趋势线来看, 各个截面、各个节段的配筋量表达的比较清楚, 说明空间网格模型对(9× 50) m波形钢腹板连续组合箱梁整体配筋具有适用性。
通过对一联(9× 50) m等高度的波形钢腹板预应力混凝土组合连续箱梁桥的配筋比较可知, 对于顶底板的纵向配筋, 规范配筋量偏大于网格配筋或设计图纸配筋, 其中空间网格配筋量最小, 总体上是规范单梁配筋量大于空间网格配筋量; 对于顶底板的横向配筋, 单梁模型无法计算出桥面板的横向钢筋, 需借助于空间有限元程序完成, 设计图纸中顶底板的横向钢筋配筋量均大于网格配筋配筋量。由此得出以下结论:①提出了基于“ 拉应力域” 的波形钢腹板组合箱梁配筋计算方法, 实现了波形钢腹板组合梁桥顶板和底板的面内、面外精细化配筋; ②提出的波形钢腹板组合箱梁的空间网格模型与实体模型的比较结果验证了网格模型模拟波形钢腹板组合箱梁的准确性; ③空间网格模型和“ 拉应力域” 设计方法可为波形钢腹板组合箱梁提供精细化的设计。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|