车用双电源开绕组电机驱动系统绕组模式切换及电流控制策略

引用本文

贾一帆, 初亮, 许楠, 徐哲. 车用双电源开绕组电机驱动系统绕组模式切换及电流控制策略[J].吉林大学学报（工学版）, 2018,48(1): 20-29
JIA Yi-Fan, CHU Liang, XU Nan, XU Zhe. Winding mode shifting and current control strategy of dual power open-winding PMSM drive system for electric vehicle[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 20-29 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170057
Permissions

车用双电源开绕组电机驱动系统绕组模式切换及电流控制策略

贾一帆¹, 初亮¹, 许楠¹, 徐哲²

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.中国第一汽车股份有限公司技术中心,长春 130011

通讯作者：许楠(1984-),男,讲师,博士.研究方向:新能源车辆驱动理论及控制.E-mail:nanxu@jlu.edu.cn

作者简介:贾一帆(1992-),男,博士研究生.研究方向:电动汽车驱动理论及控制.E-mail:695424875@qq.com

基金:中国博士后科学基金项目(2014M561290); 吉林省青年科研基金项目(20150520115JH); 长春市科技计划项目(14KG098)

摘要

针对电动车用双电源双逆变器开绕组永磁同步电机驱动系统,提出星形、角形、独立3种绕组模式及实现方法。在分析各模式电机外特性的基础上,制定了绕组模式切换策略,其中的转矩饱和判定算法可实现对电机参数变化不敏感的绕组模式自动向上切换。同时提出了用于独立模式的多电平电流滞环调制算法,增加了电平数量及触发机制,可指定主电源并实时切换,从而实现两电源间的能量分配;其具有低开关频率和大功率差值两种控制方式,可达到不同的节能与能量分配效果。仿真结果表明:本文方法充分利用了各绕组模式的工作区间,减少了器件损耗并提高了系统效率,为双电源构型下车用动力系统的建立提供了理论依据与工程方案。

关键词: 车辆工程; 开绕组永磁同步电机; 绕组模式切换; 转矩饱和判定; 电流滞环调制; 能量分配

中图分类号:TM351 文献标志码:A 文章编号:1671-5497(2018)01-0020-10

Winding mode shifting and current control strategy of dual power open-winding PMSM drive system for electric vehicle

JIA Yi-Fan¹, CHU Liang¹, XU Nan¹, XU Zhe²

1.State Key Laboratory of Automotive Simulation and Control,Jilin University,Changchun 130022,China

2.R&D Center,China FAW Group Corporation,Changchun 130011,China

Abstract

Aiming at dual power Open-winding Permanent Synchronous Motor (OW-PMSM) for electric vehicle, three winding modes, star mode, triangle mode and independent mode, and their implementation methods were proposed. A novel winding mode shifting strategy was put forward on the basis of discussing the working range of each winding mode, in which the torque saturation decision is insensitive to motor parameters. Also a multi-level current hysterisis modulation method was proposed, which could assign the main power source and change it anytime by additional electric levels and their trigger mechanism. Using this method the energy can be distributed between two power sources. The modulation method has two patterns, the low switching frequency pattern and the high power difference pattern, to achieve different energy distribution effects. Simulation results show that, the proposed method can take full advantage of the working range of each winding mode, reduce device loss and improve the effectiveness of the system, and provide theoretical basis and engineering proposal for designing the drive system of electric vehicle with dual power sources.

Keyword: vehicle engineering; open-winding permanent magnet synchronous motor; winding mode shift; torque saturation decision; current hysterisis modulation; energy distribution

Show Figures

0 引言

随着当今社会对节能环保要求的提高, 以电动机为动力源的电动汽车技术领域蓬勃发展, 永磁同步电机具有功率密度高、控制简单等优点, 成为电动汽车的常用动力源。近年来开绕组永磁同步电机(OW-PMSM)^{[1, 2]}及其与双逆变器组成的驱动系统^{[3, 4]}获得了广泛的应用。该系统通过在开绕组电机定子绕组两端各连接一个逆变器进行驱动, 相比传统永磁同步电机驱动系统扩展了调速范围并可采用更灵活的控制方法^{[5, 6]}; 并允许两个逆变器从不同电源取电, 双电源场合应用时在省去DC/DC变换器的同时可实现电源间的能量分配^{[7, 8, 9, 10]}。

开绕组永磁同步电机双逆变器的控制一直是研究热点。针对电流控制方法, 文献[3]提出一种双逆变器SVPWM调制, 在电压矢量的中六边形上进行矢量合成, 可将电机基速扩展至星接绕组的1.7倍且不产生零序电压; 文献[5, 6]分别研究了共直流母线结构下双逆变器的SVPWM调制策略, 在最大化电压矢量幅值的同时抑制了零序电流产生; 文献[7]研究了双电源构型下双逆变器电压矢量分配问题, 提出3种电压分配方式以适应不同需求。以上研究均提出了双逆变器电流控制方法, 但未涉及绕组模式的划分与切换。文献[1]研究了五相开绕组电机的绕组模式, 将其分为星形、角形和五角星形并分析了各绕组模式下的电机外特性; 但未研究提出绕组模式切换方法与双电源之间能量分配的问题。

本文首先, 分析三相开绕组永磁同步电机绕组模式的划分和各模式下电机的外特性, 在此基础上提出对参数不敏感的基于转矩饱和判定的模式切换策略, 从而实现电机绕组模式根据工况的自动切换。然后, 提出用于独立模式的多电平电流滞环调制算法, 可以指定主供电电源并实时切换, 实现两个电源之间的能量分配; 并提出低开关频率和大功率差值两种控制方式, 实现不同的能量分配效果。最后, 仿真验证所提绕组模式切换策略和多电平电流滞环控制的可行性和有效性。需要指出, 本文所用定子三相与转子两相之间的坐标变换均为等功率变换。

1 各绕组模式的特性分析与切换策略

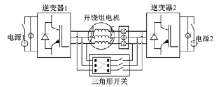
双电源开绕组电机驱动系统基本结构见图1。

	Figure Option View Download New Window
	图1 开绕组电机驱动系统电路结构图Fig.1 Structure of OW-PMSM drive system

三相开绕组永磁同步电机按照绕组连接方式可分为3种绕组模式, 即星形、角形与独立模式。星形模式需将三相定子绕组的始端或末端连接为一点, 在本构型中可通过一侧逆变器每相桥臂下管全部打开实现; 角形模式需将三相定子绕组首尾相连, 可通过关断一侧电源并打开附加的三角形开关实现。独立模式是开绕组电机特有的模式, 每相绕组直接与两侧逆变器的对应桥臂相连, 由两侧的逆变器桥臂协同控制, 绕组间不存在直接的连接关系, 故称为“ 独立” ; 该模式需要两侧电源都提供电压, 同时可以通过电机绕组实现电源之间的能量流动。

1.1 各绕组模式的特性分析

首先讨论电源电压对各绕组模式的限制。不同绕组模式下每相绕组能够获得的最大相电压幅值不同, 各相之间的连接关系也不同, 从而导致基本电压矢量幅值不同。星形或独立模式时, 因负载中性点或中点电位差是浮动的, 相电压并不能根据该相对应的逆变器桥臂开关状态唯一确定, 而会受到其他相的影响。于是使用图2所示的中点电压进行分析; 将电源1和电源2分别按电压对半分成两个部分, 得到虚拟的电压中点m和n, 逆变器每相桥臂的输出端与对应电源中点间电压即为中点电压。中点电压不受浮动的负载中性点或中点电位差影响; 每相桥臂开关状态与中点电压一一对应。用中点电压进行电压矢量合成与使用相电压合成结果相同。

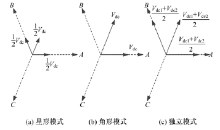
	Figure Option View Download New Window
	图2 中点电压示意图Fig.2 Schematic diagram of mid-point voltage

星形和角形模式由单一电源供电, 逆变器三相桥臂给出开关组合, 可以在电机空间平面上形成特定的电压矢量。设直流母线电压为V_dc, 当逆变器开关组合为(110)时, 星形和角形模式的电压矢量合成图分别如图3(a)、(b)所示。独立模式由两个电源供电和双逆变器控制; 设电源1电压为V_dc1, 电源2电压为V_dc2, 逆变器开关组合为左(110)右(001)时独立模式的电压矢量合成图如图3(c)所示。

	Figure Option View Download New Window
	图3 各绕组模式电压矢量合成图Fig.3 Voltage vector composing of each winding mode

合成后星形、角形与独立模式基本电压矢量幅值分别为 $\begin{matrix} \sqrt[]{\frac{2}{3}} \end{matrix}$ V_dc、 $\begin{matrix} \sqrt[]{\frac{2}{3}} \end{matrix}$ × $\begin{matrix} \sqrt[]{3} \end{matrix}$ V_dc、 $\begin{matrix} \sqrt[]{\frac{2}{3}} \end{matrix}$ (V_dc1+V_dc2)。其中, $\begin{matrix} \sqrt[]{\frac{2}{3}} \end{matrix}$ 是等功率变换系数。可见, 当母线电压为V_dc时, 角形模式的基本电压矢量幅值是星形模式的 $\begin{matrix} \sqrt[]{3} \end{matrix}$ 倍; 独立模式下若有V_dc1=V_dc2=V_dc, 基本电压矢量幅值是星形模式的2倍, 是角形的2/ $\begin{matrix} \sqrt[]{3} \end{matrix}$ 倍。任意方向线性的电压矢量幅值范围应为上述基本电压矢量组成六边形的内切圆半径, 即基本电压矢量幅值的 $\begin{matrix} \sqrt[]{3} \end{matrix}$ /2倍。于是星形、角形、独立模式下任意方向下可用的电压矢量最大幅值u_smax_Y、u_smaxΔ、u_smax_D分别为 $\begin{matrix} \sqrt[]{2} \end{matrix}$ V_dc/2、 $\begin{matrix} \sqrt[]{6} \end{matrix}$ V_dc/2、 $\begin{matrix} \sqrt[]{2} \end{matrix}$ (V_dc1+V_dc2)/2。

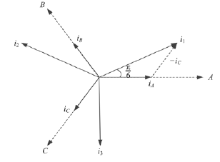
然后讨论定子电流对各绕组模式的限制。由于电机绕组具有电感特性, 所以相电流具有惯性, 不能像相电压一样突变。稳态时, 三相电流在时域上为幅值相等、相位互差2π /3的正弦波; 空间合成后定子电流矢量幅值变为每相电流幅值的 $\begin{matrix} \sqrt[]{\frac{3}{2}} \end{matrix}$ 倍。

在星形和独立模式下, 逆变器器件的电流容量i_max即为相电流最大值。在角形模式下, 线电流i₁、i₂、i₃与相电流i_A、i_B、i_C满足如下关系:

i₁=i_A-i_C, i₂=i_B-i_A, i₃=i_C-i_B(1)

稳态时, 线电流与相电流的时域向量图见图4。可见, 角形模式线电流的幅值是相电流的 $\begin{matrix} \sqrt[]{3} \end{matrix}$ 倍。于是, 当逆变器的电流容量为i_max时, 角形模式相电流最大值为i_max/ $\begin{matrix} \sqrt[]{3} \end{matrix}$ , 合成后定子电流矢量最大幅值也为星形和独立模式的1/ $\begin{matrix} \sqrt[]{3} \end{matrix}$ 倍。星形、角形和独立模式的电流矢量最大幅值i_smax_Y、i_smaxΔ、i_smax_D分别为 $\begin{matrix} \sqrt[]{6} \end{matrix}$ i_max/2、 $\begin{matrix} \sqrt[]{2} \end{matrix}$ i_max/2、 $\begin{matrix} \sqrt[]{6} \end{matrix}$ i_max/2。

	Figure Option View Download New Window
	图4 线电流与相电流的时域向量图Fig.4 Time domain vector of line current and phase current

各绕组模式的工作范围受到电压矢量和电流矢量的限制。星形、角形模式不设弱磁区; 独立模式分为非弱磁区和弱磁区, 定子电压发生饱和便进入弱磁区, 以提升电机的调速范围。在各模式的非弱磁区, 采用最大转矩电流比(Maximum torque per ampere, MTPA)控制^[11]; 弱磁区采用前馈磁通控制, 根据当前电机转子速度ω _s指定定子磁链幅值 $\begin{matrix} ψ_{s}^{*} \end{matrix}$ , 再根据需求转矩 $\begin{matrix} T_{e}^{*} \end{matrix}$ 计算d、q轴期望电流 $\begin{matrix} i_{d}^{*} \end{matrix}$ 、 $\begin{matrix} {i_{q}^{*}}^{[12]} \end{matrix}$ 。

开绕组电机驱动系统的主要参数如下:转子极对数p₀=4; 定子绕组电阻R_s=0.1 Ω ; 永磁体磁链幅值ψ _f=0.2 Wb; d轴电感L_d=0.0012 F; q轴电感L_q=0.0015 F; 电源1母线电压V_dc1=240 V; 电源2母线电压V_dc2=230 V; IGBT器件电流容量i_max=160 A。

在上述电流控制策略下各绕组模式的外特性曲线如图5所示。

	Figure Option View Download New Window
	图5 各绕组模式的外特性曲线Fig.5 External characteristic curve of each winding mode

可以看出, 角形模式的调速范围大致是星形模式的 $\begin{matrix} \sqrt[]{3} \end{matrix}$ 倍, 最大转矩是星形模式的1/ $\begin{matrix} \sqrt[]{3} \end{matrix}$ 倍; 独立模式非弱磁区的调速范围大致是星形模式的2倍, 最大转矩与星形模式保持一致。

1.2 绕组模式切换策略

首先确定绕组切换的整体思路。星形和角形模式时只有一个逆变器参与工作, 另一逆变器处于下管全开的状态, 只有通态损耗; 但角形模式的三角形开关和零序电流会造成额外损耗。独立模式时, 两个逆变器都参与工作。从各模式所带来的器件损耗考虑, 在同样满足工况需求的前提下, 优先使用星型模式, 其次是角形模式, 尽量不采用独立模式。

在两电源电压差别不大时, 星形、角形和独立模式的非弱磁区最高转速依次升高。据此定义从星形到角形模式、从角形到独立模式、从星形到独立模式的切换为向上切换; 反之则为向下切换。

然后讨论向上切换策略。由于电机在运行过程中, 磁链、电感等参数会受到温度升高等的影响而产生小幅变化, 各模式工作范围会改变; 另外为了避免当电机工作点小幅变化时, 模式之间频繁切换, 提出一种转矩饱和判定算法, 判定成立时触发绕组模式向上切换, 以最大限度保证切换边界的准确性。

转矩饱和判定考虑电机转矩从0升至正最大值这一极限过程, 计算当前模式下(星形或角形), 期望转矩为正最大时, 电磁转矩在当前转速下从0调节至期望值时间t_int作为积分时间, 以及此过程中转矩偏差Δ T(实际输出转矩T_l与期望转矩 $\begin{matrix} T_{e}^{*} \end{matrix}$ 的差值)绝对值的积分I_th作为门限; 然后计算从t_int之前到当前时刻的实际转矩偏差Δ T绝对值的积分I, 并与I_th进行比较。若I≥ I_th, 则认为当前电机转矩已经趋于饱和, 无法跟随期望转矩, 转矩饱和判定成立。转矩饱和判定算法以电机输出转矩是否能够在限定时间内跟随期望转矩作为判断依据, 避免了电机参数变化带来的各绕组模式工作范围不确定的问题。

在d、q坐标下电机电压方程由式(2)(3)表述:

u_d=R_si_d+L_d $\begin{matrix} \frac{d i_{d}}{dt} \end{matrix}$ -ω _rL_qi_q(2)

u_q=R_si_q+L_q $\begin{matrix} \frac{d i_{q}}{dt} \end{matrix}$ +ω _r(L_di_d+ψ _f) (3)

电磁转矩表达式由式(4)表述:

T_e=p₀i_q[ψ _f+(L_d-L_q)i_d](4)

电磁转矩T_e主要由i_q所决定; 且d、q轴的电感差异越小, i_q所占份额就越大。当有L_d=L_q时, MTPA控制即为i_d=0控制。所以为计算方便, 转矩积分时间t_int的推导按i_d=0控制进行; 当L_d与L_q相差不大时, 将所推导的t_int应用于MTPA控制准确性依然较高; 且因L_q≥ L_d, 按i_d=0控制规律推导的积分时间t_int偏大, 转矩饱和判定偏保守。

使用i_d=0控制时, 由于d轴电流为零, 电压矢量幅值u_s满足:

$\begin{matrix} u_{s}^{2} \end{matrix}$ = $\begin{matrix} u_{d}^{2} \end{matrix}$ + $\begin{matrix} u_{q}^{2} \end{matrix}$ = $\begin{matrix} (- ω_{r} L_{q} i_{q})^{2} \end{matrix}$ +(R_si_q+L_q $\begin{matrix} \frac{d i_{q}}{dt} \end{matrix}$ +ω _rψ _f)² (5)

当电压矢量幅值为最大值u_s_max时, 从式(5)可解得q轴电流变化率为:

$\begin{matrix} \frac{d i_{q}}{dt} \end{matrix}$ = $\begin{matrix} \frac{\sqrt[]{u_{smax}^{2} - (ω_{r} L_{q} i_{q})^{2}} - ω_{r} ψ_{f} - R_{s} i_{q}}{L_{q}} \end{matrix}$ (6)

由于电机机械惯性远大于电气惯性, 可认为式中ω _r为常数; 但di_q/dt实时变化。将i_q取最大值i_smax使得di_q/dt为最小值, 使t_int偏大, 令判定偏保守。并忽略定子电阻R_s, 于是di_q/dt近似为:

$\begin{matrix} \frac{d i_{q}}{dt} \end{matrix}$ = $\begin{matrix} \frac{\sqrt[]{u_{smax}^{2} - (ω_{r} L_{q} i_{smax})^{2}} - ω_{r} ψ_{f}}{L_{q}} \end{matrix}$ (7)

随着电机转子速度ω _r的升高, 运动电动势的分压变大, 定子电压逐渐趋于饱和, 能用于使电流变化的电压裕量越来越小, 从而导致di_q/dt变小; 当ω _r接近最大值时, di_q/dt趋近于0, 意味着驱动系统逐渐丧失对电机电流的控制能力。为保留用于控制电机电流的电压裕量, 通过下式从基速按比例取各绕组模式下计算di_q/dt所用的转子速度ω _rs:

ω _rs=k_sω _rb(8)

式中:ω _rb是当前绕组模式下的电机转子角速度基速, 在i_d=0控制策略下忽略R_s有:

ω _rb= $\begin{matrix} \frac{u_{smax}}{ψ_{s}} \end{matrix}$ = $\begin{matrix} \frac{u_{smax}}{\sqrt[]{ψ_{f}^{2} + (L_{q} i_{smax})^{2}}} \end{matrix}$ (9)

由于近似后di_q/dt为常数, 则积分时间t_int为:

t_int= $\begin{matrix} \frac{Δ i_{q}}{d i_{q} / dt} \end{matrix}$ = $\begin{matrix} \frac{L_{q} i_{smax}}{\sqrt[]{u_{smax}^{2} - (k_{s} ω_{rb} L_{q} i_{smax})^{2}} - k_{s} ω_{rb} ψ_{f}} \end{matrix}$ (10)

式中:k_s∈ (0, 1)是转子速度敏感系数; k_s越大, 计算t_int使用的转子速度k_sω _rb越趋近于基速, 电压裕量越小, di_q/dt越小, 使得t_int越大; k_s反映了对转矩跟随速度的容忍程度, k_s越大, 对转矩跟随速度的要求越低, 但也使转矩饱和判定反应越慢; i_smax为当前绕组模式下的定子电流矢量最大幅值; u_smax为当前模式下可用电压矢量最大幅值。

由于近似后的di_q/dt为常数, 转矩跟随过程近似为线性过程, 则该极限过程的转矩偏差积分值为:

I_lim= $\begin{matrix} \int_{0}^{t_{int}} \end{matrix}$ |Δ Tdt|= $\begin{matrix} \int_{0}^{t_{int}} \end{matrix}$ |T_l- $\begin{matrix} T_{e}^{*} \end{matrix}$ |dt= $\begin{matrix} \frac{1}{2} \end{matrix}$ T_emaxt_int (11)

设定敏感系数k_I, 使实际的积分门限值I_th为:

I_th=k_II_lim= $\begin{matrix} \frac{1}{2} \end{matrix}$ k_IT_emaxt_int= $\begin{matrix} \frac{1}{2} \end{matrix}$ k_Ip₀ψ _fi_smaxt_int (12)

式中:T_emax是当前绕组模式下的最大电磁转矩。积分门限敏感系数k_I∈ (0, 1], k_I值越大, I_th越大, 转矩饱和判定越不敏感, 可以减小误切换的概率, 但会增大转矩切换的延迟; 反之, 转矩饱和判定越敏感, 可以使转矩切换迅速, 但可能会导致工况变化剧烈时的误切换。通过改变k_s与k_I这两个系数可以调节转矩饱和判定的敏感度与稳定性。

转矩饱和判定算法的程序框图如图6所示。

角形模式向上切换的终点只有独立模式, 所以当转矩饱和条件满足时就可触发到独立模式的切换。但星形模式向上切换有角形和独立模式两个终点; 当转矩饱和判定满足时, 需继续根据定子电流的饱和程度决定切换终点。当定子电流矢量幅值i_s≥ i_smaxΔ时, 表明当前定子电流矢量幅值已超过角形模式的调制能力, 此时向上切换终点应为独立模式; 同理, 若有i_s< i_smaxΔ, 切换终点应为角形模式。

	Figure Option View Download New Window
	图6 转矩饱和判定算法程序框图Fig.6 Flow chart of torque saturation decision algorithm

绕组模式向下切换采用转速门限值规则, 即用各绕组模式的基速作为门限值, 当电机转速降到星形或角形模式的基速以下时触发向下切换; 使得向上与向下切换的电机工作点错开, 避免了频繁切换。

向下切换除了依据电机转速以外, 也需继续根据定子电流矢量的饱和程度确定是否切换。无论是角形还是独立模式, 只要当电机转速满足n_r< n_bY, 就可触发到星形模式的切换。但独立模式的转速满足n_bY≤ n_r< n_b_Δ时, 需要判断是否可以切换到角形模式。当定子电流矢量幅值i_s≥ i_s_maxΔ时, 表明当前定子电流已超过角形模式的调制能力, 应保持绕组模式为独立模式不变; 若有i_s< i_smaxΔ, 则可触发向角形模式的切换, 其中n_bY为星形模式的电机基速; n_b_Δ为角形模式的电机基速。

各绕组模式之间的切换规则总结在表1中。其中Ω _br指星形模式的电机基速, Ω _bΔ指角形模式的电机基础速。

表1 各绕组模式之间的切换规则 Table 1 Shifting algorithm of each winding mode

2 双逆变器电流调制方法

本文采用以滞环控制为基础的电流调制方法。在单电源供电的星形和角形模式下, 逆变器每相桥臂只能提供2个电平, 采用传统滞环电流调制即可; 在独立模式, 双逆变器协同控制可提供3或4个电平, 故提出一种多电平滞环电流调制方法。

2.1 星形和角形模式的电流调制方法

星形模式时单侧逆变器每相桥臂下管同时打开; 另一侧逆变器正常工作, 对三相电流进行控制。根据期望转矩 $\begin{matrix} T_{e}^{*} \end{matrix}$ 按照前述MTPA和弱磁电流控制策略得到控制 $\begin{matrix} i_{d}^{*} \end{matrix}$ 和 $\begin{matrix} i_{q}^{*} \end{matrix}$ 后, 通过坐标变换即可获得三相电流的期望值 $\begin{matrix} i_{A}^{*} \end{matrix}$ 、 $\begin{matrix} i_{B}^{*} \end{matrix}$ 、 $\begin{matrix} i_{C}^{*} \end{matrix}$ , 同时根据电流传感器获得当前相电流实际值i_A、i_B、i_C。相电流偏差代表了每相电流实际值与期望值的差, 由下式定义:

$\begin{matrix} \{\begin{matrix} Δ i_{A} = i_{A} - i_{A}^{*} \\ Δ i_{B} = i_{B} - i_{B}^{*} \\ Δ i_{C} = i_{C} - i_{C}^{*} \end{matrix} \end{matrix}$ (13)

根据每相电流偏差, 对三相电流分别进行控制。设置电流滞环带的半宽, 即允许的电流偏差值为h。当相电流偏差Δ i≥ h时, 触发该相逆变器桥臂上管关断下管导通, 使该相中点电压为-V_dc/2, 促使该相相电流偏差Δ i减小; 相电流偏差Δ i≤ -h时, 触发该相逆变器桥臂上管导通下管关断, 使该相中点电压为V_dc/2, 促使该相相电流偏差Δ i增大。

角形模式时关断一侧电源并打开附加的三角形开关; 另一侧逆变器正常工作, 对电机线电流进行控制, 从而间接控制电机相电流。通过式(1)就可以把三相电流的期望值 $\begin{matrix} i_{A}^{*} \end{matrix}$ 、 $\begin{matrix} i_{B}^{*} \end{matrix}$ 、 $\begin{matrix} i_{C}^{*} \end{matrix}$ 转化为线电流期望值 $\begin{matrix} i_{1}^{*} \end{matrix}$ 、 $\begin{matrix} i_{2}^{*} \end{matrix}$ 、 $\begin{matrix} i_{3}^{*} \end{matrix}$ , 然后确定线电流偏差Δ i₁、Δ i₂、Δ i₃, 便可对3个线电流分别进行滞环控制。

如果忽略零序电流, 即有 i_A+i_B+i_C=0成立, 则可由式(1)得到由线电流表示的相电流:

$\begin{matrix} \{\begin{matrix} i_{A} = (i_{1} - i_{2} \frac{)}{3} \\ i_{B} = (i_{2} - i_{3} \frac{)}{3} \\ i_{C} = (i_{3} - i_{1} \frac{)}{3} \end{matrix} \end{matrix}$ (14)

如果允许的线电流偏差值为h_l, 则i₁-i₂的允许偏差值为2h_l, 进而有相电流i_A=(i₁-i₂)/3的允许偏差值为2h_l/3。可见, 若保持相电流的允许偏差值为h不变, 需要设定线电流滞环带半宽为3h/2, 即:

h_l= $\begin{matrix} \frac{3}{2} \end{matrix}$ h(15)

此时, 若忽略零序电流, 角形模式的相电流跟踪误差与星形模式相同。但角形模式的母线电压是直接加到相电压上的; 在各逆变器开关组合下, 星形可能出现的相电压有-2V_dc/3、-V_dc/3、0、V_dc/3、2V_dc/3共5种电压, 而角形可能出现的相电压只有-V_dc、0、V_dc这3种电压, 且幅值比星形大。所以按上式指定滞环带半宽, 虽然角形模式的电流跟踪误差与星形相同, 但其电流锯齿状波动会比星形剧烈, 逆变器器件开关频率与电机的铁损也会大于星形模式。

2.2 独立模式的电流调制方法

独立模式不同于星形和角形模式, 是由两侧电源提供电压并由两个逆变器共同控制的, 所以每相绕组的两侧都可由逆变器桥臂控制电平, 可获得4种开关状态:即(10)、(01)、(11)、(00)。

开关状态第一位表示逆变器1对应桥臂状态, 第二位表示逆变器2对应桥臂状态; 上管导通下管关断用 “ 1” 表示, 上管关断下管导通用 “ 0” 表示。由于两电源完全隔离, 两侧电源中点电压差u_nm随开关组合的不同而变化, 各开关状态下的相电压值不唯一确定; 所以按u_nm=0时进行分析, 满足此条件时的相电压定义为中点相电压。则开关状态(10)、(01)、(11)、(00)所得的中点相电压分别为(V_dc1+V_dc2)/2、-(V_dc1+V_dc2)/2、(V_dc1-V_dc2)/2、-(V_dc1-V_dc2)/2。可见, 在V_dc1≠ V_dc2时, 通过双逆变器的控制可以使中点相电压获得4个电平; V_dc1=V_dc2时, 中点电压也可获得3个电平, 此时开关状态(11)和(00)获得的中点相电压均为0。

传统的滞环电流调制算法有2个电平, 与之对应设置Δ i≥ h和Δ i≤ -h这2个触发区域; 独立模式除上述的2个触发区域用于触发开关状态(01)和(10)外, 还需制定2条中间触发线, 用于触发开关状态(00)和(11)。设这2条触发线分别为Δ i=d和Δ i=-d。根据触发时控制中点相电压与电流偏差Δ i成正比的原则, d满足下式关系:

h: $\begin{matrix} \frac{V_{dc 1} + V_{dc 2}}{2} \end{matrix}$ =d: $\begin{matrix} \frac{V_{dc 1} - V_{dc 2}}{2} \end{matrix}$ (16)

即有:

d= $\begin{matrix} \frac{V_{dc 1} - V_{dc 2}}{V_{dc 1} + V_{dc 2}} \end{matrix}$ h(17)

当V_dc1> V_dc2时, 有d> 0; 反之当V_dc1< V_dc2时, 有d< 0; 当V_dc1=V_dc2时, d=0, 此时2条触发线在Δ i=0处重合。需指出, 独立模式4个电平中2个边界电平开关状态(10)、(01)的触发方式为Δ i处于相应区域, 目的是保证Δ i在边界电平较大相电压作用下能够迅速回到滞环带[-h, h]范围内; 2个中间电平开关状态(00)、(11)的触发方式为穿越相应的控制线, 而不考虑Δ i所处区域或穿越的方向, 目的是减缓Δ i波动速度, 在Δ i距离中心线(Δ i=0)较近时作用较小相电压, 避免Δ i频繁撞击滞环带边界。应用该调制方法时, Δ i在穿越控制线Δ i=± d之后, 变化率会降低, 直至再次撞击滞环带边界; 使电流变化更平缓, 器件开关频率更低。

在上述多电平滞环电流调制策略的基础上加以改进, 提出两种优化后的多电平滞环调制方法, 称为低开关频率方法和大功率差值方法。这两种方法都通过增加独立模式逆变器桥臂中间电平开关状态(00)和(11)的触发条件而达到相应效果。

由于独立模式是两个电源共同供电的, 涉及两电源之间功率分配的问题, 故提出主电源概念:主电源是指独立模式两个供电电源中期望输出功率较大者。低开关频率方法和大功率差值方法都可以指定主电源并随时切换, 实现电源间功率分配。在负载较小时, 甚至可以实现主电源向另一电源充电。表2说明了双逆变器桥臂开关组合、相电流i的方向与电量流动之间的关系。设图1中相电流从左向右为正, 可见, 只有逆变器桥臂处于2个中间电平的开关状态下, 才能实现电量在两电源间流动。

低开关频率方法与大功率差值方法的逆变器桥臂开关状态触发规律如表3所示。

这两种改进的方法都增加了2个中间电平的触发条件, 通常情况下在一个滞环周期只有一个中间电平被触发。低开关频率方法在Δ i穿越控制线Δ i=± d时, 需要确认切换后主电源对应的逆变器桥臂开关状态不变才会切换; 避免了Δ i穿越控制线时同时改变两侧桥臂的开关状态, 最大限度降低了逆变器器件开关频率。大功率差值方法在Δ i穿越控制线时, 需根据当前相电流i的方向判断是否切换; 以保证该相在中间电平状态时, 由主电源向另一电源充电; 最大限度提升了两个电源的输出功率差值, 即尽量提高主电源功率, 降低另一电源的输出功率。

表2 双逆变器桥臂开关状态与电量流动关系 Table 2 Relation between inverter switching states and power flow direction

表3 低开关频率方法与大功率差值方法逆变器桥臂开关组合触发规律 Table 3 Dual inverter trigger rules of two different current modulation methods

3 开放式绕组电机驱动系统仿真结果

在Matlab/Simulink平台下对开放式绕组电机驱动系统进行仿真, 其中开放式绕组电机基本参数如1.1节所示, 控制器基本参数如表4所示。

本次仿真使系统运行0.9 s, 电机期望转速在0~0.3 s线性升至5500 r/min, 并保持该值到0.6 s, 然后在0.6~0.9 s线性降至0; 负载转矩在0.05 s时从0阶跃至50 N· m, 并保持到仿真结束。为观察系统在独立模式下的功率分配效果, 在0.4 s时将电流调制方法由低开关频率方法切换至大功率差值方法, 在0.5 s时将主电源由电源1切换至电源2。

表4 控制器基本参数 Table 4 Basic parameters ofcotrollers

电机转矩、转速曲线如图7所示。可以看出, 电机转速能够平稳、迅速地跟随设定转速, 仅在0.05 s负载转矩阶跃处有轻微抖动, 绕组模式的切换几乎对转速跟随无影响; 电磁转矩T_e亦能够很好地跟随期望转矩 $\begin{matrix} T_{e}^{*} \end{matrix}$ ; 在当前电流跟随精度下(h=3 A), 电磁转矩波动幅度被限制在5 N· m左右, 但当0.5 s时主要供电电源切换为电压更低的电源2后, 转矩波动幅度略微增大。

	Figure Option View Download New Window
	图7 期望电机转矩、电机电磁转矩与电机转速曲线Fig.7 Curves of expected motor torque, electromagnetic torque and motor speed

绕组模式、转矩饱和判定积分门限I_th与实际积分值I曲线分别如图8(a)、8(b)所示。

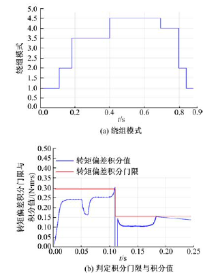	Figure Option View Download New Window
	图8 绕组模式、转矩饱和判定积分门限与积分值曲线Fig.8 Curves of winding mode, integral threshold and integral value of torque saturation decision

图8(a)中所示的模式信号, 1.0表示星形, 2.0表示角形, 3.0、4.0分别表示独立模式中的低开关频率方法和大功率差值方法, 3.5和4.5表明对应模式的弱磁区。从图8(a)可以看出, 从电磁转矩饱和到绕组模式向上切换在0.02 s内完成, 切换迅速果断。从图8(b)中也可看出, 向上切换前0.02 s左右, 随着电压逐渐饱和, 转矩偏差积分值迅速上升至门限, 触发模式的向上切换; 切换到角形模式后, 因转矩积分时间变小, 积分门限和积分值都有所降低。

A相电压在模式切换处的波形如图9(a)、9(b)所示; A相电流及其局部波形如图9(c)、9(d)所示。

星形、角形和独立绕组模式对应的相电压幅值依次升高; 从局部波形可看出, 相电压电平数星形多于角形, 独立模式最多, 控制更加细腻。电机相电流按正弦变化, 被严格限制在了滞环带范围内, 跟随精确; 电机从星形切换到角形模式后, 因零序电流的注入, 相电流波形发生了畸变, 这会导致逆变器额外容量的占用、器件开关频率增大等问题。

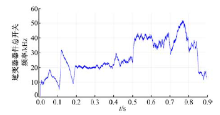
	Figure Option View Download New Window
	图9 电机A相电压、电流及其局部波形Fig.9 Curves and partial waves of voltage phase A's voltage and current

逆变器器件总开关频率(即所有IGBT器件的开关频率之和)曲线如图10所示。可以看出, 角形模式的器件开关频率大于星形, 这是由于前述角形模式电机的相电压电平数目少且幅值大, 导致相电流变化率偏大, 从而使相电流更加频繁地触碰滞环带边界所致; 因独立模式需要两个逆变器一起工作, 所以器件总开关频率也较大; 但独立模式的相电压电平数目更多, 对相电流的控制更加细腻, 有助于降低器件开关频率。0.4 s电流调制方法由低开关频率切换至大功率差值方法后, 器件总开关频率略有增加; 0.5 s主电源从电源1切换至电压较低的电源2后, 总开关频率出现了幅度更大的增加; 这说明了令电压更高的电源作为主电源有利于降低器件开关频率。此外, 稳态时器件总开关频率低于瞬态时, 电机转速上升时的器件总开关频率低于电机转速下降时。

	Figure Option View Download New Window
	图10 逆变器器件总开关频率曲线Fig.10 Curves of inverter total switching frequency

两侧逆变器输入功率曲线如图11所示。可以看出, 0.5 s以前电源1为主电源, 星形和角形模式由电源1单独供电, 总输入功率全部来自于逆变器1; 0.5 s以后电源2为主电源, 星形和角形模式由电源2单独供电, 总输入功率全部来自于逆变器2。绕组模式为独立模式时, 两电源共同提供功率; 0.4 s电流调制方法由低开关频率方法切换至大功率差值方法后, 两个逆变器的功率差值变大; 0.5 s主电源从电源1切换至电源2后, 逆变器2的功率超过逆变器1的功率, 成为主要输出功率一方; 但因电源2电压低于电源1电压, 主电源切换至电源2后, 两个逆变器的功率差值变小, 说明逆变器的功率差值受到两电源电压差值影响。

	Figure Option View Download New Window
	图11 两侧逆变器输入功率曲线Fig.11 Curves of input power of both inverters

4 结束语

针对电动车用双电源双逆变器开绕组永磁同步电机驱动系统, 提出了3种绕组模式及实现方法。在分析各绕组模式电机外特性的基础上, 制定了绕组模式切换策略, 其中的转矩饱和判定算法可实现绕组模式自动向上切换, 避免了电机参数变化导致的切换点不准确问题。所提的用于独立模式多电平电流滞环调制算法, 相较传统滞环控制增加了电平数量及触发机制, 可指定主电源并实时切换, 从而实现两电源间的能量分配; 其具有的低开关频率和大功率差值两种控制方式, 可实现不同的节能与能量分配效果。仿真结果表明:转矩饱和判定算法可以在电磁转矩无法跟随期望值时迅速触发模式向上切换, 过程迅速; 多电平电流滞环调制算法可令主电源输出更大功率, 但功率差值受到电源电压差值影响。仿真结果表明本文方法充分利用了各绕组模式的工作区间, 减少了器件损耗并提高了系统效率, 为双电源构型下车用动力系统的建立提供了理论依据与工程方案。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Nguyen N K, Semail E, Meinguet F, et al. Different virtual stator winding configurations of open-end winding five-phase PM machines for wide speed range without flux weakening operation[C]∥European Conference on Power Electronics and Applications, 2013: 1-8. [本文引用:1]
[2]	Welchko Brian A, Nagashima James M. The influence of topology selection on the design of EV/HEV propulsion systems[J]. IEEE International Symposium on Industrial Electronics (ISIE), 2003, 99(2): 36-40. [本文引用:1]
[3]	安群涛, 孙力, 孙立志. 新型开放式绕组永磁同步电机矢量控制系统研究[J]. 中国电机工程学报, 2015, 35(22): 5891-5898. An Qun-tao, Sun Li, Sun Li-zhi. Research on novel open-end winding permanent magnet synchronous motor vector control systems[J]. Proceedings of the CSEE, 2015, 35(22): 5891-5898. [本文引用:1]
[4]	Rossi C, Grand i G, Corbelli P, et al. Generation system for series hybrid powertrain based on the dual two-level inverter[C]∥European Conference on Power Electronics and Applications, IEEE, Barcelona, Spain, 2009: 1-10. [本文引用:1]
[5]	安群涛, 姚飞, 孙立志, 等. 双逆变器SVPWM调制策略及零序电压抑制方法[J]. 中国电机工程学报, 2016, 36(4): 1042-1049. An Qun-tao, Yao Fei, Sun Li-zhi, et al. SVPWM strategy of dual inverters and zero-sequence voltage suppression method[J]. Proceedings of the CSEE, 2016, 36(4): 1042-1049. [本文引用:1]
[6]	年珩, 曾恒力, 周义杰. 共直流母线开绕组永磁同步电机系统零序电流抑制策略[J]. 电工技术学报, 2015, 30(20): 40-48. Nian Heng, Zeng Heng-li, Zhou Yi-jie. Zero sequence current suppression strategy for open winding permanent magnet synchronous motor with common DC bus[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 40-48. [本文引用:1]
[7]	孙丹, 林斌, 陈敏, 等. HEV用开绕组永磁同步电机双逆变器协同控制[J]. 电机与控制学报, 2016, 20(2): 29-35. Sun Dan, Lin Bin, Chen Min, et al. Coordinate control of dual-inverter driven open-winding PMSM for hybrid electric vehicles[J]. Electric Machines and Control, 2016, 20(2): 29-35. [本文引用:1]
[8]	Welchko B A, Nagashima J M. A comparative evaluation of motor drive topologies for low-voltage, high-power EV/HEV propulsion systems[C]∥IEEE International Symposium on Industrial Electronics, Rio de Janeiro, Brazil, 2003: 379-384. [本文引用:1]
[9]	Casadei D, Grand i G, Lega A, et al. Multilevel operation and input power balancing for a dual two-level inverter with insulated DC sources[J]. IEEE Transactions on Industry Applications, 2008, 44(6): 1815-1824. [本文引用:1]
[10]	Griva G, Oleschuk V, Profumo F. Hybrid traction drive with symmetrical split-phase motor controlled by synchronized PWM[C]∥International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Ischia, Italy, 2008: 1033-1037. [本文引用:1]
[11]	李长红, 陈明俊, 吴小役. PMSM调速系统中最大转矩电流比控制方法的研究[J]. 中国电机工程学报, 2005, 25(21): 172-177. Li Chang-hong, Chen Ming-jun, Wu Xiao-yi. Study of maximum ratio of torque to current control method for PMSM[J]. Proceedings of the CSEE, 2005, 25(21): 172-177. [本文引用:1]
[12]	Krishnan R. Control and operation of PM synchronous motor drives in the field-weakening region[C]∥International Conference on Industrial Electronics, Control, and Instrumentation, Maui, HI, USA 1993: 745-750. [本文引用:1]

2013

0.0

... 近年来开绕组永磁同步电机(OW-PMSM)^[1,2]及其与双逆变器组成的驱动系统^[3,4]获得了广泛的应用 ...

2003

0.0

... 近年来开绕组永磁同步电机(OW-PMSM)^[1,2]及其与双逆变器组成的驱动系统^[3,4]获得了广泛的应用 ...

2015

0.0

. 2015, 35(22):5891-5898 DOI:doi:10.13334/j.0258-8013.pcsee.2015.22.025

Research on novel open-end winding permanent magnet synchronous motor vector control systems

新型开放式绕组永磁同步电机矢量控制系统研究

An Qun-tao , Sun Li , Sun Li-zhi.

安群涛, 孙力, 孙立志

Open-end winding permanent magnet synchronous motors (OEW-PMSMs) fed by dual inverters as a kind of novel drive topology have competitive application prospects in the electric drive field for their high utility of DC-link voltage, more control freedoms of currents and good fault-tolerant ability. The mathematic model and vector control system fed by the dual inverter of OEW-PMSMs were built. Based on the principle and output voltage vectors of the dual inverter, the zero-sequence voltage and current were analyzed, and a SVPWM switching strategy which employs voltage vectors that do not contribute to zero-sequence voltage was proposed to eliminate zero-sequence voltage. And, its implement algorithm was discussed. The basic speed of the OEW-PMSM fed by the dual inverter with the zero-sequence voltage eliminated SVPWM strategy can be improved to 1.7 times of the star-connected winding permanent magnet synchronous motor (SCW-PMSM). Therefore, the difficulty of their flux-weakening design and control can be reduced greatly. The proposed method is validated by simulation and experimental results.

双逆变器供电的开放式绕组永磁同步电机(open-end winding permanent magnet synchronous motor,OEW-PMSM)系统作为一种新型电机驱动拓扑,其直流母线电压利用率高、绕组电流控制自由度大、容错能力强,在电力拖动领域具有良好的应用价值。该文建立了OEW-PMSM的数学模型及其采用双逆变器供电的矢量控制系统,结合双逆变器工作原理和输出矢量,分析系统零序电压和零序电流问题,采用不产生零序电压的电压矢量进行空间矢量脉宽调制(space vector pulse width modulation,SVPWM)来消除零序电压,并给出实现算法。在采用消除零序电压的SVPWM控制时,双逆变器供电的OEW-PMSM可以将基速提高为星接绕组时的1.7倍,降低了系统弱磁设计和控制的难度。仿真和实验验证了所提方法的正确性和可行性。

... 近年来开绕组永磁同步电机(OW-PMSM)^[1,2]及其与双逆变器组成的驱动系统^[3,4]获得了广泛的应用 ...

2009

0.0

... 近年来开绕组永磁同步电机(OW-PMSM)^[1,2]及其与双逆变器组成的驱动系统^[3,4]获得了广泛的应用 ...

2016

0.0

. 2016, 36(4):1042-1049 DOI:doi:10.13334/j.0258-8013.pcsee.2016.04.019

SVPWM strategy of dual inverters and zero-sequence voltage suppression method

双逆变器SVPWM调制策略及零序电压抑制方法

An Qun-tao , Yao Fei , Sun Li-zhi

安群涛, 姚飞, 孙立志

The dual inverter has the same distribution of space voltage vectors with three-level inverters, and the utilization of DC link voltage is improved. Therefore, the dual inverter is widely applied in open-end winding motor drive systems. Based on the analysis of principle of the dual inverter, modulation strategies were researched and a dual inverter space vector pulse width modulation (SVPWM) strategy in maximum voltage range was proposed. In the proposed strategy, the plane can be divided into six sectors and then the voltage vector reference can be divided into two parts. One part is equivalent to a special switching state clamped by one inverter, and the other part is modulated by the other inverter in the six sub-sectors divided further in each sector. In order to suppress the zero-sequence voltage, a factor was introduced to redistribute zero voltage vectors during the synthesis. The zero-sequence voltage produced by basic voltage vectors can be counteracted by that of the redistributed zero voltage vectors. Simulation model and experimental bench of the vector-controlled open-end winding permanent magnet synchronous motor drive system were built, and the simulation results as well as experimental ones validate the proposed method.

双逆变器具有与三电平逆变器相同的空间电压矢量分布,使直流母线电压利用率提高,在开放式绕组电机驱动系统中得到广泛应用。该文在分析双逆变器工作原理的基础上,研究双逆变器的调制策略,提出一种最大电压范围的双逆变器空间矢量脉宽调制(space vector pulse width modulation,SVPWM)策略,该策略首先将空间电压矢量平面划分为6个扇区,从而将参考电压矢量分解为两段：其中一段矢量等效为将双逆变器中的一个逆变器钳位在某一特定开关状态;另一段矢量由另外一个逆变器在其6个子扇区内调制实现。为抑制SVPWM调制所带来的零序电压,引入等效零矢量分配因子,通过零矢量产生的零序电压来抵消基本电压矢量合成时产生的零序电压。在开放式绕组永磁同步电机矢量控制系统中进行了仿真和实验研究,仿真和实验结果证明了所提方法的有效性。

... 该系统通过在开绕组电机定子绕组两端各连接一个逆变器进行驱动,相比传统永磁同步电机驱动系统扩展了调速范围并可采用更灵活的控制方法^[5,6] ...

2015

0.0

. 2015, 30(20):40-48

Zero sequence current suppression strategy for open winding permanent magnet synchronous motor with common DC bus

共直流母线开绕组永磁同步电机系统零序电流抑制策略

Nian Heng , Zeng Heng-li , Zhou Yi-jie.

年珩, 曾恒力, 周义杰

由于变流器调制产生的共模电压和永磁电机反电动势三次谐波的存在,开绕组永磁同步电机两端共直流母线情况下会在电机绕组产生零序电流,影响了电机运行效率和稳定性。由此提出了共直流母线开绕组永磁同步电机系统零序电流抑制策略,通过建立开绕组永磁同步电机数学模型,分析了零序回路的工作特性,并通过对零序电流的闭环调节控制变流器产生共模电压以抵消反电动势三次谐波分量,达到抑制零序电流的目的;同时深入分析和对比了所提零序电流抑制策略和传统共模电压抑制策略的调制能力和最大调制度;最后,通过构建开绕组永磁同步电机实验机组,对所提零序电流抑制策略的可行性和有效性进行了实验验证。

... 该系统通过在开绕组电机定子绕组两端各连接一个逆变器进行驱动,相比传统永磁同步电机驱动系统扩展了调速范围并可采用更灵活的控制方法^[5,6] ...

2016

0.0

. 2016, 20(2):29-35

Coordinate control of dual-inverter driven open-winding PMSM for hybrid electric vehicles

HEV用开绕组永磁同步电机双逆变器协同控制

Sun Dan , Lin Bin , Chen Min

孙丹, 林斌, 陈敏

... 并允许两个逆变器从不同电源取电,双电源场合应用时在省去DC/DC变换器的同时可实现电源间的能量分配^[7,8,9,10] ...

2003

0.0

... 并允许两个逆变器从不同电源取电,双电源场合应用时在省去DC/DC变换器的同时可实现电源间的能量分配^[7,8,9,10] ...

2008

0.0

... 并允许两个逆变器从不同电源取电,双电源场合应用时在省去DC/DC变换器的同时可实现电源间的能量分配^[7,8,9,10] ...

2008

0.0

... 并允许两个逆变器从不同电源取电,双电源场合应用时在省去DC/DC变换器的同时可实现电源间的能量分配^[7,8,9,10] ...

2005

0.0

. 2005, 25(21):172-177

Study of maximum ratio of torque to current control method for PMSM

PMSM调速系统中最大转矩电流比控制方法的研究

Li Chang-hong , Chen Ming-jun , Wu Xiao-yi.

李长红, 陈明俊, 吴小役

... 在各模式的非弱磁区,采用最大转矩电流比(Maximum torque per ampere,MTPA)控制^[11] ...

1993

0.0