多点冲头主动加载路径对薄板拉形的影响

引用本文

刘纯国, 刘伟东, 邓玉山. 多点冲头主动加载路径对薄板拉形的影响[J].吉林大学学报（工学版）, 2018,48(1): 221-228
LIU Chun-guo, LIU Wei-dong, DENG Yu-shan. Effect of multi-point punch active loading path on the stretch-forming of sheet[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 221-228 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170021
Permissions

多点冲头主动加载路径对薄板拉形的影响

刘纯国, 刘伟东, 邓玉山

吉林大学辊锻工艺研究所,长春 130022

作者简介:刘纯国(1970-),男,教授,博士生导师. 研究方向:板料成形. E-mail:liucg@jlu.edu.cn

基金:国家自然科学基金项目(51575231)

摘要

研究了多点拉形过程中3种加载路径对板料拉形质量的影响。基于平面应变假设,对多点拉形和等差曲率冲头主动加载拉形中铝合金薄板的受力特点进行了对比分析,同时应用数值模拟研究了多点拉形与多点冲头主动加载拉形中3种路径对板料应力、应变及延伸率分布的影响规律。结果表明:与多点拉形相比,等速冲头主动加载、等时冲头主动加载及等差曲率冲头主动加载3种拉形方式均能减小板料钳口处的应力集中,提高工件的应力、应变、延伸率分布均匀性,其中等差曲率冲头主动加载路径拉形效果最好。

关键词: 材料合成与加工工艺; 多点模具; 加载路径; 拉形; 数值模拟

中图分类号:TG386.41 文献标志码:A 文章编号:1671-5497(2018)01-0221-08

Effect of multi-point punch active loading path on the stretch-forming of sheet

LIU Chun-guo, LIU Wei-dong, DENG Yu-shan

Roll Forging Research Institute, Jilin University, Changchun 130022,China

Abstract

In This paper the influences of three different loading paths on the quality of stretch- forming were studied. Based on the plane strain assumption, the s tress state of Al alloy sheet between multi-point stretch-forming and equidifferent-curvature punch active loading stretch-forming were compared and analyzed. The strain, stress, elongation distribution of the multi-point stretch-forming and the multi-point punch active loading stretch-forming under three different loading conditions were studied by numerical simulation. Results show that, compared with the multi-point stretch-forming, constant velocity punch active loading, isochronous punch active loading and equidifferent-curvature punch active loading can not only reduce the stress concentration in the position between the sheet and jaw, but also improve the uniformity of the distribution of stress, strain and elongation. The results confirm that equidifferent-curvature punch active loading method can achieve the best formability of Al alloy sheet.

Keyword: materials synthesis and processing technology; multi-point die; loading path; stretch-forming; numerical simulation

Show Figures

0 引言

与传统蒙皮拉形相比, 多点拉形中的拉形模具由一系列规则排列、高度可调的基本体组成, 快速可调的模具型面能够用于不同零件的柔性拉形^{[1, 2, 3, 4]}。多点拉形模具在成形前将基本体冲头调整到目标位置, 成形过程中基本体之间无相对运动, 多点模具替代传统模具, 在拉伸机的作用下将板料拉伸至完全贴模。这种成形方式能够节省模具制造成本, 缩短零件制造周期, 但多点拉形与传统拉形存在相同的局限性, 由于传力区与拉形模不接触, 板料与模具表面之间没有摩擦, 毛料易变薄, 夹头处应力集中较严重, 零件成形后应力和应变分布均匀性有待进一步提高^{[5, 6, 7, 8, 9]}。

随着多点模具技术的发展, 其中的基本体冲头能够在承受一定力的条件下实现高度的调整。每个冲头在受到板料预拉伸载荷的作用下, 按照设定的速度调整到目标高度。所有冲头的调整过程形成了一种对板料垂直方向的加载过程, 使得板料在横向拉伸力和垂向加载力的作用下变形。在保证模具型面几何连续的前提下, 模具中多点冲头的不同调形速度形成了不同的加载路径。该方法能够用于铝合金薄板的拉形, 通过设计不同的多点模具冲头主动加载路径和控制拉伸力, 能够使板料变形均匀, 消除成形缺陷。

本文以每个冲头对板料的加载速度和型面曲率控制为目标, 设计了3种不同的多点冲头主动加载路径。通过理论分析和有限元模拟, 研究了3种冲头主动加载路径下的拉形与多点拉形对工件成形质量的影响。

1 多点冲头主动加载路径设计

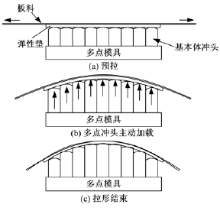
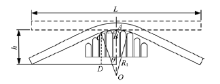
如图1所示, 多点模具初始型面为平面, 在板料预拉伸状态下, 通过控制基本体冲头的力、速度和位移参数, 连续改变模具型面, 对板料逐渐加载, 直至达到目标曲面形状。在多点冲头主动向上加载过程中, 两侧夹钳不会对板料主动施加拉力, 只是随着板料变形被动旋转, 不存在水平和竖直方向的位移变化。

在多点冲头主动加载拉形中, 成形之前对板料进行预拉伸; 成形过程中多点冲头主动向上运动, 对板料施加载荷, 同时夹钳随板料被动旋转, 直到形成最终目标形状。

	Figure Option View Download New Window
	图1 多点冲头主动加载拉形Fig.1 Multi-point punch active loading stretch-forming

由于在多点冲头主动加载拉形中, 工件的成形质量与每个冲头对板料的加载时间、加载速度及板料的曲率变化等均有密切关系。因此本文设计了以下3种加载路径:

(1)等速冲头主动加载

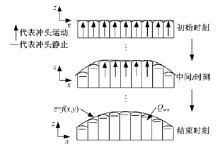
在这种成形方式中, 多点模具的基本体冲头在受力状态下主动改变各自的高度。初始时全部冲头以相等的速度运动, 当高度较低的冲头达到目标曲面位置时停止运动, 并保持位置不变, 其余冲头继续以相同的速度运动, 直到全部冲头达到目标位置。该加载过程形成一系列等高线, 从低到高连续加载, 如图2所示。

	Figure Option View Download New Window
	图2 等速冲头主动加载过程示意图Fig.2 Schematic diagram of constant velocity punch active loading process

设成形的目标曲面:z=f(x, y) (1)

成形后第m行、第n列位置的冲头Q_mn对应的坐标位置是(x_mn, y_mn, z_mn), 冲头的最终位移为:

z_mn=f(x_mn, y_mn)(2)

根据预先设置好的冲头运行速度v和冲头对应的目标曲面高度z_mn可计算得出每个冲头的最大运行时间:

t_mn= $\begin{matrix} \frac{z_{mn}}{v} \end{matrix}$ (3)

这种成形方式冲头调整简单, 实现了对板料的连续加载, 板料从低到高逐渐形成目标曲面, 在几何上连续过渡, 最终完成工件的成形。

(2)等时冲头主动加载

多点模具中的冲头在高度调整时, 每个冲头都以各自的速度匀速运动, 但在相同的时刻到达目标曲面高度, 完成对板料的加载, 如图3所示。

	Figure Option View Download New Window
	图3 等时冲头主动加载过程示意图Fig.3 Schematic diagram of isochronous punch active loading process

设成形目标曲面同式(1)。

冲头最终位移同式(2)。

在多点模具冲头加载之前, 根据目标曲面高度z_mn和运行时间t, 可以计算出每一个冲头的运行速度:

v_mn= $\begin{matrix} \frac{z_{mn}}{t_{}} \end{matrix}$ (4)

该加载过程中, 相邻冲头之间的位移差随时间均匀变化, 板料在成形过程中形成一系列等差曲面, 实现了空间曲面连续变化的加载过程。这种加载方式与传统拉形相比增大了板料与模具的接触面积。

(3)等差曲率冲头主动加载

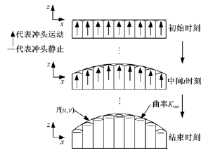
多点冲头在高度调整过程前, 首先分析目标曲面的曲率特征, 计算出多点冲头对应点处曲面的高斯曲率K_mn, 使成形过程中冲头对应位置的曲率随时间均匀变化, 如图4所示。

为便于进行求解, 可把目标曲面转换为B样条曲面进行表示:

$\begin{matrix} \overset{⇀}{r} \end{matrix}$ (u, v)= $\begin{matrix} \overset{p}{\sum_{i = 0}} \end{matrix} \begin{matrix} \overset{q}{\sum_{j = 0}} \end{matrix} \begin{matrix} {\overset{⇀}{V}}_{i, j} \end{matrix}$ N_i_,_k(u)N_j_,_l(v) (5)

式中: $\begin{matrix} {\overset{⇀}{V}}_{i, j} \end{matrix}$ 为控制点; N_i_,_k(u)和N_i_,_l(v)为基函数。

	Figure Option View Download New Window
	图4 等差曲率冲头主动加载过程示意图Fig.4 Schematic diagram of equidifferent-curvature punch active loading process

冲头在目标位置对应的高斯曲率为:

K_mn= $\begin{matrix} {\frac{LN - M^{2}}{EG - F^{2}}|}_{u = u_{mn}, v = v_{mn}} \end{matrix}$ (6)

式中:E、F、G为曲面第一基本形式参数; L、M、N为曲面第二基本形式参数。

为实现每个冲头对应位置处曲率均匀变化, 则需要构建随时间变化的过渡曲面。为保持形状的相似性对曲面设置随时间变化的系数b_i_,_j(t), 则t时刻过渡曲面形式为:

$\begin{matrix} \overset{⇀}{r} \end{matrix}$ (u, v)_t= $\begin{matrix} \overset{p}{\sum_{i = 0}} \end{matrix} \begin{matrix} \overset{q}{\sum_{j = 0}} \end{matrix}$ b_i_,_j(t) $\begin{matrix} {\overset{⇀}{V}}_{i, j} \end{matrix}$ N_i_,_k(u)N_j_,_l(v)(7)

式中:b_i_,_j(t)为函数中各单项式系数, 且均与时间相关。

对时间t求导即可得出每个冲头的运行速度:

v_mn= $\begin{matrix} {\frac{\partial \overset{⇀}{r}}{\partial t}|}_{u = u_{mn}, v = v_{mn}} \end{matrix}$ (8)

每个冲头按照得出的速度对板料进行加载, 即冲头按照对应位置的曲率均匀调整, 到达目标高度后停止运动。该加载过程在没有到达目标曲面前, 形成一系列曲率等差面, 实现了连续加载过程。在这种成形方式中, 板料形状曲率变化连续, 不存在曲率突变情况。

2 板料受力分析

基于平面应变做出如下假设:①单位宽度切向拉力沿板厚方向均匀分布, 该力使板料厚度减薄, 并使弯曲中性层向弯曲内表面移动②弯曲前垂直于板中性面的平面在弯曲后仍为平面, 且仍垂直于弯曲后板的中性面, 板料在宽度方向上的应变为零; ③板料不可压缩, 弯曲过程中板料纵向纤维之间无挤压, 即认为板料厚向应力为零^{[10, 11]}。

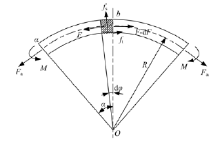
在拉形过程中任意选取部分单元进行受力分析建立平衡关系, 如图5所示。

	Figure Option View Download New Window
	图5 板料拉形力平衡示意图Fig.5 Force equilibrium scheme of stretch-forming

$\begin{matrix} \{\begin{matrix} Fcosdφ + f_{s} Rdφsin \frac{dφ}{2} = F - dF + f_{t} Rdφcos \frac{dφ}{2} \\ Fsindφ = f_{s} Rdφcos \frac{dφ}{2} + f_{t} Rdφsin \frac{dφ}{2} \\ f_{t} = μ f_{s} \end{matrix} \end{matrix}$ (9)

式中:F为板料任意截面处拉力; dF为拉力的微小变化; f_s为法向接触力分布密度; f_t为摩擦力分布密度; μ 为板料与凸模间的摩擦因数; R为板料弯曲中性层半径; dφ 为微小段板料弯曲角度。

对式(9)忽略无穷小项乘积, 可得:

$\begin{matrix} \{\begin{matrix} dF = f_{t} Rdφ \\ F = f_{s} R \\ f_{t} = μ f_{s} \end{matrix} \end{matrix}$ (10)

对式(10)进行简化, 并积分可得:

lnF=μ φ +C(11)

由a点边界条件:F=F_a, 对式(11)进行化简处理, 可得任意截面φ 处的拉力为:

F(φ )=F_ae^μ⁽^{φ -α}⁾(12)

(1)多点拉形

在这种拉形过程中, 把夹钳在垂直方向的移动距离h定义为多点拉形的拉伸变形量, 如图6所示, 其计算公式为:

h=AB+CD(13)

	Figure Option View Download New Window
	图6 多点拉形中间过程Fig.6 Intermediate process of multi-point stretch-forming

h=R₁-R₁cosθ +( $\begin{matrix} \frac{L}{2} \end{matrix}$ -R₁sinθ )tanθ (14)

式中:R₁为模具半径; θ 为贴模角度; L为初始板料长度。

(2)等差曲率冲头主动加载拉形

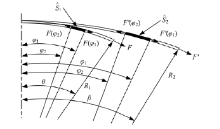
在这种拉形过程中, 把多点模具最高处冲头在垂直方向移动的距离h'定义为等差曲率冲头主动加载拉形的拉伸变形量, 如图7所示。

	Figure Option View Download New Window
	图7 等差曲率冲头主动加载拉形中间过程Fig.7 Intermediate process of equidifferent-curvature punch active loading stretch-forming

sinβ = $\begin{matrix} \frac{l / 2}{R_{2}} \end{matrix}$ (15)

h'=A'B'+C'D'(16)

h'=(R₂-R₂cosβ )+(L/2-l)tanβ (17)

式中:半径R₂为多点冲头形成的模具半径; β 为贴模角度; l为1/2模具的长度; L为板料初始长度。

当h=h'时, 基于上述两种拉形方式, 由式(14)(15)(17)得出:

β =θ $\begin{matrix} \sqrt[]{\frac{R_{1}^{3} + 8 L^{2} l + 3 L^{2}}{R_{2}^{3} + 8 L^{2} l + 3 L^{2}}} \end{matrix}$ (18)

由数学关系可知, 在成形过程中 β < θ 。

由上述计算可以得出两种拉形过程中面内拉力分布为:

F(φ )=Fe^μ⁽^{φ -θ}⁾(19)

F'(φ )=F'e^μ⁽^{φ -β}⁾(20)

	Figure Option View Download New Window
	图8 相同角度对应单元受力分析Fig.8 Force analysis of the same angle corresponding unit

任意选取对应相同角度部分单元进行截面受力分析, 如图9所示, 两种成形方式单位弧长内的受力均匀度分别为n和n'。

多点拉形:

n= $\begin{matrix} \frac{| F (φ_{1}) | - | F (φ_{2}) |}{F {\overset{}{s}}_{1}} \end{matrix}$ (21)

等差曲率冲头主动加载拉形:

n'= $\begin{matrix} \frac{| F' (φ_{1}) | - | F' (φ_{2}) |}{F' {\overset{}{s}}_{2}} \end{matrix}$ (22)

式中: $\begin{matrix} {\overset{}{s}}_{1} \end{matrix}$ 、 $\begin{matrix} {\overset{}{s}}_{2} \end{matrix}$ 为对应角度弧长。

受力均匀度越大说明板料受力分布越好, 越小说明板料受力分布越差, 将n和n'进行对比分析:

$\begin{matrix} \frac{n}{n'} \end{matrix}$ = $\begin{matrix} \frac{R_{2} (e^{μ (φ_{1} - θ)} - e^{μ (φ_{2} - θ)})}{R_{1} (e^{μ (φ_{1} - β)} - e^{μ (φ_{2} - β)})} \end{matrix}$ (23)

	Figure Option View Download New Window
	图9 多点冲头主动加载拉形有限元模型Fig.9 Multi-point punch active loading stretch-forming finite element model

根据e^x函数关系可知n< n', 说明当两种成形方式的拉伸变形量相同时, 等差曲率冲头主动加载拉形受力均匀程度优于多点拉形, 在整个拉形过程中都具有相同的规律。所以对于任意相同角度对应的板料, 等差曲率冲头主动加载拉形方式均能够起到使板料受力分布均匀的作用, 进而提高了应力应变分布均匀性。

3 多点冲头主动加载拉形有限元分析

3.1 材料力学参数和有限元模型

5083铝合金的力学性能通过拉伸实验获得, 其力学性能参数如下:密度ρ =2.79 g/cm³; 弹性模量E=68.9 GPa; 泊松比υ =0.31; 拉伸强度=158.3 MPa; 屈服强度=321.5 MPa。

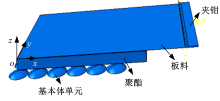
以半径为800 mm的球形件为例, 毛坯板料尺寸为600 mm × 420 mm × 2 mm。板料与基本体单元之间放置聚酯材料, 避免产生压痕。根据工件对称的特点, 将模型进行简化, 取模型的1/4进行分析, 从而节省时间, 提高分析效率。图9为多点冲头主动加载拉形有限元模型, 在板料中心位置建立坐标系o-xyz, ox平行于拉伸方向, oy垂直于拉伸方向。

3.2 模拟结果分析

(1)不同加载路径对板料钳口处应力集中的影响

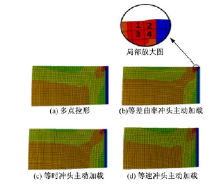
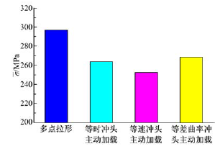
在拉形过程中, 多点模具的冲头加载路径对板料钳口处的应力集中有重要影响。4种不同成形方式得到的应力最大值都分布在靠近夹钳的边缘处, 如图10所示, 以最靠近夹钳边缘处的4个单元为计算依据, 定义了应力集中值 $\begin{matrix} \bar{σ} \end{matrix}$ :

$\begin{matrix} \bar{σ} \end{matrix}$ = $\begin{matrix} \overset{4}{\sum_{i = 1}} σ_{i} / \end{matrix}$ 4(24)

式中:σ _i为图10中局部放大图第i个单元成形结束时的应力值。

	Figure Option View Download New Window
	图10 工件应力分布示意图Fig.10 Distribution of stress on part

图11为4种成形方式与应力集中值 $\begin{matrix} \bar{σ} \end{matrix}$ 的对应关系。与多点拉形相比, 等速冲头主动加载、等时冲头主动加载、等差曲率冲头主动加载3种成形方式得到的应力集中值分别减小了11.1%、14.8%、9.5%。这是因为多点拉形时, 板料悬空区范围较大, 传力状态不稳定导致板料钳口处的应力集中严重。而另外3种冲头主动加载拉形, 成形时模具的所有冲头单元均与板料接触, 板料悬空区较小, 传力状态相对较稳定, 板料整体受力比较均匀, 钳口处的应力集中明显减小。所以改变多点冲头的主动加载路径, 能有效减小板料钳口处的应力集中, 提高板料的成形极限。

	Figure Option View Download New Window
	图11 成形方式与应力集中值的对应关系Fig.11 Relationship between forming method and stress concentration values

(2)不同加载路径对应力分布的影响

以下仅针对成形件成形区域的应力分布状况进行分析。为衡量应力分布, 定义了应力分布偏差量σ _c:

σ _c=σ _xt_max-σ _xt_min+σ _yt_max-σ _yt_min(25)

式中:σ _xt_max代表沿对称轴x方向t时刻分布的应力最大值; σ _xt_min代表沿对称轴x方向t时刻分布的应力最小值; σ _yt_max代表沿对称轴y方向t时刻分布的应力最大值; σ _yt_min代表沿对称轴y方向t时刻分布的应力最小值。

图12为在成形过程中应力分布偏差量随时间的变化。从图中可知, 在成形过程中, 不同加载路径拉形方式进行到相同时刻, 3种冲头主动加载路径拉形方式得到的应力分布偏差量均比多点拉形小。这是由于在整个成形过程中, 多点冲头主动加载路径的变化改变了板料的受力分布, 提高了板料受力的均匀性, 使应力分布更加均匀。

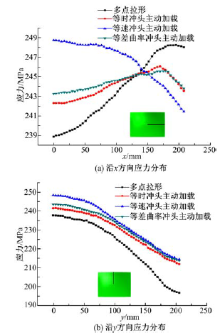
	Figure Option View Download New Window
	图12 应力偏差量随时间变化Fig.12 Value of stress deviations varying with time

图13为不同加载路径成形结束时, 成形件在对称轴上的应力分布。与多点拉形相比, 等差曲率冲头主动加载、等时冲头主动加载、等速冲头主动加载得到的应力分布偏差量分别减小了39.4%、28.6%、9.7%。这进一步说明, 改变多点冲头对板料的加载路径能够使应力分布更加均匀, 提高工件整体质量。

(3)不同加载路径对应变分布的影响

等效塑性应变能够体现金属在成形过程中的塑性积累情况, 为精确衡量应变分布, 定义了应变分布偏差量M:

M= $\begin{matrix} {(\overset{n_{x}}{\sum_{i = 1}} |ε_{xi} - {\bar{ε}}_{x}|)}^{2} \end{matrix}$ + $\begin{matrix} {(\overset{n_{y}}{\sum_{j = 1}} |ε_{yi} - {\bar{ε}}_{y}|)}^{2} \end{matrix}$ (26)

	Figure Option View Download New Window
	图13 应力沿对称轴的分布Fig.13 Distribution of stress on symmetry axis

式中:n_x为沿对称轴x方向提取的结点个数; n_y为沿对称轴y方向提取的结点个数; ε _xi为沿对称轴x方向成形结束时第i个结点处的应变值; ε _yi为沿对称轴y方向成形结束时第j个结点处的应变值; $\begin{matrix} {\bar{ε}}_{x} \end{matrix}$ = $\begin{matrix} \frac{\overset{n_{x}}{\sum_{i = 1}} ε_{xi}}{n_{x}} \end{matrix}$ ; $\begin{matrix} {\bar{ε}}_{y} \end{matrix}$ = $\begin{matrix} \frac{\overset{n_{y}}{\sum_{j = 1}} ε_{yi}}{n_{y}} \end{matrix}$ 。

图14为不同加载路径成形结束时成形件在对称轴上的应变分布。从图14可以看出, 等差曲率冲头主动加载和等时冲头主动加载得到的应变分布均匀性明显比多点拉形好。多点拉形、等时冲头主动加载、等速冲头主动加载、等差曲率冲头主动加载得到的应变分布偏差量M分别为 0.175、0.137、0.156、0.132。与多点拉形相比, 等时冲头主动加载、等速冲头主动加载、等差曲率冲头主动加载拉形得到的应变分布偏差量分别减小了21.7%、10.8%、24.6%。这是因为在拉形过程中, 通过主动改变多点冲头对板料的加载路径, 进而也改变了板料的变形路径, 改善了材料的整体受力状态, 使应力分布更加均匀, 应变也随之分布更加均匀, 提高了应变分布质量

	Figure Option View Download New Window
	图14 应变沿对称轴的分布Fig.14 Distribution of strain on symmetry axis

(4)不同加载路径对板料延伸率分布的影响

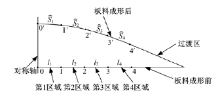
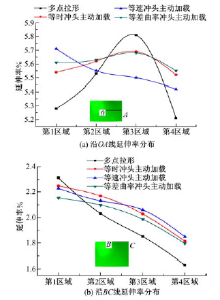
拉形过程中板料延伸率的分布对成形后工件的质量起着重要作用。由于拉形中材料延伸的方向主要是沿x轴方向, 因此针对板料x方向有效成形区域的延伸率分布进行分析。分别对板料成形前与成形结束时x方向上4个区域相应节点进行标记, 如图15所示, 成形前l₁、l₂、l₃、l₄长度相等, 成形结束时对应区域的弧长分别为 $\begin{matrix} {\overset{}{s}}_{1} \end{matrix}$ 、 $\begin{matrix} {\overset{}{s}}_{2} \end{matrix}$ 、 $\begin{matrix} {\overset{}{s}}_{3} \end{matrix}$ 、 $\begin{matrix} {\overset{}{s}}_{4} \end{matrix}$ , 求取各部分延伸率Δ ξ _i, 延伸率的表达式如下:

Δ ξ _i= $\begin{matrix} \frac{{\overset{}{s}}_{i} - l_{i}}{l_{i}} \end{matrix}$ (27)

	Figure Option View Download New Window
	图15 板料节点位置的变化Fig.15 Node position of sheet before and after forming

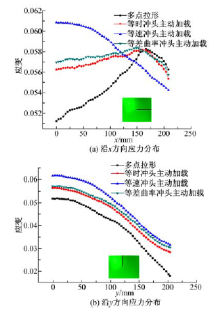
图16为不同加载路径对应的材料延伸率分布图, 其中OA、BC分别为成形件上具有代表性的两条成形线。从图16可以直观看出, 等差曲率冲头主动加载方式得到延伸率分布效果最好, 而多点拉形得到的延伸率分布效果最差。与多点拉形相比, 等差曲率冲头主动加载、等时冲头主动加载、等速冲头主动加载得到的成形件在OA线上的延伸率分布变化范围分别减小了69.2%、58.1%、48.6%, 在BC线上的变化范围分别减小了48.5%、44.1%、35.2%。这是由于在多点拉形过程中, 成形区板料的贴模有先后顺序, 先贴模部分和后贴模部分板料的变形量存在较大差异, 而在多点冲头主动加载拉形中, 成形区的板料一直处于贴模状态, 不存在先后贴模顺序, 成形区部分的板料变形差异较小, 材料整体流动比较均匀, 最终使得延伸率分布更加均匀。

	Figure Option View Download New Window
	图16 延伸率的分布Fig.16 Distribution of elongation

4 结论

(1)理论分析表明, 等差曲率冲头主动加载路径能够有效提高拉形过程中板料的受力均匀性。

(2)对比分析了不同加载路径对板料钳口处应力集中的影响, 模拟结果表明:与多点拉形相比, 等时冲头主动加载、等速冲头主动加载、等差曲率冲头主动加载拉形均能减小板料钳口处的应力集中, 减小百分比分别为11.1%、14.8%、9.5%。

(3)对比分析了不同加载路径对板料成形后的应力、应变及延伸率分布的影响。研究结果表明:与多点拉形相比, 设计的3种多点冲头主动加载路径方法均能提高应力、应变和延伸率分布均匀性; 其中等差曲率冲头主动加载路径对应力、应变分布均匀性提升效果最好, 分别提高了39.4%、24.6%, 变化趋势与理论分析结果相一致。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Tan Fu-xing, Li Ming-zhe, Cai Zhong-yi. Formability analysis on the process of multi-point forming for titanium alloy retiary sheet[J]. International Journal of Advanced Manufacturing Technology, 2009, 41(11): 1059-1065. [本文引用:1]
[2]	Philippe Dal Santo, Guénaël Germain, Serge Boude, et al. Cold forming by stretching of aeronautic sheet metal parts[J]. International Journal of Computer Integrated Manufacturing, 2014, 27(2): 344-351. [本文引用:1]
[3]	Kohara S. Forming limit curves of aluminum and aluminum alloy sheets and effects of strain path on thecurves[J]. Materials Processing Technology, 1993, 38(3): 723-735. [本文引用:1]
[4]	蔡中义, 张海明, 李光俊, 等. 多点拉形数值模拟及模具型面补偿方法[J]. 吉林大学学报: 工学版, 2008, 38(2): 329-333. Cai Zhong-yi, Zhang Hai-ming, Li Guang-jun, et al. Numerical simulation of sheet metal multi-point stretch forming and compensation of die surface[J]. Journal of Jilin University (Engineering Science), 2008, 38(2): 329-333. [本文引用:1]
[5]	周朝晖, 蔡中义, 李明哲. 多点模具的拉形工艺及其数值模拟[J]. 吉林大学学报: 工学版, 2005, 35(3): 287-291. Zhou Zhao-hui, Cai Zhong-yi, Li Ming-zhe. Stretching process based on multi-point die and its numerical simulation[J]. Journal of Jilin University (Engineering Science), 2005, 35(3): 287-291. [本文引用:1]
[6]	Li X J, Zhang Z Q, Zheng Q F, et al. A study of basic mechanics in the multi-point single-point incremental combined forming of sheets metal[J]. Materials ResearchInnovations, 2015, 19(5): 385-388. [本文引用:1]
[7]	陈雪, 李明哲, 付文智, 等. 基于多点模的板材柔性夹钳拉形夹持力[J]. 吉林大学学报: 工学版, 2011, 41(1): 95-99. Chen Xue, Li Ming-zhe, Fu Wen-zhi, et al. Clamping force of sheet metal flexible grippers stretch-forming based on multi-point die[J]. Journal of Jilin University (Engineering Science), 2011, 41(1): 95-99. [本文引用:1]
[8]	Wiebengaa J H, Atzemab E H, van den Boogaardc A H. Stretching the limits of forming processes by robust optimization: a numerical and experimental demon- strator[J]. Journal of Materials Processing Technology, 2015, 217(5): 345-355. [本文引用:1]
[9]	王丽丽, 李东升, 李小强, 等. 可重构柔性多点模具蒙皮拉形模面补偿算法[J]. 北京航空航天大学学报, 2011, 37(8): 1011-1015. Wang Li-li, Li Dong-sheng, Li Xiao-qiang, et al. Die-face compensation algorithm in stretch forming of aircraft skin over reconfigurable compliant tooling[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(8): 1011-1015. [本文引用:1]
[10]	张冬娟, 崔振山, 李玉强, 等. 平面应变板料拉弯成形回弹理论分析[J]. 工程力学, 2007, 24(7): 66-71. Zhang Dong-juan, Cui Zhen-shan, Li Yu-qiang, et al. Springback of sheet metal after plane strain Stretch-bending[J]. Engineering Mechanics, 2007, 24(7): 66-71. [本文引用:1]
[11]	Paulsen Frode, Welo Torgeir. Application of numerical simulation in the bending of aluminum-alloy profiles[J]. Journal of Materials Processing Technology, 1996, 58(2): 274-285. [本文引用:1]

2009

0.0

... 0 引言与传统蒙皮拉形相比,多点拉形中的拉形模具由一系列规则排列、高度可调的基本体组成,快速可调的模具型面能够用于不同零件的柔性拉形^[1,2,3,4] ...

2014

0.0

1993

0.0

2008

0.0

. 2008, 38(2):329-333

Numerical simulation of sheet metal multi-point stretch forming and compensation of die surface

多点拉形数值模拟及模具型面补偿方法

Cai Zhong-yi , Zhang Hai-ming , Li Guang-jun

蔡中义, 张海明, 李光俊

摘　要：建立了板料多点拉形有限元模型，确立了用于动态显式算法的拉形加载模式，并应用到典型件的拉形过程数值模拟中。对马鞍形曲面件的多点拉形进行了数值模拟，探讨了成形件上应力、厚度等的分布规律以及回弹和弹性垫的不均匀变形对成形件精度的影响。模拟结果表明，成形件的应力、厚度分布均匀，卸载回弹很小，弹性垫的不均匀变形对成形件精度的影响比回弹要大；为获得精确形状的成形件，提出了一种基于数值模拟结果通过反复修正获得准确的多点拉形模具型面来补偿多点拉形中弹性垫的不均匀变形和回弹的方法。

2005

0.0

. 2005, 35(3):287-291

Stretching process based on multi-point die and its numerical simulation

多点模具的拉形工艺及其数值模拟

Zhou Zhao-hui , Cai Zhong-yi , Li Ming-zhe.

周朝晖, 蔡中义, 李明哲

... 这种成形方式能够节省模具制造成本,缩短零件制造周期,但多点拉形与传统拉形存在相同的局限性,由于传力区与拉形模不接触,板料与模具表面之间没有摩擦,毛料易变薄,夹头处应力集中较严重,零件成形后应力和应变分布均匀性有待进一步提高^[5,6,7,8,9] ...

2015

0.0

2011

0.0

. 2011, 41(1):95-99

Clamping force of sheet metal flexible grippers stretch-forming based on multi-point die

基于多点模的板材柔性夹钳拉形夹持力

Chen Xue , Li Ming-zhe , Fu Wen-zhi

陈雪, 李明哲, 付文智

The technology of sheet metal flexible grippers stretch forming (FGSF) was introduced briefly, theoretic formula and calculation method of clamping force were given. A finite element model was established, and the numerical simulations of FGSF based on multipoint die were performed by a dynamic explicit algorithm for the cylindrical, spherical and saddle surface of different material with different thickness. The variation histories of the clamping force and its influencing factors were analyzed. The results indicate that the material and sheet metal thickness are very sensitive to the clamping force during sheet stretch forming, and the relatively large clamping force is needed if material is stiffer and sheet metal is thicker. The clamping force for forming workpiece of double curvature is obviously larger than that for forming workpiece of single curvature. The obtained results are significant for the optimal design of sheet metal FGSF equipments and the study of sheet metal practical forming process.

简单介绍了板材柔性夹钳拉形（FGSF）工艺，提出了其夹持力的理论模型和计算方法。建立了有限元模型，采用动态显式算法对不同材料、不同板厚的圆柱面、球形面及马鞍面的基于多点模的FGSF过程进行了数值模拟，分析了夹持力的变化及影响因素。模拟结果表明：材料和板厚对工件拉形时夹持力的影响非常敏感，较硬、较厚的板材拉形时需要较大的夹持力；双曲率工件成形时所需的夹持力明显大于单曲率工件。本文研究结果对板材柔性夹钳拉形装置的结构优化设计与实际板材拉形工艺的研究都有重要的参考价值。

2015

0.0

2011

0.0

. 2011, 37(8):1011-1015

Die-face compensation algorithm in stretch forming of aircraft skin over reconfigurable compliant tooling

可重构柔性多点模具蒙皮拉形模面补偿算法

Wang Li-li , Li Dong-sheng , Li Xiao-qiang

王丽丽, 李东升, 李小强

2007

0.0

. 2007, 24(7):66-71 DOI:doi:10.3969/j.issn.1000-4750.2007.07.012

Springback of sheet metal after plane strain Stretch-bending

平面应变板料拉弯成形回弹理论分析

Zhang Dong-juan , Cui Zhen-shan , Li Yu-qiang

张冬娟, 崔振山, 李玉强

基于平面应变假设,采用服从Hill平方屈服准则和指数强化材料模型,建立了板料拉弯成形回弹量预测的理论模型.应用该模型计算了一个拉弯成形回弹实例,分析了单位宽度切向拉力、凸模圆角半径、摩擦因数及各向异性参数对板料回弹量的影响.分析结果表明,只有当中性层偏移距离超过板厚的四分之一时,增大切向拉力才能有效地控制板料回弹量,而且弯曲半径越大,增大切向拉力控制板料的回弹量越为有效,然而拉力不能无限制的增大,它的计算准则为板料最外层的等效应变应不大于极限应变.同时还表明,摩擦因数对板料回弹量的影响随切向拉力的增大变得更为显著,而各向异性参数对板料拉弯成形回弹量的影响也较为明显.与有限元数值模拟预测结果的对比表明,理论模型预测板料拉弯成形回弹量与有限元数值模拟结果很接近.

... ③板料不可压缩,弯曲过程中板料纵向纤维之间无挤压,即认为板料厚向应力为零^[10,11] ...

1996

0.0

... ③板料不可压缩,弯曲过程中板料纵向纤维之间无挤压,即认为板料厚向应力为零^[10,11] ...