基于离散事件触发通信机制的非均匀传输网络化控制系统故障调节与通信满意协同设计

引用本文

李炜, 李亚洁. 基于离散事件触发通信机制的非均匀传输网络化控制系统故障调节与通信满意协同设计[J].吉林大学学报（工学版）, 2018,48(1): 245-258
LI Wei, LI Ya-jie. Satisfactory integrated design between failure accommodation and communication for non-uniform transmission networked control system under discrete event-triggered communication scheme[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 245-258 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161083
Permissions

基于离散事件触发通信机制的非均匀传输网络化控制系统故障调节与通信满意协同设计

李炜¹, 李亚洁^1,²

1. 兰州理工大学电气工程与信息工程学院, 兰州730050

2.中国石油兰州石化公司自动化研究院,兰州730060

通讯作者：李亚洁(1981-),女,博士研究生.研究方向:动态系统容错控制.E-mail:lyajie@petrochina.com.cn

作者简介:李炜(1963-),女,教授,博士生导师.研究方向:动态系统故障诊断与容错控制.E-mail:liwei@lut.cn

基金:国家自然科学基本项目(61364011,61463030); 甘肃省自然科学基金项目(1610RJYA013)

摘要

基于离散事件触发通信机制(DETCS),考虑执行器饱和约束,研究了网络化控制系统(NCS)同时满足多项约束目标的主动容错与网络通信间的协同设计问题。首先,通过在传统的NCS中引入事件发生器,提出并构建了DETCS下NCS主动容错的架构与设计理念,即基于系统中物理采样器采样周期的驱动来设计状态和故障观测器,基于网络通信约束触发的事件驱动来设计反馈控制。其次,建立了集网络属性、执行器饱和约束、故障估计、扰动信息、故障调节与反馈控制为一体的非均匀传输闭环故障系统模型。接着,给出了满足 H_∞性能的状态和时变故障估计的广义观测器的求解方法,并以此为基础给出了非均匀传输故障调节与网络通信间的满意协同设计方法。最后,通过采用四容水箱基准实例验证了理论结果的正确性与实用性。

关键词: 通信技术; 时变故障调节; 非均匀传输; 满意主动容错控制; 执行器饱和; 协同设计

中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2018)01-0245-14

Satisfactory integrated design between failure accommodation and communication for non-uniform transmission networked control system under discrete event-triggered communication scheme

LI Wei¹, LI Ya-jie^1,²

1. College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050,China

2. Institute of Automation,Lanzhou Petrochemical Company of CNPC, Lanzhou 730060, China

Abstract

Based on the Discrete Event-triggered Communication Scheme (DETCS) and considering actuator saturation constraint, the co-design problem was studied for Network Control System (NCS). Such co-design was between active fault-tolerant control with multi-objective constraints and network communication. First, the NCS active fault-tolerant framework and design concept were proposed by introducing event-trigger to the traditional NCS, namely, the observer of state and fault was driven by equal physical sampling period of the system, and the feedback control was driven by event with communication constraints. Second, the model of non-uniform transmission closed-loop failure system was established dedicatedly, which integrated network attribute, actuator saturation constraint, estimation value of failure, and disturbance information into one uniform framework. Third, the solving method of state and fault estimation with H_∞- performance was proposed based on generated observer. The co-design method between satisfactory failure accommodation and network communication was given for non-uniform transmission NCS. Finally, simulation experiment was conducted to verify the effectiveness and feasibility of the proposed method by a four tank benchmark example.

Keyword: communication technology; time-varying failure accommodation; non-uniform transmission; satisfactory active fault-tolerant control; actuator saturation; co-design

Show Figures

0 引言

随着现代网络化控制系统(Networked control systems, NCS)超复杂性和大规模性的日益突显, 安全可靠性已经成为保证NCS正常运行的一项重要需求, 这也促使了近几年来学术界对NCS的故障诊断与容错控制类问题的高度关注^{[1, 2, 3]}, 并取得了卓有成效的进展^{[4, 5]}。在已取得的容错控制研究成果中绝大多数文献是基于周期时间触发通信机制(Periodic time-triggered communication scheme, PTTCS )来完成系统的分析与设计的。PTTCS在设计系统时具有简单易用、设计便捷等优势, 但是该机制却存在一些诸如浪费网络资源、割裂NCS的控制与通信设计等不足。近期, 有学者将一种新型的通信机制— — 离散事件触发通信机制 (Discrete event-triggered communication scheme, DETCS)^{[6, 7, 8]}, 引入到了NCS的容错控制中^{[9, 10, 11]}, 并取得了良好的应用效果。与PTTCS不同的是, DETCS只在离散时刻点发送满足事件触发条件的系统数据。考虑传感器和执行器的故障概率, 文献[9]在DETCS下研究了NCS的可靠性控制问题。在DETCS下, 文献[10]对具有执行器饱和约束的参数不确定非线性NCS进行了鲁棒容错控制问题的研究。然而, 基于DETCS研究NCS容错控制的成果几乎都集中在被动容错控制方面, 针对主动容错控制的相关研究还少有涉及。在实际应用中, 主动容错控制在处理不同类型故障时不仅具有灵活性高与性能更优等特点, 而且其控制器设计的保守性也要明显小于被动容错的情形^{[12, 13]}。因而, 在DETCS下研究NCS的主动容错控制与通信间的协同设计问题, 对于提高NCS的容错性能, 实现NCS容错性能与通信资源占用之间的协同兼顾, 都具有重要意义。

随着数字计算机技术的迅速发展, 微处理器被广泛应用于各个工业领域, 然而, 在这种情形下, 整个控制系统的被控对象是连续的而控制律是离散的, 此类系统即为采样数据系统。当将DETCS引入至传统的NCS中时, 满足事件发生器筛选条件的系统数据又将以非均匀周期的方式经由网络进行传输。由于非均匀传输周期的大小均为采样周期的整数倍, 则可以将采样器与事件发生器合并看作为一个虚拟的非均匀采样器, 因而可以采用非均匀采样系统的相关理论研究DETCS下NCS的非均匀传输问题。采样系统的研究方法主要有3类^[14]:一是先对连续对象进行离散化, 应用离散系统控制理论进行系统设计; 二是根据连续系统的理论设计出连续控制器, 然后再将其离散化; 三是将非均匀采样周期对系统的影响转化为对系统时滞的影响, 应用时滞系统中成熟的理论^[15]研究此类问题。其中, 第三类方法因无需对连续的系统对象进行离散化, 也无需对控制器进行特殊处理, 受到了较多的关注^[16], 但其保守性亦是不可忽视的问题。

仅从容错控制系统的性能而言, NCS不仅需要保证故障系统具有最基本的稳定性能, 还需要系统具有一些其他的良好动态性能^{[17, 18]}(如α -稳定性, H_∞-性能, H₂-性能等)。文献[18]推证出了NCS同时满足多种性能指标的满意容错控制器的求解方法。在控制系统中, 执行器所受到的饱和约束对系统的影响亦是不容忽视的^{[19, 20]}。文献[20]指出执行器饱和是导致系统性能下降甚至失稳的重要诱因, 因此, 在实际系统的设计中, 更应从工程应用层面考虑执行器饱和约束对系统性能的影响。

受上述问题激发, 基于非均匀采样系统的理论分析非均匀传输问题这一思想, 本文在DETCS下研究了非均匀传输NCS的主动容错控制与通信满意协同设计问题, 这里的主动容错控制包括连续时变故障估计、DETCS下故障调节与通信满意协同设计两部分内容。对执行器时变故障的估计是通过采用观测器获得的, 而满意协同设计是指实现故障调节与网络通信间的相互协同, 同时满足不同的控制性能指标和网络通信资源占用指标, 以达到满意的控制效果和资源占用率。

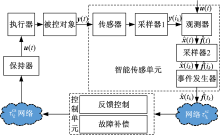
1 DETCS下网络化主动容错控制系统描述

1.1 NCS主动容错框架描述

为了克服PTTCS中网络资源浪费问题和解决NCS中控制与通信的协同设计问题, 首先将DETCS引入至传统的NCS中, 并在DETCS中研究非均匀传输NCS时变故障调节与通信的满意协同设计问题, 系统结构如图1所示。

	Figure Option View Download New Window
	图1 DETCS下非均匀传输NCS主动容错控制框架Fig.1 Active fault-tolerant control framework of uniform transmission under DETCS

从图1中可以看出, DETCS下NCS主动容错控制的框架中主要包括被控对象、智能传感、反馈控制、故障补偿、保持、执行等相关功能单元。与PTTCS下的主动容错控制系统架构相比, 为了节省通信网络资源, 由观测器输出的估计信息需要经过事件发生器进行筛选; 为了不因DETCS的引入而影响故障估计的精准性与及时性, 将事件发生器置于观测器之后, 且观测器的功能由智能传感单元的CPU来实现。

1.2 被控对象描述

选取一类典型的具有执行器饱和约束与时变故障的NCS受控对象模型如下:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{x} (t) = Ax (t) + Bsat (u (t)) + E_{d} d (t) + E_{f} f (t) \\ y (i_{k}) = Cx (i_{k}) + D_{v} v (i_{k}) \end{matrix} \end{matrix}$ (1)

式中:x(t)∈ Rⁿ、u(t)∈ $\begin{matrix} R^{n_{u}} \end{matrix}$ 分别为系统的状态向量和控制向量; d(t)∈ $\begin{matrix} R^{n_{d}} \end{matrix}$ 为系统中的扰动; y(i_k)∈ R^m、v(i_k)∈ $\begin{matrix} R^{n_{v}} \end{matrix}$ 分别为系统的采样输出量和离散测量扰动, 其中{i₁, i₂, …, i_k, …}表示系统中物理采样器的采样时刻序列; f(t)∈ $\begin{matrix} R^{n_{f}} \end{matrix}$ 为未知的连续时变故障, 其导数被假设是范数有界的, 即存在一个常数f₀且|| $\begin{matrix} \overset{\cdot}{f} \end{matrix}$ (t) ||≤ f₀; 函数sat(· ):R^m→ R^m是一个标准的多变量饱和函数, sat(u)= $\begin{matrix} [sat (u_{1}), sat (u_{2}), \dots, sat (u_{m} {)]}^{T} \end{matrix}$ , 其中, sat(u_i)=sign(u_i)min{1, |u_i|}; A∈ R^{n× n}、B∈ $\begin{matrix} R^{n \times n_{u}} \end{matrix}$ 、E_d∈ $\begin{matrix} R^{n \times n_{d}} \end{matrix}$ 、E_f∈ $\begin{matrix} R^{n \times n_{f}} \end{matrix}$ 、C∈ R^{n× n}、D_v∈ $\begin{matrix} R^{n \times n_{v}} \end{matrix}$ 分别表示系统矩阵、输入矩阵、状态扰动矩阵、故障系数矩阵、系统输出矩阵以及输出扰动矩阵。

1.3 观测器与事件发生器

在图1中, 采样器1、2受时钟驱动进行同步采样, 其采样周期均为h; 事件发生器和执行器均由事件来驱动。智能传感单元包含了传感变送、采样保持、数字观测器和事件发生器。可以看到:经由智能传感单元, 采样器1输出的信号为等物理周期的离散信号, 由于在一个采样周期中信号的幅值保持不变, 则在相邻的采样时刻间可借助于时滞系统理论^[15]为采样数据NCS(1)设计状态和故障观测器。通过将采样周期转换为时滞, 便可得到一个连续时变的时滞输出:

y(t)=Cx(t-τ ₁(t))(2)

式中:τ ₁(t)=t-i_k, i_k≤ t< i_k+₁, 0< τ ₁(t) ≤ h_τ=h。

当t∈ [i_k, i_k+₁)时, 构造一个状态观测器:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{\dot{x}} (t) = A \dot{x} (t) + Bsat (u (t)) + E_{f} \dot{f} (t) \\ - L (\dot{y} (t) - y (t)) \\ \dot{y} (t) = C \dot{x} (t - τ_{1} (t)) \end{matrix} \end{matrix}$ (3)

定义e_x(t)= $\begin{matrix} \dot{x} \end{matrix}$ (t)-x(t); e_y(t)= $\begin{matrix} \dot{y} \end{matrix}$ (t)-y(t); e_f(t)= $\begin{matrix} \dot{f} \end{matrix}$ (t)-f(t)。

注1:当t∈ [i_k, i_k+₁)时, 受y(i_k)与u(t)在一个采样周期h内保持不变的影响, 观测器的输出 $\begin{matrix} \dot{x} \end{matrix}$ (t)和 $\begin{matrix} \dot{f} \end{matrix}$ (t)在一个采样周期h内同样保持不变, 且在对应的采样时刻i_k有, $\begin{matrix} \dot{x} \end{matrix}$ (i_k)= $\begin{matrix} \dot{x} \end{matrix}$ (t), $\begin{matrix} \dot{f} \end{matrix}$ (i_k)= $\begin{matrix} \dot{f} \end{matrix}$ (t)。为了便于之后事件发生器进行数据筛选, 图1应用采样器2在离散时刻点i_k进行故障估计与状态估计的取值。采样器1与采样器2均由同一时钟且同样的采样周期h来驱动, 二者之间不存在异步问题。

图1中, 从观测器输出值中被取样的估计信息 $\begin{matrix} \dot{x} \end{matrix}$ (i_k)和 $\begin{matrix} \dot{f} \end{matrix}$ (i_k), 在经网络传输至控制器之前将经过一个事件发生器, 其功能在于筛选出满足某种特定的数据并发送至容错控制器。文中采用的事件触发条件为

[ $\begin{matrix} \dot{x} \end{matrix}$ (i_k)- $\begin{matrix} \dot{x} \end{matrix}$ (t_k)]^TΦ [ $\begin{matrix} \dot{x} \end{matrix}$ (i_k)- $\begin{matrix} \dot{x} \end{matrix}$ (t_k)]≤

δ $\begin{matrix} {\dot{x}}^{T} \end{matrix}$ (t_k)Φ $\begin{matrix} \dot{x} \end{matrix}$ (t_k) (4)

式中:Φ 为待设计的正定对称矩阵; δ > 0为一个预先给定的事件触发参数; 假设序列 $\begin{matrix} \{t_{k}\} \end{matrix}$ {k=0, 1, 2, …}为事件发生器后端的发送时刻序列; $\begin{matrix} \dot{x} \end{matrix}$ (t_k)表示观测器后端在上一时刻通过事件发生器计算比较且满足触发条件后而传输的最新的状态估计值。

注2:故障的估计值 $\begin{matrix} \dot{f} \end{matrix}$ (t_k)同样是需要通过网络进行传输的, 但并不是所有的故障估计值均通过网络进行传输。而是在系统中建立了一种联动的数据传输机制, 只有当状态估计值 $\begin{matrix} \dot{x} \end{matrix}$ (t_k)满足事件发生器中的触发条件(4)时, 与之对应的故障估计值 $\begin{matrix} \dot{f} \end{matrix}$ (t_k)才会经网络进行传输。当状态估计值 $\begin{matrix} \dot{x} \end{matrix}$ (t_k)不满足事件发生器中的触发条件(4)时, 与之对应的故障估计值 $\begin{matrix} \dot{f} \end{matrix}$ (t_k)将不会经网络进行传输, 因此并不会增大通信资源的消耗。

1.4 DETCS下传输时延的分析描述

在NCS中, t_k时刻经网络传输的数据要经过一定的网络传输时延 $\begin{matrix} τ_{t_{k}} \end{matrix}$ 才能被传输至执行器端, 其中, $\begin{matrix} τ_{t_{k}} \end{matrix}$ = $\begin{matrix} τ_{sc}^{t_{k}} \end{matrix}$ + $\begin{matrix} τ_{c}^{t_{k}} \end{matrix}$ + $\begin{matrix} τ_{ca}^{t_{k}} \end{matrix}$ , $\begin{matrix} τ_{sc}^{t_{k}} \end{matrix}$ 为t_k时刻存在于智能传感单元与控制单元间的网络传输时延, $\begin{matrix} τ_{c}^{t_{k}} \end{matrix}$ 为t_k时刻存在于控制单元中的计算时延, $\begin{matrix} τ_{ca}^{t_{k}} \end{matrix}$ 为t_k时刻存在于控制单元与保持器之间的网络传输时延; { $\begin{matrix} {\overset{̅}{t}}_{k} \end{matrix}$ = t_k+ $\begin{matrix} τ_{sc}^{t_{k}} \end{matrix}$ + $\begin{matrix} τ_{c}^{t_{k}} \end{matrix}$ }(k=0, 1, 2, …)为控制单元后端的数据更新时刻序列, { $\begin{matrix} {\dot{t}}_{k} \end{matrix}$ =t_k+ $\begin{matrix} τ_{sc}^{t_{k}} \end{matrix}$ + $\begin{matrix} τ_{c}^{t_{k}} \end{matrix}$ + $\begin{matrix} τ_{ca}^{t_{k}} \end{matrix}$ }(k=0, 1, 2, …)为保持器前端的数据更新时刻序列。

在事件发生器之后, 针对任意一个传输区间[t_k, t_k+₁), 显然有 $\begin{matrix} \cup_{k}^{=} \end{matrix}$ [t_k, t_k+₁)=[0, ∞ )。将事件发生器后端的数据发送周期记为h_k, 则有h_k=t_k+₁-t_k, 此时, 观测器后的估计信息是按照非均匀周期被传输的。在考虑时延的情况下, 当u( $\begin{matrix} {\dot{t}}_{k} \end{matrix}$ )已送达到保持器而u( $\begin{matrix} {\dot{t}}_{k + 1} \end{matrix}$ )未送达至保持器时, 考虑时延的任意一个传输区间可定义为:

Ω =[t_k+ $\begin{matrix} τ_{t_{k}} \end{matrix}$ , t_k+₁+ $\begin{matrix} τ_{t_{k + 1}} \end{matrix}$ )(5)

可将传输区间剖分成若干个子区间:

Ω = $\begin{matrix} Δ_{k}^{0} \end{matrix}$ ∪ … $\begin{matrix} Δ_{k}^{l_{k}} \end{matrix}$ ∪ …∪ $\begin{matrix} Δ_{k}^{d_{k}} \end{matrix}$ (6)

式中: $\begin{matrix} Δ_{k}^{l_{k}} \end{matrix}$ =[t_k+l_kh+ $\begin{matrix} τ_{t_{k} + l_{k} h} \end{matrix}$ , t_k+(l_k+1)h+ $\begin{matrix} τ_{t_{k} + (l_{k} + 1) h} \end{matrix}$ ); l_k=0, 1, 2, …, d_k; d_kh=t_k+₁-t_k-h。在采样时刻 $\begin{matrix} t_{k + l_{k} h} \end{matrix}$ , 假设 $\begin{matrix} τ_{t_{k} + l_{k} h} \end{matrix}$ 为网络传输时延。

当t∈ $\begin{matrix} Δ_{k}^{l_{k}} \end{matrix}$ 时, 定义网络传输时延函数τ ₂(t)为

τ ₂(t)=t-t_k(7)

由式(6)(7)可得网络传输时延函数τ ₂(t)的上、下界为:

0< l_kh+ $\begin{matrix} τ_{t_{k} + l_{k} h} \end{matrix}$ ≤ τ ₂(t)≤ (l_k+1)h+

$\begin{matrix} τ_{t_{k} + (l_{k} + 1) h} \end{matrix}$ ≤ (d_k+1)h+ $\begin{matrix} τ_{t_{k} + (l_{k} + 1) h} \end{matrix}$ =t_k+₁-

t_k+ $\begin{matrix} τ_{t_{k} + (l_{k} + 1) h} \end{matrix}$ ≤ h_max_k+ $\begin{matrix} \overset{̅}{τ} \end{matrix}$ (8)

式中:定义 $\begin{matrix} \overset{̅}{h} \end{matrix}$ =h_max_k+ $\begin{matrix} \overset{̅}{τ} \end{matrix}$ =h_max_k+max{ $\begin{matrix} τ_{t_{k + (l_{k} + 1) h_{2}}} \end{matrix}$ }。

当t∈ $\begin{matrix} Δ_{k}^{l_{k}} \end{matrix}$ , 定义最新采样时刻与最新发送时刻状态估计值间的差值 $\begin{matrix} \dot{e} \end{matrix}$ (i_k)为:

$\begin{matrix} \dot{e} \end{matrix}$ (i_k)= $\begin{matrix} \dot{x} \end{matrix}$ (i_k)- $\begin{matrix} \dot{x} \end{matrix}$ (t_k)(9)

离散事件触发条件为:

$\begin{matrix} {\dot{e}}^{T} \end{matrix}$ (i_k)Φ $\begin{matrix} \dot{e} \end{matrix}$ (i_k)≤ δ $\begin{matrix} {\dot{x}}^{T} \end{matrix}$ (t-τ ₂(t))Φ $\begin{matrix} \dot{x} \end{matrix}$ (t-τ ₂(t))(10)

注3:状态、故障的估计以及传输数据的筛选, 均由智能传感单元完成, 优点如下:一是故障估计时经过物理采样器可以得到更完整的数据, 使得故障的估计可以更精准及时; 二是充分采用了NCS中各智能体的计算功能, 并通过事件发生器从采样数据中筛选出传输数据, 减轻了网络及控制器CPU的计算负担。

1.5 闭环故障NCS模型的建立

假设存在矩阵B⁺∈ $\begin{matrix} R^{n_{u} \times n} \end{matrix}$ , 满足(I-BB⁺)E_f=0, 即rank(B, E_f)=rank(B)。考虑时延、事件发生器等因素的影响, 控制单元的数据信息是以非均匀的方式进行更新的, 采用如下非均匀传输的状态反馈和故障调节主动容错控制器:

u(t)=-K $\begin{matrix} \dot{x} \end{matrix}$ (t_k)-B⁺E_f $\begin{matrix} \dot{f} \end{matrix}$ (t_k) (11)

t∈ [t_k+ $\begin{matrix} τ_{t_{k}} \end{matrix}$ , t_k+₁+ $\begin{matrix} τ_{t_{k + 1}} \end{matrix}$ )

式中:K∈ $\begin{matrix} R^{n_{u} \times n} \end{matrix}$ 为待设计的控制器增益矩阵, 综合由式(1)(7)及(11)可得:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{x} (t) = Ax (t) - Bsat (K (\dot{x} (t - τ_{1} (t)) - \dot{e} (t - \\ τ_{2} (t))) - Bsat (K e_{x} (t - τ_{2} (t)) - E_{f} e_{f} (t - \\ τ_{2} (t)) + τ_{2} (t) E_{f} \overset{\cdot}{f} (t) + E_{d} d (t) \\ y (t_{k}) = Cx (t_{k}) + Dv (t_{k}) \end{matrix} \end{matrix}$ (12)

注4:闭环故障NCS(12)将网络属性、执行器饱和约束、故障估计信息、扰动信息特别是事件触发信息 $\begin{matrix} \dot{e} \end{matrix}$ (t-τ ₂(t))集成在了同一个模型中, 这为之后的协同求解状态反馈控制器K、故障调节器B⁺和事件触发权矩阵Φ 奠定了基础, 使主动容错控制与通信的协同设计成为了可能。

2 基于广义状态观测器的时变故障及状态估计

基于式(3)和相关定义, 则有误差系统为:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{e}}_{x} (t) = A e_{x} (t) + E_{f} e_{f} (t) - E_{d} d (t) - \\ LC e_{x} (t - τ_{1} (t)) + L D_{v} v (t - τ_{1} (t)) \\ e_{y} (t) = C e_{x} (t - τ_{1} (t)) - D_{v} v (t - τ_{1} (t)) \end{matrix} \end{matrix}$ (13)

为了估计出连续时变故障, 可以将e_x(t)与e_f(t)增广成一个整体进行设计, 首先采用如下故障估计算法:

$\begin{matrix} \overset{\cdot}{\dot{f}} \end{matrix}$ (t)=-Fe_y(t)(14)

根据式(14), 故障估计的误差对时间的导数可写作:

$\begin{matrix} {\overset{\cdot}{e}}_{f} \end{matrix}$ (t)=-FCe_x(t-τ ₁(t))+FD_vv(t-τ ₁(t))- $\begin{matrix} \overset{\cdot}{f} \end{matrix}$ (t) (15)

则状态估计误差和故障估计误差的增广模型为:

$\begin{matrix} \overset{\cdot}{\overset{̅}{e}} \end{matrix}$ (t)= $\begin{matrix} \overset{̅}{A} \end{matrix} \begin{matrix} \overset{̅}{e} \end{matrix}$ (t)- $\begin{matrix} \overset{̅}{L} \end{matrix} \begin{matrix} \overset{̅}{C} \end{matrix} \begin{matrix} \overset{̅}{e} \end{matrix}$ (t-τ ₁(t))+ $\begin{matrix} {\overset{̅}{E}}_{d} \end{matrix}$ d(t)+

$\begin{matrix} \overset{̅}{L} \end{matrix}$ D_vv(t-τ ₁(t)) (16)

式中: $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t)= $\begin{matrix} [\begin{matrix} e_{x} (t) \\ e_{f} (t) \end{matrix}] \end{matrix}$ ; $\begin{matrix} \overset{̅}{d} \end{matrix}$ (t)= $\begin{matrix} [\begin{matrix} d (t) \\ \overset{\cdot}{f} (t) \end{matrix}] \end{matrix}$ ; $\begin{matrix} \overset{̅}{A} \end{matrix}$ = $\begin{matrix} [\begin{matrix} A & E_{f} \\ 0 & 0 \end{matrix}] \end{matrix}$ ; $\begin{matrix} {\overset{̅}{E}}_{d} \end{matrix}$ = $\begin{matrix} [\begin{matrix} E_{d} & 0 \\ 0 & I \end{matrix}] \end{matrix}$ , $\begin{matrix} \overset{̅}{L} \end{matrix}$ = $\begin{matrix} [\begin{matrix} L \\ F \end{matrix}] \end{matrix}$ , $\begin{matrix} \overset{̅}{C} \end{matrix}$ =[C 0]。

故障估计与状态估计的设计目标:针对采样数据NCS(1), 寻求鲁棒广义观测器的增益矩阵 $\begin{matrix} \overset{̅}{L} \end{matrix}$ , 使得误差系统(16)能够保持渐近稳定, 并使得扰动d(t)和测量扰动v(i_k)满足最优的H_∞性能指标|| $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t)|| $\begin{matrix} _{2}^{2} \end{matrix}$ ≤ $\begin{matrix} γ_{1}^{2} \end{matrix}$ (||d(t)|| $\begin{matrix} _{2}^{2} \end{matrix}$ + $\begin{matrix} \overset{\infty}{\sum_{k = 0}} \end{matrix}$ (i_k+₁-i_k)||v(i_k)|| $\begin{matrix} _{2}^{2} \end{matrix}$ )。

定理1 针对于采样数据NCS(1), 当采用观测器(3)和故障估计器(14)时, 如果存在正定矩阵P> 0、Q> 0、S> 0、R> 0以及矩阵N、Z满足:

$\begin{matrix} \{\begin{matrix} \min γ_{1} s.t. (17) ~ (18) \\ [\begin{matrix} Π_{11}^{(1)} & Π_{12}^{(1)} & Π_{13}^{(1)} & Π_{14}^{(1)} & 0 \\ * & Π_{22}^{(1)} & Π_{23}^{(1)} & Π_{24}^{(1)} & Π_{25}^{(1)} \\ * & * & Π_{33}^{(1)} & Π_{34}^{(1)} & 0 \\ * & * & * & - γ_{1}^{2} I & Π_{45}^{(1)} \\ * & * & * & * & - h_{τ} n_{1} P \end{matrix}] < 0 \\ [\begin{matrix} Π_{11}^{(2)} & Π_{12}^{(2)} & {\bar{PE}}_{d} & Y D_{v} \\ * & Π_{22}^{(2)} & 0 & 0 \\ * & * & - γ_{1}^{2} I & 0 \\ * & * & * & - γ_{1}^{2} I \end{matrix}] < 0 \end{matrix} \end{matrix}$ (17)

$\begin{matrix} [\begin{matrix} R & N^{T} \\ * & Z \end{matrix}] \end{matrix}$ > 0 (18)

则可以使得状态估计误差e_x(t)和时变故障估计误差e_f(t)保持渐近收敛, 并满足最优H_∞性能指标 $\begin{matrix} = \overset{̅}{e} =_{2}^{2} \end{matrix}$ ≤ $\begin{matrix} γ_{1}^{2} \end{matrix}$ ( $\begin{matrix} = d (t) =_{2}^{2} \end{matrix}$ + $\begin{matrix} \overset{\infty}{\sum_{k = 0}} \end{matrix}$ (i_k+₁-r_k) $\begin{matrix} = v (i_{k}) =_{2}^{2} \end{matrix}$ ), 其中:

$\begin{matrix} Π_{11}^{(1)} \end{matrix}$ =P $\begin{matrix} \overset{̅}{A} \end{matrix}$ + $\begin{matrix} {\overset{̅}{A}}^{T} \end{matrix}$ P-n₂P+I+N₁+ $\begin{matrix} {N^{T}}_{1} \end{matrix}$ +h_τn₁ $\begin{matrix} {\overset{̅}{A}}^{T} \end{matrix}$ P $\begin{matrix} \overset{̅}{A} \end{matrix}$ +h_τn₂(P $\begin{matrix} \overset{̅}{A} \end{matrix}$ + $\begin{matrix} {\overset{̅}{A}}^{T} \end{matrix}$ P)

$\begin{matrix} Π_{12}^{(1)} \end{matrix}$ =-Y $\begin{matrix} \overset{̅}{C} \end{matrix}$ +n₂P-N₁+ $\begin{matrix} {N^{T}}_{2} \end{matrix}$ -h_τn₁ $\begin{matrix} {\overset{̅}{A}}^{T} \end{matrix}$ Y $\begin{matrix} \overset{̅}{C} \end{matrix}$ -h_τn₂Y $\begin{matrix} \overset{̅}{C} \end{matrix}$ -h_τn₂ $\begin{matrix} {\overset{̅}{A}}^{T} \end{matrix}$ P

$\begin{matrix} Π_{13}^{(1)} \end{matrix}$ =P $\begin{matrix} {\overset{̅}{E}}_{d} \end{matrix}$ +h_τn₁ $\begin{matrix} {\overset{̅}{A}}^{T} \end{matrix}$ P $\begin{matrix} {\overset{̅}{E}}_{d} \end{matrix}$ +h_τn₂P $\begin{matrix} {\overset{̅}{E}}_{d}^{} \end{matrix}$

$\begin{matrix} Π_{14}^{(1)} \end{matrix}$ =YD_v+h_τn₁ $\begin{matrix} {\overset{̅}{A}}^{T} \end{matrix}$ YD_v+h_τn₂YD_v

$\begin{matrix} Π_{22}^{(1)} \end{matrix}$ =-h_τn₃P-n₂P-N₂- $\begin{matrix} {N^{T}}_{2} \end{matrix}$ +h_τn₂Y $\begin{matrix} \overset{̅}{C} \end{matrix}$ +

h_τn₂ $\begin{matrix} {\overset{̅}{C}}^{T} \end{matrix}$ Y^T+2n₃h_τP

$\begin{matrix} Π_{23}^{(1)} \end{matrix}$ =-h_τn₁ $\begin{matrix} {\overset{̅}{C}}^{T} \end{matrix}$ Y^T $\begin{matrix} {\bar{E}}^{T}_{d} \end{matrix}$ -h_τn₂P $\begin{matrix} {\overset{̅}{E}}_{d}^{} \end{matrix}$

$\begin{matrix} Π_{24}^{(1)} \end{matrix}$ =-h_τn₂YD_v

$\begin{matrix} Π_{25}^{(1)} \end{matrix}$ =h_τn₁ $\begin{matrix} {\overset{̅}{C}}^{T} \end{matrix}$ Y^T

$\begin{matrix} Π_{33}^{(1)} \end{matrix}$ =h_τn₁ $\begin{matrix} {\overset{̅}{E}}^{T}_{d} \end{matrix}$ P $\begin{matrix} {\overset{̅}{E}}_{d} \end{matrix}$ - $\begin{matrix} γ_{1}^{2} \end{matrix}$ I

$\begin{matrix} Π_{34}^{(1)} \end{matrix}$ =h_τn₁ $\begin{matrix} {\overset{̅}{E}}^{T}_{d} \end{matrix}$ YD_v

$\begin{matrix} Π_{45}^{(1)} \end{matrix}$ =-h_τn₁ $\begin{matrix} {D^{T}}_{v} \end{matrix}$ Y^T

$\begin{matrix} Π_{11}^{(2)} \end{matrix}$ =P $\begin{matrix} \overset{̅}{A} \end{matrix}$ + $\begin{matrix} {\overset{̅}{A}}^{T} \end{matrix}$ P-n₂P+I+N₁+ $\begin{matrix} {N^{T}}_{1} \end{matrix}$ -h_τZ₁

$\begin{matrix} Π_{12}^{(2)} \end{matrix}$ =-Y $\begin{matrix} \overset{̅}{C} \end{matrix}$ +n₂P-N₁+ $\begin{matrix} {N^{T}}_{2} \end{matrix}$ +h_τZ₂

$\begin{matrix} Π_{22}^{(2)} \end{matrix}$ =-h_τn₃P-n₂P-N₂- $\begin{matrix} {N^{T}}_{2} \end{matrix}$ -h_τZ₃

证明先定义具有如下形式的Lyapunov函数:

V(t)= $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (t)P $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t)+(h_τ-τ ₁(t))τ ₁(t) $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (t-τ ₁(t))Q $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t-τ ₁(t))+(h_τ-τ ₁(t)) $\begin{matrix} \int_{i_{k}}^{t} \end{matrix} \begin{matrix} {\overset{\cdot}{\overset{̅}{e}}}^{T} \end{matrix}$ (s)

$\begin{matrix} \overset{\cdot}{R \overset{̅}{e}} \end{matrix}$ (s)ds+(h_τ-τ ₁(t))ϑ ^T(t)ϑ (t)(19)

式中:P=P^T> 0; Q=Q^T> 0; R=R^T> 0; S=S^T> 0, ϑ (t)= $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t)- $\begin{matrix} \overset{̅}{e} \end{matrix}$ (r_k)。

沿式(16)对Lyapunov函数求导, 可得:

$\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (t)=2 $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (t)P $\begin{matrix} \overset{\cdot}{\overset{̅}{e}} \end{matrix}$ (t)-h_τ $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (t-τ ₁(t))Q $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t-τ ₁(t))+2(h_τ-τ ₁(t)) $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (t-τ ₁(t))Q $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t-τ ₁(t))+2(h_τ-τ ₁(t))ϑ ^T(t) $\begin{matrix} \overset{\cdot}{S \overset{̅}{e}} \end{matrix}$ (t)+(h_τ-τ ₁(t)) $\begin{matrix} {\overset{\cdot}{\overset{̅}{e}}}^{T} \end{matrix}$ (t) $\begin{matrix} \overset{\cdot}{R \overset{̅}{e}} \end{matrix}$ (t)-ϑ ^T(t)Sϑ (t)- $\begin{matrix} \int_{i_{k}}^{t} \end{matrix} \begin{matrix} {\overset{\cdot}{\overset{̅}{e}}}^{T} \end{matrix}$ (s) $\begin{matrix} \overset{\cdot}{R \overset{̅}{e}} \end{matrix}$ (s)ds (20)

此时, 考虑使误差系统(16)具有渐进稳定性, 令 $\begin{matrix} \overset{̅}{d} \end{matrix}$ (t)=0, v(i_k)=0。

为了处理积分项- $\begin{matrix} \int_{i_{k}}^{t} \end{matrix} \begin{matrix} {\overset{\cdot}{\overset{̅}{e}}}^{T} \end{matrix}$ (s) $\begin{matrix} \overset{\cdot}{R \overset{̅}{e}} \end{matrix}$ (s)ds, 定义ξ (t)= $\begin{matrix} [{\overset{̅}{e}}^{T} (t), {\overset{̅}{e}}^{T} (i_{k} {)]}^{T} \end{matrix}$ , 由ϑ (t)= $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t)- $\begin{matrix} \overset{̅}{e} \end{matrix}$ (i_k), 基于柯西不等式、Jessen不等式和Schur补性质, 对于任意的矩阵N∈ $\begin{matrix} R^{2 (n + n_{f}) \times (n + n_{f})} \end{matrix}$ , 可得

- $\begin{matrix} \int_{i_{k}}^{t} \end{matrix} \begin{matrix} {\overset{\cdot}{\overset{̅}{e}}}^{T} \end{matrix}$ (s) $\begin{matrix} \overset{\cdot}{R \overset{̅}{e}} \end{matrix}$ (s)ds≤ 2ξ ^T(t)Nϑ (t)+

τ ₁(t)ξ ^T(t)Zξ (t)(21)

式中:R、N、Z满足式(18)。

将式(21)代入式(20), 可得:

$\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (t)≤ 2 $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (t) $\begin{matrix} \overset{\cdot}{P \overset{̅}{e}} \end{matrix}$ (t)-h_τ $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (t-τ ₁(t))Q $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t-τ ₁(t))+2(h_τ-τ ₁(t)) $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (t-τ ₁(t))Q $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t-τ ₁(t))+2(h_τ-τ ₁(t))ϑ ^T(t) $\begin{matrix} \overset{\cdot}{S \overset{̅}{e}} \end{matrix}$ (t)+(h_τ-τ ₁(t)) $\begin{matrix} {\overset{\cdot}{\overset{̅}{e}}}^{T} \end{matrix}$ (t) $\begin{matrix} \overset{\cdot}{R \overset{̅}{e}} \end{matrix}$ (t)-ϑ ^T(t)Sϑ (t)+2ξ ^T(t)Nϑ (t)+τ ₁(t)ξ ^T(t)Zξ (t)=

ξ ^T(t)[Γ ₁+(h_τ-τ ₁(t))Γ ₂+τ ₁(t)Z]ξ (t) (22)

式中: $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t)=M₁ξ (t); ϑ (t)=M₂ξ (t); $\begin{matrix} \overset{\cdot}{\overset{̅}{e}} \end{matrix}$ (t)=M₃ξ (t); $\begin{matrix} \overset{̅}{e} \end{matrix}$ (r_k)=M₄ξ (t); M₁=[I 0]; M₂=[I -I]; M₃=[ $\begin{matrix} \overset{̅}{A} \end{matrix}$ - $\begin{matrix} \overset{̅}{L} \end{matrix} \begin{matrix} \overset{̅}{C} \end{matrix}$ ]; M₄=[0 I]; Γ ₁=2 $\begin{matrix} {M^{T}}_{1} \end{matrix}$ PM₃-h_τ $\begin{matrix} {M^{T}}_{4} \end{matrix}$ QM₄- $\begin{matrix} {M^{T}}_{2} \end{matrix}$ SM₂+2NM₂; Γ ₂=2 $\begin{matrix} {M^{T}}_{4} \end{matrix}$ QM₄+2 $\begin{matrix} {M^{T}}_{2} \end{matrix}$ SM₃+ $\begin{matrix} {M^{T}}_{3} \end{matrix}$ RM₃。

根据文献[16]中的引理3, $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (t)< 0等价于

Γ ₁+h_τΓ ₂< 0, Γ ₁+h_τZ< 0 (23)

在零初始条件下, 当 $\begin{matrix} \overset{̅}{d} \end{matrix}$ (t)≠ 0, v(i_k)≠ 0时, 考虑如下H_∞性能指标函数:

J= $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (t)+ $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (t) $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t)- $\begin{matrix} γ_{1}^{2} \end{matrix}$ ( $\begin{matrix} {\overset{̅}{d}}^{T} \end{matrix}$ (t) $\begin{matrix} \overset{̅}{d} \end{matrix}$ (t)+

v^T(i_k)v(i_k))< 0 (24)

将式(22)中的 $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (t)代入式(24), 可得:

$\begin{matrix} Γ_{1}^{'} \end{matrix}$ +(h_τ-τ ₁(t)) $\begin{matrix} Γ_{2}^{'} \end{matrix}$ +τ ₁(t) $\begin{matrix} [\begin{matrix} Z & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}] \end{matrix}$ < 0 (25)

式中, ζ ^T(t)=[ $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (t) $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (r_k) $\begin{matrix} {\overset{̅}{d}}^{T} \end{matrix}$ (t) v^T(t_k)]; ξ (t)= $\begin{matrix} M_{4}^{'} \end{matrix}$ ζ (t), [ $\begin{matrix} {\overset{̅}{d}}^{T} \end{matrix}$ (t) v^T(t_k)]= $\begin{matrix} M_{5}^{'} \end{matrix}$ ζ (t), $\begin{matrix} \overset{̅}{e} \end{matrix}$ (i_k)=M'₆ζ (t), $\begin{matrix} M_{1}^{'} \end{matrix}$ =[I 0 0 0], $\begin{matrix} M_{2}^{'} \end{matrix}$ =[I -I 0 0], $\begin{matrix} M_{3}^{'} \end{matrix}$ =[ $\begin{matrix} \overset{̅}{A} \end{matrix}$ - $\begin{matrix} \overset{̅}{L} \end{matrix} \begin{matrix} \overset{̅}{C} \end{matrix}$ $\begin{matrix} {\overset{̅}{e}}_{d} \end{matrix} \begin{matrix} \overset{̅}{L} \end{matrix}$ D_v], $\begin{matrix} M_{4}^{'} \end{matrix}$ =[I I 0 0], $\begin{matrix} M_{5}^{'} \end{matrix}$ =[0 0 I I], $\begin{matrix} M_{6}^{'} \end{matrix}$ =[0 I 0 0], $\begin{matrix} Γ_{1}^{'} \end{matrix}$ =2 $\begin{matrix} M_{1}^{'T} \end{matrix}$ P $\begin{matrix} M_{3}^{'} \end{matrix}$ -h_τ $\begin{matrix} M_{6}^{'T} \end{matrix}$ QM₆- $\begin{matrix} M_{2}^{'T} \end{matrix}$ S $\begin{matrix} M_{2}^{'} \end{matrix}$ +2[N^T 0 0]^TM₂, $\begin{matrix} Γ_{2}^{'} \end{matrix}$ =2 $\begin{matrix} M^{'} {^{T}}_{6} \end{matrix}$ Q $\begin{matrix} M_{6}^{'} \end{matrix}$ +2 $\begin{matrix} M^{'} {^{T}}_{2} \end{matrix}$ S $\begin{matrix} M_{3}^{'} \end{matrix}$ + $\begin{matrix} M_{3}^{'T} \end{matrix}$ R $\begin{matrix} M_{3}^{'} \end{matrix}$ 。

同理, 再次使用文献[16]的引理3, 式 (25)等价于:

$\begin{matrix} \{\begin{matrix} Γ'_{1} + h_{τ} Γ'_{2} < 0 \\ Γ'_{1} + h_{τ} [\begin{matrix} Z & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}] < 0 \end{matrix} \end{matrix}$ (26)

进一步为了使式(26)中的非线性矩阵不等式转换成相应的线性矩阵不等式, 假设R=n₁P, S=n₂P, Q=n₃P, P $\begin{matrix} \overset{̅}{L} \end{matrix}$ =Y( $\begin{matrix} \overset{̅}{L} \end{matrix}$ =P^-¹Y), 并将其代入式(26)可得

$\begin{matrix} \{\begin{matrix} Γ_{1}^{″} + h_{τ} Γ_{2}^{″} < 0 \\ Γ_{1}^{″} + h_{τ} [\begin{matrix} Z & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}] < 0 \end{matrix} \end{matrix}$ (27)

限于篇幅, 此处省略 $\begin{matrix} Γ_{1}^{″} \end{matrix}$ 、 $\begin{matrix} Γ_{2}^{″} \end{matrix}$ 的相关表达式。

通过应用Schur补引理, 式(27)则等价于定理1中的式(17), 若式(17)成立, 状态估计误差e_x和故障估计误差e_f均是渐近收敛的。

从0到∞ , 对式(24)进行积分, 可得:

V(+∞ )-V(0)≤ - $\begin{matrix} \int_{0}^{+} \end{matrix}$ ( $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (s) $\begin{matrix} \overset{̅}{e} \end{matrix}$ (s))ds+ $\begin{matrix} γ_{1}^{2} \end{matrix} \begin{matrix} \int_{0}^{+} \end{matrix}$ (d^T(s)d(s))ds+ $\begin{matrix} γ_{1}^{2} \end{matrix} \begin{matrix} \overset{+ \infty}{\sum_{k = 0}} \end{matrix}$ (I_k+₁-I_k)(v^T(I_k)v(I_k)) (28)

式中:d(t)∈ L₂[0, +∞ ), v(I_k)∈ L₂[0, +∞ )。在零初始条件下V(0)=0, V(+∞ )≥ 0, 式(28)等价于 $\begin{matrix} \int_{0}^{+} \end{matrix} \begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (s) $\begin{matrix} \overset{̅}{e} \end{matrix}$ (s)ds≤ $\begin{matrix} γ_{1}^{2} \end{matrix} \begin{matrix} \int_{0}^{+} \end{matrix}$ (d^T(s)d(s))ds+ $\begin{matrix} γ_{1}^{2} \end{matrix} \begin{matrix} \overset{+ \infty}{\sum_{k = 0}} \end{matrix}$ (i_k+₁-i_k)(v^T(i_k)v(i_k)), 即 $\begin{matrix} = {\overset{̅}{e}}^{T} (t) =_{2}^{2} \end{matrix}$ ≤ $\begin{matrix} γ_{1}^{2} \end{matrix} \begin{matrix} (= {\overset{̅}{d}}^{T} (t) =_{2}^{2} + \overset{+ \infty}{\sum_{k = 0}} (i_{k + 1} - i_{k}) = v (i_{k}) =_{2}^{2}) \end{matrix}$ , 相关的H_∞性能指标成立。证毕。

注5:定理1在文献[12]的Lyapunov函数的基础上增加了一项(h_τ-τ ₁(t))τ ₁(t) $\begin{matrix} {\overset{̅}{e}}^{T} \end{matrix}$ (t-τ ₁(t))Q $\begin{matrix} \overset{̅}{e} \end{matrix}$ (t-τ ₁(t)), 可减少结果的保守性。相对于文献[12]的估计效果, 由定理1估计的连续时变故障与状态, 将具有更小的估计误差。

3 非均匀传输NCS故障调节与通信间的满意协同设计

由定理1可知, 由观测器估计及事件发生器筛选得出的状态估计误差e_x(t_k)和故障估计误差e_f(t_k)虽是渐近收敛的且满足H_∞性能指标, 但存在动态误差与静态误差, 它们势必会对容错效果造成影响, 因此在设计容错控制器时可将e_x(t_k)和e_f(t_k)视为一种外界扰动, 进而借助H_∞的理念使设计出的主动容错控制器对此类扰动均具有鲁棒性。当然, 对于τ ₂(t)E_f $\begin{matrix} \overset{\cdot}{f} \end{matrix}$ (t)同样也可将其看作是另一种外界扰动。根据定理1中得到的关于状态估计和连续时变故障估计的结果, 通过采用状态反馈和故障补偿非均匀传输容错控制器(11)可给出故障调节与通信协同设计的相关定理。

故障调节与通信满意协同设计的目标:在DETCS下, 考虑非均匀传输和执行器饱和约束的影响, 协同寻求状态反馈增益矩阵K、故障调节矩阵B⁺及事件触发权矩阵Φ , 使闭环故障NCS具有α -稳定性, 满足H_∞/H₂-性能指标且尽可能少的占有网络通信资源。

定理2 针对DETCS下的由采样数据NCS(1)衍生出的非均匀传输NCS(12), 对于给定的 $\begin{matrix} \overset{̅}{h} \end{matrix}$ 、Υ _i、 $\begin{matrix} Υ_{i}^{-} \end{matrix}$ 、α 、 $\begin{matrix} {\dot{γ}}_{1} \end{matrix}$ 、 $\begin{matrix} {\dot{γ}}_{2} \end{matrix}$ , 如果存在正定矩阵 $\begin{matrix} \dot{P} \end{matrix}$ > 0、 $\begin{matrix} \dot{S} \end{matrix}$ > 0、 $\begin{matrix} \dot{Q} \end{matrix}$ > 0、 $\begin{matrix} \dot{R} \end{matrix}$ > 0, 具有适当位数的矩阵 $\begin{matrix} \dot{N} \end{matrix}$ '、 $\begin{matrix} \dot{Z} \end{matrix}$ '、Q₁、Q₂、Q₃、Q₄、Q₅、Q₆, 且满足如下一组线性矩阵不等式:

$\begin{matrix} \{\begin{matrix} [\begin{matrix} {\dot{Π}}^{(1)} & 0 & 0 & {\dot{Ψ}}^{(1)} \\ * & - Φ & 0 & 0 \\ * & * & - δΦ & 0 \\ * & * & * & - \frac{{\overset{̅}{h}}^{2}}{4} m_{3} \dot{P} - \overset{̅}{h} n_{2} \dot{P} \end{matrix}] < 0 \\ [\begin{matrix} {\dot{Π}}^{(1)} & 0 & 0 & {\dot{Ψ}}^{(1)} \\ * & - Φ & 0 & 0 \\ * & * & - δΦ & 0 \\ * & * & * & - \frac{{\overset{̅}{h}}^{2}}{4} m_{3} \dot{P} \end{matrix}] < 0 \end{matrix} \end{matrix}$ (29)

$\begin{matrix} \{\begin{matrix} [\begin{matrix} \dot{P} & {\dot{C}}^{T} \\ * & \dot{Z}' \end{matrix}] > 0, [\begin{matrix} Q_{1} & {E^{T}}_{f} \dot{P} \\ * & Q_{2} \end{matrix}] > 0 \\ [\begin{matrix} Q_{3} & {E^{T}}_{f} \dot{S} \\ * & Q_{4} \end{matrix}] > 0, [\begin{matrix} Q_{5} & {E^{T}}_{f} \dot{R} \\ * & Q_{6} \end{matrix}] > 0 \end{matrix} \end{matrix}$ (30)

$\begin{matrix} [\begin{matrix} \dot{P} & C^{T} \\ * & {\dot{γ}}_{2}^{2} I \end{matrix}] \end{matrix}$ ≥ 0(31)

$\begin{matrix} [\begin{matrix} 1 & {\overset{̅}{f}}_{\dot{l}} \\ * & {\dot{P}}^{- 1} \end{matrix}] \end{matrix}$ > 0, 对于 $\begin{matrix} \tilde{l} \end{matrix}$ ∈ [1, m](32)

则非均匀传输主动容错控制器(11)可以确保具有连续时变故障的系统(12)在吸引域ε (P)内具有α -稳定性, 且满足如下H_∞和H₂性能指标: $\begin{matrix} = η (t) =_{2}^{2} \end{matrix}$ ≤ $\begin{matrix} {\tilde{γ}}_{1}^{2} \end{matrix} \begin{matrix} = d_{α} (t) =_{2}^{2} \end{matrix}$ + $\begin{matrix} {\tilde{γ}}_{1}^{2} \end{matrix} \begin{matrix} \overset{\infty}{\sum_{k = 0}} \end{matrix}$ (t_k+₁-t_k)( $\begin{matrix} = e_{η} (t_{k}) =_{2}^{2} \end{matrix}$ + $\begin{matrix} = e_{f_{α}} (t_{k}) =_{2}^{2} \end{matrix}$ ), $\begin{matrix} = y_{α} (t) =_{_{\infty}} \end{matrix}$ ≤ $\begin{matrix} {\tilde{γ}}_{2}^{} \end{matrix} \begin{matrix} = d_{α} (t) =_{2} \end{matrix}$ + $\begin{matrix} {\tilde{γ}}_{2}^{} \end{matrix} \begin{matrix} \overset{\infty}{\sum_{k = 0}} \end{matrix}$ (t_k+₁-, t_k)( $\begin{matrix} = e_{η} (t_{k}) =_{2} \end{matrix}$ + $\begin{matrix} = e_{f_{α}} (t_{k}) =_{2} \end{matrix}$ + $\begin{matrix} = v (t_{k}) =_{2} \end{matrix}$ ), 进一步可以得到满意容错控制器K=( $\begin{matrix} \tilde{\dot{P} B} \end{matrix}$ )^-¹ $\begin{matrix} \bar{K} \end{matrix}$ 和事件触发权矩阵Φ , 其中:

$\begin{matrix} {\dot{Π}}_{11}^{(1)} \end{matrix}$ =Λ ₁+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂(A+α I)^T $\begin{matrix} \dot{P} \end{matrix}$ (A+α I)+ $\begin{matrix} \bar{h} \end{matrix}$ n₁ $\begin{matrix} \dot{P} \end{matrix}$ (A+α I)+ $\begin{matrix} \bar{h} \end{matrix}$ n₁(A+α I)^T $\begin{matrix} \dot{P} \end{matrix}$ ;

$\begin{matrix} {\dot{Π}}_{12}^{(1)} \end{matrix}$ =Λ ₂- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₁(A+α I)^T $\begin{matrix} \dot{P} \end{matrix}$ - $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(α τ ₂(t))(A+α I)^T{Υ _i $\begin{matrix} \overset{̅}{K} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} \overset{̅}{F} \end{matrix}$ }- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(α τ ₂(t)){Υ _i $\begin{matrix} \overset{̅}{K} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} \overset{̅}{F} \end{matrix}$ };

$\begin{matrix} {\dot{Π}}_{13}^{(1)} \end{matrix}$ =Λ ₃- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(α τ ₂(t))(A+α I)^T{Υ _i $\begin{matrix} \overset{̅}{K} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} \overset{̅}{F} \end{matrix}$ }- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₁exp(α τ ₂(t)){Υ _i $\begin{matrix} \overset{̅}{K} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} \overset{̅}{F} \end{matrix}$ };

$\begin{matrix} {\dot{Π}}_{14}^{(1)} \end{matrix}$ =Λ ₄- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(α τ ₂(t))(A+α I)^T $\begin{matrix} \dot{P} \end{matrix}$ E_f- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₁exp(α τ ₂(t)) $\begin{matrix} \dot{P} \end{matrix}$ E_f;

$\begin{matrix} {\dot{Π}}_{15}^{(1)} \end{matrix}$ =Λ ₅+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂(A+α I)^T $\begin{matrix} \dot{P} \end{matrix}$ E_d+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₁ $\begin{matrix} \dot{P} \end{matrix}$ E_d;

$\begin{matrix} {\dot{Π}}_{22}^{(1)} \end{matrix}$ =Λ ₆+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₃ $\begin{matrix} \dot{P} \end{matrix}$ + $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₁exp(α τ ₂(t)){Υ _i $\begin{matrix} \overset{̅}{K} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} \overset{̅}{F} \end{matrix}$ }+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₁exp(α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ };

$\begin{matrix} {\dot{Π}}_{23}^{(1)} \end{matrix}$ = $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₁exp(α τ ₂(t)){Υ _i $\begin{matrix} \overset{̅}{K} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} \overset{̅}{F} \end{matrix}$ };

$\begin{matrix} {\dot{Π}}_{24}^{(1)} \end{matrix}$ =Λ ₇+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(2α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ }E_f+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₁exp(α τ ₂(t)) $\begin{matrix} \dot{P} \end{matrix}$ E_f;

$\begin{matrix} {\dot{Π}}_{25}^{(1)} \end{matrix}$ =Λ ₈- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ }E_d- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₁ $\begin{matrix} \dot{P} \end{matrix}$ E_d;

$\begin{matrix} {\dot{Π}}_{34}^{(1)} \end{matrix}$ =Λ ₁₀+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(2α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ }E_f;

$\begin{matrix} {\dot{Π}}_{35}^{(1)} \end{matrix}$ =Λ ₁₁- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ }E_d;

$\begin{matrix} {\dot{Π}}_{44}^{(1)} \end{matrix}$ =Λ ₁₃- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(2α τ ₂(t)) $\begin{matrix} {E^{T}}_{f} \end{matrix} \begin{matrix} \dot{P} \end{matrix}$ E_f;

$\begin{matrix} {\dot{Π}}_{45}^{(1)} \end{matrix}$ =Λ ₁₄- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(α τ ₂(t)) $\begin{matrix} {E^{T}}_{f} \end{matrix} \begin{matrix} \dot{P} \end{matrix}$ E_d;

$\begin{matrix} {\dot{Π}}_{55}^{(1)} \end{matrix}$ =Λ ₁₅+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂ $\begin{matrix} {E^{T}}_{d} \end{matrix} \begin{matrix} \dot{P} \end{matrix}$ E_d;

$\begin{matrix} {\dot{Ψ}}_{21}^{(1)} \end{matrix}$ =Λ ₉+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ };

$\begin{matrix} Ψ_{31}^{(1)} \end{matrix}$ =Λ ₁₂+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₂exp(α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ };

$\begin{matrix} {\dot{Π}}_{11}^{(1)} \end{matrix}$ =Λ ₁+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ Z₁+ $\begin{matrix} \overset{̅}{h} \end{matrix}$ m₁ $\begin{matrix} \dot{P} \end{matrix}$ ;

$\begin{matrix} {\dot{Π}}_{12}^{(1)} \end{matrix}$ =Λ ₂-hZ₂;

$\begin{matrix} {\dot{Π}}_{13}^{(1)} \end{matrix}$ =Λ ₃;

$\begin{matrix} {\dot{Π}}_{14}^{(1)} \end{matrix}$ =Λ ₄;

$\begin{matrix} {\dot{Π}}_{15}^{(1)} \end{matrix}$ =Λ ₅;

$\begin{matrix} {\dot{Π}}_{22}^{(1)} \end{matrix}$ =Λ ₆- $\begin{matrix} \overset{̅}{h} \end{matrix}$ n₃ $\begin{matrix} \dot{P} \end{matrix}$ + $\begin{matrix} \overset{̅}{h} \end{matrix}$ Z₃;

$\begin{matrix} {\dot{Π}}_{24}^{(1)} \end{matrix}$ =Λ ₇;

$\begin{matrix} {\dot{Π}}_{25}^{(1)} \end{matrix}$ =Λ ₈;

$\begin{matrix} {\dot{Π}}_{33}^{(1)} \end{matrix}$ =- $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix}$ I;

$\begin{matrix} {\dot{Π}}_{34}^{(1)} \end{matrix}$ =Λ ₁₀;

$\begin{matrix} {\dot{Π}}_{35}^{(1)} \end{matrix}$ =Λ ₁₁;

$\begin{matrix} {\dot{Π}}_{44}^{(1)} \end{matrix}$ =-Λ ₁₃;

$\begin{matrix} {\dot{Π}}_{45}^{(1)} \end{matrix}$ =Λ ₁₄;

$\begin{matrix} {\dot{Π}}_{55}^{(1)} \end{matrix}$ =Λ ₁₅;

$\begin{matrix} {\dot{Ψ}}_{21}^{(1)} \end{matrix}$ =Λ ₉;

$\begin{matrix} {\dot{Ψ}}_{31}^{(1)} \end{matrix}$ =Λ ₁₂;

Λ ₁= $\begin{matrix} \dot{P} \end{matrix}$ (A+α I)+(A+α I)^T $\begin{matrix} \dot{P} \end{matrix}$ +N₁+ $\begin{matrix} {N^{T}}_{1} \end{matrix}$ +I+ $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃(A+α I)^T $\begin{matrix} \dot{P} \end{matrix}$ (A+α I)+ $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₂ $\begin{matrix} \dot{P} \end{matrix}$ -n₁ $\begin{matrix} \dot{P} \end{matrix}$ ;

Λ ₂=-exp(α τ ₂(t)){Υ _i $\begin{matrix} \overset{̅}{K} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} \overset{̅}{F} \end{matrix}$ }- $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃× exp(α τ ₂(t))(A+α I)^T{Υ _i $\begin{matrix} \overset{̅}{K} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} \overset{̅}{F} \end{matrix}$ }- $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₂ $\begin{matrix} \dot{P} \end{matrix}$ +n₁ $\begin{matrix} \dot{P} \end{matrix}$ -N₁+ $\begin{matrix} {N^{T}}_{2} \end{matrix}$ ;

Λ ₃=-exp(α τ ₂(t)){Υ _i $\begin{matrix} \overset{̅}{K} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} \overset{̅}{F} \end{matrix}$ }- $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃× exp(α τ ₂(t))(A+α I)^T{Υ _i $\begin{matrix} \overset{̅}{K} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} \overset{̅}{F} \end{matrix}$ };

Λ ₄=-exp(α τ ₂(t)) $\begin{matrix} \dot{P} \end{matrix}$ E_f- $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃exp(α τ ₂(t))×

(A+α I)^T $\begin{matrix} \dot{P} \end{matrix}$ E_f;

Λ ₅= $\begin{matrix} \dot{P} \end{matrix}$ E_d+ $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃(A+α I)^T $\begin{matrix} \dot{P} \end{matrix}$ E_d;

Λ ₆=-n₁ $\begin{matrix} \dot{P} \end{matrix}$ -N₂- $\begin{matrix} {N^{T}}_{2} \end{matrix}$ + $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₂ $\begin{matrix} \dot{P} \end{matrix}$ ;

Λ ₇= $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃exp(2α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ }E_f;

Λ ₈=- $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃exp(α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ }E_d;

Λ ₉= $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃exp(α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ };

Λ ₁₀= $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃exp(2α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ }E_f;

Λ ₁₁=- $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃exp(α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ }E_d;

Λ ₁₂= $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃exp(α τ ₂(t)){Υ _i $\begin{matrix} {\overset{̅}{K}}^{T} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} {\overset{̅}{F}}^{T} \end{matrix}$ };

Λ ₁₃=- $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix}$ I- $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃exp(2α τ ₂(t)) $\begin{matrix} {E^{T}}_{f} \end{matrix} \begin{matrix} \dot{P} \end{matrix}$ E_f;

Λ ₁₄=- $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃exp(α τ ₂(t)) $\begin{matrix} {E^{T}}_{f} \end{matrix} \begin{matrix} \dot{P} \end{matrix}$ E_d;

Λ ₁₅=- $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix}$ I+ $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix}$ m₃ $\begin{matrix} {E^{T}}_{d} \end{matrix} \begin{matrix} \dot{P} \end{matrix}$ E_d。

证明:为了确保闭环调节系统具有α -稳定性, 需要在证明过程中引入如下变换:

η (t)=exp(α t)x(t),

η (t-τ ₂(t))=exp(α (t-τ ₂(t)))x(t-τ ₂(t)),

e_η(t-τ ₂(t))=exp(α (t-τ ₂(t)))e_x(t-τ ₂(t)),

$\begin{matrix} e_{f_{α}} \end{matrix}$ (t-τ ₂(t))=exp(α (t-τ ₂(t)))e_f(t-τ ₂(t)),

$\begin{matrix} {\overset{\cdot}{f}}_{α} \end{matrix}$ (t)=exp(α t) $\begin{matrix} \overset{\cdot}{f} \end{matrix}$ (t),

d_α(t)=exp(α t)d(t),

v_α(t_k)=exp(α t_k)v(t_k)。

则式(12)等价于:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{η} (t) = \dot{A} η (t) - sat (\dot{B} \dot{K} η (t - τ_{2} (t))) - sat (\dot{B} \dot{K} e_{η} (t \\ - τ_{2} (t))) - {\overset{̅}{e}}_{f} e_{f_{α}} (t - τ_{2} (t)) + τ_{2} (t) E_{f} {\overset{\cdot}{f}}_{α} (t) \\ + E_{d} d_{α} (t) \\ y_{α} (t) = Cη (t - τ_{2} (t)) \end{matrix} \end{matrix}$ (33)

式中: $\begin{matrix} \dot{A} \end{matrix}$ =A+α I; $\begin{matrix} \dot{B} \end{matrix} \begin{matrix} \dot{K} \end{matrix}$ =exp(α τ ₂(t))BK; $\begin{matrix} {\overset{̅}{E}}_{f} \end{matrix}$ =exp(α τ ₂(t))E_f。

当t∈ [t_k+ $\begin{matrix} τ_{t_{k}} \end{matrix}$ , t_k+₁+ $\begin{matrix} τ_{t_{k + 1}} \end{matrix}$ )时, 选取如下一组Lyapunov函数:

V(η (t))=η ^T(t) $\begin{matrix} \dot{P} \end{matrix}$ η (t)+( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t))τ ₂(t)× η ^T(t-τ ₂(t)) $\begin{matrix} \tilde{Q} \end{matrix}$ η (t-τ ₂(t))+( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t))×

$\begin{matrix} \int_{t_{k}}^{t} \end{matrix} \begin{matrix} {\overset{\cdot}{η}}^{T} \end{matrix}$ (s) $\begin{matrix} \dot{R} \end{matrix} \begin{matrix} \overset{\cdot}{η} \end{matrix}$ (s)ds+( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t)) $\begin{matrix} {\bar{η}}^{T} \end{matrix}$ (t) $\begin{matrix} \dot{S} \end{matrix} \begin{matrix} \bar{η} \end{matrix}$ (t) (34)

式中: $\begin{matrix} \dot{P} \end{matrix}$ = $\begin{matrix} {\dot{P}}^{T} \end{matrix}$ > 0, $\begin{matrix} \dot{Q} \end{matrix}$ = $\begin{matrix} {\dot{Q}}^{T} \end{matrix}$ > 0, $\begin{matrix} \dot{R} \end{matrix}$ = $\begin{matrix} {\dot{R}}^{T} \end{matrix}$ > 0, $\begin{matrix} \dot{S} \end{matrix}$ = $\begin{matrix} {\dot{S}}^{T} \end{matrix}$ > 0, $\begin{matrix} \overset{̅}{η} \end{matrix}$ (t)=η (t)-η (t_k)。

首先, 证明系统具有稳定性, 设e_η(t-τ ₂(t))=0, $\begin{matrix} e_{f_{α}} \end{matrix}$ (t-τ ₂(t))=0, d_α(t)=0, v_α(t_k)=0。

按照式(33)的轨迹, 对V(η (t))进行求导, 可得:

$\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (η (t))=2η ^T(t) $\begin{matrix} \dot{P} \end{matrix} \begin{matrix} \overset{\cdot}{η} \end{matrix}$ (t)- $\begin{matrix} \overset{̅}{h} \end{matrix}$ η ^T(t-τ ₂(t)) $\begin{matrix} \dot{Q} \end{matrix}$ η (t-τ ₂(t))+2( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t))η ^T(t-τ ₂(t)) $\begin{matrix} \dot{Q} \end{matrix}$ η (t-τ ₂(t))- $\begin{matrix} \int_{t_{k}}^{t} \end{matrix} \begin{matrix} {\overset{\cdot}{η}}^{T} \end{matrix}$ (s) $\begin{matrix} \dot{R} \end{matrix} \begin{matrix} \overset{\cdot}{η} \end{matrix}$ (s)ds+( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t)) $\begin{matrix} \overset{̅}{η} \end{matrix}$ T(t) $\begin{matrix} \dot{R} \end{matrix} \begin{matrix} \overset{\cdot}{η} \end{matrix}$ (t)- $\begin{matrix} {\overset{̅}{η}}^{T} \end{matrix}$ (t) $\begin{matrix} \dot{S} \end{matrix} \begin{matrix} \bar{η} \end{matrix}$ (t)+2( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t)) $\begin{matrix} {\overset{̅}{η}}^{T} \end{matrix}$ (t) $\begin{matrix} \dot{S} \end{matrix} \begin{matrix} \overset{\cdot}{η} \end{matrix}$ (t) (35)

对执行器饱和约束, 应用文献[11]中的引理1可得如下定义:η (t)= $\begin{matrix} {\dot{M}}_{1} \end{matrix} \begin{matrix} \dot{ξ} \end{matrix}$ (t); $\begin{matrix} \overset{̅}{η} \end{matrix}$ (t)= $\begin{matrix} {\dot{M}}_{2} \end{matrix} \begin{matrix} \dot{ξ} \end{matrix}$ (t); $\begin{matrix} \overset{\cdot}{η} \end{matrix}$ (t)= $\begin{matrix} {\dot{M}}_{3} \end{matrix} \begin{matrix} \dot{ξ} \end{matrix}$ (t)+τ ₂(t)E_f $\begin{matrix} {\overset{\cdot}{f}}_{α} \end{matrix}$ (t); η (t-τ ₂(t))= η (t_k)= $\begin{matrix} {\dot{M}}_{4} \end{matrix} \begin{matrix} \dot{ξ} \end{matrix}$ (t), 其中, $\begin{matrix} \dot{ξ} \end{matrix}$ (t)=[η ^T(t), η ^T(t_k)] $\begin{matrix} {\dot{M}}_{1} \end{matrix}$ =[I 0], $\begin{matrix} {\dot{M}}_{2} \end{matrix}$ =[I -I], $\begin{matrix} {\dot{M}}_{3} \end{matrix}$ =[ $\begin{matrix} \dot{A} \end{matrix}$ - $\begin{matrix} \dot{B} \end{matrix}$ co{Υ _i $\begin{matrix} \dot{K} \end{matrix}$ + $\begin{matrix} Υ_{i}^{-} \end{matrix} \begin{matrix} \dot{F} \end{matrix}$ }], $\begin{matrix} {\dot{M}}_{4} \end{matrix}$ =[0 I]。

可将 $\begin{matrix} \overset{̅}{η} \end{matrix}$ (t)写成:

$\begin{matrix} \overset{̅}{η} \end{matrix}$ (t)=η (t)-η (t_k)= $\begin{matrix} \int_{t_{k}}^{t} \end{matrix} \begin{matrix} \overset{\cdot}{η} \end{matrix}$ (s)ds (36)

基于Schur性质、柯西不等式以及Jensen不等式来处理 $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (t)中的积分项- $\begin{matrix} \int_{t_{k}}^{t} \end{matrix} \begin{matrix} {\overset{\cdot}{η}}^{T} \end{matrix}$ (s) $\begin{matrix} \dot{R} \end{matrix} \begin{matrix} \overset{\cdot}{η} \end{matrix}$ (s)ds, 可得:

- $\begin{matrix} \int_{t_{k}}^{t} \end{matrix} \begin{matrix} {\overset{\cdot}{η}}^{T} \end{matrix}$ (s) $\begin{matrix} \dot{R} \end{matrix} \begin{matrix} \overset{\cdot}{η} \end{matrix}$ (s)ds≤ 2 $\begin{matrix} {\dot{ξ}}^{T} \end{matrix}$ (t) $\begin{matrix} \dot{N} \end{matrix} \begin{matrix} \overset{̅}{η} \end{matrix}$ (t)+

τ ₂(t) $\begin{matrix} {\dot{ξ}}^{T} \end{matrix}$ (t) $\begin{matrix} \dot{Z} \end{matrix} \begin{matrix} \dot{ξ} \end{matrix}$ (t) (37)

式中: $\begin{matrix} \dot{R} \end{matrix}$ ∈ R^{n× n}、 $\begin{matrix} \dot{N} \end{matrix}$ ∈ R²^{n× n}、 $\begin{matrix} \dot{Z} \end{matrix}$ ∈ R²^n×²ⁿ 满足式(30)。

结合文献[11]中的引理1和式(37), 可得式(35)等价于:

$\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (t)≤ $\begin{matrix} \max_{i \in [1, 2, \dots, 2^{m}]} \end{matrix}$ { $\begin{matrix} {\dot{ξ}}^{T} \end{matrix}$ (t)[2 $\begin{matrix} {\dot{M}}^{T}_{1} \end{matrix} \begin{matrix} \dot{P} \end{matrix} \begin{matrix} {\dot{M}}_{3} \end{matrix}$ - $\begin{matrix} \overset{̅}{h} \end{matrix} \begin{matrix} {\dot{M}}^{T}_{4} \end{matrix} \begin{matrix} \dot{Q} \end{matrix} \begin{matrix} {\dot{M}}_{4} \end{matrix}$ - $\begin{matrix} {\dot{M}}^{T}_{2} \end{matrix} \begin{matrix} \dot{S} \end{matrix} \begin{matrix} {\dot{M}}_{2} \end{matrix}$ +2 $\begin{matrix} \dot{N} \end{matrix} \begin{matrix} {\dot{M}}_{2} \end{matrix}$ +( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t))(2 $\begin{matrix} {\dot{M}}^{T}_{4} \end{matrix} \begin{matrix} \dot{Q} \end{matrix} \begin{matrix} {\dot{M}}_{4} \end{matrix}$ + $\begin{matrix} {\dot{M}}^{T}_{3} \end{matrix} \begin{matrix} \dot{R} \end{matrix} \begin{matrix} {\dot{M}}_{3} \end{matrix}$ +2 $\begin{matrix} {\dot{M}}^{T}_{2} \end{matrix} \begin{matrix} \dot{S} \end{matrix} \begin{matrix} {\dot{M}}_{3} \end{matrix}$ )+τ ₂(t) $\begin{matrix} \dot{Z} \end{matrix}$ ] $\begin{matrix} \dot{ξ} \end{matrix}$ (t)+2τ ₂(t)η ^T(t) $\begin{matrix} \dot{P} \end{matrix}$ E_f $\begin{matrix} {\overset{\cdot}{f}}_{α} \end{matrix}$ (t)+2( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t))( $\begin{matrix} {\overset{̅}{η}}^{T} \end{matrix}$ (t)×

$\begin{matrix} \dot{S} \end{matrix}$ E_f $\begin{matrix} {\overset{\cdot}{f}}_{α} \end{matrix}$ (t)+ $\begin{matrix} {\dot{ξ}}^{T} \end{matrix}$ (t) $\begin{matrix} {\dot{M}}^{T}_{3} \end{matrix} \begin{matrix} \dot{R} \end{matrix}$ E_f $\begin{matrix} {\overset{\cdot}{f}}_{α} \end{matrix}$ (t))+( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t))×

$\begin{matrix} τ_{2}^{2} \end{matrix}$ (t) $\begin{matrix} {\overset{\cdot}{f}}^{T}_{α} \end{matrix}$ (t) $\begin{matrix} {E^{T}}_{f} \end{matrix} \begin{matrix} \dot{R} \end{matrix}$ E_f $\begin{matrix} {\overset{\cdot}{f}}_{α} \end{matrix}$ (t)} (38)

根据(30)和Moon不等式, 可得:

2τ ₂(t)η ^T(t) $\begin{matrix} \dot{P} \end{matrix}$ E_f $\begin{matrix} {\overset{\cdot}{f}}_{α} \end{matrix}$ (t)≤ τ ₂(t)η ^T(t)Q₂η (t)+ $\begin{matrix} \overset{̅}{h} \end{matrix} \begin{matrix} f_{0}^{2} \end{matrix}$ λ _max(Q₁) (39)

2( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t)) $\begin{matrix} {\overset{̅}{η}}^{T} \end{matrix}$ (t) $\begin{matrix} \dot{S} \end{matrix}$ E_f $\begin{matrix} {\overset{\cdot}{f}}_{α} \end{matrix}$ (t)≤ $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix} \begin{matrix} {\overset{̅}{η}}^{T} \end{matrix}$ (t)Q₄ $\begin{matrix} \overset{̅}{η} \end{matrix}$ (t)+ $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix} \begin{matrix} f_{0}^{2} \end{matrix}$ λ _max(Q₃) (40)

2( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t)) $\begin{matrix} {\dot{ξ}}^{T} \end{matrix}$ (t) $\begin{matrix} {\dot{M}}^{T}_{3} \end{matrix} \begin{matrix} \dot{R} \end{matrix}$ E_f $\begin{matrix} {\overset{\cdot}{f}}_{α} \end{matrix}$ (t)≤ $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix} \begin{matrix} {\dot{ξ}}^{T} \end{matrix}$ (t) $\begin{matrix} {\dot{M}}^{T}_{3} \end{matrix}$ Q₆ $\begin{matrix} {\dot{M}}_{3} \end{matrix} \begin{matrix} \dot{ξ} \end{matrix}$ (t)+ $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix} \begin{matrix} f_{0}^{2} \end{matrix}$ λ _max(Q₅) (41)

( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t)) $\begin{matrix} τ_{2}^{2} \end{matrix}$ (t) $\begin{matrix} {\overset{\cdot}{f}}^{T}_{α} \end{matrix}$ (t) $\begin{matrix} {E^{T}}_{f} \end{matrix} \begin{matrix} \dot{R} \end{matrix}$ E_f $\begin{matrix} {\overset{\cdot}{f}}_{α} \end{matrix}$ (t)≤ $\begin{matrix} \frac{{\overset{̅}{h}}^{3}}{8} \end{matrix} \begin{matrix} f_{0}^{2} \end{matrix}$ λ _max( $\begin{matrix} {E^{T}}_{f} \end{matrix} \begin{matrix} \dot{R} \end{matrix}$ E_f) (42)

将式(39)~(42)代入式(38)中, 可得:

式中:

$\begin{matrix} {\dot{Γ}}_{1} \end{matrix}$ =2 $\begin{matrix} {\dot{M}}^{T}_{1} \end{matrix} \begin{matrix} \dot{P} \end{matrix} \begin{matrix} {\dot{M}}_{3} \end{matrix}$ - $\begin{matrix} \overset{̅}{h} \end{matrix} \begin{matrix} {\dot{M}}^{T}_{4} \end{matrix} \begin{matrix} \dot{Q} \end{matrix} \begin{matrix} {\dot{M}}_{4} \end{matrix}$ - $\begin{matrix} {\dot{M}}^{T}_{2} \end{matrix} \begin{matrix} \dot{S} \end{matrix} \begin{matrix} {\dot{M}}_{2} \end{matrix}$ +2 $\begin{matrix} \dot{N} \end{matrix} \begin{matrix} {\dot{M}}_{2} \end{matrix}$ + $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix} \begin{matrix} {\dot{M}}^{T}_{2} \end{matrix}$ Q₄ $\begin{matrix} {\dot{M}}_{2} \end{matrix}$ + $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix} \begin{matrix} {\dot{M}}^{T}_{3} \end{matrix}$ Q₆ $\begin{matrix} {\dot{M}}_{3} \end{matrix}$ ;

$\begin{matrix} {\dot{Γ}}_{2} \end{matrix}$ =2 $\begin{matrix} {\dot{M}}^{T}_{4} \end{matrix} \begin{matrix} \dot{Q} \end{matrix} \begin{matrix} {\dot{M}}_{4} \end{matrix}$ + $\begin{matrix} {\dot{M}}^{T}_{3} \end{matrix} \begin{matrix} \dot{R} \end{matrix}$ , $\begin{matrix} {\dot{M}}_{3} \end{matrix}$ +2 $\begin{matrix} {\dot{M}}^{T}_{2} \end{matrix} \begin{matrix} \dot{S} \end{matrix} \begin{matrix} {\dot{M}}_{3} \end{matrix}$ ;

$\begin{matrix} {\dot{Γ}}_{3} \end{matrix}$ = $\begin{matrix} \dot{Z} \end{matrix}$ + $\begin{matrix} {\dot{M}}^{T}_{1} \end{matrix}$ Q₂ $\begin{matrix} {\dot{M}}_{1} \end{matrix}$ ;

δ = $\begin{matrix} \overset{̅}{h} \end{matrix} \begin{matrix} f_{0}^{2} \end{matrix}$ λ _max(Q₁)+ $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix} \begin{matrix} f_{0}^{2} \end{matrix}$ λ _max(Q₂)+ $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix} \begin{matrix} f_{0}^{2} \end{matrix}$ λ _max(Q₅)+ $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{8} \end{matrix} \begin{matrix} f_{0}^{2} \end{matrix}$ λ _max( $\begin{matrix} {E^{T}}_{f} \end{matrix} \begin{matrix} \dot{R} \end{matrix}$ E_f)。

式(43)中, 若 $\begin{matrix} {\dot{Γ}}_{1} \end{matrix}$ +( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t)) $\begin{matrix} {\dot{Γ}}_{2} \end{matrix}$ +τ ₂(t) $\begin{matrix} {\dot{Γ}}_{3} \end{matrix}$ < 0, 那么有 $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (t)≤ -ε $\begin{matrix} = \dot{ξ} (t) =^{2} \end{matrix}$ +δ , 其中, ε = λ _min[-( $\begin{matrix} {\dot{Γ}}_{1} \end{matrix}$ +( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t)) $\begin{matrix} {\dot{Γ}}_{2} \end{matrix}$ +τ ₂(t) $\begin{matrix} {\dot{Γ}}_{3} \end{matrix}$ )], 所以若ε $\begin{matrix} = \dot{ξ} (t) =^{2} \end{matrix}$ > δ 时, 则 $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (t)< 0。根据Lyapunov稳定性理论 $\begin{matrix} \dot{ξ} \end{matrix}$ (t)最终将收敛于集合Ψ = { $\begin{matrix} \dot{ξ} \end{matrix}$ (t)| $\begin{matrix} = \dot{ξ} (t) =^{2} \end{matrix}$ < $\begin{matrix} \frac{δ}{ε} \end{matrix}$ }, 可得系统(33)是一致最终有界的。

在零初始条件下, 设e_η(t-τ ₂(t))≠ 0, $\begin{matrix} e_{f_{α}} \end{matrix}$ (t-τ ₂(t))≠ 0, d_α(t)≠ 0。做如下定义, η (t)= $\begin{matrix} {\dot{M}}_{1}^{'T} \end{matrix} \begin{matrix} \dot{ζ} \end{matrix}$ (t), $\begin{matrix} \overset{̅}{η} \end{matrix}$ (t)= $\begin{matrix} {\dot{M}}_{2}^{'T} \end{matrix} \begin{matrix} \dot{ζ} \end{matrix}$ (t), $\begin{matrix} \overset{\cdot}{η} \end{matrix}$ (t)= $\begin{matrix} {\dot{M}}_{3}^{'T} \end{matrix} \begin{matrix} \dot{ζ} \end{matrix}$ (t)+τ ₂(t)E_f $\begin{matrix} {\overset{\cdot}{f}}_{α} \end{matrix}$ (t), η (t_k)= $\begin{matrix} {\dot{M}}_{4}^{'T} \end{matrix} \begin{matrix} \dot{ζ} \end{matrix}$ (t)其中, $\begin{matrix} {\dot{M}}_{1}^{'T} \end{matrix}$ =[I 0 0 0 0 0 0], $\begin{matrix} {\dot{M}}_{2}^{'T} \end{matrix}$ =[I -I 0 0 0 0 0], $\begin{matrix} {\dot{M}}_{3}^{'T} \end{matrix}$ =[ $\begin{matrix} \dot{A} \end{matrix}$ - $\begin{matrix} \dot{B} \end{matrix}$ {Υ _iK+ $\begin{matrix} Υ_{i}^{-} \end{matrix}$ F} - $\begin{matrix} \dot{B} \end{matrix}$ {Υ _iK+ $\begin{matrix} Υ_{i}^{-} \end{matrix}$ F} - $\begin{matrix} {\dot{E}}_{f} \end{matrix}$ E_d 0 0], $\begin{matrix} \dot{M} \end{matrix} \begin{matrix} {'^{T}}_{4} \end{matrix}$ =[0 I 0 0 0 0 0], $\begin{matrix} \dot{ζ} \end{matrix}$ (t)=[ $\begin{matrix} {\dot{ξ}}^{T} \end{matrix}$ (t) $\begin{matrix} {e^{T}}_{η} \end{matrix}$ (t_k) $\begin{matrix} {e^{T}}_{f_{α}} \end{matrix}$ (t_k) $\begin{matrix} {d^{T}}_{α} \end{matrix}$ (t) $\begin{matrix} {\dot{e}}^{T}_{α} \end{matrix}$ (t) $\begin{matrix} {\dot{η}}^{T} \end{matrix}$ (t_k)]。

在DETCS下, 考虑如下性能指标函数:

J₁= $\begin{matrix} \overset{\cdot}{\dot{V}} \end{matrix}$ (η (t))+η ^T(t)η (t)- $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix}$ ( $\begin{matrix} {d^{T}}_{α} \end{matrix}$ (t)d_α(t)+

$\begin{matrix} {e^{T}}_{η} \end{matrix}$ (t_k)e_η(t_k)+ $\begin{matrix} {e^{T}}_{f_{α}} \end{matrix}$ (t_k) $\begin{matrix} e_{f_{α}} \end{matrix}$ (t_k)) (44)

式中: $\begin{matrix} \overset{\cdot}{\dot{V}} \end{matrix}$ (η (t))= $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (η (t))+ $\begin{matrix} {\dot{e}}^{T}_{α} \end{matrix}$ (i_k)Φ $\begin{matrix} {\dot{e}}_{α} \end{matrix}$ (i_k) - $\begin{matrix} {\dot{e}}^{T}_{α} \end{matrix}$ (i_k)Φ $\begin{matrix} {\dot{e}}_{α} \end{matrix}$ (i_k), 基于式(43)中 $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ (η (t))的结果, 使得J₁< 0成立的充分条件是:

$\begin{matrix} {\dot{Γ}}_{1}^{'} \end{matrix}$ +( $\begin{matrix} \overset{̅}{h} \end{matrix}$ -τ ₂(t)) $\begin{matrix} {\dot{Γ}}_{2}^{'} \end{matrix}$ +τ ₂(t) $\begin{matrix} {\dot{Γ}}_{3}^{'} \end{matrix}$ < 0(45)

式中: $\begin{matrix} {\dot{Γ}}_{1}^{'} \end{matrix}$ =2 $\begin{matrix} {\dot{M}}_{1}^{'T} \end{matrix} \begin{matrix} \dot{P} \end{matrix} \begin{matrix} {\dot{M}}_{3}^{'} \end{matrix}$ - $\begin{matrix} \overset{̅}{h} \end{matrix} \begin{matrix} {\dot{M}}_{4}^{'T} \end{matrix} \begin{matrix} \dot{Q} \end{matrix} \begin{matrix} {\dot{M}}_{4}^{'} \end{matrix}$ - $\begin{matrix} {\dot{M}}_{2}^{'T} \end{matrix} \begin{matrix} \dot{S} \end{matrix} \begin{matrix} {\dot{M}}_{2}^{'} \end{matrix}$ +2 $\begin{matrix} {\dot{N}}^{'} \end{matrix} \begin{matrix} {\dot{M}}_{2}^{'} \end{matrix}$ + $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix} \begin{matrix} {\dot{M}}_{2}^{'T} \end{matrix}$ Q₄ $\begin{matrix} {\dot{M}}_{2}^{'} \end{matrix}$ + $\begin{matrix} \frac{{\overset{̅}{h}}^{2}}{4} \end{matrix} \begin{matrix} {\dot{M}}_{3}^{'T} \end{matrix}$ Q₆ $\begin{matrix} {\dot{M}}_{3}^{'} \end{matrix}$ + $\begin{matrix} {\dot{e}}^{T}_{α} \end{matrix}$ (i_k)Φ $\begin{matrix} {\dot{e}}_{α} \end{matrix}$ (i_k)- $\begin{matrix} {\dot{e}}^{T}_{α} \end{matrix}$ (i_k)Φ $\begin{matrix} {\dot{e}}_{α} \end{matrix}$ (i_k)+ $\begin{matrix} {\dot{M}}_{1}^{'T} \end{matrix} \begin{matrix} {\dot{M}}_{1}^{'} \end{matrix}$ - $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix} \begin{matrix} {d^{T}}_{α} \end{matrix}$ (t)d_α(t)- $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix} \begin{matrix} {e^{T}}_{η} \end{matrix}$ (t_k)e_η(t_k)- $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix} \begin{matrix} {e^{T}}_{f_{α}} \end{matrix}$ (t_k) $\begin{matrix} e_{f_{α}} \end{matrix}$ (t_k);

$\begin{matrix} {\dot{Γ}}_{2}^{'} \end{matrix}$ =2 $\begin{matrix} {\dot{M}}^{'} {^{T}}_{4} \end{matrix} \begin{matrix} \dot{Q} \end{matrix} \begin{matrix} {\dot{M}}_{4}^{'} \end{matrix}$ + $\begin{matrix} {\dot{M}}_{3}^{'T} \end{matrix} \begin{matrix} \dot{R} \end{matrix} \begin{matrix} {\dot{M}}_{3}^{'} \end{matrix}$ +2 $\begin{matrix} {\dot{M}}_{2}^{'T} \end{matrix} \begin{matrix} \dot{S} \end{matrix} \begin{matrix} {\dot{M}}_{3}^{'} \end{matrix}$ ,

$\begin{matrix} {\dot{Γ}}_{3}^{'} \end{matrix}$ = $\begin{matrix} {\dot{M}}_{5}^{'T} \end{matrix} \begin{matrix} \dot{Z} \end{matrix} \begin{matrix} {\dot{M}}_{5}^{'} \end{matrix}$ + $\begin{matrix} {\dot{M}}_{1}^{'T} \end{matrix}$ Q₂ $\begin{matrix} {\dot{M}}_{1}^{'} \end{matrix}$ ;

$\begin{matrix} {\dot{M}}_{5}^{'} \end{matrix}$ =[I 0 0 0 0 0]。

根据文献[16]中引理3, 式(45)成立的充分必要条件是:

$\begin{matrix} {\dot{Γ}}_{1}^{'} \end{matrix}$ + $\begin{matrix} \overset{̅}{h} \end{matrix} \begin{matrix} {\dot{Γ}}_{2}^{'} \end{matrix}$ < 0, $\begin{matrix} {\dot{Γ}}_{1}^{'} \end{matrix}$ + $\begin{matrix} \overset{̅}{h} \end{matrix} \begin{matrix} {\dot{Γ}}_{3}^{'} \end{matrix}$ < 0 (46)

进一步为了使式(46)中的非线性矩阵不等式转换成相应的线性矩阵不等式, 假设 $\begin{matrix} \dot{S} \end{matrix}$ =n₁ $\begin{matrix} \dot{P} \end{matrix}$ , $\begin{matrix} \dot{R} \end{matrix}$ =n₂ $\begin{matrix} \dot{P} \end{matrix}$ , $\begin{matrix} \dot{Q} \end{matrix}$ =n₃ $\begin{matrix} \dot{P} \end{matrix}$ , Q₂=m₁ $\begin{matrix} \dot{P} \end{matrix}$ , Q₄=m₂ $\begin{matrix} \dot{P} \end{matrix}$ , Q₆=m₃ $\begin{matrix} \dot{P} \end{matrix}$ , $\begin{matrix} \overset{̅}{K} \end{matrix}$ = $\begin{matrix} \dot{P} \end{matrix} \begin{matrix} \dot{B} \end{matrix} \begin{matrix} \dot{K} \end{matrix}$ , $\begin{matrix} \overset{̅}{F} \end{matrix}$ = $\begin{matrix} \dot{P} \end{matrix} \begin{matrix} \dot{B} \end{matrix} \begin{matrix} \dot{F} \end{matrix}$ , 式(46)等价于:

限于篇幅, 此处将省略 $\begin{matrix} {\dot{Γ}}_{1}^{'} \end{matrix}$ 、 $\begin{matrix} {\dot{Γ}}_{2}^{'} \end{matrix}$ 以及 $\begin{matrix} {\dot{Γ}}_{3}^{'} \end{matrix}$ 的相关表达式。

基于Schur补性质, 将 $\begin{matrix} \dot{A} \end{matrix}$ =A+α I, $\begin{matrix} \dot{B} \end{matrix} \begin{matrix} \dot{K} \end{matrix}$ =exp(α τ ₂(t)) $\begin{matrix} \dot{B} \end{matrix} \begin{matrix} \dot{K} \end{matrix}$ , $\begin{matrix} {\dot{E}}_{f} \end{matrix}$ =exp(α τ ₂(t))E_f, $\begin{matrix} \overset{̅}{K} \end{matrix}$ =exp(α τ ₂(t)) $\begin{matrix} \dot{P} \end{matrix}$ BK(K=( $\begin{matrix} \dot{P} \end{matrix} \begin{matrix} \dot{B} \end{matrix}$ )^-¹ $\begin{matrix} \overset{̅}{K} \end{matrix}$ ),

$\begin{matrix} \overset{̅}{F} \end{matrix}$ =exp(α τ ₂(t)) $\begin{matrix} \dot{P} \end{matrix}$ BF(F=( $\begin{matrix} \dot{P} \end{matrix} \begin{matrix} \dot{B} \end{matrix}$ )^-¹ $\begin{matrix} \overset{̅}{F} \end{matrix}$ )代入式(47), 可得定理2中的式(29)。

从0到+∞ , 对式(44)的两端做积分可得:

V(+∞ )-V(0)≤ $\begin{matrix} \int_{0}^{+} \end{matrix}$ (-η ^T(s)η (s))ds+ $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix} \begin{matrix} \int_{0}^{+} \end{matrix}$ ( $\begin{matrix} {d^{T}}_{α} \end{matrix}$ (s)d_α(s))ds+ $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix} \begin{matrix} \overset{\infty}{\sum_{k = 0}} \end{matrix}$ (t_k+₁-t_k)×

( $\begin{matrix} {e^{T}}_{η} \end{matrix}$ (t_k)e_η(t_k)+ $\begin{matrix} {e^{T}}_{f_{α}} \end{matrix}$ (t_k) $\begin{matrix} e_{f_{α}} \end{matrix}$ (t_k)) (48)

在零初始条件下, V(0)=0, V(+∞ )> 0, 可得:

$\begin{matrix} \int_{0}^{+} \end{matrix}$ (η ^T(s)η (s))ds≤ $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix} \begin{matrix} \int_{0}^{+} \end{matrix}$ ( $\begin{matrix} {d^{T}}_{α} \end{matrix}$ (s)d_α(s))ds+ $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix} \begin{matrix} \overset{\infty}{\sum_{k = 0}} \end{matrix}$ (t_k+₁-t_k)( $\begin{matrix} {e^{T}}_{η} \end{matrix}$ (t_k)e_η(t_k)+ $\begin{matrix} {e^{T}}_{f_{α}} \end{matrix}$ (t_k) $\begin{matrix} e_{f_{α}} \end{matrix}$ (t_k))(49)

即: $\begin{matrix} = η (t) =_{2}^{2} \end{matrix}$ ≤ $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix} \begin{matrix} = d_{α} (t) =_{2}^{2} \end{matrix}$ + $\begin{matrix} {\dot{γ}}_{1}^{2} \end{matrix} \begin{matrix} \overset{\infty}{\sum_{k = 0}} \end{matrix}$ (t_k+₁-t_k) $\begin{matrix} (= e_{η} (t_{k}) =_{2}^{2} + = e_{f_{α}} (t_{k}) =_{2}^{2}) \end{matrix}$ 。

在零初始条件下, 考虑下面的H₂性能指标:

J₂=V(η (t))- $\begin{matrix} \int_{0}^{t} \end{matrix}$ ( $\begin{matrix} {d^{T}}_{α} \end{matrix}$ (s)d_α(s))ds- $\begin{matrix} \overset{int (t)}{\sum_{k = 0}} \end{matrix}$ (t_k+₁-t_k)( $\begin{matrix} {e^{T}}_{η} \end{matrix}$ (t_k)e_η(t_k)+ $\begin{matrix} {e^{T}}_{f_{α}} \end{matrix}$ (t_k) $\begin{matrix} e_{f_{α}} \end{matrix}$ (t_k)+ $\begin{matrix} {v^{T}}_{α} \end{matrix}$ (t_k)v_α(t_k)) (50)

当d_α(t)≠ 0, e_η(t_k)≠ 0时, 可得

J₂=V(η (t))-V(η (0))- $\begin{matrix} \int_{0}^{t} \end{matrix}$ ( $\begin{matrix} {d^{T}}_{α} \end{matrix}$ (s)d_α(s))ds- $\begin{matrix} \overset{int (t)}{\sum_{k = 0}} \end{matrix}$ (t_k+₁-t_k)( $\begin{matrix} {e^{T}}_{η} \end{matrix}$ (t_k)e_η(t_k)+ $\begin{matrix} {e^{T}}_{f_{α}} \end{matrix}$ (t_k) $\begin{matrix} e_{f_{α}} \end{matrix}$ (t_k)) (51)

由Lyapunov函数和式(51)可得:

η ^T(t_k) $\begin{matrix} \dot{P} \end{matrix}$ η (t_k)≤ V(η (t))≤ $\begin{matrix} \int_{0}^{t} \end{matrix}$ ( $\begin{matrix} {d^{T}}_{α} \end{matrix}$ (s)d_α(s))ds+ $\begin{matrix} \overset{int (t)}{\sum_{k = 0}} \end{matrix}$ (t_k+₁-t_k)( $\begin{matrix} {e^{T}}_{η} \end{matrix}$ (t_k)e_η(t_k)+ $\begin{matrix} {e^{T}}_{f_{α}} \end{matrix}$ (t_k) $\begin{matrix} e_{f_{α}} \end{matrix}$ (t_k))(52)

通过定理2中的式(31)和Schur补引理, 可得:

$\begin{matrix} [\begin{matrix} \dot{P} & C^{T} \\ C & {\dot{γ}}_{2}^{2} I \end{matrix}] \end{matrix}$ ≥ 0⇔ $\begin{matrix} \dot{P} \end{matrix}$ - $\begin{matrix} \frac{1}{{\dot{γ}}_{2}^{2}} \end{matrix}$ C^TC> 0⇔ C^TC< $\begin{matrix} {\dot{γ}}_{2}^{2} \end{matrix} \begin{matrix} \dot{P} \end{matrix}$ (53)

由y_α(t)的表达式, 由式(52)和式(53)可得:

$\begin{matrix} {y^{T}}_{α} \end{matrix}$ (t)y_α(t)=η ^T(t_k)C^TCη (t_k)< $\begin{matrix} {\dot{γ}}_{2}^{2} \end{matrix} \begin{matrix} \int_{0}^{t} \end{matrix}$ ( $\begin{matrix} {d^{T}}_{α} \end{matrix}$ (s)d_α(s))ds+ $\begin{matrix} {\dot{γ}}_{2}^{2} \end{matrix} \begin{matrix} \overset{int (t)}{\sum_{k = 0}} \end{matrix}$ (t_k+₁-t_k)( $\begin{matrix} {e^{T}}_{η} \end{matrix}$ (t_k)e_η(t_k)+ $\begin{matrix} {e^{T}}_{f_{α}} \end{matrix}$ (t_k)× $\begin{matrix} e_{f_{α}} \end{matrix}$ (t_k))≤ $\begin{matrix} {\dot{γ}}_{2}^{2} \end{matrix} \begin{matrix} \int_{0}^{\infty} \end{matrix}$ ( $\begin{matrix} {d^{T}}_{α} \end{matrix}$ (s)d_α(s))ds+ $\begin{matrix} {\dot{γ}}_{2}^{2} \end{matrix} \begin{matrix} \overset{\infty}{\sum_{k = 0}} \end{matrix}$ (t_k+₁-t_k)( $\begin{matrix} {e^{T}}_{η} \end{matrix}$ (t_k)e_η(t_k)+ $\begin{matrix} {e^{T}}_{f_{α}} \end{matrix}$ (t_k) $\begin{matrix} e_{f_{α}} \end{matrix}$ (t_k))(54)

即, 当t> 0时, 广义H₂性能指标 $\begin{matrix} = y_{α} (t) =_{\infty} \end{matrix}$ ≤ $\begin{matrix} {\dot{γ}}_{2} \end{matrix} \begin{matrix} = d_{α} (t) =_{2} \end{matrix}$ + $\begin{matrix} {\dot{γ}}_{2} \end{matrix} \begin{matrix} \overset{\infty}{\sum_{k = 0}} \end{matrix}$ (t_k+₁-t_k)( $\begin{matrix} = e_{η} (t_{k}) =_{2} \end{matrix}$ + $\begin{matrix} = e_{f_{α}} (t_{k}) =_{2} \end{matrix}$ )是成立的。

系统中的执行器同时还受到饱和约束, 下面将对执行器饱和约束的线性域条件进行一些相关的变换ε ( $\begin{matrix} \dot{P} \end{matrix}$ )⊂ $\begin{matrix} \overset{̅}{l} \end{matrix}$ ( $\begin{matrix} \dot{F} \end{matrix}$ )⇔ | $\begin{matrix} f_{\dot{l}} \end{matrix}$ x|≤ 1, ∀ x∈ ε ( $\begin{matrix} \dot{P} \end{matrix}$ )。其中, $\begin{matrix} \dot{l} \end{matrix}$ ∈ [1, m], $\begin{matrix} f_{\dot{l}} \end{matrix}$ 是 $\begin{matrix} \dot{F} \end{matrix}$ 的第 $\begin{matrix} \dot{l} \end{matrix}$ 行且

⇔ $\begin{matrix} {\dot{f}}_{j} \end{matrix} \begin{matrix} {\dot{P}}^{- 1} \end{matrix} \begin{matrix} {\dot{f}}^{T}_{j} \end{matrix}$ ≤ 1(55)

基于Schur补引理, 可得:

⇔ $\begin{matrix} [\begin{matrix} 1 & f_{\dot{l}} {\dot{P}}^{- 1} \\ * & {\dot{P}}^{- 1} \end{matrix}] \end{matrix}$ ≥ 0, $\begin{matrix} \dot{l} \end{matrix}$ ∈ [1, m] (56)

设 $\begin{matrix} f_{\dot{l}} \end{matrix} \begin{matrix} {\dot{P}}^{- 1} \end{matrix}$ = $\begin{matrix} {\overset{̅}{f}}_{\dot{l}} \end{matrix}$ , 所以式(56)等价于定理2中的式(32), 证毕。

4 仿真实验与分析

为了验证文中理论结果的有效性与正确性, 采用四容水箱基准实例^[12]来完成相关的仿真实验, 模型中的相关参数为:

$\begin{matrix} [\begin{matrix} - 0.016 & 0 & 0.042 & 0 \\ 0 & - 0.011 & 0 & 0.033 \\ 0 & 0 & - 0.042 & 0 \\ 0 & 0 & 0 & - 0.033 \end{matrix}] \end{matrix}$

B= $\begin{matrix} [\begin{matrix} 0.083 & 0 \\ 0 & 0.063 \\ 0 & 0.048 \\ 0.031 & 0 \end{matrix}] \end{matrix}$ , E_d= $\begin{matrix} [\begin{matrix} 0.01 \\ 0.01 \\ 0 \\ 0.01 \end{matrix}] \end{matrix}$

C=diag{0.5 0.5 0.5 0.5}

D_v=[0.01 0 0.01 0.01]^T

f(t)= $\begin{matrix} \{\begin{matrix} 0, & t \leq 100 \\ 2 + 2 \sin 0.01 π (t - 100), & 100 < t \leq 800 \end{matrix} \end{matrix}$

其中, 模型的参数满足假设中的相关条件rank(B, E_f)=rank(B), 水箱由两个泵供水。控制输入u(t)为水泵的电压值, 并假设故障发生在第一个输入通道E_f=-[0.083 0 0 0.031]^T, x₁(t)、x₂(t)、x₃(t)、x₄(t)分别表示4个水箱的相关水位, y₁(t)、y₂(t)、y₃(t)、y₄(t)分别表示对相关量的观测。假设噪声d(t)和v(t_k)是零均值方差为0.01的白噪声过程和序列, 且x₀=[4 4 2 2]^T。设n₁=1.2, n₂=0.9, n₃=0.5, h=0.1, 由定理1可得:

L= $\begin{matrix} [\begin{matrix} 39.9304 & 61.3353 & 57.2196 & - 98.3081 \\ 0.6741 & 3.1507 & 1.0409 & - 1.7594 \\ 0.8787 & 0.9782 & 1.8524 & - 2.1734 \\ 15.2179 & 24.4634 & 22.1184 & - 37.4910 \end{matrix}] \end{matrix}$ ,

F=[-296.9266 -388.9586 -431.6723 718.2575],

γ _1min=2.3687。

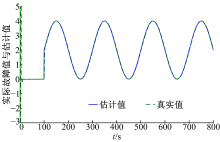
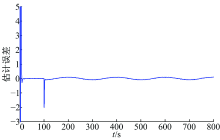
连续时变故障的估计效果与误差如图2、图3所示。

	Figure Option View Download New Window
	图2 连续时变故障及其估计值的变化趋势Fig.2 Trend of variation of continuous time-varying failure and its estimated value

	Figure Option View Download New Window
	图3 故障估计值的误差变化Fig.3 Variation of error for estimated failure value

从图2和图3可以看出, 基于定理1设计出的故障观测器可以实现对执行器连续时变故障的一个准确估计, 而且故障估计值的误差变化较小。采用本文Lyapunov函数所得的观测器较文献[12]在估计故障时具有更小的误差, 除了在误差发生瞬间的误差稍大外, 其余时刻均能保持在± 0.01之内, 而在文献[12]中除了误差发生瞬间其余时刻的误差都将大于0.01, 说明定理1提供的观测器具有更小的误差。接下来, 将设计非均匀传输主动容错控制器, 根据(I-BB⁺)E_f=0, 可得:

B⁺= $\begin{matrix} [\begin{matrix} 11.9550 & - 10.5732 & 0 & 0.2469 \\ 0 & 0 & 0 & 0 \end{matrix}] \end{matrix}$

当连续时变故障被准确估计出来后, 采用定理2中的非均匀传输主动容错控制器来进行调节, 对相关参数作如下规定, h=0.1, n₁=1.0, n₂=0.92, n₃=0.1, m₁=0.1, m₂=0.1, m₃=0.1, $\begin{matrix} \overset{̅}{h} \end{matrix}$ =1.0, α =0.2, $\begin{matrix} {\tilde{γ}}_{1} \end{matrix}$ =1.7, $\begin{matrix} {\tilde{γ}}_{2} \end{matrix}$ =1.7, δ =0.001, Υ ₁=[1 0; 0 0], Υ ₂=[0 0; 0 1]。协同求出具有故障调节能力的状态反馈控制器和事件触发器分别为

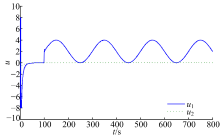
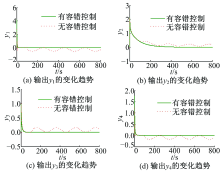
K= $\begin{matrix} [\begin{matrix} 3.4359 & 0.0003 & 0.5535 & - 0.0077 \\ 0.5713 & 0.0006 & 1.0668 & 0.0063 \end{matrix}] \end{matrix}$ ,

Φ =diag{76.0260 76.0260 76.0260 76.0260}在K、B⁺和Φ 的共同作用下, 系统(12)的控制输入和输出 (分未加/加故障调节两种情形)如图4、图5所示。

	Figure Option View Download New Window
	图4 系统控制输入的变化趋势Fig.4 Trend of variation of control input

图5给出了两种情形下系统的输出曲线, 可以看出:在系统发生故障时, 如果控制器无容错能力, 则系统的输出将会产生较大的波动, 而采用控制律(11)和定理2给出的方法所设计的非均匀传输主动容错控制器时, 即使系统执行器受到

	Figure Option View Download New Window
	图5 闭环故障系统的输出趋势Fig.5 Trend of output for closed-loop system

饱和约束(见图4), 也同样能确保故障系统具有良好的性能。由于在控制器设计时, 考虑了α -稳定性、H₂/H_∞性能, 因此较文献[12]具有更加满意的容错性能。

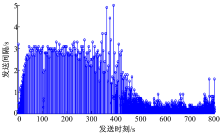
网络化闭环故障系统(12)在DETCS下的数据发送情况如图6所示。

	Figure Option View Download New Window
	图6 故障系统的数据发送情况Fig.6 Data transmission circumstance of failure system

可以看出, 当系统中引入了DETCS后, 对于通信触发参数选为δ =0.01时, 较由时钟驱动的PTTCS 800 s内发送8000个数据而言, DETCS下仅需发送2178个数据, 节约了大量的网络通信资源, 而且同时也保证了闭环故障系统具有良好的性能。

当为事件触发参数选取不同的值时, 仍取800 s的仿真时段, PTTCS发送的数据量为8000个, 具有容错能力的NCS数据发送情况如表1所示。

从表1可以看出, 随着事件触发参数的变大, 平均发送周期h_av将随之变大, 而数据发送量n和数据发送率r_e/t将随之变小。这也揭示出通过调节事件触发参数可以实现在系统控制质量和网络服务质量之间的满意折中平衡。

表1 不同事件触发参数下系统数据的发送情况α =0.2 Table 1 System data transmission circumstances under different event triggered parameter α =0.2

5 结束语

针对具有执行器饱和约束与时变故障的NCS, 本文研究了此类系统的满意主动容错控制与网络通信间的协同设计问题, 提出了DETCS下主动容错的架构与设计理念。通过应用非均匀采样系统的研究方法, 将DETCS下NCS中的非均匀传输周期对系统性能的影响转化为对系统时滞的影响。基于Lyapunov理论和线性凸组合理论, 先在等采样周期下通过采用状态观测器给出了具有H_∞-性能的状态与故障估计方法; 进而又在非均匀传输周期下, 给出了同时满足α -稳定性、H₂-性能、H_∞-性能的满意主动容错控制器与DETCS中事件触发矩阵的协同求解方法。采用四容水箱基准实例进行仿真实验, 结果表明本文方法不仅较以往文献能够更加准确地估计故障, 而且可以使闭环故障NCS在具有良好动态性能(扰动抑制水平和峰值输出抑制水平)的前提下, 节约一定的网络通信资源, 从而兼顾NCS控制质量和网络服务质量的双重目标。在DETCS下, 研究非线性NCS的满意主动容错与网络通信间的协同设计问题将是下一步的研究重点。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Ding S X, Zhang P, Yin S. An integrated design framework of fault-tolerant wireless networked control systems for industry automatic control applications[J]. IEEE Transaction on Industrial Informatics, 2013, 9(1): 462-471. [本文引用:1]
[2]	Yang Chun-xi, Guan Zhi-hong, Huang Jian. Stochastic fault tolerant control of networked control systems[J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 2009, 346(10): 1006-1020. [本文引用:1]
[3]	Peng C, Yang T C, Tian E G. Robust fault-tolerant control systems with stochastic actuator failure[J]. IET Control Theory and Applications, 2010, 4(12): 3003-3011. [本文引用:1]
[4]	Mao Ze-hui, Jiang Bin, Shi Peng. Observer-based fault-tolerant control for a class of networked control systems with transfer delays[J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 2011, 348(4): 763-776. [本文引用:1]
[5]	Mahmud M S, Memo A M. Observer-based fault-tolerant control for a class of nonlinear networked control systems[J]. International Journal of Control, 2014, 87(8): 1707-1715. [本文引用:1]
[6]	Wang X F, Lemmon M D. Event-triggering in distributed networked control systems[J]. IEEE Transactions on Automatic Control, 2011, 56(3): 586-601. [本文引用:1]
[7]	Yue Dong, Tian En-gang, Han Qing-Long. A delay system method for designing event-triggered controllers of networked control systems[J]. IEEE Transactions on Automatic Control, 2013, 58(2): 475-481. [本文引用:1]
[8]	Wang H J, Shi P, Agarwal R K. Network-based event-triggered filtering for markovian jump systems[J]. International Journal of Control, 2016, 89(6): 1096-1110. [本文引用:1]
[9]	Liu Jin-liang, Yue Dong. Event-triggering in networked systems with probabilistic sensor and actuator faults[J]. Information Sciences, 2013, 240: 145-160. [本文引用:1]
[10]	Duan Kai, Zhang Wei-dong. Event-triggered fault-tolerant control for networked systems with dynamic quantiser[J]. IET Control Theory and Applications, 2016, 10(9): 1088-1096. [本文引用:1]
[11]	曹慧超, 李炜. 离散事件触发不确定NNCS鲁棒容错控制[J]. 吉林大学学报: 工学版, 2015, 45(6): 1895-1905. Cao Hui-chao, Li Wei. Robust fault-tolerant control for uncertain NNCS with discrete event-triggered communication scheme[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(6): 1895-1905. [本文引用:1]
[12]	邱爱兵, 吉虹钢, 顾菊平. 非均匀采样数据系统时变故障估计与调节最优集成设计[J]. 自动化学报, 2014, 40(7): 1493-1504. Qiu Ai-bing, Ji Hong-gang, Gu Ju-ping. Optimal integrated design of time-varying fault estimation and accommodation for nonunniformly sampled data systems[J]. Acta Automatica Sinica, 2014, 40(7): 1493-1504. [本文引用:2]
[13]	Luo Xiao-yuan, Shang Mei-jie, Chen Cai-lian. Guaranteed cost active fault-tolerant control of networked control system with packet dropout and transmission delay[J]. International Journal of Automation and Computing, 2010, 7(4): 509-515. [本文引用:1]
[14]	肖会芹, 何勇, 吴敏. 基于T-S模糊模型的采样数据网络控制系统H_∞输出跟踪控制[J]. 自动化学报, 2015, 41(3): 661-668. Xiao Hui-qin, He Yong, Wu Min. H_∞output tracking control for sampled-data networked control systems in T-S fuzzy model[J]. Acta Automatica Sinica, 2015, 41(3): 661-668. [本文引用:1]
[15]	Fridman Emilla, Orlov Yury. Exponential stability of linear distributed parameter systems with time-varying delays[J]. Automatica, 2009, 45(1): 194-201 [本文引用:2]
[16]	Yang Fei-sheng, Zhang Hua-guang, Wang Ying-chun. An enhanced input-delay approach to sampled-data stabilization of T-S fuzzy systems via mixed convex combination[J]. Nonlinear Dynamics, 2014, 75(3): 501-512. [本文引用:1]
[17]	李炜, 申富媛. 具有α-稳定NCS满意容错设计[J]. 控制工程, 2013, 20(1): 149-154. Li Wei, Shen Fu-yuan. Satisfactory fault-tolerant design of NCS with α-stability[J]. Control Engineering of China, 2013, 20(1): 149-154. [本文引用:1]
[18]	谢徳晓, 韩笑冬, 黄鹤. 具有时延和丢包的网络化控制系统H_∞状态反馈控制[J]. 控制与决策, 2009, 24(4): 587-592. Xie De-xiao, Han Xiao-dong, Huang He. H_∞ state feedback control for networked control system with time-delay and packet dropout[J]. Control and Decision, 2009, 24(4): 587-592. [本文引用:1]
[19]	Zuo Zhi-qiang, Ho D W C, Wang Yi-jing. Fault-tolerant control for singular systems with actuator saturation and nonlinear perturbation[J]. Automatica, 2010, 46(3): 569-576. [本文引用:1]
[20]	Meng Zi-yang, Zhao Zhi-yun, Lin Zong-li. On global leader-following consensus of identical linear dynamic systems subject to actuator saturation[J]. Systems & Control Letters, 2013, 62(2): 132-142. [本文引用:1]

2013

0.0

... 0 引言随着现代网络化控制系统(Networked control systems, NCS)超复杂性和大规模性的日益突显,安全可靠性已经成为保证NCS正常运行的一项重要需求,这也促使了近几年来学术界对NCS的故障诊断与容错控制类问题的高度关注^[1,2,3],并取得了卓有成效的进展^[4,5] ...

2009

0.0

2010

0.0

2011

0.0

2014

0.0

2011

0.0

... 离散事件触发通信机制 (Discrete event-triggered communication scheme,DETCS)^[6,7,8],引入到了NCS的容错控制中^[9,10,11],并取得了良好的应用效果 ...

2013

0.0

... 离散事件触发通信机制 (Discrete event-triggered communication scheme,DETCS)^[6,7,8],引入到了NCS的容错控制中^[9,10,11],并取得了良好的应用效果 ...

2016

0.0

... 离散事件触发通信机制 (Discrete event-triggered communication scheme,DETCS)^[6,7,8],引入到了NCS的容错控制中^[9,10,11],并取得了良好的应用效果 ...

2013

0.0

... 离散事件触发通信机制 (Discrete event-triggered communication scheme,DETCS)^[6,7,8],引入到了NCS的容错控制中^[9,10,11],并取得了良好的应用效果 ...

2016

0.0

... 离散事件触发通信机制 (Discrete event-triggered communication scheme,DETCS)^[6,7,8],引入到了NCS的容错控制中^[9,10,11],并取得了良好的应用效果 ...

2015

0.0

. 2015, 45(6):1895-1905 DOI:10.13229/j.cnki.jdxbgxb201506025

Robust fault-tolerant control for uncertain NNCS with discrete event-triggered communication scheme

离散事件触发不确定NNCS鲁棒容错控制

Cao Hui-chao , Li Wei.

曹慧超, 李炜

College of Electrical and Information Engineering, Lanzhou University of Technology, Lanzhou 730050, China

First, a new model of uncertain nonlinear closed-loop fault Networked Control System(NCS) is established, which integrates the network time-varying delay, actuator saturation and fault, and the discrete event-triggered condition in a unified framework. Then, utilizing the Lyapunov stability theory and delay decomposition technology, combing the improved Jensen integral inequality and the reciprocal convex combination lemma, the delay- and event-dependent invariant set condition for ensuring closed-loop fault NCS stability is derived. The co-design method for both robust fault-tolerant controller and the weight matrix of discrete event-triggered conditions is given. Finally,a simulation case is employed to demonstrate that the proposed method, which guarantees faulty NCS based on Discrete Event-Triggered Communication Scheme(DETCS), possesses good fault-tolerant performance, and saves the limited network resources by reasonably choosing the triggering parameters.

首先建立了集网络时变时延、执行器饱和约束及故障、离散事件触发条件于一体的不确定非线性闭环故障网络化控制系统(NCS)模型。然后应用Lyapunov稳定性理论和时延分段技术,结合改进的Jensen积分不等式和互反凸组合引理,推证出了闭环故障NCS稳定的时滞且事件依赖不变集充分条件,并给出了鲁棒容错控制器与离散事件触发条件权矩阵的协同设计方法。最后,通过一个仿真算例验证了本文方法不仅能使基于离散事件触发通信机制(DETCS)的NCS对故障有效容错,而且可通过触发参数的适当选取来节省有限的网络资源。

... 离散事件触发通信机制 (Discrete event-triggered communication scheme,DETCS)^[6,7,8],引入到了NCS的容错控制中^[9,10,11],并取得了良好的应用效果 ...

2014

0.0

. 2014, 40(7):1493-1504 DOI:doi:10.3724/SP.J.1004.2014.01493

Optimal integrated design of time-varying fault estimation and accommodation for nonunniformly sampled data systems

非均匀采样数据系统时变故障估计与调节最优集成设计

Qiu Ai-bing , Ji Hong-gang , Gu Ju-ping.

邱爱兵, 吉虹钢, 顾菊平

In this paper, an active fault tolerant control design scheme is presented for a class of nonuniformly sampled data systems with continuous time-varying fault. Since the adaptive fault diagnosis technique can not be directly extended to such systems, an optimal continuous augmented observer is firstly designed to estimate the fault by use of nonuniform discrete output. The observer can not only guarantee fast convergence of estimation errors but also be robust to external disturbance. Then, an iterative algorithm is proposed to make a tradeoff between estimation delay and system robustness. Furthermore, with the obtained fault information, a nonuniformly sampled data fault tolerant controller based on state feedback is designed to recover the performance of the faulty system in consideration of the adverse impact of estimation errors and inter-sample behavior of continuous fault. Finally, the simulation results of an quadruple-tank example are included to illustrate the effectiveness of the proposed method.

针对一类发生连续时变故障的非均匀采样数据系统，建立了一套主动容错控制最优设计方案. 首先，为了实现基于非均匀离散采样输出对连续故障的估计，同时鉴于现有自适应故障诊断方法无法直接推广于非均匀采样数据系统，提出一种连续时间增广观测器最优设计方法，既能保证故障估计误差快速收敛同时又对外界干扰鲁棒；并且提出一个迭代算法对故障估计延迟与系统鲁棒性进行权衡；进一步地，基于所获得的故障信息，并考虑估计误差和时变故障内采样特性对容错控制带来的不利因素，设计基于状态反馈的非均匀采样容错控制器来快速恢复故障系统性能；最后，通过对四容水箱基准实例的仿真来验证所提方法的有效性.

... 在实际应用中,主动容错控制在处理不同类型故障时不仅具有灵活性高与性能更优等特点,而且其控制器设计的保守性也要明显小于被动容错的情形^[12,13] ...

... 4 仿真实验与分析为了验证文中理论结果的有效性与正确性,采用四容水箱基准实例^[12]来完成相关的仿真实验,模型中的相关参数为: ...

2010

0.0

2015

0.0

. 2015, 41(3):661-668 DOI:10.16383/j.aas.2015.c140444

H_#cod#x0221e;output tracking control for sampled-data networked control systems in T-S fuzzy model

基于T-S模糊模型的采样数据网络控制系统H #cod#x0221e; 输出跟踪控制

Xiao Hui-qin , He Yong , Wu Min.

肖会芹, 何勇, 吴敏

1. School of Information Science and Engineering, Central South University, Changsha 410083; 2. School of Automation, China University of Geosciences, Wuhan 430074; 3. College of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou 412008

This paper studies the problem of H ∞ output tracking control for sampled-data networked control systems in T-S (Takagi-Sugeno) fuzzy model. By using input-delay and parallel distributed compensation (PDC) techniques, an augment tracking model based on T-S fuzzy model is firstly established,in which the sampling period of the sampler, signal transmission delay and data packet dropouts are transformed to the refreshing interval of a zero-order holder. Furthermore, Lyapunov method is employed to derive several su±cient criteria ensuring the prescribed H ∞ tracking performance. Meanwhile, a fuzzy controller design is also presented. Finally, a numerical example is given to illustrate that the designed fuzzy controller can realize good tracking.

研究具有采样数据的基于T-S (Takagi-Sugeno) 模糊模型网络控制系统 H ∞ 输出跟踪控制问题. 提出将采集器端数据采样周期、数据传输时滞和数据丢包转换为零阶保持器端数据更新周期, 在此基础上, 利用输入时滞法和PDC (Parallel distributed compensation) 技术, 建立网络环境下被控对象和参考模型合并的基于T-S 模糊模型的增广系统模型. 通过Lyapunov 方法, 并充分利用采样特性, 给出系统实现 H ∞ 输出跟踪的充分条件, 以及可靠模糊控制器的设计. 仿真结果表明所设计模糊控制器能够实现该类系统良好的跟踪.

... 采样系统的研究方法主要有3类^[14]:一是先对连续对象进行离散化,应用离散系统控制理论进行系统设计 ...

2009

0.0

... 三是将非均匀采样周期对系统的影响转化为对系统时滞的影响,应用时滞系统中成熟的理论^[15]研究此类问题 ...

... 可以看到:经由智能传感单元,采样器1输出的信号为等物理周期的离散信号,由于在一个采样周期中信号的幅值保持不变,则在相邻的采样时刻间可借助于时滞系统理论^[15]为采样数据NCS(1)设计状态和故障观测器 ...

2014

0.0

... 其中,第三类方法因无需对连续的系统对象进行离散化,也无需对控制器进行特殊处理,受到了较多的关注^[16],但其保守性亦是不可忽视的问题 ...

2013

0.0

... 仅从容错控制系统的性能而言,NCS不仅需要保证故障系统具有最基本的稳定性能,还需要系统具有一些其他的良好动态性能^[17,18](如#cod#x003b1 ...

2009

0.0

. 2009, 24(4):587-592

H_#cod#x0221e; state feedback control for networked control system with time-delay and packet dropout

具有时延和丢包的网络化控制系统H #cod#x0221e; 状态反馈控制

Xie De-xiao , Han Xiao-dong , Huang He.

谢徳晓, 韩笑冬, 黄鹤

研究了具有时延和数据包丢失的网络控制系统 H ∞ 状态反馈控制问题.考虑了网络控制系统中同时存在时延和数据包丢失的情况,将丢包过程建模为有限状态的马尔可夫过程.在此模型的基础上,利用Lyapunov稳定性理论和线性矩阵不等式方法,给出了保持系统均方稳定且满足 H ∞ 性能的控制器存在的充分条件,并给出了相应的设计方法.最后数例仿真结果表明了控制器设计方法的有效性.

... 仅从容错控制系统的性能而言,NCS不仅需要保证故障系统具有最基本的稳定性能,还需要系统具有一些其他的良好动态性能^[17,18](如#cod#x003b1 ...

2010

0.0

... 在控制系统中,执行器所受到的饱和约束对系统的影响亦是不容忽视的^[19,20] ...

2013

0.0

... 在控制系统中,执行器所受到的饱和约束对系统的影响亦是不容忽视的^[19,20] ...