基于贝叶斯网络的电子节气门电磁敏感度评估

引用本文

孙晓颖, 王震, 杨锦鹏, 扈泽正, 陈建. 基于贝叶斯网络的电子节气门电磁敏感度评估[J].吉林大学学报（工学版）, 2018,48(1): 281-289
SUN Xiao-ying, WANG Zhen, YANG Jin-peng, HU Ze-zheng, CHEN Jian. Electromagnetic susceptibility assessment of electronic throttle based on Bayesian network[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 281-289 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161343
Permissions

基于贝叶斯网络的电子节气门电磁敏感度评估

孙晓颖, 王震, 杨锦鹏, 扈泽正, 陈建

吉林大学通信工程学院,长春 130022

通讯作者：陈建(1977-),男,副教授,博士. 研究方向:汽车电磁兼容,信号处理. E-mail:chenjian@jlu.edu.cn

作者简介:孙晓颖(1969-),男,教授,博士生导师. 研究方向:汽车电磁兼容,无线定位技术及应用.E-mail:sunxy@jlu.edu.cn

基金:装备预先研究项目(30105030302).

摘要

针对电子节气门电磁脉冲效应试验中诸多不确定性导致有限样本下评估不准确的问题,研究了基于贝叶斯网络(BN)的敏感度评估方法,通过从概率角度考虑所有不确定参量来提高评估准确性。首先,建立节气门系统故障树(FT)模型,采用电磁拓扑(EMT)分析系统电磁耦合途径。然后,建立融合故障树和电磁拓扑的电磁敏感度贝叶斯网络评估模型,并给出模型各节点概率计算方法。最后,以高空电磁脉冲(HEMP)为例描述了电子节气门电磁敏感度评估模型输入数据获取方法和模型计算过程,验证了模型的有效性。

关键词: 通信技术; 系统评估与可行性分析; 有意电磁干扰; 高空电磁脉冲; 发动机电子节气门; 敏感度评估; 贝叶斯网络

中图分类号:N945.17 文献标志码:A 文章编号:1671-5497(2018)01-0281-09

Electromagnetic susceptibility assessment of electronic throttle based on Bayesian network

SUN Xiao-ying, WANG Zhen, YANG Jin-peng, HU Ze-zheng, CHEN Jian

College of Communication and Engineering, Jilin University, Changchun 130022, China

Abstract

A modeling and parameter determining method is proposed based on Bayesian Networks (BN) for electronic throttle susceptibility assessment of Intentional Electromagnetic Interference (IEMI). This method can remedy the deficiencies of susceptibility assessment based on effect test. First, according to the structure of electronic throttle control system, the Fault Tree (FT) model is built. The coupling of the system with IEMI is analyzed using Electromagnetic Topology (EMT). Then, the BN assessment model is built to integrate the FT and EMT, and the probability acquiring of BN nodes is discussed. As data input of assessment model, the susceptibilities of components are tested with pulse voltage injection, and the Electromagnetic Stress (EMS) of the components is simulated using CST CABLE STUDIO. Finally, the electronic throttle susceptibility assessment against High-altitude Electromagnetic Pulse (HEMP) is taken as an example to illustrate the modeling and probability calculation process, which verify the effectiveness of the BN based assessment model.

Keyword: communication technology; systematic evaluation and feasibility analysis; intentional electro-magnetic interference (IEMI); high-altitude electro-magnetic pulse (HEMP); engine electronic throttle; susceptibility assessment; Bayesian networks

Show Figures

0 引言

电磁脉冲(Electromagnetic pulse, EMP)等有意电磁干扰(Intentional electromagnetic interference, IEMI)严重威胁了车辆机动性和行驶安全性^[1]。电子节气门(Electronic throttle, ET)控制着进入气缸的空气量, 其工作异常将导致发动机喘振和熄火等故障发生。研究电子节气门电磁敏感度评估方法对确定发动机系统敏感零部件及电磁防护设计具有重要意义。

目前电磁脉冲效应的研究, 主要采用试验方法获得电子系统的效应类型和敏感度阈值^{[1, 2, 3, 4]}。由于试验条件和成本的限制, 试验样本有限, 试验结论不具备很强的外推性^[5]。受电磁环境、耦合通道、器件敏感度等因素影响, 电子系统电磁敏感度分析中存在诸多不确定性, 如电磁波不同的入射方向和极化方向、子系统或设备不同的安装位置、同一器件敏感度为非定值等。因此, 电子系统电磁敏感度评估更适合采用不确定性的分析方法。

具有代表性的不确定性评估方法主要有故障树分析(Fault tree analysis, FTA)方法^{[6, 7, 8]}和贝叶斯网络(Bayesian networks, BN)分析方法^{[9, 10]}。FTA方法广泛应用于系统可靠性和安全性分析, 但在评估系统电磁敏感度时存在以下不足:①对于一些复杂系统, 导致顶事件的基本事件较多, 造成基于最小割集布尔运算的计算十分复杂^[9]; ②故障树(Fault tree, FT)模型中不包含导致故障发生的电磁环境和电磁应力分析^[10], 无法完整描述电磁波与系统相互作用的全过程; ③系统电磁效应有功能正常、逻辑紊乱和硬件损伤3种状态^[11], 而故障树分析中只包含两种逻辑状态, 对于多故障状态需要特殊对待。贝叶斯网络是一种基于图论和概率论的二元体, 具有较强的建模能力, 可以很好地描述电磁波对电子系统干扰效应全过程, 有效克服了故障树分析方法的不足。文献[10]中提出了电子系统电磁易损性评估的贝叶斯网络框架, 将FT和电磁拓扑(Electro-magnetic topology, EMT)等工具有效融合在BN中, 为电子系统电磁易损性评估提供了更加有力的分析工具。

本文将贝叶斯网络分析方法应用于电子节气门电磁敏感度评估中。结合故障树和电磁拓扑分析建立了节气门电磁敏感度BN评估模型, 给出了模型计算方法; 并以高空电磁脉冲(High-altitude electromagnetic pulse, HEMP)环境为例验证了模型的有效性。本文方法涵盖了电磁脉冲与电子节气门相互作用过程中所有电磁耦合途径和系统失效途径, 有效解决了诸多不确定参量下辐射试验外推性差、评估不准确的难题。

1 节气门电磁效应分析

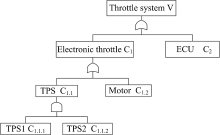
电子节气门由电机(Motor)和节气门位置传感器(Throttle position sensor, TPS)两部分组成。通过电机控制节气门开度实现目标进气量。位置传感器将节气门开度反馈给电控单元(Electronic control unit, ECU)实现闭环控制, 包含TPS1和TPS2 两个传感器。电子节气门控制系统组成如图1所示。

	Figure Option View Download New Window
	图1 电子节气门控制系统组成Fig.1 Structure of electronic throttle control system

电磁脉冲对车辆装备的损伤效应主要分为工作失灵和功能损坏^[1]。对电子节气门而言, 电磁脉冲可对电机和TPS产生干扰, 导致节气门进气量偏离目标值; 或者使电机停止工作, 暂时失效, 节气门进气量为零; 甚至通过热或电击穿, 使电机和TPS永久失效, 节气门损坏。

电磁脉冲进入电子系统的途径有两种:①前门耦合, 通过天线耦合进入系统; ②后门耦合, 通过孔缝、线缆等耦合进入系统。电子节气门的电磁耦合途径属于后门耦合, 如图2所示。

车身金属壳体上存在大量孔缝, 如散热器孔洞、发动机舱盖与车身缝隙等。电磁脉冲传播到车身和孔缝附近, 会发生电磁散射和穿透。不同频率波分量穿透孔缝的能力不同, 导致电磁波在发动机舱内产生共振效应; 孔缝附近电磁波产生增强效应, 使耦合场强于入射场^[12]。这意味着发动机舱内部V₁电磁场分布比发动机舱外部V₀更复杂。

	Figure Option View Download New Window
	图2 电子节气门电磁耦合模型Fig.2 Electromagnetic coupling model of electronic throttle

电子节气门为金属体, 但内部电路塑料外壳和线束插头等孔洞给电磁波渗透提供了途径。发动机舱V₁内电磁波通过孔洞耦合进入电子节气门V_{2, 1}内部, 对电子元器件产生辐射干扰。此外, 电子节气门通过线缆与发动机电控单元连接。这些线缆拾取发动机舱V₁内电磁能量, 以瞬态高电压和大电流的形式传导到终端负载, 对节气门电子器件产生传导干扰^[13]。可见, 电子节气门电磁脉冲效应由电磁场辐射干扰和线缆传导干扰共同作用引起。

2 贝叶斯网络评估模型

电磁波通过层层渗透作用在零部件上造成零部件受扰, 最终导致节气门控制系统发生故障。利用EMT 和 FT模型分别描述电磁渗透过程及节气门失效过程, 建立融合FT 和 EMT 的 BN评估模型。

2.1 FT 模型

节气门开度控制包括信息采集、状态判断和指令控制3个步骤。涉及到的结构有TPS、ECU和电机。TPS和ECU之间, 电机与ECU之间都是通过1~2 m长线缆进行连接。TPS1、TPS2将节气门开度信息通过线缆传给ECU, ECU对发动机状态进行判断确定节气门目标开度, 然后输出控制信号通过线缆驱动电机来调节节气门开度。中间任何一个环节出现故障都会导致节气门开度偏离目标开度。这就意味着它们在FT模型中是“ 或” 的逻辑关系。TPS和电机是节气门的组成部分, 可以把两者的故障归类于节气门故障。TPS1和TPS2采用冗余设计, 两者同时失效才判定为节气门开度信息采集异常, 因此TPS1、TPS2在故障树中是“ 与” 的逻辑关系。电子节气门控制系统 FT 模型和各层次编号如图3所示。

	Figure Option View Download New Window
	图3 电子节气门控制系统FT模型Fig.3 FT model of electronic throttle control system

故障树结构函数如式(1)所示:

P(V)= $\begin{matrix} \overset{2}{\sum_{i = 1}} \end{matrix}$ P_i= $\begin{matrix} \overset{2}{\sum_{m = 1}} \end{matrix}$ P₁_.m+P₂(1)

式中:P_i是C_i的故障概率, i=1, 2; P₁_.m是对应 $\begin{matrix} {C_{1 .}}_{m} \end{matrix}$ 的故障概率, m=1, 2; P₁_.₁=P₁_.₁_.₁· P₁_.₁_.₂。

2.2 耦合途径EMT分析

采用EMT理论对电磁耦合途径进行分析, 考虑包括辐射和传导在内的所有耦合途径, 最终确定主要耦合通道。参照文献[14]中EMT表示方法, 将发动机舱外部和内部分别用V₀和V₁表示, 节气门体和电控单元壳体分别用V_{2, 1}和V_{2, 2}表示。各电子器件都受到渗透进壳体内的电磁场辐射影响。为了表示V₁内线缆的传导干扰, 将连接节气门和ECU的线束用L₁、L₂表示。节气门控制系统EMT和各器件编号如图4所示。

	Figure Option View Download New Window
	图4 电子节气门控制系统EMTFig.4 EMT of electronic throttle control system

EMP穿过发动机舱体时能量密度被削减, 加上节气门体和电控单元壳体的屏蔽作用, 辐射干扰的作用已经很小, 电磁干扰主要由线缆传导耦合引入。因此, 线束L₁、L₂视为电子节气门电磁耦合的主要通道。

2.3 BN 评估模型

结合FT分析和EMT分析, 建立电子节气门电磁敏感度BN 评估模型, 如图5所示。节点代表自由场和实体结构。箭头表示从环境到电磁应力(Electromagnetic stress, EMS), 从零部件到系统的因果关系。FT和EMT结合处表示电子器件经受的电磁应力。BN评估模型展示了所有可能的电磁耦合途径和系统失效途径, 同时兼顾了辐射和传导两种电磁干扰的测试和计算。

	Figure Option View Download New Window
	图5 BN敏感度评估模型Fig.5 BN model of susceptibility assessment

3 BN模型计算

系统的电磁干扰效应是不确定的, 而是概率事件, 需从概率论角度进行描述。节气门控制系统失效概率与系统V和IEMI两个因素有关。用联合概率表示为:

P_V=P_V $\begin{matrix} (V, IEMI) \end{matrix}$ (2)

在BN的基础上, 因果关系可以用条件概率来表示, 即:

P_V $\begin{matrix} (V, IEMI) \end{matrix}$ =P_V $\begin{matrix} (V| IEMI) \end{matrix}$ P $\begin{matrix} (IEMI) \end{matrix}$ (3)

式(3)表示系统V 在IEMI 干扰下的辐射敏感概率。采用IEMI 环境进行试验对实验条件要求很高。可以从IEMI 环境出发, 结合器件敏感度利用BN 层层分析系统故障概率。IEMI 在系统周围产生的电磁环境(Ambient electromagnetic environment, AEME)对电机和TPS 产生电磁应力(Stres)导致器件失效(Comp), 最终导致节气门故障(Subs)和控制系统(V)功能故障。这个过程是串联的因果关系, 可以用式(4)表示:

P_V(V, AEME)=P( $\begin{matrix} V| \end{matrix}$ Subs)P(Subs $\begin{matrix} |Comp \end{matrix}$ )×

P(Comp, Stres)P(Stres $\begin{matrix} |AEME \end{matrix}$ )×

P(AEME $\begin{matrix} |IEMI \end{matrix}$ )P(IEMI)(4)

下面将详细介绍式(4)中各概率的计算方法。

3.1 P $\begin{matrix} (IEMI) \end{matrix}$ 计算

将IEMI分成K种类型, 每个子集S_k(k=1, 2, …, K)均对系统造成威胁, 采用全概率公式进行描述。各子集S_k符合下面条件:

$\begin{matrix} \{IEMI\} \end{matrix}$ = $\begin{matrix} \overset{K}{⋃_{k = 1}} \end{matrix}$ S_k, $\begin{matrix} \overset{K}{⋂_{k = 1}} \end{matrix} \begin{matrix} \{S_{k}\} \end{matrix}$ =∅(5)

每个子集被分配的概率P' $\begin{matrix} (S_{k}) \end{matrix}$ 由专家根据干扰源种类、距离和攻击持续时间确定, 然后对所有子集概率值进行归一化。

P $\begin{matrix} (S_{k}) \end{matrix}$ =P' $\begin{matrix} (S_{k}) \end{matrix} \begin{matrix} {(\overset{K}{\sum_{k = 1}} P' (S_{k}))}^{- 1} \end{matrix}$ (6)

P $\begin{matrix} (S_{k}) \end{matrix}$ 越大表明S_k类干扰源威胁越大。其中, P $\begin{matrix} (S_{k}) \end{matrix}$ =0, P $\begin{matrix} (S_{k}) \end{matrix}$ =1是两种极端情况, 分别表示无威胁和必然有威胁。在BN中所有概率值必须符合概率论基本公理, 所以P(S_k)=1(k=1, 2, …, K)是不允许的。

3.2 P $\begin{matrix} (AEME| IEMI) \end{matrix}$ 和P $\begin{matrix} (Stres| AEME) \end{matrix}$ 计算

如果有几个IEMI干扰源S_k(k=1, 2, …, K)同时到达系统, 可以表示为:

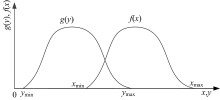
P $\begin{matrix} (AEME |IEMI) \end{matrix}$ = $\begin{matrix} \overset{K}{\sum_{i = 1}} \end{matrix}$ P $\begin{matrix} (AEME |S_{k}) \end{matrix}$ P $\begin{matrix} (S_{k}) \end{matrix}$ (7)

以一类IEMI源为例, 电磁波对器件产生的电磁应力可以用概率密度函数(Probability density function, PDF)g $\begin{matrix} (y) \end{matrix}$ 表示, 且g $\begin{matrix} (y) \end{matrix}$ 满足式(8):

$\begin{matrix} \int_{y_{\min}}^{y_{\max}} \end{matrix}$ g $\begin{matrix} (y) \end{matrix}$ dy=1, y∈ $\begin{matrix} [y_{\min}, y_{\max}] \end{matrix}$ (8)

P $\begin{matrix} (Stres| AEME) \end{matrix}$ 的值由系统周围电磁环境和耦合途径确定。若P $\begin{matrix} (Stres| AEME) \end{matrix}$ =0, 则表明对器件无影响。如果知道器件的电磁敏感度概率密度函数f $\begin{matrix} (x) \end{matrix}$ , 则P $\begin{matrix} (Stres| AEME) \end{matrix}$ 与f $\begin{matrix} (x) \end{matrix}$ 和g $\begin{matrix} (y) \end{matrix}$ 重叠部分成比例, 即:

P $\begin{matrix} (Stres| AEME) \end{matrix}$ ∝

$\begin{matrix} \int_{x_{\min}}^{y_{\max}} \end{matrix}$ g_k $\begin{matrix} (y) \end{matrix}$ dy, y∈ $\begin{matrix} [x_{\min}, y_{\max}] \end{matrix}$ (9)

3.3 P $\begin{matrix} (Comp, Stres) \end{matrix}$ 计算

电磁应力概率密度函数g $\begin{matrix} (y) \end{matrix}$ 和器件敏感度概率密度函数f $\begin{matrix} (x) \end{matrix}$ 确定的情况下, 如图6所示, P $\begin{matrix} (Comp, Stres) \end{matrix}$ 的表达式为^[10]:

P $\begin{matrix} (Comp, Stres) \end{matrix}$ = $\begin{matrix} \int_{x_{\min}}^{y_{\max}} \end{matrix}$ g $\begin{matrix} (y) \end{matrix}$ dy $\begin{matrix} \int_{x_{\min}}^{y} \end{matrix}$ f $\begin{matrix} (x) \end{matrix}$ dx(10)

	Figure Option View Download New Window
	图6 BN中器件失效概率Fig.6 Failure probability of component in BN

3.4 P $\begin{matrix} (Subs |Comp) \end{matrix}$ 和P $\begin{matrix} (V |Subs) \end{matrix}$ 计算

P $\begin{matrix} (Subs |Comp) \end{matrix}$ 和P $\begin{matrix} (V |Subs) \end{matrix}$ 的获得可以借鉴P $\begin{matrix} (AEME| IEMI) \end{matrix}$ 的分析过程。

4 验证分析

以HEMP为例对电子节气门敏感度BN评估模型计算进行详细说明。对BN中的每个节点和分支进行分析, 尤其是各电子器件经受电磁应力和敏感度情况的分析。

4.1 辐射电磁应力计算和敏感度分析

只考虑HEMP 作为干扰源, 假设HEMP 传播到车辆周围时波形不发生变化。可得:

P(HEMP)=P(V₀)=1(11)

P(AEME, HEMP)=P(V₁, V₀)=P( $\begin{matrix} V_{1}| \end{matrix}$ V₀)P(V₀)=1 (12)

由于车辆壳体是金属结构, 对HEMP有一定的屏蔽作用, 发动机舱各位置处场强峰值均值约为33 kV/m^[15]。节气门体和ECU均为金属外壳, 可简单等效为留有孔洞的屏蔽腔体, 在不考虑谐振频率的情况下, 屏蔽效能可达80 dB^[16]。考虑孔缝大小等因素, 设备壳体屏蔽效能设为40 dB。经上述粗略计算, 设备壳体内场强小于500 V/m。而微控系统的辐射敏感度阈值大于1 kV/m^[17]。因此, 认为节气门控制系统受辐射干扰故障的概率为0, 即:

P( $\begin{matrix} Comp| \end{matrix}$ Stres)=P(Comp< Stres)=0(13)

4.2 传导电磁应力计算和敏感度分析

传导电磁应力由线缆拾取发动机舱内电磁能量产生的, HEMP经过车辆壳体后波形会发生变化, 详细计算发动机舱内电磁环境复杂且费时。为了降低数据获取的难度, 仍然用双指数波形来描述发动机舱内电磁环境, 峰值场强取为33 kV/m 。假设发动机舱内连接ECU和节气门的所有线缆相同且独立, 可认为线缆端器件经受相同传导电磁应力。电磁敏感度阈值为器件能承受的最大EMS。

4.2.1 传导电磁应力计算

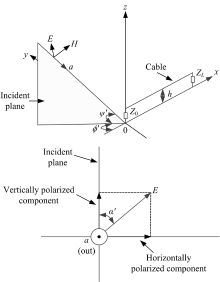
用CST线缆工作室(Cable studio)仿真计算电磁脉冲辐射下单根导线终端感应电压V(L), 取电压峰值作为器件经受的EMS值, 仿真模型示意图如图7所示。

	Figure Option View Download New Window
	图7 入射平面波对导线的激励Fig.7 Cable excited by incident plane wave

图7中入射波为平面波, 将其参数作为随机变量, 兼顾计算量和样本数量, 具体设为:入射角ψ '∈ [18° , 90° ], 方位角ϕ '∈ [0, 90° ], 极化角α '∈ [0, 90° ]作为随机变量, 各变量采样步长都设为Δ =18° , 共计180个仿真样本。

其他仿真参数为:①激励源EMP:激励源数学模型E(t)=kE₀(e^-α^t-e^-β^t), E₀=33 kV/m, k=1.3, α =4× 10⁷, β =6× 10⁸; ②线缆:长度L=2 m, 高度h=0.6 m, 导线导体半径r=0.5 mm, 终端负载Z₀=3 Ω , Z_L=10 kΩ , Z₀为节气门端阻抗, Z_L为ECU端输入阻抗; ③参考地:导电率σ _g=0.01 S/m, 介电常数ε _rg=10。

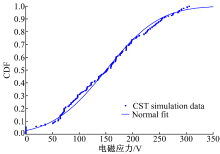
180个样本结果中, Z₀端EMS最大为305.6 V, 最小为0 V。假设Z₀端EMS符合正态分布, 用K-S检验(Kolmogorov-Smirnov test)进行验证。通过查表获得α ^*=0.05时, 临界值CV为0.10122^[10]。CST仿真获得线缆终端EMS结果累积分布函数(Cumulative distribution function, CDF)与均值μ =150.045、标准差σ =78.384的正态分布CDF最大偏差为0.0563, 小于CV, 如图8所示。

	Figure Option View Download New Window
	图8 电子节气门端电磁应力累积分布函数Fig.8 CDF of EMS atelectronic throttle terminal

因此, 认为线缆终端EMS符合μ =150.045V, 标准差σ =78.384V的正态分布N(μ , σ ²), 概率密度函数(Probability density function, PDF)如式(14)所示:

f(x)= $\begin{matrix} \frac{1}{σ \sqrt[]{2 π}} \end{matrix}$ exp $\begin{matrix} (- \frac{1}{2} {(\frac{x - μ}{σ})}^{2}) \end{matrix}$ (14)

4.2.2 器件传导敏感度测试

节气门电机和TPS敏感度测试采用IEC 61000-4-4^[18]中规定的电子设备电快速瞬变脉冲(Electrical fast transients, EFT)敏感度测试方法, 试验布置如图9所示。控制节气门阀以2 Hz的频率开合, 分别对电机控制线和TPS信号线注入干扰脉冲, 通过观察节气门开合情况和TPS信号波形判断节气门电机和TPS故障模式。注入脉冲幅值由小到大增加, 直到受试器件功能异常或达到设备输出最大值。整个试验过程记录受试器件故障模式和耦合干扰脉冲峰值。对20个样本进行试验, 相同故障类型数据进行正态分布拟合, 获得节气门电机和TPS敏感度阈值的累积分布函数和概率密度函数。

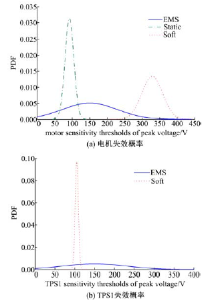
	Figure Option View Download New Window
	图9 电子节气门敏感度试验布置Fig.9 Electronic throttle under test

节气门电机在试验过程中出现了静态干扰(Static)和软损伤(Soft)两种故障模式。静态干扰指电机运行过程中出现卡顿现象, 但不影响节气门开合; 软损伤指干扰脉冲造成电机停止工作, 复位后功能恢复正常。节气门位置传感器只出现了软损伤一种故障模式, 即干扰脉冲使传感器信号消失。节气门电机和TPS各故障模式对应敏感度阈值如图10所示, 敏感度阈值概率密度函数见表1、表2。

	Figure Option View Download New Window
	图10 电子节气门敏感度阈值Fig.10 Sensitivity thresholds of electronic throttle

4.2.3 传导故障概率计算

电机和TPS每一种故障模式失效概率可通过下式获得:

P_c=P(Comp, Stres)=P(y≥ x)

= $\begin{matrix} \int_{x_{\min}}^{y_{\max}} \end{matrix}$ g $\begin{matrix} (y) \end{matrix}$ dy $\begin{matrix} \int_{x_{\min}}^{y} \end{matrix}$ f $\begin{matrix} (x) \end{matrix}$ dx (15)

式中:Comp代表节点C_1.1.1, C_1.1.2, C_1.2; Stres代表V_{2, 1, 1}, V_{2, 1, 2}和V_{2, 1, 3}; f $\begin{matrix} (x) \end{matrix}$ 和g $\begin{matrix} (y) \end{matrix}$ 分别代表器件敏感度阈值PDF和电磁应力PDF; x∈ $\begin{matrix} [x_{\min}, x_{\max}] \end{matrix}$ 和y∈ $\begin{matrix} [y_{\min}, y_{\max}] \end{matrix}$ 分别是敏感度阈值电压范围和电磁应力电压范围。若X~N(μ , σ ²), F(μ -3σ ≤ x≤ μ +3σ )≈ 99.7%。可将[μ -3σ , μ +3σ ]作为x_min、x_max、y_min、y_max的取值。电子节气门各器件敏感度阈值PDF和电磁应力PDF如图11所示, 失效概率P_c见表1、表2。

电磁应力PDF和敏感度阈值PDF重叠部分反映了对应耦合途径的威胁程度, 用P_t表示。

P $\begin{matrix} (Stres |AEME) \end{matrix}$ =P_t= $\begin{matrix} \int_{x_{\min}}^{y_{\max}} \end{matrix}$ g $\begin{matrix} (y) \end{matrix}$ dy(16)

耦合路径L₁、L₂最大P_t如表1、表2所示, 分别为:

TPS1:P $\begin{matrix} (V_{2, 1, 1} |V_{1}) \end{matrix}$ ≈ 0.74(17)

节气门电机:P $\begin{matrix} (V_{2, 1, 3} |V_{1}) \end{matrix}$ ≈ 0.86(18)

表1 电机敏感度阈值分布 Table 1 Sensitivity thresholds distribution of motor

表2 TPS1敏感度阈值分布 Table2 Sensitivity thresholds distribution of TPS1

	Figure Option View Download New Window
	图11 电子节气门器件失效概率Fig.11 Failure probability of electronic throttle components

4.2.4 电子节气门敏感度评估

需要说明的是, 本文只研究节气门的敏感度情况, 对电控单元的敏感度情况不做探讨。经过辐射和传导敏感度分析, 所有安全的节点和路径被删除, 多故障模式器件节点将被展开。将节气门电机节点C_1.2展开成C_1.2.1和C_1.2.2。由于节气门位置传感器C_1.1.1和C_1.1.2完全一样, 耦合路径也相同, 因此, 用V_2.1.1代替V_2.1.2。

图3中模型经简化后如图12所示。导致节气门故障的情况有两个, 一是HEMP(V₀)穿过发动机舱体(V₁)耦合到线缆L₁造成TPS1(C_1.1.1)和TPS2(C_1.1.2)受扰, 导致TPS(C_1.1)工作失效; 另一个是线缆L₂引入干扰造成节气门电机(C_1.2)工作失效。各效应之间相互独立, 式(2)可表示为:

P_V $\begin{matrix} (V, IEMI) \end{matrix}$ =P $\begin{matrix} (V_{2, 1, 1}, V_{0}) \end{matrix}$ × P $\begin{matrix} (C_{1.1}, V_{2, 1, 1}) \end{matrix}$ P $\begin{matrix} (C_{1} |C_{1.1}) \end{matrix}$ P $\begin{matrix} (V |C_{1}) \end{matrix}$ +P $\begin{matrix} (V_{2, 1, 3}, V_{0}) \end{matrix}$ P $\begin{matrix} (C_{1.2}, V_{2, 1, 3}) \end{matrix}$ P $\begin{matrix} (C_{1} |C_{1.2}) \end{matrix}$ × P $\begin{matrix} (V |C_{1}) \end{matrix}$ (19)

式中:P $\begin{matrix} (V_{2, 1, i}, V_{0}) \end{matrix}$ =P $\begin{matrix} (V_{0}) \end{matrix}$ P $\begin{matrix} (V_{1} |V_{0}) \end{matrix}$ ×

P $\begin{matrix} (V_{2, 1, i} |V_{1}) \end{matrix}$ , i=1, 3。

	Figure Option View Download New Window
	图12 简化后BN模型Fig.12 Modified BN model

C_1.1.1和C_1.1.2采用冗余设计, 两者同时故障将导致C_1.1失效。所以, 条件概率为:

P $\begin{matrix} (C_{1.1} |C_{1.1 . 1}, C_{1.1 . 2}) \end{matrix}$ =1(20)

联合概率为:

P $\begin{matrix} (C_{1.1}, C_{1.1 . 1}, C_{1.1 . 2}) \end{matrix}$ =

P $\begin{matrix} (C_{1.1 . 1}) \end{matrix}$ P $\begin{matrix} (C_{1.1 . 2}) \end{matrix}$ P $\begin{matrix} (C_{1.1} |C_{1.1 . 1}, C_{1.1 . 2}) \end{matrix}$ (21)

式中:P $\begin{matrix} (C_{1.1 . 1}) \end{matrix}$ =P $\begin{matrix} (C_{1.1 . 2}) \end{matrix}$ =P $\begin{matrix} (C_{1.1 . 1}, V_{2, 1, 1}) \end{matrix}$ , 因此:

P $\begin{matrix} (C_{1.1}) \end{matrix}$ =

P $\begin{matrix} (C_{1.1 . 1}, V_{2.1 . 1}) \end{matrix}$ P $\begin{matrix} (C_{1.1 . 2}, V_{2.1 . 1}) \end{matrix}$ × 1=

0.6927× 0.6927≈ 0.4798 (22)

节气门电机包括静态干扰和软损伤两种故障模式, 可用各故障模式概率加权和表示电机故障概率。权值P_w表示各故障模式出现的概率, 可由专家经验给出, 这里P_w=P $\begin{matrix} (C_{1.1 .i} |V_{2, 1, 3}) \end{matrix}$ , i=1, 2, w=1, 2, 分别赋值为2/3和1/3。用全概率公式求节气门电机的联合概率如下式所示:

P $\begin{matrix} (C_{1.2}, V_{2, 1, 3}) \end{matrix}$ = $\begin{matrix} \overset{2}{\sum_{k = 1}} \end{matrix}$ P $\begin{matrix} (C_{1.2} |C_{1.2 .k}) \end{matrix}$ P $\begin{matrix} (C_{1.2 .k}, V_{2, 1, 3}) \end{matrix}$ =0.7434× $\begin{matrix} \frac{2}{3} \end{matrix}$ +0.0037× $\begin{matrix} \frac{1}{3} \end{matrix}$ ≈ 0.4968(23)

位置传感器C_1.1和电机C_1.2构成了电子节气门C₁所有失效情况集合, 从执行器角度考虑, 电机比位置传感器更加重要。因此, 条件概率分配为:

P $\begin{matrix} (C_{1} |C_{1.1}) \end{matrix}$ = $\begin{matrix} \frac{1}{3} \end{matrix}$ , P $\begin{matrix} (C_{1} |C_{1.2}) \end{matrix}$ = $\begin{matrix} \frac{2}{3} \end{matrix}$ (24)

C₁直接导致V故障, 因此:

P $\begin{matrix} (V |C_{1}) \end{matrix}$ =1(25)

基于以上分析, 有:

P $\begin{matrix} (V |V_{2, 1, 1}) \end{matrix}$ =P $\begin{matrix} (C_{1.1}, V_{2, 1, 1}) \end{matrix}$ P $\begin{matrix} (C_{1} |C_{1.1}) \end{matrix}$ P $\begin{matrix} (V |C_{1}) \end{matrix}$ =0.4798× $\begin{matrix} \frac{1}{3} \end{matrix}$ × 1≈ 0.1599(26)P $\begin{matrix} (V |V_{2, 1, 3}) \end{matrix}$ =P $\begin{matrix} (C_{1.2}, V_{2, 1, 3}) \end{matrix}$ P $\begin{matrix} (C_{1} |C_{1.2}) \end{matrix}$ P $\begin{matrix} (V |C_{1}) \end{matrix}$ =0.4968× $\begin{matrix} \frac{2}{3} \end{matrix}$ × 1≈ 0.3312(27)

最后, 电子节气门故障概率为:

P $\begin{matrix} (V, IEMI) \end{matrix}$ =P $\begin{matrix} (V_{2, 1, 1}, V_{0}) \end{matrix}$ P $\begin{matrix} (V |V_{2, 1, 1}) \end{matrix}$ +P $\begin{matrix} (V_{2, 1, 3}, V_{0}) \end{matrix}$ P $\begin{matrix} (V |V_{2, 1, 3}) \end{matrix}$ =0.74× 0.1599+0.86× 0.3312≈ 0.4032(28)

这表明电子节气门在HEMP辐射下故障概率为40.32%。

5 结束语

本文研究了电子节气门在IEMI下的敏感度评估问题, 结合电磁拓扑理论和故障树分析方法建立了BN评估模型, 给出了模型各节点概率的计算方法。最后以HEMP环境为例说明了模型分析、计算的全过程, 结果表明电子节气门在HEMP环境下的故障概率为40.32%。本文所采用的基于BN的评估方法融合了电磁环境分析、耦合路径分析、元器件敏感度测试和数据统计处理等过程, 涵盖从干扰源到电子节气门故障整个作用过程的分析。解决了通过辐射试验方法无法观察所有不确定参量下节气门效应引起的试验结果外推性差、评估不准确和试验成本昂贵的难题。同时, 确定了主要干扰耦合通道和节气门敏感器件, 对发动机敏感度评估和电磁防护设计具有重要参考价值。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李慧梅, 唐彦峰, 刘祥凯, 等. 电磁脉冲武器对车辆装备的损伤效应研究[J]. 装备环境工程, 2010, 7(3): 31-34. Li Hui-mei, Tang Yan-feng, Liu Xiang-kai, et al. Study of destructive effects of electromagnetic pulse weapon on vehicle[J]. Equipment Environment Engineering, 2010, 7(3): 31-34. [本文引用:3]
[2]	Nitsch D, Camp M, Sabath F, et al. Susceptibility of some electronic equipment to HPEM threats[J]. IEEE Transactions on Electromagnetic Compatibility, 2004, 46(3): 380-389. [本文引用:1]
[3]	Bäckström M G, Lövstrand K G. Susceptibility of electronic systems to high-power microwaves: summary of test experience[J]. IEEE Transactions on Electromagnetic Compatibility, 2004, 46(3): 396-403. [本文引用:1]
[4]	曾德龙. 汽车电子设备电磁损伤机理及损伤阈值研究[D]. 长春: 吉林大学通信工程学院, 2012. Zeng De-long. Research on electromagnetic damage mechanisms and threshold values of electricalequipments on vehicle [D]. Changchun: College of Communication and Engineering, Jilin University, 2012. [本文引用:1]
[5]	孟凡宝. 高功率超宽带电磁脉冲技术[M]. 北京: 国防工业出版社, 2011. [本文引用:1]
[6]	Mensing R W, King R J, Cabayan H S. A method for estimating the susceptibility of electronic systems to HPM (high power microwave)[R]. NASA STI/RECON Techinical Report, 1988. [本文引用:1]
[7]	梁喆. 基于故障树分析车载系统电磁兼容诊断方法研究[D]. 西安: 西安电子科技大学机电工程学院, 2012. Liang Zhe. Research on automotive system electromagnetic compatibility diagnosis based on fault tree analysis method[D]. Xi̓an: School of Mechanic-Electronic Engineering Xidian University, 2012. [本文引用:1]
[8]	Genender E, Garbe H, Sabath F. Probabilistic risk analysis technique of intentional electromagnetic interference at system level[J]. IEEE Transactions on Electromagnetic Compatibility, 2014, 56(1): 200-207. [本文引用:1]
[9]	刘钰, 韩峰, 陆希成, 等. 电子系统电磁脉冲易损性评估的分层贝叶斯网络模型[J]. 电子学报, 2016, 44(11): 2695-2703. Liu Yu, Han Feng, Lu Xi-cheng, et al. EMP susceptibility modeling and assessment of electronic system based on hierarchical Bayesian networks[J]. Acta Electronica Sinica, 2016, 44(11): 2695-2703 [本文引用:2]
[10]	Mao C, Canavero F. System-level vulnerability assessment for EME: from fault tree analysis to Bayesian networks-part I: methodology framework[J]. IEEE Transactions on Electromagnetic Compatibility, 2016, 58(1): 180-187. [本文引用:5]
[11]	IEC TR 61000-1-5, 2004. Electromagnetic compatibility (EMC)-part 1-5: general-high power electromagnetic (HPEM) effects on civil systems[S]. [本文引用:1]
[12]	王建国, 刘国治, 周金山. 微波孔缝线性耦合函数研究[J]. 强激光与粒子束, 2003, 15(11): 1093-1099. Wang Jian-guo, Liu Guo-zhi, Zhou Jin-shan. Investigations on function for linear coupling of microwaves into slots[J]. High Power Laser and Particle Beams, 2003, 15(11): 1093-1099. [本文引用:1]
[13]	王建国. 高空核爆炸效应参数手册[M]. 北京: 原子能出版社, 2010. [本文引用:1]
[14]	Lovetri J, Costache G I. An electromagnetic interaction modeling advisor[J]. IEEE Transactions on Electromagnetic Compatibility, 1991, 33(3): 241-251. [本文引用:1]
[15]	蔡金良, 孙晓颖, 赵晓晖. 考虑复杂金属设备的车辆发动机舱电磁环境效应分析[J]. 吉林大学学报: 工学版, 2016, 46(4): 1360-1367. Cai Jin-liang, Sun Xiao-ying, Zhao Xiao-hui. Electromagnetic environment effects for automotive engine block with complex metallic equipments[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(4): 1360-1367. [本文引用:1]
[16]	王迪. HEMP环境下车辆电磁屏蔽技术的防护效能研究[D]. 长春: 吉林大学通信工程学院, 2015. Wang Di. Research on protection effectiveness of vehicle electromagnetic shielding techniques in HEMP environment[D]. Changchun: College of Communication and Engineering, Jilin University, 2015. [本文引用:1]
[17]	Camp M, Gerth H, Garbe H, et al. Predicting the breakdown behavior of microcontrollers under EMP/UWB impact using a statistical analysis[J]. IEEE Transactions on Electromagnetic Compatibility, 2004, 46(3): 368-379. [本文引用:1]
[18]	IEC 61000-4-4, 2012. EMC: Testing and measurement techniques-electrical fast transient/burst immunity test[S]. [本文引用:1]

2010

0.0

. 2010, 7(3):31-34

Study of destructive effects of electromagnetic pulse weapon on vehicle

电磁脉冲武器对车辆装备的损伤效应研究

Li Hui-mei , Tang Yan-feng , Liu Xiang-kai

李慧梅, 唐彦峰, 刘祥凯

... 0 引言电磁脉冲(Electromagnetic pulse,EMP)等有意电磁干扰(Intentional electromagnetic interference,IEMI)严重威胁了车辆机动性和行驶安全性^[1] ...

... 目前电磁脉冲效应的研究,主要采用试验方法获得电子系统的效应类型和敏感度阈值^[1,2,3,4] ...

... 电磁脉冲对车辆装备的损伤效应主要分为工作失灵和功能损坏^[1] ...

2004

0.0

... 目前电磁脉冲效应的研究,主要采用试验方法获得电子系统的效应类型和敏感度阈值^[1,2,3,4] ...

2004

0.0

... 目前电磁脉冲效应的研究,主要采用试验方法获得电子系统的效应类型和敏感度阈值^[1,2,3,4] ...

2012

0.0

. 2012, :-

Research on electromagnetic damage mechanisms and threshold values of electricalequipments on vehicle

汽车电子设备电磁损伤机理及损伤阈值研究[D]

Zeng De-long

曾德龙

随着汽车电子化、自动化程度的不断提升以及所处电磁环境的日趋复杂，由电磁脉冲（EMP）引起的电磁损伤问题已成为影响汽车安全性的重要隐患之一。电磁脉冲能够引起电子设备状态反转、功放器件性能下降、执行器误动作等暂时的性能降低，严重时可引起半导体器件、继电器等敏感设备永久性损伤，导致汽车无法正常工作。深入研究汽车电子设备的电磁脉冲损伤机理，确定引起设备损伤的电磁脉冲强度及分布规律，可为汽车电磁防护提供理论依据及数据支撑。为阐明电磁脉冲作用于汽车电子设备时的损伤机理并确定损伤阈值，本文以某型轿车为对象，对汽车线束内平行导线间传导耦合规律进行了较深入的研究，设计并搭建了电磁脉冲损伤阈值测试平台，对晶体三极管、场效应管等典型电子元器件及电控分系统的电磁脉冲损伤阈值进行了测试，并对损伤阈值分布规律进行了分析，给出了汽车电子设备电磁脉冲损伤阈值的系统化测试方法。针对汽车线束内传导耦合问题，以ISO7637-3中电子设备传导耦合敏感度测试方法为基础，在0-200MHz频率范围内的76个频点分别进行了单频点耦合效率测试。通过对平行导线间距0cm和1cm时耦合效率的测试、导线间线束对耦合效率影响的分析以及距地面高度为2cm、5cm和10cm时耦合效率的比较，分析了线束内传导耦合的基本规律。针对汽车敏感设备中的典型半导体电磁脉冲损伤阈值问题，依照GJB538-88中半导体器件测试方法，使用脉冲群发生器做为干扰源、示波器做为测量设备，设计并搭建了测试平台。通过对S9018型晶体三极管、IRF540N增强型N沟道CMOS管及HD74LS04型TTL器件进行损伤阈值测试，获得近150组损伤阈值测试数据。通过数据分析，得到损伤阈值变化范围、与电磁脉冲功率及能量关系和其分布规律，为相关敏感设备器件选择及防护强度提供依据。针对汽车分系统电磁脉冲损伤阈值问题，根据ISO11451等相关试验标准设计并搭建分系统损伤阈值测试平台，得到了某型轿车电子节气门、转速传感器、进气温度及压力传感器等电子设备实测损伤阈值。给出了试验台布置、试验标定、测试方法等，为汽车电子设备电磁损伤测试提供系统化测试方法。主要贡献如下： a.初步定义了汽车电控设备受干扰及损伤阈值等级，为电控设备干扰及损伤阈值界定提供依据。通过实测得到晶体三极管、场效应管等典型半导体元器件及电控分系统损伤阈值，给出了损伤阈值分布规律、电磁脉冲功率、能量与损伤阈值的关系，为汽车电磁防护提供了数据基础。 b.设计并搭建了半导体阈值测试平台、分系统干扰及损伤阈值测试平台，通过对典型器件及系统的测试，验证了测试平台和测试方法的正确性及可行性。 c.以搭建的损伤测试平台和实测数据为基础，汽车干扰及损伤测试标准为依据，从试验设置方法、标定方法及干扰能量加载方法等方面，探索并得到了汽车电子设备电磁脉冲干扰及损伤阈值的系统化测试方法。上述工作为电子设备电磁敏感度研究提供部分数据基础，为汽车电子设备损伤阈值测试提供了借鉴方法，对汽车电子设备电磁损伤及防护技术研究具有一定的参考价值。

... 目前电磁脉冲效应的研究,主要采用试验方法获得电子系统的效应类型和敏感度阈值^[1,2,3,4] ...

2011

0.0

... 由于试验条件和成本的限制,试验样本有限,试验结论不具备很强的外推性^[5] ...

1988

0.0

... 具有代表性的不确定性评估方法主要有故障树分析(Fault tree analysis,FTA)方法^[6,7,8]和贝叶斯网络(Bayesian networks,BN)分析方法^[9,10] ...

2012

0.0

. 2012, :- DOI:doi:10.7666/d.y2068055

Research on automotive system electromagnetic compatibility diagnosis based on fault tree analysis method

基于故障树分析车载系统电磁兼容诊断方法研究[D]

Liang Zhe

梁喆

车载系统作为一个复杂的电子系统，其电磁兼容问题异常突出，因而针对车载系统电磁兼容问题的故障诊断显得尤为重要。由于整体系统结构复杂、影响因素较多、各个子系统之间关系密集，所以，对于较复杂问题的故障诊断需要结合一些特定的故障诊断方法才能满足实际的使用要求。　　本文以车载系统电磁兼容问题为研究目标，依据建立故障树的原则，确定系统上装电台故障受扰为顶事件，再根据电磁兼容三要素分析方法将车载系统内部传导干扰和辐射干扰进行逐一细分，分别找出此故障树的中间事件和底事件，并由逻辑关系建立电磁干扰故障树；接着运用布尔算法求出...

... 具有代表性的不确定性评估方法主要有故障树分析(Fault tree analysis,FTA)方法^[6,7,8]和贝叶斯网络(Bayesian networks,BN)分析方法^[9,10] ...

2014

0.0

... 具有代表性的不确定性评估方法主要有故障树分析(Fault tree analysis,FTA)方法^[6,7,8]和贝叶斯网络(Bayesian networks,BN)分析方法^[9,10] ...

2016

0.0

. 2016, 44(11):2695-2703 DOI:doi:10.3969/j.issn.0372-2112.2016.11.019

EMP susceptibility modeling and assessment of electronic system based on hierarchical Bayesian networks

电子系统电磁脉冲易损性评估的分层贝叶斯网络模型

Liu Yu , Han Feng , Lu Xi-cheng

刘钰, 韩峰, 陆希成

A modeling method based on hierarchical Bayesian networks (HBN) which can be used in the susceptibility assessment of electronic system interfered by electromagnetic pulse (EMP) is proposed.According to the hierarchical structure of the electronic system and the feature of its EMP effects,steps to assess the system susceptibility are discussed.Analyzing the couple path by using the interaction sequence diagram (ISD),and the proper volume nodes of the base level of the ISD and the probability distribution of the electromagnetic stress in these nodes are determined.The topology relationship between the HBN and ISD is created by adding the directed arc from the base proper volume nodes of the ISD to the root nodes of HBN.The base proper volume level is considered as new root level to rebuild the HBN of system which can be used as the susceptibility assessment model of electronic system interfered by EMP.A case study demonstrates the effectiveness of the proposed methodology.

针对电子系统电磁脉冲易损性评估问题，提出了基于分层贝叶斯网络的电子系统电磁脉冲易损性评估模型建模方法.分析了电子系统分层结构特征及其电磁脉冲效应的特点，应用电磁拓扑理论中的相互作用顺序图分析系统电磁耦合途径，确定系统内底层屏蔽区域节点，研究了相互作用顺序图与系统分层贝叶斯网络的拓扑关联关系，在系统分层贝叶斯网络模型中增加底层屏蔽区域节点层，从而建立系统易损性评估模型，并给出了相应的建模步骤.最后以某电子机械传动系统电磁脉冲易损性评估问题为例说明了建模和计算过程.

... 具有代表性的不确定性评估方法主要有故障树分析(Fault tree analysis,FTA)方法^[6,7,8]和贝叶斯网络(Bayesian networks,BN)分析方法^[9,10] ...

... FTA方法广泛应用于系统可靠性和安全性分析,但在评估系统电磁敏感度时存在以下不足:①对于一些复杂系统,导致顶事件的基本事件较多,造成基于最小割集布尔运算的计算十分复杂^[9] ...

2016

0.0

... 具有代表性的不确定性评估方法主要有故障树分析(Fault tree analysis,FTA)方法^[6,7,8]和贝叶斯网络(Bayesian networks,BN)分析方法^[9,10] ...

... ②故障树(Fault tree,FT)模型中不包含导致故障发生的电磁环境和电磁应力分析^[10],无法完整描述电磁波与系统相互作用的全过程 ...

... 文献[10]中提出了电子系统电磁易损性评估的贝叶斯网络框架,将FT和电磁拓扑(Electro-magnetic topology,EMT)等工具有效融合在BN中,为电子系统电磁易损性评估提供了更加有力的分析工具 ...

... 电磁应力概率密度函数gy和器件敏感度概率密度函数fx确定的情况下,如图6所示,PComp,Stres的表达式为^[10]: ...

... 10122^[10] ...

2004

0.0

... ③系统电磁效应有功能正常、逻辑紊乱和硬件损伤3种状态^[11],而故障树分析中只包含两种逻辑状态,对于多故障状态需要特殊对待 ...

2003

0.0

. 2003, 15(11):1093-1099

Investigations on function for linear coupling of microwaves into slots

微波孔缝线性耦合函数研究

Wang Jian-guo , Liu Guo-zhi , Zhou Jin-shan

王建国, 刘国治, 周金山

... 孔缝附近电磁波产生增强效应,使耦合场强于入射场^[12] ...

2010

0.0

... 这些线缆拾取发动机舱V₁内电磁能量,以瞬态高电压和大电流的形式传导到终端负载,对节气门电子器件产生传导干扰^[13] ...

1991

0.0

... 参照文献[14]中EMT表示方法,将发动机舱外部和内部分别用V₀和V₁表示,节气门体和电控单元壳体分别用V_2,1和V_2,2表示 ...

2016

0.0

. 2016, 46(4):1360-1367 DOI:doi:10.13229/j.cnki.jdxbgxb201604049

Electromagnetic environment effects for automotive engine block with complex metallic equipments

考虑复杂金属设备的车辆发动机舱电磁环境效应分析

Cai Jin-liang , Sun Xiao-ying , Zhao Xiao-hui

蔡金良, 孙晓颖, 赵晓晖

To precisely analyze the electromagnetic environment in automotive engine block radiated by High Electromagnetic Pulse (HEMP), the complex metallic equipments with different shapes at different positions, such as radiator, engine and gear-box were considered. The electric fields were computed at more than 500 points in the block, and the results were verified using self-reference method. Finally, the electromagnetic environment was analyzed from views of the electric field distribution, the frequency of occurrence of peak value and the electric field resonances. The results show that the electric peak values are Rayleigh distributed. The radiator leads the shift of the resonance frequency, and the engine results in the increase in electric field in important region. Metallic equipments evidently impact on the maximum electric field peak values in the block, which is doubled.

... 由于车辆壳体是金属结构,对HEMP有一定的屏蔽作用,发动机舱各位置处场强峰值均值约为33 kV/m^[15] ...

2015

0.0

. 2015, :-

Research on protection effectiveness of vehicle electromagnetic shielding techniques in HEMP environment

HEMP环境下车辆电磁屏蔽技术的防护效能研究

Wang Di

王迪

HEMP（高空核爆电磁脉冲）具有超强的电磁能量，能够干扰甚至毁坏覆盖范围内的电子系统。随着车辆电子信息化程度的不断提高，车辆内部集成的电子系统越来越多，极易受到HEMP的干扰，影响车辆的机动性与安全性。车窗、设备孔缝和线缆是车辆电子设备引入外部电磁干扰的主要途径，也是电磁脉冲防护设计需要考虑的主要环节。研究HEMP环境下车窗、设备孔缝和线缆的屏蔽技术及其防护效能，是进行车辆HEMP防护设计与工程实施的前提和基础，具有重要的理论与应用价值。针对车窗屏蔽主要研究金属网屏蔽技术，利用传输线法计算单孔和均匀孔阵金属腔体的屏蔽效能，确定网孔形状以及丝径、网孔尺寸对屏蔽效能的影响；利用非均匀金属网代替均匀金属网，使车窗屏蔽做到既不影响驾驶员视线又具有较好的屏蔽效能，并通过试验与CST仿真验证非均匀金属网的有效性；建立两种金属网屏蔽某型车车窗的CST模型，由于本文研究的金属网屏蔽技术主要应用于车窗屏蔽，主要用于抑制驾驶舱内部的电磁干扰，因此简化整车仿真模型，只取驾驶舱为建模对象，仿真分析在HEMP环境下，某型车驾驶室内部的仪表盘、收音机、车内中心、驾驶员位置处的电场强度及屏蔽效能，验证了非均匀金属网的屏蔽效果。针对电子设备屏蔽主要研究设备壳体散热孔屏蔽问题，采用外加金属腔和金属波导两种方式，理论计算外加腔体长度以及波导厚度、尺寸、长度对屏蔽效能的影响；建立电子设备外加金属腔以及外加波导的CST仿真模型，对比分析它们的屏蔽效能，确定波导具有较好的屏蔽效能；设计波导结构，建立金属波导屏蔽车壳前方散热孔的仿真模型，由于本文将波导屏蔽技术应用于车壳前方的散热孔，主要用于抑制发动机舱内部的电磁干扰，因此简化整车仿真模型，只取发动机舱为CST建模对象，分析发动机舱内部的发动机、ECU、散热器位置处的屏蔽效能。针对线缆屏蔽主要研究部分裸露屏蔽线问题，通过试验与CST仿真方法研究HEMP环境下裸露长度对屏蔽线电磁干扰的影响，在CST仿真建模方面，将理论计算的屏蔽层转移阻抗导入到仿真模型中，得到屏蔽层特性；仿真分析HEMP环境下裸露端屏蔽层接地、屏蔽线总长度、芯线半径对裸露端干扰电压的影响；建立某型车发动机舱仿真模型，并分析车上节气门传感器线缆防护前后的干扰电压；计算屏蔽线的特性阻抗，分析不同负载阻抗（包括特性阻抗）时线缆末端的干扰电压与屏蔽效能。论文主要贡献包括：（1）利用非均匀金属网代替均匀金属网屏蔽车窗，在驾驶员正前方、倒车镜附近等影响驾驶员视线的位置安装较大网孔金属网，其它不影响驾驶员视线的车窗位置安装较小网孔金属网；简化某型车壳体结构并建立仿真分析模型，仿真数据表明非均匀金属网在兼顾了对驾驶员视线影响的同时又具有较好的屏蔽效能。（2）设计了某型车壳体前方散热孔的屏蔽波导结构，简化某型车壳体结构并建立发动机舱仿真分析模型，仿真分析HEMP环境下发动机舱内部的发动机、ECU、散热器位置处的屏蔽效能。（3）分析屏蔽层裸露长度、屏蔽层裸露端接地等因素对干扰电压的影响；以实际尺寸的节气门位置传感器线缆为研究对象，结合某型车实际结构，仿真分析不同负载阻抗下线缆引入的干扰电压与屏蔽效能。结论表明为提高线缆的防护能力，要尽量避免屏蔽线的裸露，若无法避免也要尽量做到屏蔽层两端接地；在保证全屏蔽的要求下，可以通过设计屏蔽层参数，进一步降低电磁干扰。上述工作对车辆电磁屏蔽技术的防护效能进行了研究，为屏蔽技术的选择、设计与实施提供了参考方案，具有很好的实用价值。

... 节气门体和ECU均为金属外壳,可简单等效为留有孔洞的屏蔽腔体,在不考虑谐振频率的情况下,屏蔽效能可达80 dB^[16] ...

2004

0.0

... 而微控系统的辐射敏感度阈值大于1 kV/m^[17] ...

2012

0.0

... 节气门电机和TPS敏感度测试采用IEC 61000-4-4^[18]中规定的电子设备电快速瞬变脉冲(Electrical fast transients,EFT)敏感度测试方法,试验布置如图9所示 ...