蜂窝式立体元图像阵列的生成

引用本文

武伟, 王世刚, 赵岩, 韦健, 钟诚. 蜂窝式立体元图像阵列的生成[J].吉林大学学报（工学版）, 2018,48(1): 290-294
WU Wei, WANG Shi-gang, ZHAO Yan, WEI Jian, ZHONG Cheng. Hexagonal elemental image array generation[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 290-294 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170227
Permissions

蜂窝式立体元图像阵列的生成

武伟^1,², 王世刚¹, 赵岩¹, 韦健¹, 钟诚³

1.吉林大学通信工程学院,长春 130012

2.长春工业大学计算机科学与工程学院,长春 130012

3.长春工业大学人文学院,长春 130012

通讯作者：王世刚(1962-),男,教授,博士.研究方向:图像分析,立体视频处理.E-mail:wangshigang@vip.sina.com

作者简介:武伟(1982-),女,博士研究生.研究方向:立体视频处理.E-mail:114188246@qq.com

基金:国家自然科学基金重点项目(61631009); “十三五”国家重点研发计划项目(2017YFB0404800); 中央高校基本科研业务费专项项目

摘要

提出了一种蜂窝式透镜阵列立体元图像的生成方法。首先,通过分析真实透镜的成像原理,建立了成像模型。然后,利用虚拟相机阵列模拟透镜阵列,根据显示端透镜阵列和显示器的参数设置虚拟相机的采集参数。最后,采用投影的方式生成立体元图像阵列。实验结果表明:利用本文方法生成的蜂窝式立体元图像阵列在水平和垂直方向均具有连续的视差变化,且满足子图像与立体元图像之间的投影关系,可以真实再现3D物体的空间信息。本文方法既克服了透镜阵列直接采集存在的空间反转和串扰等问题,又可避免光学采集设备带来的误差,节约成本,可为基于组合成像系统研究提供各种图像来源。

关键词: 通信技术; 组合成像; 透镜阵列; 立体元图像

中图分类号:TN911.73 文献标志码:A 文章编号:1671-5497(2018)01-0290-05

Hexagonal elemental image array generation

WU Wei^1,², WANG Shi-gang¹, ZHAO Yan¹, WEI Jian¹, ZHONG Cheng³

1.College of Communication Engineering, Jilin University, Changchun 130012, China

2. School of Computer Science and Engineering, Changchun University of Technology, Changchun 130012, China

3.School of Humanities,Changchun University of Technology,Changchun 130012,China

Abstract

We present a method to generate the element image based on hexagonal lenslet array. By analyzing the imaging principle of real lens we set up the imaging model first. Then, the pick up process of integral imaging is simulated by virtual camera array and the parameters are set according to the display platform. Finally, the pixel mapping is used to generate the elemental image array. Experimental results show that the hexagonal elemental image array generated by the proposed method has continuous horizontal and vertical parallax, satisfies the mapping between subimage and elemental images and can truly represent the spatial information of 3D objects. The proposed method not only overcomes the problems of pseudoscopic and depth reverse generated by lenslet pick up method, but also avoids the error caused by the optical acquisition equipment. In addition, it can save costs and provides various image sources for integral imaging system.

Keyword: communication technology; integral imaging; lenslet array; elemental image

Show Figures

0 引言

组合成像技术是目前3D领域中研究的热点, 属于真三维立体显示技术, 最早由Lippmann^[1]于1908年提出, 由于当时制造工艺相对落后, 此技术一直停滞不前^{[2, 3, 4]}。近年来, 随着工业生产的发展以及3D影片的热播, 立体显示技术又一次成为国内外学者研究的重点。在众多的3D显示方法中, 组合成像技术的应用前景最广, 它可以为观看者提供连续视差和全真色彩的图像, 而且不需要佩戴任何装置, 记录和重现的三维场景都是以二维图像的方式存储, 使得组合成像技术可以使用现有的图像处理方法来传输和处理。

传统组合成像系统中均使用圆形孔径透镜阵列, 随着微透镜阵列制作工艺的发展, 已出现六边形孔径透镜阵列^[5]。因此, 探索六边形孔径透镜阵列在组合成像系统中的应用, 具有重要的研究意义。首先要生成可用的视频源即立体元图像阵列。

立体元图像的生成可以采用真实拍摄和计算机虚拟生成两种方法^[6]。真实拍摄有两种, 一种是将相机以阵列的形式排列来模拟微透镜阵列的排列结构^{[7, 8, 9]}。该方法需对相机进行标定以保证所有相机的光轴都相互平行且在同一平面, 随着相机数量的增加, 标定的难度也加大。真实拍摄的另一种是透镜阵列直接获取立体元图像阵列, 这种方法简单、易实现, 但存在空间反转和串扰等问题^{[10, 11]}。

本文采用计算机模拟组合成像系统的记录过程, 利用虚拟相机模拟透镜阵列生成立体元图像阵列, 每个透镜元相对独立, 可以有效避免串扰, 且虚拟相机可以直接生成无反转的图像, 因而避免了真实立体显示时的空间反转问题。综上, 利用计算机虚拟生成蜂窝式立体元图像阵列, 可以推进蜂窝式透镜阵列在组合成像系统中应用的研究, 节约成本。

1 基本原理

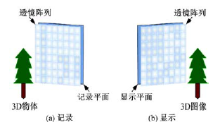
理想的组合成像系统主要有记录和显示两部分组成, 如图1所示。在记录阶段, 微透镜阵列从不同角度获取物体的三维信息, 并将信息以二维图像的形式记录在成像平面上。在显示过程中, 将成像平面放置在微透镜阵列的焦平面上, 根据光路可逆的原理就可以重建物体的三维信息^[12]。

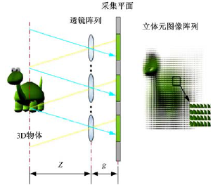
	Figure Option View Download New Window
	图1 理想组合成像系统Fig.1 Ideal integral imaging system

计算机虚拟生成立体元图像阵列的基本原理如图2所示。通过计算得出虚拟3D物体对应每个虚拟透镜元中的视点图像。在计算中, 不考虑有限孔径引起的衍射和离焦引起的模糊。因此, 计算生成的视点图像就是3D物体通过小孔在采集平面的投影。为了避免串扰, 需将计算的视点图像根据虚拟透镜元的大小进行裁剪。通常每个立体元图像的位置和大小与透镜元一致。

	Figure Option View Download New Window
	图2 立体元图像阵列的生成Fig.2 Elemental image generation

2 本文方法

2.1 建立虚拟相机阵列

蜂窝式透镜阵列的每一个透镜元均为六边形, 并以蜂窝状结构紧密排列。传统立体元图像阵列都是采用水平或垂直方向上直接投影的方式, 这对于蜂窝式透镜阵列是不可行的。因此要生成可以用于蜂窝式透镜成像系统的立体元图像阵列, 首先要分析蜂窝式透镜阵列的结构。

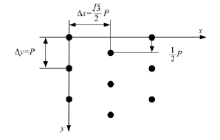
蜂窝式透镜阵列的排列结构如图3所示, 透镜元的水平间距为 $\begin{matrix} \sqrt[]{3} \end{matrix}$ /2P, 其中垂直间距为P。利用虚拟相机模拟透镜元, 设左上角相机中心为原点坐标, 则虚拟相机的空间位置坐标为:

	Figure Option View Download New Window
	图3 蜂窝式透镜阵列排列结构Fig.3 Structure of hexagonal lenslet array

S(i, j)= $\begin{matrix} \{\begin{matrix} (i - 1) P, (j - 1) \frac{\sqrt[]{3}}{2} P \\ j = 1, 3, 5, \dots \\ \frac{P}{2} + (i - 1) P, \frac{\sqrt[]{3}}{2} P + (j - 2) \frac{\sqrt[]{3}}{2} P \\ j = 2, 4, 6, \dots \end{matrix} \end{matrix}$ (1)

生成的蜂窝式虚拟相机矩阵如图4所示。

	Figure Option View Download New Window
	图4 蜂窝式虚拟相机阵列Fig.4 Hexagonal virtual camera array

虚拟相机的焦距、视角与显示平台中蜂窝式透镜阵列的光学参数一致。虚拟相机的分辨率r为:

r= $\begin{matrix} \frac{PM}{H} \end{matrix}$ × $\begin{matrix} \frac{2 \sqrt[]{3} PN}{3 W} \end{matrix}$ (2)

式中:M× N、H× W分别为显示设备的分辨率及外形尺寸。

2.2 参数设置

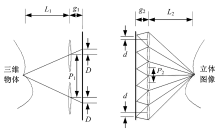
根据显示过程所需的立体元图像阵列的数量、分辨率以及景深等相关参数, 设置物距、虚拟相机的相机间隔、焦距、立体元图像分辨率等参数。具体方法如图5所示。

根据光线光学可以得到:

	Figure Option View Download New Window
	图5 采集端与显示端的关系Fig.5 Relation ship between acquisition and display

$\begin{matrix} \frac{L_{1}}{g_{1}} \end{matrix}$ = $\begin{matrix} \frac{P_{1}}{D} \end{matrix}$ (3)

$\begin{matrix} \frac{L_{2}}{g_{2}} \end{matrix}$ = $\begin{matrix} \frac{P_{2}}{d} \end{matrix}$ (4)

$\begin{matrix} \frac{D}{d} \end{matrix}$ =β (5)

式中:L₁、g₁、P₁、D为采集端的物距、相机焦距、相机阵列镜头间距、相邻立体元图像间视差; L₂、g₂、P₂、d分别为显示端的像距、透镜到显示平面的距离、透镜阵列间距、相邻立体元图像间视差; β 为放大系数。

将其带入组合成像系统横向分辨率R_I、可观测视角θ 和景深Δ Z的关系式中, 即可得到相机阵列记录物距L₁、相机间隔P₁与三维再现像显示特性的关系为:

R_I= $\begin{matrix} \frac{P_{1} g_{1}}{β P_{2} L_{1}} \end{matrix}$ R_d(6)

θ =2arctan $\begin{matrix} (\frac{P_{2}}{2 g_{2}}) \end{matrix}$ (7)

L₂=Nf₂(8)

式中:R_d是显示平面的分辨率; f₂是透镜阵列的焦距。可以由上式建立组合成像系统显示端与采集端的联系, 根据显示端参数设置采集端立体元图像阵列的生成。

2.3 建立投影模型

建立蜂窝式透镜阵列的投影模型, 如图6所示。设相机矩阵为m× n, 单个立体元图像的分辨率为p× q, 则投影后的蜂窝式立体元图像阵列的分辨率R为:

R=m× p+ $\begin{matrix} \frac{1}{2} \end{matrix}$ × p, q+(n-1)× $\begin{matrix} \frac{3}{4} \end{matrix}$ q (9)

虚拟相机中第(i, j)幅立体元图像中的像素点One(x, y)与蜂窝式立体元图像阵列中像素点E(X, Y)的投影关系为:

One(x, y)= $\begin{matrix} \{\begin{matrix} E (X + p (i - 1), Y + \frac{3}{4} q (j - 1)), \\ j = 1, 3, 5 \\ E (X + \frac{1}{2} p + p (i - 1), \\ Y + \frac{3}{4} q + \frac{3}{4} q (j - 2)), j = 2, 4, 6 \end{matrix} \end{matrix}$ (10)

	Figure Option View Download New Window
	图6 虚拟相机阵列与蜂窝式立体元图像阵列的投影模型Fig.6 Pixel mapping between virtual camera array and hexagonal lenslet array

3 实验验证

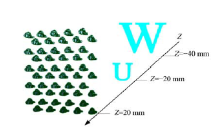
虚拟3D物体由字母“ W” 、“ U” 组成, 距离虚拟透镜阵列的距离Z分别为60、40 mm, 如图7所示。组合成像真实立体显示平台如图8所示。

	Figure Option View Download New Window
	图7 虚拟场景Fig.7 Virtual scene

	Figure Option View Download New Window
	图8 组合成像显示平台Fig.8 Integral imaging display plane

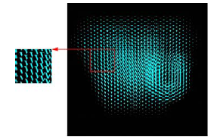
投影仪分辨率为1920× 1080, 与透镜阵列间的距离为56 mm, 像素大小为0.06 mm即R_d≈ 17 pixel/mm。显示端所用的透镜阵列水平间距为 $\begin{matrix} \sqrt[]{3} \end{matrix}$ mm, 垂直间距为2 mm, 焦距f₂=5 mm, 显示模式为深度优先模式g₂=f₂。设P₁=P₂, 则放大系数β =1。如果想生成分辨率为R_I=1.4 pixel/mm, 视角θ =22° , 立体图像深度L₂=165 mm的三维图像, 则由式(6)~(8)可以得到采集端的配置参数为:蜂窝式虚拟相机阵列为39× 34, 虚拟相机焦距g₁=5 mm, 相机水平间距 $\begin{matrix} \sqrt[]{3} \end{matrix}$ mm, 垂直间距2 mm, 立体元图像的分辨率为38× 33。

蜂窝式虚拟相机阵列生成的立体元图像如图9所示。

	Figure Option View Download New Window
	图9 立体元图像Fig.9 Elemental images

根据式(10)将所有立体元图像投影生成蜂窝式立体元图像阵列。

由于本文采用直接投影的方式生成蜂窝式立体元图像阵列, 所以从图10的局部放大图中可以看出, 每个立体元图像都是正立的, 不存在反转, 且立体元图像间也没有串扰的现象。

	Figure Option View Download New Window
	图10 蜂窝式立体元图像阵列Fig.10 Hexagonal elemental image array

将蜂窝式立体元图像阵列放置于组合成像真实立体显示平台, 显示效果如图11所示。

	Figure Option View Download New Window
	图11 真实立体显示效果Fig.11 True stereo display

从真实立体显示效果中可以清晰看到不同视角下的立体图像, 且各视角间的视差明显。例如左右视点间字母U与字母W的间距不同。上下视点间字母U与字母W的相对高度不同。以上实验结果说明, 本文提出的基于蜂窝式透镜阵列的立体元图像阵列生成方法是正确、有效的。

4 结束语

本文提出了一种基于蜂窝式透镜阵列立体元图像阵列的生成方法。利用虚拟相机模拟组合成像系统的记录过程, 根据显示端透镜阵列和显示器的参数设置虚拟相机的采集参数, 采用直接投影的方式生成立体元图像阵列。实验结果表明, 该方法能够生成具有连续水平和垂直视差的蜂窝式立体元图像阵列, 能真实再现3D物体的空间信息。本文方法既克服了透镜阵列直接采集存在空间反转和串扰的问题, 又为基于蜂窝式透镜阵列的研究提供了丰富的图像源。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Lippmann M G. Epreuves reversible donnant la sensatioin du relief[J]. Journal of Physiology, 1908, 1(7): 821-825. [本文引用:1]
[2]	王琼华. 3D显示技术与器件[M]. 北京: 科学出版社, 2011. [本文引用:1]
[3]	Ives H E. Optical properties of alippmann lenticulated sheet[J]. Journal of the Optical Society of America, 1931, 21(3): 171-176. [本文引用:1]
[4]	Okano F, Hoshino H, Arai J, et al. Real-time pickup method for a three-dimensional image based on integral photography[J]. Applied Optics, 1997, 36(7): 1598-1603. [本文引用:1]
[5]	刘德森. 微小光学与微透镜阵列[M]. 北京: 科学出版社, 2013. [本文引用:1]
[6]	Hong J, Kim Y, Choi H J, et al. Three-dimensional display technologies of recent interest: principles, status, and issues[J]. Applied Optics, 2011, 50(34): 87-115. [本文引用:1]
[7]	Javidi B, Sola-Pikabea J, Martinez-Corral M. Breakthroughs in photonics 2014: recent advances in 3-D integral imaging sensing and display[J]. IEEE Photonics Journal, 2015, 7(3): 0700907. [本文引用:1]
[8]	Park S, Yeom J, Jeong Y, et al. Recent issues on integral imaging and its applications[J]. Journal of Information Display, 2014, 15(1): 37-46. [本文引用:1]
[9]	Luo C G, Wang Q H, Deng H, et al. Extended depth of field in integral imaging pick up process based on amplitude modulated sensor arrays[J]. Optics Engineering, 2015, 54(7): 073108-14. [本文引用:1]
[10]	Kishk S, Javidi B. Improved resolution 3D object sensing and recognition using time multiplexed computational integral imaging[J]. Optics Express, 2003, 11(26): 3528-3541. [本文引用:1]
[11]	Hong J, Park J H, Jung S, et al. Depth-enhanced integral imaging by use of optical path control[J]. Optics Letters, 2004, 29(15): 1790-1792. [本文引用:1]
[12]	Arai J, Okano F, Hoshino H, et al. Gradient-index lens-array method based on real-time integral photography for three-dimensional images[J]. Applied Optics, 1998, 37(11): 2034-2045. [本文引用:1]

1908

0.0

... 0 引言组合成像技术是目前3D领域中研究的热点,属于真三维立体显示技术,最早由Lippmann^[1]于1908年提出,由于当时制造工艺相对落后,此技术一直停滞不前^[2,3,4] ...

2011

0.0

1931

0.0

1997

0.0

2013

0.0

... 传统组合成像系统中均使用圆形孔径透镜阵列,随着微透镜阵列制作工艺的发展,已出现六边形孔径透镜阵列^[5] ...

2011

0.0

... 立体元图像的生成可以采用真实拍摄和计算机虚拟生成两种方法^[6] ...

2015

0.0

... 真实拍摄有两种,一种是将相机以阵列的形式排列来模拟微透镜阵列的排列结构^[7,8,9] ...

2014

0.0

... 真实拍摄有两种,一种是将相机以阵列的形式排列来模拟微透镜阵列的排列结构^[7,8,9] ...

2015

0.0

... 真实拍摄有两种,一种是将相机以阵列的形式排列来模拟微透镜阵列的排列结构^[7,8,9] ...

2003

0.0

... 真实拍摄的另一种是透镜阵列直接获取立体元图像阵列,这种方法简单、易实现,但存在空间反转和串扰等问题^[10,11] ...

2004

0.0

... 真实拍摄的另一种是透镜阵列直接获取立体元图像阵列,这种方法简单、易实现,但存在空间反转和串扰等问题^[10,11] ...

1998

0.0

... 在显示过程中,将成像平面放置在微透镜阵列的焦平面上,根据光路可逆的原理就可以重建物体的三维信息^[12] ...