基于多址干扰和蜂窝间互扰分布的多载波系统联合接收方法

引用本文

王金鹏, 曹帆, 贺晓阳, 邹念育. 基于多址干扰和蜂窝间互扰分布的多载波系统联合接收方法[J].吉林大学学报（工学版）, 2018,48(1): 301-305
WANG Jin-peng, CAO Fan, HE Xiao-yang, ZOU Nian-yu. Multi carrier system joint receiving method based on MAI and ICI[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 301-305 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170277
Permissions

基于多址干扰和蜂窝间互扰分布的多载波系统联合接收方法

王金鹏, 曹帆, 贺晓阳, 邹念育

大连工业大学信息学院,辽宁大连 116034

作者简介:王金鹏(1979-),男,副教授,博士.研究方向:下一代网络技术.E-mail:wangjp@dlpu.edu.cn

基金:国家自然科学基金项目(61402069,61272369); 辽宁省普通高等教育本科教学改革立项项目(UPRP20140139); 辽宁省自然科学基金项目(20170540059); 辽宁省教育厅一般项目(2016J205)

摘要

为了研究无线蜂窝系统中下行链路的性能,提出了一种基于最小均方误差和空间分集的多载波系统中下行链路的联合接收方法。由干扰的类高斯特性,给出了多址干扰、蜂窝间互扰、信干燥比和误码率的详细数学表达,最后进行了仿真验证。结果表明:本文方法与仿真结果一致,从而为研究多载波系统下行链路的性能提供了一种新思路。

关键词: 通信技术; 多址干扰; 蜂窝间互扰; 分集; 误码率

中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2018)01-0301-05

Multi carrier system joint receiving method based on MAI and ICI

WANG Jin-peng, CAO Fan, HE Xiao-yang, ZOU Nian-yu

School of Information Science and Engineering, Dalian Polytechnic University, Dalian 116034, China

Abstract

To study the downlink performance of a cellular system, this paper establishes a method of combing Minimum Mean Square Error (MMSE) and location diversity in downlink of multi carrier system. The possible Gaussian interference factors in receiving the composite signals are the keys to express the theoretical conditional Bit Error Rate (BER) in a given set of channel gains. By Gauss properties of the interference, the mathematical expressions of the Multiple Access Interference (MAI), Inter-cellular Interference (ICI), Signal to Interference plus Noise Ratio (SINR) and BET are given, and Monte Carlo simulation method is provided. The simulation results show that the theory and computer simulation method proposed in this paper are effective and feasible.

Keyword: communication technology; multiple access interence(MAI); inter-cellular interference(ICI); diversity; bit error rate(BER)

Show Figures

0 引言

多载波系统由于其信道呈现稀疏特性^[1], 故其在频率选择性的多通道情况下可以拥有较强的对抗性, 同时具有较高的频带利用率, 一直以来都是研究的热点, 并被认为是新一代宽带无线接入的可选方案之一^[2]。伴随着频域中对正交扩频码的应用, 用户数据通过多载波系统的发射装置进行扩频。可以通过频域均衡技术在恶劣的衰落环境中获得较好的误比特率(BER)^{[3, 4]}。当然, 与直接数字序列系统相同的是, 在多载波系统中可以应用频分复用^[5], 也可以通过限制带宽来达到目的。对于移动用户来说, 由于阴影和距离衰落导致的接收信号功率降低可以通过空间分集接收方法来进行补偿^[6]。这些方法均可以提高下行基链路的传输性能。最小均方误差估计(MMSE)方法的主要思想是使误差的均方值最小; 空间分集可以对多个有一定距离的接收天线的信号进行合并接收, 并利用各个天线的不相关特性以达到接收信号最优的效果。

本文提出了一种基于最小均方误差和空间分集的多载波系统中下行链路的联合接收方法, 该方法既具备了空间分集的信号合并最优特性, 又具有MMSE方法所带来的均方误差最小的优势。计算机仿真结果表明, 通过联合使用最小均方误差的频域均衡(MMSE-FDE)和接收分集方法可以极大地提高下行链路的容量^{[7, 8]}。这些通过计算机仿真得到的结论如何在理论上得到验证仍存在着很大的问题^{[9, 10]}, 因此建立一整套的完备的理论体系来评估由空间分集方法建立的下行链路性能就显得尤为重要。

1 系统模型及理论推导

多载波系统中包括正交扩频码、交织码和高斯白噪声等信号, 其中正交扩频码用来确认用户, 而交织码可以用来分离微蜂窝的空间^[11]。频率选择性衰落信道很难在用户中获得完美的正交性^[12], 如图1所示, 子载波的增益不再是恒定的, 这就会带来多址干扰(Multiple access interference, MAI)。

	Figure Option View Download New Window
	图1 复合接收信号Fig.1 Composite received signal

考虑第i个基站BS i与第j个用户u(j)的距离为r_{i_u}₍_j₎, 同时假定阴影衰落因子为α , 遮挡衰落的标准方差为β , 信道为高斯白噪声的理想信道AGWN, 空间分集的天线个数为m, 则信道增益可以表示为:

$\begin{matrix} \{\begin{matrix} H_{i_u (j)}^{(m)} (k) = \overset{L - 1}{\sum_{l = 0}} ξ_{i_u (j), l}^{(m)} \exp (- j 2 πk \frac{τ_{l}}{N_{c}}) \\ Π^{(m)} (k) = n^{(m)} (t) \exp (- j 2 πk \frac{t}{N_{c}}) \end{matrix} \end{matrix}$ (1)

MMSE-FDE的权重为: $\begin{matrix} w_{i_u (j), MMSE}^{(m)} \end{matrix}$ (k)= $\begin{matrix} \frac{Γ_{i_u (j), eff} H_{i_u (j)}^{(m) *} (k)}{\overset{\infty}{\sum_{i = 0}} Γ_{i_u (j), eff} (U + δ u_{i}) \overset{M - 1}{\sum_{m = 0}} {|H_{i_u (j)}^{(m)} (k)|}^{2} + SF} \end{matrix}$ (2)

式中:

Γ _{i_u}₍_j_{), eff}= $\begin{matrix} \frac{S_{i_u (j)} N_{c} T_{c}}{N_{0}} \end{matrix}$ = $\begin{matrix} \frac{E_{s}}{N_{0}} \end{matrix}$ × $\begin{matrix} r_{i_u (j)}^{- α} \end{matrix}$ × 10^-β⁽ⁱ⁾^/¹⁰ (3)

而此时的多址干扰MAI为:

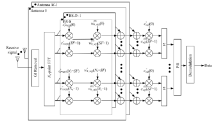
μ _MAI(n)= $\begin{matrix} \frac{1}{SF} \end{matrix} \begin{matrix} \overset{(n + 1) SF - 1}{\sum_{k = nSF}} \end{matrix} \begin{matrix} \overset{M - 1}{\sum_{m = 0}} \end{matrix} \begin{matrix} \overset{D - 1}{\sum_{b = 0}} \end{matrix} \begin{matrix} \underset{u (b) \neq u (j)}{\overset{U + δ u_{b} - 1}{\sum_{u (b) = 0}}} \end{matrix}$ ε _b× $\begin{matrix} \sqrt[]{\frac{2 S_{b_u (j)}}{SF}} \end{matrix} \begin{matrix} {\tilde{H}}_{b_u (j)} \end{matrix}$ (k)c_u₍_b₎(k mod SF)× $\begin{matrix} c_{u (j)}^{*} \end{matrix}$ (k mod SF)d_u₍_b₎(n) (4)

假设多载波系统的子载波数量为N_c, 扩频因子为SF, 图2给出了使用最小均方误差的频域均衡(MMSE-FDE)和接收分集方法联合接收的系统框图, 包括发射和接收两部分。

考虑基站BS i中微蜂窝j的用户u, 其并行数据序列N_c/SF可以从已调信号序列{d_u₍_j₎(n); n=0~N_c/SF-1}中通过串并转换(S/P)得到。S/P转换的输出是通过计算扩频因子SF乘以正交扩频码{C_u₍_j₎(k); k=0~SF-1}得到的。通常, 基站i的交织码{C_PN₍_i₎(k); k=0~N_c-1}是被用作结合每个子载波的用户扩频信号做乘法使用的。不同交织码的作用是将那些接收到的合成信号转化成类白噪声性质, 并可以提取出来不同微蜂窝的空间信息。定义第k路子载波的复合接收信号为:

s_i(k)= $\begin{matrix} \sqrt[]{\frac{2 P_{i}}{SF}} \end{matrix} \begin{matrix} \overset{U + δ u_{i} - 1}{\sum_{u (i) = 0}} \end{matrix}$ d_u₍_i₎ $\begin{matrix} (|\frac{k}{SF}|) \end{matrix}$ ×

c_u₍_i₎(k mod SF)c_PN₍_i₎(k) (5)

$\begin{matrix} \{\begin{matrix} \frac{1}{SF} \overset{SF - 1}{\sum_{k = 0}} c_{u (i)} (k) c_{u (i)}^{*} (k) = δ (u - u') \\ E [c_{PN (i)} (k) c_{PN (i)} (k')] = δ (k - k') \end{matrix} \end{matrix}$ (6)

	Figure Option View Download New Window
	图2 下行链路多载波蜂窝系统发射机/接收机Fig.2 Downlink MC-CDMA transmitter/receiver with site diversity operation

然而, 由于多址干扰(Multiple access interference, MAI)的存在, 多径衰落信道中是没有理想正交性的。多址干扰 MAI 定义如下:

$\begin{matrix} \sqrt[]{\frac{2 S_{b_u (j)}}{SF}} \end{matrix} \begin{matrix} {\tilde{H}}_{b_u (j)} \end{matrix}$ (k)c_u₍_b₎(k mod SF)×

$\begin{matrix} c_{u (j)}^{*} \end{matrix}$ (k mod SF)d_u₍_b₎(n) (7)

式中: $\begin{matrix} {\tilde{H}}_{b_u (j)} \end{matrix}$ (k)= $\begin{matrix} H_{b_u (j)}^{(m)} \end{matrix}$ (k) $\begin{matrix} w_{b_u (j)}^{(m)} \end{matrix}$ (k)。通过式(5)(6)(7)可知方差为:

2 $\begin{matrix} σ_{μ}^{2} \end{matrix}$ (n)= $\begin{matrix} \frac{2}{SF} \end{matrix} \begin{matrix} \frac{N_{o}}{N_{c} T_{c}} \end{matrix}$ [ $\begin{matrix} \frac{1}{SF} \end{matrix} \begin{matrix} \overset{(n + 1) SF - 1}{\sum_{k = nSF}} \end{matrix} \begin{matrix} \overset{D - 1}{\sum_{b = 0}} \end{matrix} \begin{matrix} \overset{m - 1}{\sum_{m = 0}} \end{matrix}$ × $\begin{matrix} {|w_{b_u (f)}^{(m)} (k)|}^{2} \end{matrix}$ + $\begin{matrix} \frac{1}{SF} \end{matrix} \begin{matrix} \frac{E_{s}}{N_{o}} \end{matrix} \begin{matrix} \overset{D - 1}{\sum_{b = 0}} \end{matrix} \begin{matrix} r_{b_u (f)}^{- α} \end{matrix}$ × 10^-β⁽^b⁾^/¹⁰× (U+δ u_b-1){ $\begin{matrix} \frac{1}{SF} \end{matrix} \begin{matrix} \overset{(n + 1) SF + 1}{\sum_{k = nSF}} \end{matrix} \begin{matrix} {|{\dot{H}}_{b_u (f)} (k)|}^{2} \end{matrix}$ -| $\begin{matrix} \frac{1}{SF} \end{matrix} \begin{matrix} \overset{(n + 1) SF - 1}{\sum_{k = nSF}} \end{matrix} \begin{matrix} {\dot{H}}_{k_u (f)} \end{matrix}$ (k)|²}+ $\begin{matrix} \frac{1}{SF} \end{matrix} \begin{matrix} \frac{E_{s}}{N_{o}} \end{matrix} \begin{matrix} \overset{D - 1}{\sum_{b = 0}} \end{matrix} \begin{matrix} \overset{6}{\sum_{i = 0 i \neq b}} \end{matrix} \begin{matrix} r_{i_u (f)}^{- α} \end{matrix}$ × 10^-β⁽^f⁾^/¹⁰× (U+δ l_i) $\begin{matrix} \frac{1}{SF} \end{matrix} \begin{matrix} \overset{(n + 1) SF + 1}{\sum_{k = nSF}} \end{matrix}$ $\begin{matrix} \overset{M - 1}{\sum_{m = 0}} \end{matrix}$ × | $\begin{matrix} w_{b_u (f)}^{(m)} \end{matrix}$ (k) $\begin{matrix} H_{(i_u (f)}^{(m)} \end{matrix}$ (k)|²

另外, 蜂窝间互扰ICI(Inter-cellular interference)是由于交织码不正交而在蜂窝之间产生的, 其可定义为:

2 $\begin{matrix} σ_{ICI}^{2} \end{matrix}$ (n)= $\begin{matrix} \frac{2}{S F^{2}} \end{matrix} \begin{matrix} \overset{D - 1}{\sum_{b = 0}} \end{matrix} \begin{matrix} \underset{i \neq D}{\overset{\infty}{\sum_{i = 0,}}} \end{matrix} \begin{matrix} \frac{S_{i_u (j)}}{SF} \end{matrix}$ (U+δ u_i)× $\begin{matrix} \frac{1}{SF} \end{matrix} \begin{matrix} \overset{(n + 1) SF - 1}{\sum_{k = nSF}} \end{matrix} \begin{matrix} \overset{M - 1}{\sum_{m = 0}} \end{matrix} \begin{matrix} {|w_{b_u (j)}^{(m)} (k) H_{i_u (j)}^{(m)} (k)|}^{2} \end{matrix}$ (8)

信道的增益由本地的平均误码率(BER)表征, 其值是通过统计平均及数值仿真得到的, 可以表示为:

P_e $\begin{matrix} (\frac{E_{b}}{N_{0}}) \end{matrix}$ = $\begin{matrix} \int_{0}^{\infty} \end{matrix}$ … $\begin{matrix} \int_{0}^{\infty} \end{matrix}$ P_e(γ (E_s/N₀|

{ $\begin{matrix} H_{i_u (f)}^{(m)} \end{matrix}$ (k)}))p({ $\begin{matrix} H_{i_u (j)}^{(m)} \end{matrix}$ (k)}) $\begin{matrix} \prod_{m, k, i} \end{matrix}$ d $\begin{matrix} H_{i_u (j)}^{(m)} \end{matrix}$ (k) (9)

由上述假定, 信道增益可表示为{ $\begin{matrix} H_{i_u (j)}^{(m)} \end{matrix}$ (k); k=0~N_c-1; m=0~M-1; i=0~D-1}, 那么在QPSK调制情况下的所有信号“ 1” 均可表示为 $\begin{matrix} \{d_{u (j)} (n) = (1 + j 1) / \sqrt[]{2}\} \end{matrix}$ , 此时的信道BER就可以表示为:

P_e $\begin{matrix} (γ (E_{s} / N_{0} | \{H_{i_u (j)}^{(m)} (k)\})) \end{matrix}$ = $\begin{matrix} \frac{1}{2} \end{matrix}$ Pr(Re[y_u₍_j₎(n)]< 0|{ $\begin{matrix} H_{i_u (j)}^{(m)} \end{matrix}$ (k)})+ $\begin{matrix} \frac{1}{2} \end{matrix}$ Pr(Im[y_u₍_j₎(n)]< $\begin{matrix} 0 | {{H^{(m)}}_{i_u (j)} \end{matrix}$ (k)})= $\begin{matrix} \frac{1}{2} \end{matrix}$ erfc( $\begin{matrix} \sqrt[]{\frac{γ (E_{s} / N_{0} | H_{i_u (j)}^{(m)} (k))}{4}} \end{matrix}$ ) (10)

式中:erfc(x)= $\begin{matrix} \frac{2}{\sqrt[]{π}} \end{matrix} \begin{matrix} \int_{x}^{\infty} \end{matrix}$ exp(-t²)dt。

2 仿真实验

表1为仿真环境和各个相关仿真参数的设定值。

表1 仿真条件设定 Table 1 Simulation condition

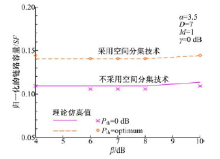
从图3可以看出, 遮挡衰减系数β 的增大对于下行链路容量几乎没有影响。但是β 的增加可以引起干扰功率增大, 从而使得干扰发生的概率也变大, 因此下行链路的容量降低了。

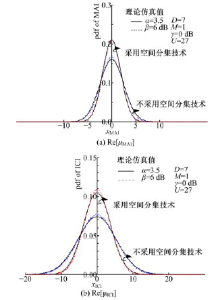
	Figure Option View Download New Window
	图3 阴影衰落 β 对下行链路容量的影响Fig.3 Effect of shadowing loss standard deviation β on downlink capacity

通过空间分集算法后, 接收信号的功率有了明显增强, 说明β 的微小变化可以通过混合分集算法补偿回来, 理论分析结果与仿真结果是一致的。由信干噪比和误码率看出干扰成分为复高斯随机变量。图4给出了MAI的概率密度函数(Probability density functions, PDF)的仿真结果。假定每个蜂窝的用户数U =27 , γ = 0 dB 代表信道中的是归一化的功率延迟, P_th=4.5 dB, 零均值的高斯分布符合MAI的PDF要求, 同时满足了理论计算的近似值。

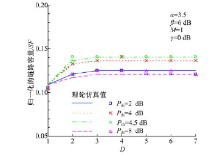
图5给出了采用本文方法时多载波系统的性能, 可以看出, 随着参与空间分集的基站数量的增加, 多载波下行链路的容量也在增加, 说明本文的联合接收方法是有效的。分集使用的基站数目刚好时系统性能达到最佳(比如图5中的基站数为4), 此时再增加基站数量反而会降低系统性能。

	Figure Option View Download New Window
	图4 MAI和ICI的概率密度分布Fig.4 Distributions of MAI and ICI components

	Figure Option View Download New Window
	图5 联合接收方法的下行链路系统容量Fig.5 Downlink capacity based on joint receiving method

3 结束语

本文首先在理论上准确描述在高斯干扰下接收信号的基础表达, 其次推演并计算出信道的理论误码率, 最后采用蒙特卡洛数值仿真方法对平均误码率的条件进行模拟并获得当前的平均误码率, 以此来判断在给定的条件下信道增益是否能够达到标准。文中给出了局部平均误码率的累积分布的中断概率, 定义了下行链路的容量, 并对理论和计算机仿真结果进行了分析和比较, 实验证明本文理论模型准确, 数学描述完备, 为研究多载波系统下行链路的性能提供了一种有效的理论方法。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Li Sheng-bao, Li Ren-jie, Wang Jian-qiang, et al. Stabilizing periodic control of automated vehicle platoon with minimized fuel consumption[J]. IEEE Transactions on Transportation Electrification, 2017, 3(1): 259-271. [本文引用:1]
[2]	Tian Pei-gen, Xiao Xi, Wang Kui, et al. A hierarchical energy management system based on hierarchical optimization for microgrid community economic operation[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 2230-2241. [本文引用:1]
[3]	Chen Jie, Li Jia-hong, Yang Shuang-hua, et al. Weighted optimization-based distributed Kalman filter for nonlinear target tracking in collaborative sensor networks[J]. IEEE Transactions on Cybernetics, 2017(99): 1-14. [本文引用:1]
[4]	Li P, Li M, Feng J. Multi-feedback interference cancellation algorithms for OFDM systems over doubly-selective channels[J]. Algorithms, 2015, 8(3): 484-513. [本文引用:1]
[5]	Vasudevan K. Coherent detection of turbo-coded OFDM signals transmitted through frequency selective Rayleigh fading channels with receiver diversity and increased throughput[J]. Wireless Personal Communications, 2015, 82(3): 1623-1642. [本文引用:1]
[6]	Shu S, Qu D, Li L, et al. Invertible subset QC-LDPC codes for PAPR reduction of OFDM signals[J]. IEEE Transactions on Broadcasting, 2015, 61(2): 290-298. [本文引用:1]
[7]	Zhang L, Liu B, Xin X, et al. Joint robustness security in optical OFDM access system with turbo-coded subcarrier rotation[J]. Opt Express, 2015, 23(1): 13-18. [本文引用:1]
[8]	Wan L, Zhou H, Xu X, et al. Adaptive modulation and coding for underwater acoustic OFDM[J]. IEEE Journal of Oceanic Engineering, 2015, 40(2): 327-336. [本文引用:1]
[9]	Marina M, Arno T, Emmeric T, et al. Diversity performance of off-body MB-OFDM UWB-MIMO[J]. IEEE Transactions on Antennas & Propagation, 2015, 63(7): 3187-3197. [本文引用:1]
[10]	Chai E, Shin K. Low-overhead control channels in wireless networks[J]. IEEE Transactions on Mobile Computing, 2015, 14(11): 2303-2315. [本文引用:1]
[11]	Wang Jin-peng, Zou Nian-yu, Zhang Yun-cui, et al. Study on downlink performance of multiple access algorithm based on antenna diversity[J]. ICIC Express Letters, 2015, 9(4): 1221-1225. [本文引用:1]
[12]	力智, 胡学龙. 单载波与多载波调制系统中调制识别算法研究[J]. 国外电子测量技术, 2016, 35(11): 73-75. Li Zhi, Hu Xue-long. Research of modulation recognition algorithm in the single carrier and multicarrier modulation system[J]. Foreign Electronic Measurement Technology, 2016, 35(11): 73-75. [本文引用:1]

2017

0.0

... 0 引言多载波系统由于其信道呈现稀疏特性^[1],故其在频率选择性的多通道情况下可以拥有较强的对抗性,同时具有较高的频带利用率,一直以来都是研究的热点,并被认为是新一代宽带无线接入的可选方案之一^[2] ...

2016

0.0

... 可以通过频域均衡技术在恶劣的衰落环境中获得较好的误比特率(BER)^[3,4] ...

2015

0.0

... 可以通过频域均衡技术在恶劣的衰落环境中获得较好的误比特率(BER)^[3,4] ...

2015

0.0

... 当然,与直接数字序列系统相同的是,在多载波系统中可以应用频分复用^[5],也可以通过限制带宽来达到目的 ...

2015

0.0

... 对于移动用户来说,由于阴影和距离衰落导致的接收信号功率降低可以通过空间分集接收方法来进行补偿^[6] ...

2015

0.0

... 计算机仿真结果表明,通过联合使用最小均方误差的频域均衡(MMSE-FDE)和接收分集方法可以极大地提高下行链路的容量^[7,8] ...

2015

0.0

... 计算机仿真结果表明,通过联合使用最小均方误差的频域均衡(MMSE-FDE)和接收分集方法可以极大地提高下行链路的容量^[7,8] ...

2015

0.0

... 这些通过计算机仿真得到的结论如何在理论上得到验证仍存在着很大的问题^[9,10],因此建立一整套的完备的理论体系来评估由空间分集方法建立的下行链路性能就显得尤为重要 ...

2015

0.0

2015

0.0

... 1 系统模型及理论推导多载波系统中包括正交扩频码、交织码和高斯白噪声等信号,其中正交扩频码用来确认用户,而交织码可以用来分离微蜂窝的空间^[11] ...

2016

0.0

. 2016, 35(11):73-75

Research of modulation recognition algorithm in the single carrier and multicarrier modulation system

单载波与多载波调制系统中调制识别算法研究

Li Zhi , Hu Xue-long.

力智, 胡学龙

首先叙述了调制识别技术在通信对抗中的研究意义、单载波与多载波调制的通信调制系统和灵巧通信对抗,然后介绍了无线数字信号的调制样式识别的研究现状。为了能够为灵巧通信对抗打下良好的基础,很好地实现单载波与多载波调制系统中信号特征的类间、类内识别是十分重要的。提出了一种用于识别串行单载波和并行多载波的调制样式识别算法,此算法能够对快变瑞利信道下完成MPSK和OFDM的调制样式识别。仿真结果表明,在信噪比为7dB时,识别正确率可以达到90%以上。

... 频率选择性衰落信道很难在用户中获得完美的正交性^[12],如图1所示,子载波的增益不再是恒定的,这就会带来多址干扰(Multiple access interference,MAI) ...