引用本文
刘云, 康冰, 侯涛, 王柯, 刘富. 优化初值的 C均值算法 [J].吉林大学学报（工学版）, 2018,48(1): 306-311
LIU Yun, KANG Bing, HOU Tao, WANG Ke, LIU Fu. Optimal initialization-based C-means method [J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 306-311  
Doi:10.13229/j.cnki.jdxbgxb20161193
Permissions
Copyright©2018, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
优化初值的 C均值算法
刘云, 康冰, 侯涛, 王柯, 刘富
吉林大学 通信工程学院,长春 130022
通讯作者：刘富(1968-),男,教授,博士生导师.研究方向:计算机视觉及模式识别.E-mail:liufu@jlu.edu.cn

作者简介:刘云(1989-),男,博士研究生.研究方向:模式识别及生物信息学.E-mail:liuyun11@mails.jlu.edu.cn

基金:国家自然科学基金项目(61503151); 吉林省自然科学基金项目(10100505); 吉林省重点科技攻关项目(20140204046GX)
摘要

针对 C均值算法( C-means method,CM)对初值敏感、易陷入局部最优的问题,提出一种优化初值的 C均值算法(Optimal initialization-based CM,OICM)。该算法首先计算数据集中每个点的邻域以及邻域密度,选择具有最大邻域密度的点作为第一个聚类中心;然后,从剩余的数据集中选择具有最大邻域密度、且其邻域与已有聚类中心的邻域的连接度满足一定条件的点作为下一个聚类中心,以此类推,直到确定了 C个聚类中心;最后,利用 C均值算法完成数据集的聚类分析。在仿真数据集和UCI数据集上进行聚类实验,结果表明OICM算法有效地克服了传统 C均值算法对初值敏感的缺点,且性能优于其他3种典型的全局 C均值算法。

关键词: 计算机应用; C均值算法; 初值敏感; 邻域密度
中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2018)01-0306-06
Optimal initialization-based C-means method
LIU Yun, KANG Bing, HOU Tao, WANG Ke, LIU Fu
College of Communication Engineering, Jilin University, Changchun 130022, China
Abstract

C-means Clustering Method (CM) is a widely for data clustering, which is sensitive to the initial cluster centers and easily leads to local optimum. To solve this problem, an Optimal Initialization-based C-means Method (OI-CM) is proposed. First for each point in the dataset, the neighborhood and neighborhood density are calculated, and the point with the maximum neighborhood density is selected as the first cluster center. Then, the point with the maximum neighborhood density from the rest datasets is selected as the next cluster center, whose neighborhood must have little coupling degree with the neighborhoods of existing cluster centers. This procedure is continued until all the cluster centers are selected. Finally, the CM is utilized to cluster the datasets with the selected cluster centers. Experimental results on simulated and UCI datasets show that the proposed OI-CM can effectively solve the sensitivity defect of the traditional CM to initial cluster centers, and has superior performance than other three global CMs.

Keyword: computer application; C-means method; initial value sensitivity; neighborhood density
0 引 言

C均值算法(C-means method, CM)是一种常用的聚类算法, 目前已被广泛应用于图像分割[1, 2]、网络入侵检测[3]、文本聚类[4]、混合动力汽车能量管理策略[5]等方向。然而, 传统的C均值算法随机地选择数据集中的样本作为初始聚类中心, 因此, 该算法对初值敏感, 易陷入局部最优[6]。

到目前为止, 已经有很多方法用于解决传统C均值算法的初值敏感问题。例如, Krishna等[6]和Laszlo等[7]利用遗传算法为C均值算法确定初始聚类中心; Likas等[8]提出了一种全局C均值算法, 首先以数据集中全体样本的均值作为第一个聚类中心, 然后分别以第一个聚类中心和数据集中任意一个样本作为初始聚类中心, 以2为聚类个数运行C均值算法, 选择具有最好的聚类结果的样本作为第二个聚类中心, 以此类推, 直到确定了C个聚类中心。该方法的缺点是在聚类中心的选取过程中需要运行许多次C均值算法, 十分费时。基于此, Bagirov[9]和Bai等[10]分别提出了一种快速的全局C均值算法。

由于C均值算法是一种基于中心的聚类算法, 理想的聚类中心应处于样本密度较大的区域, 因此, 基于样本密度的方法是一种有效的确定初始聚类中心的方法。例如, Cao等[11]提出了一种基于邻域模型的初值选取方法, 该方法选择一组具有最大邻域紧密度且彼此之间具有一定分离度的样本作为初始聚类中心, 然而由于该方法利用粗糙集理论中邻域的上下近似集的比值作为某样本的邻域密度, 因此计算过程比较费时; Fatemi等[12]提出了一种基于密度的初值选取方法, 该方法在确定下一个聚类中心时, 需要计算每个样本与现有聚类中心的距离, 因此, 计算过程比较费时。此外, 国内的谢娟英等[13]和赖玉霞等[14]分别提出了基于样本空间分布密度的初始化方法。这类方法都是选择具有较大样本密度且彼此之间相距较远的样本作为初始聚类中心, 区别之处在于计算样本密度的方法以及“ 相距较远” 的定义方法。

为了解决传统C均值算法对初值敏感的问题, 本文提出一种优化初值的C均值算法(Optimal initialization-based CM, OICM)。首先, 计算数据集中每个样本的邻域及邻域密度; 其次, 选择具有最大邻域密度的样本作为第一个聚类中心; 然后, 从剩余的样本中选择具有最大邻域密度且其邻域与已有聚类中心的邻域的连接度满足一定条件的样本作为第二个聚类中心, 以此类推, 直到确定了C个聚类中心; 最后, 利用C均值算法完成聚类分析。该方法的基本假设是某样本的邻域密度越大, 表明该样本所处区域的样本密度越大, 则该样本处于类中心区域的可能性就越大。同时, 为了避免在同一个类中选择多个聚类中心, 各聚类中心的邻域的连接度应小于某个数值。在仿真数据集和UCI数据集上进行聚类实验, 并与传统C均值算法和3种典型的全局C均值算法进行对比, 实验结果表明, OICM算法有效地克服了传统C均值算法对初值敏感的缺点, 且在达到收敛需要的迭代次数和运算时间方面具有一定的优势。

1 C均值算法简述

C均值算法是一种基于中心的聚类算法, C是聚类个数。对于一个给定数据集X= x1, x2, …, xN, C均值算法将其中的每一个样本分配到距离其最近的聚类中。该算法的代价函数为:

J= ∑i=1Nminj=1, 2, …, cd xi, θj2(1)

式中:N为样本数量; d xi, θj代表数据集中第i个样本xi与第j个聚类中心θ j之间的距离测度, 一般利用欧氏距离。

在C均值算法中, 以属于某一类的所有样本的均值作为该类的聚类中心, 定义为:

θ j= 1Nj∑xi∈Cjxi(2)

式中:Cj代表第j个聚类; Nj代表聚类Cj中包含的样本个数, 且满足 ∑j=1cNj=N。

综上, C均值算法的聚类流程可总结为:

(1)随机选择C个样本作为初始的聚类中心。

(2)将所有样本分配到距离其最近的聚类中。

(3)根据式(2)更新各个聚类的聚类中心。

(4)重复步骤(2)和(3)直到所有样本的归属不再变化。

2 本文算法

本文算法首先计算每个样本的邻域及邻域密度, 从中选择C个具有最大邻域密度的样本作为初始聚类中心, 同时聚类中心的邻域之间应保持较小的结合度, 以保证各个聚类中心分别代表不同的类; 最后利用C均值算法对数据集进行聚类分析。

2.1 初值优化

假设X是归一化之后的数据集, 对于任意的x∈ X, 其邻域δ (x)定义为:

δ (x)= xi|xi∈X且d(x, xi)≤ε(3)

式中:ε 为数据集中样本之间距离的平均值, 定义如下:

ε = 2N(N-1)∑i=1N-1∑j=i+1Nd(xi, xj)(4)

样本x的邻域δ (x)的密度Density(δ (x))定义为:

Density(δ (x))= |δ(x)|∑xi∈δ(x)d(x, xi)(5)

式中:|δ (x)|是样本x邻域中的样本个数。可看出, 样本x的邻域密度是指其邻域中样本与x的距离的算术平均值的倒数。样本x的邻域中样本与x的平均距离越小, 样本x的邻域密度就越大, 说明该样本所处区域的样本密度越大, 则该样本处于聚类中心位置的可能性就越大。因此, 本文主要依据样本的邻域密度来选择聚类中心。

如果某样本具有较大的邻域密度, 那么该样本附近的样本同样具有较大的邻域密度。为了在一个聚类中只选择一个聚类中心, 两个聚类中心之间应保持一定的分离程度。本文利用两个样本邻域之间的连接度来衡量两个样本的分离程度, 样本xi的邻域δ (xi)与样本xj的邻域δ (xj)之间的连接度Coupling(δ (xi), δ (xj))定义为:

Coupling(δ (xi), δ (xj))= δ(xi)⋂δ(xj)δ(xi)⋃δ(xj)(6)

式中:|A|表示集合A中包含的样本个数, 两个样本的邻域连接度是指这两个样本的邻域交集中的样本个数与并集中的样本个数的比值。因此, 由式(6)可得:

0≤ Coupling(δ (xi), δ (xj))≤ 1(7)

两个样本邻域之间的连接度越小, 这两个样本属于不同聚类的可能性就越高。在文献[11]中, 数据集中所有样本间的平均距离被用作阈值来判断两个样本是否属于同一个聚类。因此, 如果Coupling(δ (xi), δ (xj))< ε , 则认为xi和xj属于不同聚类的可能性就越大; 反之, 则认为xi和xj属于相同聚类的可能性就越大。

综上所述, 本文算法选择初始聚类中心的流程可总结为:

(1)将数据集X归一化到区间 0, 1, 初始化聚类中心集合Θ =∅。

(2)计算参数ε , 每个样本xi的邻域δ (xi)以及邻域密度Density(δ (xi))。

(3)选择具有最大邻域密度的样本x作为第一个聚类中心, Θ = x。

(4)寻找下一个最大邻域密度的样本x', Density(δ (x'))=max{Density(δ (xi))|xi∈ X-Θ }。

(5)如果对于任意的θ ∈ Θ , 都满足Coupling(δ (x'), δ (θ ))< ε , 则选择样本x'作为下一个聚类中心, Θ =Θ ∪ x'; 否则, Density(f(x'))=0。

(6)重复步骤(4)和(5), 直到 Θ=C, 即选择了C个聚类中心。

2.2 C均值聚类和算法的复杂度分析

以2.1节中选择的C个聚类中心作为初始聚类中心, 利用C均值算法进行聚类分析。

本文算法的复杂度由初值选择和C均值算法的复杂度两部分组成。初值选取过程中的计算量主要来自于N(N-1)/2次距离计算, 因此这部分的复杂度为T(N)=o(N2)。C均值算法的算法复杂度是T(N)=o(NCn), 其中n为迭代次数。

因此, 本文算法的复杂度为T(N)=o(N2)。

3 实验结果
3.1 实验数据

为了验证本文算法的性能, 人工构建了两个具有高斯分布的2维数据集D1和D2。数据集D1共包含有来自两个类的1000个点, 每个类包含500个点; 数据集D2共包含有来自3个类的900个点, 每个类包含300个点。此外, 从UCI数据库(http:∥archive.ics.uci.edu/ml/)下载了3个数据集Iris、Liver Disorders和Pima Indians Diabetes。本文使用的数据集的具体信息如表1所示。在这些数据集上进行聚类实验, 以验证本文算法的性能, 并与传统C均值算法、文献[8]、文献[9]和文献[11]中的方法进行性能对比。

表1 本文选用的数据集信息 Table 1 Information of selected datasets in this paper
3.2 评价标准

使用与文献[9]相同的3个标准来评价本文算法的全局最优性能:

(1)聚类算法最终的代价函数值与理想代价函数值之间的误差, 定义为:

E= J-JoptJopt× 100(8)

式中:J是聚类算法最终得到的代价函数值; Jopt是理想的代价函数值。E=0代表某一种算法找到了数据集的全局最优解。一般地, 如果0< E< 1, 则认为该算法找到了数据集的近似全局最优解[9]。

(2)迭代次数N, 指聚类算法达到收敛所需的循环次数。

(3)运行时间t, 包括初值选取和聚类所需的运算时间。

3.3 仿真数据集实验结果

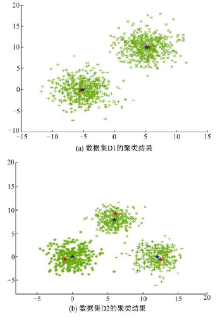
利用本文算法对仿真数据集D1和D2进行聚类分析, 结果分别如图1(a)和(b)所示。在图1中, 相同标记的点被聚为了一类, 红色的五角星是本文算法选取的初始聚类中心, 蓝色的五角星是最终的聚类中心。可以看到, 利用本文算法所选择的初始聚类中心都能较好的代表各自所属的聚类, 且与最终的聚类中心相距十分接近。

表2列出了利用本文算法对数据集D1和D2进行聚类分析时, 选择的初始聚类中心、最终聚类中心以及算法的迭代次数。可以看到, 由于初始聚类中心和最终聚类中心之间相距十分接近, 本文算法分别仅用了2次和3次迭代就在数据集D1和D2上取得了收敛。

表2 初始、最终聚类中心以及达到收敛所需的迭代次数 Table 2 Initial and final cluster centers, and iteration number

图1 本文算法在仿真数据集D1和D2上的聚类结果Fig 1 Cluster results of proposed method on synthetic dataset D1 and D2

将本文算法与未经初值优化的传统C均值算法进行对比, 结果如表3所示。传统的C均值算法随意地选择初始聚类中心, 因此, 本文运行10次该算法, 取迭代次数和运行时间的平均值与本文算法进行对比。从表3可以看到, 由于对初值进行了优化, 本文算法的迭代次数少于传统算法, 然而, 运算时间也长于传统算法。

表3 仿真数据集中初始聚类中心优化前后的结果对比 Table 3 Results comparison of initial cluster centers before and after optimization in synthetic datasets
3.4 UCI数据集实验结果

本文算法在UCI数据集上的聚类结果如表4所示, 包含初始、最终聚类中心, 算法达到收敛的迭代次数以及分类准确率。由于2或3都是Iris数据集合理的聚类个数, 因此本文分别以2和3作为聚类个数进行聚类实验。在Iris数据集的两组聚类结果中, 本文算法分别仅经历3次和2次迭代就取得了收敛, 分类准确率分别是98%和87.33%。在数据集Live Disorders上, 本文算法经历7次迭代达到收敛, 聚类准确率为55.07%; 在数据集Pima Indians Diabetes上, 本文算法经历15次迭代达到收敛, 分类准确率为66.02%。

表4 本文算法在UCI数据集上的聚类结果 Table 4 Clustering results of proposed method on UCI datasets

将本文算法与传统C均值算法、两种全局C均值算法GKM[8]和MGKM[9], 以及基于密度的初值选取方法[11]进行对比, 结果如表5所示。表5中, N为迭代次数, t为运算时间, 单位为秒。所有数据集理想的代价函数值Jopt和GKM、MGKM算法的实验结果都来自文献[9]。传统C均值算法由于随机地选择初始聚类中心, 因此未能在Iris数据集上寻找到全局最优点, 此外其平均的迭代次数也多于本文算法。GKM算法和MGKM算法在数据集Iris和Pima Indians Diabetes上成功地搜索到了全局最优点, 然而在Live Disorders数据集上经过60000次迭代依然没有实现全局最优。本文算法在数据集Iris(C=2)、Pima Indians Diabetes和Live Disorders, 都找到了近似的全局最优点。值得注意的是, 本文算法达到收敛所需的迭代次数远小于GKM和MGKM算法, 仅需要几次或十几次。本文算法与文献[11]中的算法具有相近的全局最优性能和迭代次数, 但是本文算法的运算时间远远小于文献[11]中的算法。

表5 本文算法与传统C均值算法、GKM算法、MGKM算法以及文献[11]中算法在UCI数据集上的性能对比 Table 5 Comparative results of proposed method, traditional c-means method, GKM, MGKM and method in ref.[11] on UCI datasets
4 结束语

为了解决了传统C均值算法(C-means method, CM)对于初值敏感的问题, 本文提出了一种优化初始条件的C均值算法(Optimal Initialization-based CM, OICM)。与传统的C均值算法随机选择初始聚类中心的方式不同, 本文算法依据数据点的邻域密度确定初始聚类中心, 被确定为初始聚类中心的数据点具有较大的邻域密度且彼此之间的邻域连接度小于数据集中数据点间距离的平均值。本文在2个仿真数据集和3个UCI数据集上进行聚类实验, 实验结果表明, 本文算法有效地克服了传统C均值算法对初值敏感的缺点。此外, 本文还在UCI数据集上与3种全局C均值算法进行性能对比, 结果表明本文算法在达到收敛所需的迭代次数和运算时间方面具有一定的优势。

The authors have declared that no competing interests exist.

参考文献
[1] 邢涛, 黄友红, 胡庆荣, 等. 基于动态K均值聚类算法的SAR图像分割[J]. 中国科学院大学学报, 2016, 33(5): 674-678.
Xing Tao, Huang You-hong, Hu Qing-rong, et al. SAR image segmentation based on dynamical K-means clustering algorithm[J]. Journal of University of Chinese Academy of Sciences, 2016, 33(5): 674-678. [本文引用:1]
[2] 李昌兴, 黄艳虎, 支晓斌, 等. 基于加速k均值的谱聚类图像分割算法改进[J]. 传感器与微系统, 2016, 35(9): 137-140.
Li Chang-xing, Huang Yan-hu, Zhi Xiao-bin, et al. Improvements of acceleration k-means based spectral clustering algorithm for image segmentation[J]. Transducer and Microsystem Technologies, 2016, 35(9): 137-140. [本文引用:1]
[3] 刘华春, 候向宁, 杨忠. 基于改进K均值算法的入侵检测系统设计[J]. 计算机技术与发展, 2016, 26(1): 101-105.
Liu Hua-chun, Hou Xiang-ning, Yang Zhong. Design of intrusion detection system based on improved K-means algorithm[J]. Computer Technology and Development, 2016, 26(1): 101-105. [本文引用:1]
[4] 徐森, 卢志茂, 顾国昌. 结合K均值和非负矩阵分解集成文本聚类算法[J]. 吉林大学学报: 工学版, 2011, 41(4): 1077-1082.
Xu Sen, Lu Zhi-mao, Gu Guo-chang. Integrating K-means and non-negative matrix factorization to ensemble document clustering[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(4): 1077-1082. [本文引用:1]
[5] 詹森, 秦大同, 曾育平. 基于遗传优化K均值聚类算法工况识别的混合动力汽车能量管理策略[J]. 中国公路学报, 2016, 29(4): 130-137, 152.
Zhan Sen, Qin Da-tong, Zeng Yu-ping. Energy management strategy of HEV based on driving cycle recognition using genetic optimized K-means clustering algorithm[J]. China Journal of Highway and Transport, 2016, 29(4): 130-137, 152. [本文引用:1]
[6] Krishna K, Murty M N. Genetic K-means algorithm[J]. IEEE Transactions on Systems Man & Cybernetics Part B: Cybernetics, 1999, 29(3): 433-439. [本文引用:2]
[7] Laszlo M, Mukherjee S. A genetic algorithm using hyper-quadtrees for low-dimensional K-means clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(4): 533-543. [本文引用:1]
[8] Likas A, Vlassis N, Verbeek J J. The global K-means clustering algorithm[J]. Pattern Recognition, 2002, 36(2): 451-461. [本文引用:2]
[9] Bagirov A M. Modified global K-means algorithm for minimum sum-of-squares clustering problems[J]. Pattern Recognition, 2008, 41(10): 3192-3199. [本文引用:3]
[10] Bai L, Liang J, Sui C, et al. Fast global K-means clustering based on local geometrical information[J]. Information Sciences, 2013, 245(10): 168-180. [本文引用:1]
[11] Cao F, Liang J, Jiang G. An initialization method for the K-means algorithm using neighborhood model[J]. Computers & Mathematics with Applications, 2009, 58(3): 474-483. [本文引用:2]
[12] Fatemi S B, Mobasheri M R, Abkar A A. Improving the accuracy of multispectral image clustering by means of a new initializing method[J]. Journal of the Indian Society of Remote Sensing, 2016, 44(4): 643-650. [本文引用:1]
[13] 谢娟英, 郭文娟, 谢维信, 等. 基于样本空间分布密度的初始聚类中心优化K-均值算法[J]. 计算机应用研究, 2012, 29(3): 888-892.
Xie Juan-ying, Guo Wen-juan, Xie Wei-xin, et al. K-means clustering algorithm based on optimal initial centers related to pattern distribution of samples in space[J]. Application Research of Computers, 2012, 29(3): 888-892. [本文引用:1]
[14] 赖玉霞, 刘建平. K-means算法的初始聚类中心的优化[J]. 计算机工程与应用, 2008, 44(10): 147-149.
Lai Yu-xia, Liu Jian-ping. Optimization study on initial center of K-means algorithm[J]. Computer Engineering and Applications, 2008, 44(10): 147-149. [本文引用:1]