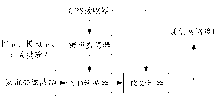基于压缩传感的高精度同步相量测量方法

引用本文

于华楠, 杜瑶, 郭树旭. 基于压缩传感的高精度同步相量测量方法[J].吉林大学学报（工学版）, 2018,48(1): 312-318
YU Hua-nan, DU Yao, GUO Shu-xu. High-precision synchronous phasor measurement based on compressed sensing[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 312-318 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161043
Permissions

基于压缩传感的高精度同步相量测量方法

于华楠^1,², 杜瑶¹, 郭树旭²

1.东北电力大学信息工程学院,吉林省吉林市132012

2.吉林大学电子科学与工程学院,长春 130012

作者简介:于华楠(1981-),女,副教授,博士研究生. 研究方向:压缩传感理论,水声通信和无线通信信道估计.E-mail:yhn810117@163.com

基金:国家自然科学基金项目(51307020); 吉林省科技厅项目(20160520089JH)

摘要

为了消除或减小采用GPS定时的同步相量测量中非精确同步采样所造成的测量误差,提出一种基于压缩传感理论修正离散傅里叶变换估计结果的高精度同步相量测量算法。该算法利用离散傅里叶变换对测量信号进行稀疏化,并采用狄利克雷矩阵为观测矩阵,通过压缩传感重构算法重构测量信号。仿真结果表明:与传统离散傅里叶变换方法相比,该算法在不需要延长测量时间的条件下能够有效消除或减小频谱泄露等误差,并在很大程度上提高了信号的相量测量精度。

关键词: 信息处理技术; 离散傅里叶变换; 压缩传感; 相量测量; 重构算法

中图分类号:TM93 文献标志码:A 文章编号:1671-5497(2018)01-0312-07

High-precision synchronous phasor measurement based on compressed sensing

YU Hua-nan^1,², DU Yao¹, GUO Shu-xu²

1.College of Information Engineering,Northeast Dianli University,Jilin 132012,China

2.College of Electronic Science and Engineering,Jilin University,Changchun 130012,China

Abstract

GPS timing synchronization phasor measurement provides important basis for online analysis of wide-area power signal. Currently discrete Fourier transform method is widely used in synchronization phasor measurement. To eliminate or weaken the measurement error caused by the imprecise synchronous sampling, a high precision synchronous phasor measurement algorithm is proposed. It is based on Compressed Sensing (CS) theory, which modifies discrete Fourier transform to estimate the results. The reconstruction algorithm uses the discrete Fourier transform to rarefy the measuring signal, and takes the Dirichlet matrix as the observation matrix. It also refacors measurement signal with CS refactor algorithm. The simulation results show that, compared with the traditional discrete Fourier transform method, without extending the measurement time, the proposed algorithm can effectively eliminate or weaken the spectrum leakage error and greatly improve the phasor measurement precision of signal.

Keyword: information processing technology; discrete Fourier transform; compressive sensing; phasor measurement; reconstruction algorithm

Show Figures

0 引言

广域测量系统(Wide area measurement system, WAMS)作为电网动态实时监测的新技术和重要手段, 能实时地反映全网系统的动态变化, 对电网的安全稳定运行起到了重要的作用^[1]。而基于GPS技术的同步相量测量单元(Phasor measurement unit, PMU)正是WAMS系统的核心与基础^{[2, 3]}, 并已被广泛应用在电网中以获得电网的实时动态变化, 为实现电力系统动态监测提供了可能。

目前, 国内外学者提出了多种同步相量测量算法, 主要包括离散傅里叶变换(Discrete Fourier transform, DFT)法^[4]、过零点检测法(Zero crossing technique)^[5]和数字滤波器法^{[6, 7]}等。其中, 由于DFT算法适用于快速运算, 且具有良好的谐波抑制特性, 在静态条件下具有较好应用价值, 而被广泛应用到同步相量测量中。但在非同步采样的情况下, 现有的DFT算法往往会在幅值和频率测量上出现误差, 且误差会随着非同步性的增强而急剧增大, 导致出现频谱泄露和栅栏效应, 使温测量结果达不到实际应用的要求^[8]。因此, 这种误差使DFT算法存在一定的局限性, 降低了相量测量的准确度, 以至于直接影响到WAMS的应用效果。同步相量的不准确测量最终将导致电网的动态安全监控能力下降, 严重时将影响电网的安全稳定运行^[9]。

本文将压缩传感理论与DFT算法相结合, 在无显著延长总观测时间的条件下, 改善了算法性能, 实现了对信号的精确测量, 为同步相量测量装置(Phasor measurement unit, PMU)的实现打下了良好基础。

1 相量测量基本原理

同步相量测量装置(Phasor measurement unit, PMU)是用于同步相量的测量与输出, 并进行动态数据记录的装置^{[10, 11]}。PMU的基本原理为:首先由GPS接收器输出1 PPS信号, 经过锁相振荡器后, 信号被划分成一定数量的脉冲用于采样, 再对信号进行滤波, 然后经数模(A/D)转换器量化, 最后按照离散傅里叶变换原理, 经微处理器计算出相量^[12]。PMU装置是电力系统实时动态监测的重要组成部分, 因此, 其必须具有较高的精确度和可靠性, 确保电力系统运行处于安全、稳定的状态, 同时保障数据测量的精度。PMU的典型结构如图1所示。

	Figure Option View Download New Window
	图1 PMU结构图Fig.1 Structure of PMU

在实际测量时, 电网频率总是在工频(50 Hz)附近波动, 使系统频率和采样频率不能同步, 造成非同步采样, 导致出现频谱泄露和栅栏效应, 影响系统测量精度。因此, 为消除或减小由于非同步采样造成的DFT测量误差, 本文提出了一种基于压缩传感的修正离散傅里叶变换的同步相量测量算法。

2 CS-DFT算法

2.1 压缩传感理论

压缩传感(Compressed sensing, CS)理论是由Donoho等^{[13, 14]}提出的一种新型的信息获取指导理论。该理论指出:对可压缩的信号可通过远低于奈奎斯特标准的方式进行数据采样, 仍能精确地恢复出原始信号。压缩传感的优点在于信号的投影测量数据量远远小于传统采样方法所获得数据量, 突破了奈奎斯特采样定理的瓶颈, 使得高分辨率信号的采集成为可能。

压缩传感理论主要包括3个方面:稀疏表示、编码测量和重构算法。图2为压缩传感理论的基本框架。

	Figure Option View Download New Window
	图2 压缩传感理论基本框架Fig.2 Basic framework of compressed sensing theory

下面从这3个方面对压缩传感理论进行分析:

设测量信号为x∈ R^n×¹, 其中n为信号长度, 对x进行压缩传感的过程如下。

(1)稀疏表示:信号的稀疏变换就是信号必须在某种变换下稀疏表示, 这是压缩传感的先验条件。设计过完备字典D= $\begin{matrix} \{D_{1}, D_{2}, \dots, D_{n}\} \end{matrix}$ , 使信号x在过完备字典上具有稀疏性, 即:

x=Da(1)

式中:a是稀疏变量。

(2)编码测量:在编码测量中最重要的一步是确定投影矩阵, 为了确保信号的线性投影能够保持信号的原始结构, 投影矩阵必须满足约束等距性(Restricted isometry property, RIP)条件。设观测矩阵为Φ ∈ R^{m× n} $\begin{matrix} (m ≪ n) \end{matrix}$ , 则测量向量为y=Φ x。

(3)信号重构:先运用重构算法由测量值及投影矩阵重构原始信号, 即从测量向量y中恢复出原始信号x, 然后利用重构算法求解最优问题min‖ x‖ , s.t.y=Φ x。

2.2 信号的建模

本文以信号的标准形式为出发点, 来表示不同特征的电力信号^[15]:

s(t)=Acos(\bar{w}t+φ )(2)

式中:\bar{w}为角频率; φ 为初相角; A为幅值, 其利用欧拉公式可以展开为:

s(t)= $\begin{matrix} \frac{A}{2} \end{matrix} \begin{matrix} \end{matrix}$ (3)

由于实际同步相量测量信号能够通过多个正弦波叠加的形式来表示, 因此可利用复指数形式表示为:

s(t)= $\begin{matrix} \sum_{h} \end{matrix} \begin{matrix} [\frac{A_{h}}{2} e^{j (φ_{h} + 2 π f_{h} t)} + \frac{A_{h}}{2} e^{- j (φ_{h} + 2 π f_{h} t)}] \end{matrix}$ (4)

式中:A_h为正弦信号的幅值; φ _h为相角; f_h为第h个波形分量的频率值, 且f_h=h· f₀, 其中f₀为基波频率, h为正弦波的个数; t为时间。

现给定长度为N的样本序列, 对其进行DFT算法处理, 可得到一组相应的N个频域系数, 即:

s $\begin{matrix} (\frac{k}{N}) \end{matrix}$ = $\begin{matrix} \sum_{h \in S_{H}} \end{matrix} \begin{matrix} \frac{A_{h}}{2} \end{matrix} \begin{matrix} e^{j φ_{h}} \end{matrix} \begin{matrix} \frac{sinN (\frac{k}{N} - f_{h} \cdot T_{s})}{Nsinπ (\frac{k}{N} - f_{h} \cdot T_{s})} \end{matrix}$ · $\begin{matrix} e^{- [jπ (\frac{k}{N} - f_{h} \cdot T_{s}) (N - 1) + j 2 π (\frac{k}{N} - f_{h} \cdot T_{s}) n_{0}]} \end{matrix}$ = $\begin{matrix} \sum_{h \in S_{H}} \end{matrix} \begin{matrix} \frac{A_{h}}{2} \end{matrix} \begin{matrix} e^{j φ_{h}} \end{matrix} \begin{matrix} \frac{sinN (\frac{k}{N} - f_{h} \cdot T_{s})}{Nsinπ (\frac{k}{N} - f_{h} \cdot T_{s})} \end{matrix}$ · $\begin{matrix} e^{- jπ (\frac{k}{N} - f_{h} \cdot T_{s}) (N - 1)} \end{matrix} \begin{matrix} e^{- j 2 π (\frac{k}{N} - f_{h} \cdot T_{s}) n_{0}} \end{matrix}$ = $\begin{matrix} \sum_{h \in S_{H}} \end{matrix} \begin{matrix} \frac{A_{h}}{2} \end{matrix} \begin{matrix} e^{j φ_{h}} \end{matrix}$ D_N $\begin{matrix} (\frac{k}{N} - v_{h}) \end{matrix} \begin{matrix} e^{- j 2 π (\frac{k}{N} - v_{h}) n_{0}} \end{matrix}$ (5)

式中:k为采样点数, 0≤ k< N; v_h为由采样频率1/T_s归一化的第h个波形分量的频率, 且v_h=f_h· T_s; 指数n₀为序列中第一个样本的时间位置; S_H是所有复指数项的集合; D_N(· )为狄利克雷函数, 其定义为:

D_N $\begin{matrix} (v) \end{matrix}$ = $\begin{matrix} \frac{sinπNv}{Nsinπv} \end{matrix}$ e^-j^{π (}^N-¹⁾^v(6)

式中:v为离散归一化频率。

2.3 算法实现

为提高同步相量测量算法的频率分辨率, 由频率分辨率的定义:

Δ f= $\begin{matrix} \frac{1}{N \cdot T} \end{matrix}$ (7)

可知, 首先引入插值因子P(P为一个大小合适的整数), 使N'=PN, 以此使算法具有高频率分辨率, 即:

Δ f'= $\begin{matrix} \frac{1}{PNT} \end{matrix}$ (8)

式中:N为采样点数; T为采样间隔。

由此, 同步相量测量信号的归一化频率为:

v_h= $\begin{matrix} \frac{l_{h} + δ_{h}^{'}}{N'} \end{matrix}$ = $\begin{matrix} \frac{l_{h} + δ_{h}^{'}}{P} \end{matrix}$ · $\begin{matrix} \frac{1}{N} \end{matrix}$ (9)

式中:当整数l_h∈ [0, 1, …, N-1]时, $\begin{matrix} |δ_{h}^{'}| \end{matrix}$ ≤ $\begin{matrix} \frac{1}{2} \end{matrix}$ , 可近似有:

$\begin{matrix} {\dot{v}}_{h} \end{matrix}$ = $\begin{matrix} \frac{l_{h}}{NP} \end{matrix}$ (10)

式中: $\begin{matrix} {\dot{v}}_{h} \end{matrix}$ 为v_h的估计值。

S_h为相应波形分量的整数子集, 当S_h⊂{0, 1, …, N'-1}时, 即对于参数h, l∈ S_h意味着l=l_h, 此时可用 $\begin{matrix} {\dot{v}}_{h} \end{matrix}$ 代替v_h, 则式(5)近似为:

s $\begin{matrix} (\frac{k}{N}) \end{matrix}$ ≈ $\begin{matrix} \sum_{\frac{l \in S_{h}}{0 \leq l \leq N'}} \end{matrix} \begin{matrix} \frac{A_{h}}{2} \end{matrix} \begin{matrix} e^{j φ_{h}} \end{matrix}$ D_N $\begin{matrix} (\frac{k}{N} - \frac{l}{N'}) \end{matrix}$ (11)

0≤ k< N

为了使同步相量的测量运算起来更加简单、直观, 可将式(8)写成更紧凑的矩阵形式:

s≈ Da(12)

式中:s为包含同步相量测量信号DFT系数的向量; D为N× N'维矩阵; a为包含同步相量测量信号的相量值的向量, 且由于a中大多数元素均为零, 因此, 可认为a具有稀疏性。

在实际测量测量中, 还需要考虑噪声等不定因素, 因此, 式(12)为:

X=s+n=Da+e(13)

式中:X为原始测量向量; e为噪声信号。

因此, 由上述分析可知, 可将该问题看作为压缩传感问题, 即考虑将CS方法与DFT算法相结合应用于同步相量测量中。其中, 用CS理论解求解(13)的表示如下:

$\begin{matrix} \{\begin{matrix} \dot{a} = \underset{a}{arg min} ‖ a ‖_{0} \\ subject to : ‖ X - Da ‖_{2} \leq ε \end{matrix} \end{matrix}$ (14)

式中:‖ a‖ ₀是l⁰的范数, 即a的非零元素的个数; ε 为给定的阈值。

接下来, 通过正交匹配追踪(Orthogonal matching pursuit, OMP)算法来恢复估计向量 $\begin{matrix} \dot{a} \end{matrix}$ , 其步骤如下:

步骤1 初始残余近似值r₀等于测量向量:r₀=X, 初始测量的索引集合设置为空: $\begin{matrix} {\dot{s}}_{0} \end{matrix}$ =∅。

引入矩阵 $\begin{matrix} D_{S_{t}} \end{matrix}$ , 其仅由以下算法步骤选择的D矩阵的列组成, 最初 $\begin{matrix} D_{S_{0}} \end{matrix}$ 有零列。该迭代计数器设置t=1。

步骤2 查找索引l_t, 使得:

l_t=arg $\begin{matrix} \max_{0 \leq l \leq N'} \end{matrix} \begin{matrix} {(D^{H} r_{t - 1})}_{2} \end{matrix}$ (15)

式中:上标H表示复共轭转置矩阵; r_t-₁为残差值; t为迭代次数。这一步迭代覆盖了该算法的索引恢复部分。

步骤3 增广估计索引集: $\begin{matrix} {\dot{S}}_{t} \end{matrix}$ = $\begin{matrix} {\dot{S}}_{t - 1} \end{matrix}$ ∪ $\begin{matrix} \{l_{t}\} \end{matrix}$ 。与矩阵D的列相对应的参数被附加到矩阵 $\begin{matrix} D_{S_{t}} \end{matrix}$ = $\begin{matrix} [D_{S_{t - 1}} d_{l_{t}}] \end{matrix}$ 中。

步骤4 计算一个新的向量:

$\begin{matrix} {\dot{a}}_{l_{t}} \end{matrix}$ =arg $\begin{matrix} \min_{a} \end{matrix} \begin{matrix} ‖ X - D_{S_{t}} a ‖_{2} \end{matrix}$ =( $\begin{matrix} D_{S_{t}}^{H} \end{matrix} \begin{matrix} D_{S_{t}} \end{matrix}$ )^-¹· $\begin{matrix} D_{S_{t}}^{H} \end{matrix}$ X(16)

式中:t是非零元素。这一步的迭代提供了逐步细化的估计。

步骤5 计算新的残差:r_t=X- $\begin{matrix} D_{S_{t}} \end{matrix} \begin{matrix} {\dot{a}}_{l_{t}} \end{matrix}$ , 然后增加迭代计数器:t=t+1, 判断是否满足t> k, 若满足, 则停止迭代; 若不满足, 则返回到步骤2。

此时, 得到向量 $\begin{matrix} \dot{a} \end{matrix}$ , 即同步相量测量信号的相量值, 利用稀疏矩阵, 由式(1)可得重构信号 $\begin{matrix} \dot{x} \end{matrix}$ =D $\begin{matrix} \dot{a} \end{matrix}$ 。

总的来说, CS-DFT算法是压缩传感与DFT算法的融合。首先利用离散傅里叶变换对测量信号进行稀疏化, 再通过狄利克雷函数来构造观测矩阵, 最后, OMP算法在稀疏矩阵约束范围内搜索最优的匹配原子, 提取特征信息, 最后重构出原测量信号, 为同步相量测量的进一步分析实验奠定了良好的基础。

3 仿真实验

3.1 测量信号模型

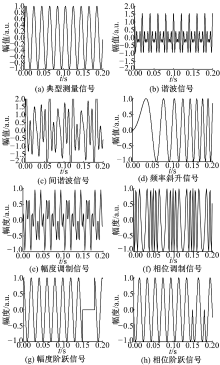
本文采用基波频率为50 Hz的同步相量测量信号, 信号采样点数为1024个, 采样频率为5.12 kHz, 时间为0.2 s, 对测量信号进行分析, 总结其基本特征, 构建典型测量信号的数学模型, 包括谐波和间谐波信号、频率斜升信号、幅度和相位调制信号, 以及幅度和相位阶跃信号, 如图3所示。

	Figure Option View Download New Window
	图3 测量信号模型Fig.3 Model of measurement sign

3.2 算法性能评价

目前, 衡量相量测量单元(PMU)性能的主要指标有两种:一是采用幅度误差和相位误差分别评价的方法; 二是采用综合矢量误差(Total vector error, TVE)来评价同步相量测量装置的测量误差^[15]。但由于TVE指标更为科学、全面, 可同时反映相量误差和幅度误差, 因此, 本文采用TVE评价方法。

TVE定义如下:

TVE= $\begin{matrix} \sqrt[]{\frac{{[X_{R} (n) - X_{R}]}^{2} + {[X_{I} (n) - X_{I}]}^{2}}{X_{R}^{2} + X_{I}^{2}}} \end{matrix}$

(17)

式中:X_R为理想信号相量的实部; X_I为理想信号相量的虚部; X_R(n)为实测相量的实部; X_I(n)为实测相量的虚部。

3.3 仿真实验及结果分析

利用本文方法对典型测量信号进行MATLAB仿真实验, 得到其DFT分析和CS-DFT分析。

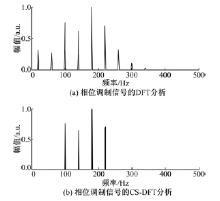
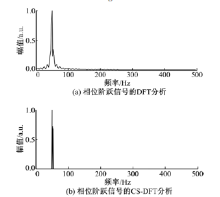
(1)在本次实验中, 以相位调制信号和相位阶跃信号为例, 其中, 相位调制信号的采样频率为5.12 kHz, 载波频率为100 Hz, 采样点数为1024个, 信号频率为40 Hz; 相位阶跃信号的采样频率为5.12 kHz, 采样点数为1024个, 信号频率为50 Hz, 实验对比结果分别如图4、图5所示。

	Figure Option View Download New Window
	图4 相位调制信号的DFT和CS-DFT分析Fig.4 DFT and CS-DFT analysis of phase modulation signal

	Figure Option View Download New Window
	图5 相位阶跃信号的DFT和CS-DFT分析Fig.5 DFT and CS-DFT analysis of phase step signal

由图4和图5可以看出, 本文CS-DFT方法能够有效地消除或减弱现有基于离散傅里叶变换的同步相量测量装置中普遍存在的频谱泄露和栅栏效应, 提高了相量测量的准确度, 减小了测量误差, 为WAMS系统打下了良好的基础, 为实现电力系统动态监测提供了可能。

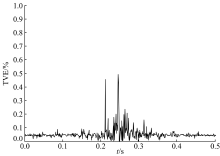
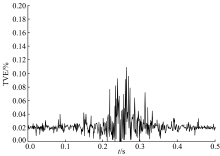
(2)在本次实验中, 分别用DFT和CS-DFT两种算法对信号进行相量测量, 得到各时刻的TVE值如图6、图7所示, 其中以相位调制信号为例, 时间为0.5 s, 采样点数为1024个, 采样频率为5.12 kHz。图6为在相位调制信号下的传统DFT算法的TVE值, 图7为在相位调制信号下的CS-DFT算法的TVE值。

	Figure Option View Download New Window
	图6 相位调制信号下DFT算法的TVE值Fig.6 TVE of DFT under phase modulation signal

	Figure Option View Download New Window
	图7 相位调制信号下CS-DFT算法的TVE值Fig.7 TVE of CS-DFT under phase modulation signal

由图6和图7可明显看出, DFT算法和CS-DFT算法的TVE值分别控制在0.6%和0.14%以下, TVE值均在合理范围内, 且CS-DFT算法的TVE值均小于DFT算法, 由此可证明两种算法均能满足相量测量的要求, CS-DFT算法的性能更优。

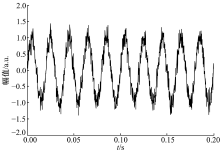
(3)为进一步证明CS-DFT算法的测量精度和通用性, 使测量结果更加准确, 在本次实验中, 以实际获取的工频测量信号为例, 如图8所示。

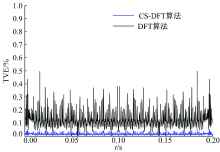
显而易见, 该工频测量信号含有干扰信号, 对其分别用DFT和CS-DFT两种算法进行分析实验, 得到各时刻的TVE值如图9所示。

	Figure Option View Download New Window
	图8 工频测量信号Fig.8 Power frequency measuring signal

	Figure Option View Download New Window
	图9 工频测量信号下DFT和CS-DFT算法的TVE值Fig.9 TVE of DFT and CS-DFT under power frequency measuring signal

由图9可明显看出, 在对不同测量信号进行MATLAB仿真实验时, CS-DFT算法的TVE值均小于DFT算法, 由此得出结论, CS-DFT算法指标优于DFT算法, CS-DFT算法对测量信号实现了精度更高的测量。

4 结束语

本文提出一种基于压缩传感理论的同步相量测量方法, 该方法可对测量信号的同步相量进行准确、有效的测量, 同时可明显消除或减小由于非同步采样造成的离散傅里叶变换的测量误差, 在很大程度上改善了传统DFT算法的测量精度, 能够满足WAMS系统的相关标准及要求, 为实现电力系统动态监测和安全稳定运行提供了有力的保障。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李建, 谢小荣, 韩英铎. 同步向量测量的若干关键问题[J]. 电力系统自动化, 2005, 29(1): 45-48. Li Jian, Xie Xiao-rong, Han Ying-duo. Key issues of the synchronized vector measurement[J]. Automation of Electric Power Systems, 2005, 29(1): 45-48. [本文引用:1]
[2]	吴京涛, 谢小荣, 王立鼎, 等. 广域测量系统在电力系统的发展与展望[J]. 电力设备, 2006, 7(3): 26-29. Wu Jing-tao, Xie Xiao-rong, Wang Li-ding, et al. Wide Area Measurement System Development and Prospect in the power system[J]. Electric Power Equipment, 2006, 7(3): 26-29. [本文引用:1]
[3]	Alasti H. Non-uniform-level crossing sampling for efficient sensing of temporally sparse signals[J]. Wireless Sensor Systems, 2014, 4(1): 27-34. [本文引用:1]
[4]	王茂海, 孙元章. 基于DFT的电力系统相量及功率测量新算法[J]. 电力系统自动化, 2005, 29(2): 20-24. Wang Mao-hai, Sun Yuan-zhang. A DFT-based method for phasor and power measurement in power systems[J]. Automation of Electric Power Systems, 2005, 29(2): 20-24. [本文引用:1]
[5]	周捷, 陈尧, 崔建中. 母线电压同步相角测量算法研究及实现[J]. 继电器, 2002, 30(3): 13-16. Zhou Jie, Chen Yao, Cui Jian-zhong. Study and implementation of the algorithm for bus synchronized voltage phase angle measurement[J]. Relay, 2002, 30(3): 13-16. [本文引用:1]
[6]	Kamwa I, Samantaray S R, Joos G. Compliance analysis of PMU algorithms and devices for wide-area stabilizing control of large power systems[J]. IEEE Trans on Power Systems, 2013, 28(2): 1766-1778. [本文引用:1]
[7]	汪芙平, 靳夏宁, 王赞基. 实现动态相量测量的FIR数字滤波器最优设计[J]. 中国电机工程学报, 2014, 34(15): 2388-2395. Wang Fu-ping, Jin Xia-ning, Wang Zan-ji. Optimal design of FIR digital filters for dynamic phasor measurement[J]. Proceedings of the CSEE, 2014, 34(15): 2388-2395. [本文引用:1]
[8]	徐建源, 王亮, 林莘, 等. 基于递推DFT同步相量测量算法的研究[J]. 高压电器, 2011, 47(11): 40-44. Xu Jian-yuan, Wang Liang, Lin Shen, et al. Based on recursive DFT phasor measurement algorithm[J]. High Voltage Apparatus, 2011, 47(11): 40-44. [本文引用:1]
[9]	丁涛, 董柏峰, 顾伟, 等. 基于PMU的电压稳定动态线性化指标优化切负荷算法[J]. 电力系统保护与控制, 2013, 41(9): 27-33. Ding Tao, Dong Bai-feng, Gu Wei, et al. Optimization of a load shedding scheme using dynamic voltage stability linearized index based on PMU[J]. Power System Protection and Control, 2013, 41(9): 27-33. [本文引用:1]
[10]	Faiz J, Lotfi-fard S, Shahri S H. Prony-based optimal bayes fault classification of overcurrent protection[J]. IEEE Transactions on Power Delivery, 2007, 22(3): 1326-1334. [本文引用:1]
[11]	Mai R K, He Z Y, Fu L, et al. A dynamic synchrophasor estimation algorithm for online application[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 570-578. [本文引用:1]
[12]	毕天姝, 刘灏, 杨奇逊. PMU 算法动态性能及其测试系统[J]. 电力系统自动化, 2014, 38(1): 62-67. Bi Tian-shun, Liu Hao, Yang Qi-xun. PMU algorithm and dynamic performance test system[J]. Automation of Electric Power Systems, 2014, 38(1): 62-67. [本文引用:1]
[13]	Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. [本文引用:1]
[14]	Donoho D L, Tsaig Y. Extensions of compressed sensing[J]. Signal Processing, 2006, 86(3): 533-548. [本文引用:1]
[15]	C37. 118—2005. IEEE stand ard for synchrophasors for power systems[S]. [本文引用:2]

2005

0.0

. 2005, 29(1):45-48 DOI:doi:10.3321/j.issn:1000-1026.2005.01.011

Key issues of the synchronized vector measurement

同步向量测量的若干关键问题

Li Jian , Xie Xiao-rong , Han Ying-duo.

李建, 谢小荣, 韩英铎

首先,阐述了非额定频率下相量的定义以及数据再同步对相量时标的要求.然后,结合数据再同步的需求分析了频率自适应采样方法在高密度的相量同步情况下的局限性;推导出一种在定间隔采样基础上能够有效消除非额定频率下离散傅里叶变换(DFT)算法产生的频率泄漏影响的相量校正算法.提出一种测试绝对相角测量精度的试验方法,并按照该方法验证了采用所提出的相量校正算法的相量测量单元(PMU)的相角测量精度.最后,通过仿真分析了基于DFT的相量算法的动态特性及其在暂态稳定控制中的适用范围.

... 0 引言广域测量系统(Wide area measurement system,WAMS)作为电网动态实时监测的新技术和重要手段,能实时地反映全网系统的动态变化,对电网的安全稳定运行起到了重要的作用^[1] ...

2006

0.0

. 2006, 7(3):26-29

Wide Area Measurement System Development and Prospect in the power system

广域测量系统在电力系统的发展与展望

Wu Jing-tao , Xie Xiao-rong , Wang Li-ding

吴京涛, 谢小荣, 王立鼎

... 而基于GPS技术的同步相量测量单元(Phasor measurement unit,PMU)正是WAMS系统的核心与基础^[2,3],并已被广泛应用在电网中以获得电网的实时动态变化,为实现电力系统动态监测提供了可能 ...

2014

0.0

2005

0.0

. 2005, 29(2):20-24 DOI:doi:10.3321/j.issn:1000-1026.2005.02.005

A DFT-based method for phasor and power measurement in power systems

基于DFT的电力系统相量及功率测量新算法

Wang Mao-hai , Sun Yuan-zhang.

王茂海, 孙元章

随着全球定位系统(GPS)的全面民用化以及通信技术的发展,电力系统实时相量测量技术日益受到关注.传统的基于离散傅里叶变换(DFT)的频率跟踪算法对相角误差的考虑不全面,从而其频率、相角、幅值等计算结果也不够准确.文中对DFT在非同步采样情况下的误差产生机理进行了全面分析,给出了非同步采样情况下DFT相角计算结果的精确误差表达式,基于该相角误差公式,提出了一种新的基于DFT的电力系统相量测量算法.与传统算法相比,该算法具有精确度高、可以自适应地抑制谐波干扰、计算量不大等优点,并用算例验证了这些优点.此外,还给出了实用的利用传统DFT方法计算功率的误差估计公式.

... 目前,国内外学者提出了多种同步相量测量算法,主要包括离散傅里叶变换(Discrete Fourier transform,DFT)法^[4]、过零点检测法(Zero crossing technique)^[5]和数字滤波器法^[6,7]等 ...

2002

0.0

. 2002, 30(3):13-16 DOI:doi:10.3969/j.issn.1674-3415.2002.03.004

Study and implementation of the algorithm for bus synchronized voltage phase angle measurement

母线电压同步相角测量算法研究及实现

Zhou Jie , Chen Yao , Cui Jian-zhong.

周捷, 陈尧, 崔建中

摘　要：讨论了基于GPS绝对时钟的电力系统母线电压同步相角测量的实现方法，研究了电压相角的过零测量法、离散Fourier和递归Fourier算法，探讨了变采样速率的同步相量测量算法。利用DSP数据处理芯片实现了基于DFT算法的GPS同步电压相角测量装置的软硬件设计，给出了实验仿真结果。

2013

0.0

2014

0.0

. 2014, 34(15):2388-2395

Optimal design of FIR digital filters for dynamic phasor measurement

实现动态相量测量的FIR数字滤波器最优设计

Wang Fu-ping , Jin Xia-ning , Wang Zan-ji.

汪芙平, 靳夏宁, 王赞基

2011

0.0

. 2011, 47(11):40-44

Based on recursive DFT phasor measurement algorithm

基于递推DFT同步相量测量算法的研究

Xu Jian-yuan , Wang Liang , Lin Shen

徐建源, 王亮, 林莘

为了减小测量误差,设计一种计算量小、采样精度高、可同时测量相角、频率和幅值的方法,笔者分析了同步相量的主要测量算法和现有同步相量测量方法。由传统的DFT算法引入计算量少的递推傅里叶算法,通过变换得到一种改进型递推离散傅里叶算法,并给出频率测量的方法,对同步向量测量进行误差分析,并提出改进措施和方案。实验由高精度和可调节的信号源作为相量采集装置的输入量,实验结果表明,基于递推DFT同步相量测量算法正确。

... 但在非同步采样的情况下,现有的DFT算法往往会在幅值和频率测量上出现误差,且误差会随着非同步性的增强而急剧增大,导致出现频谱泄露和栅栏效应,使温测量结果达不到实际应用的要求^[8] ...

2013

0.0

. 2013, 41(9):27-33

Optimization of a load shedding scheme using dynamic voltage stability linearized index based on PMU

基于PMU的电压稳定动态线性化指标优化切负荷算法

Ding Tao , Dong Bai-feng , Gu Wei

丁涛, 董柏峰, 顾伟

紧急状况下,优化包含动态负荷的系统切负荷量,以保证系统电压快速恢复正常状态是系统安全的关键.利用PMU测量信息推导了电压稳定动态线性化指标的灵敏度,将其作为实施切负荷的作用因子.建立了以切负荷量最小为目标函数和电压指标偏差量为约束条件的切负荷优化模型.首次实现了分区多步切负荷的算法,在实时计算得到的动态电压稳定指标超标基础上,利用所提出的优化模型实施多步动态优化切负荷,并实时修正作用因子的灵敏度,克服了传统一步欠切或过切的缺点. 用IEEE14节点测试系统和国内实际电网算例证实了该方法的可行性和有效性.

... 同步相量的不准确测量最终将导致电网的动态安全监控能力下降,严重时将影响电网的安全稳定运行^[9] ...

2007

0.0

... 1 相量测量基本原理同步相量测量装置(Phasor measurement unit,PMU)是用于同步相量的测量与输出,并进行动态数据记录的装置^[10,11] ...

2010

0.0

... 1 相量测量基本原理同步相量测量装置(Phasor measurement unit,PMU)是用于同步相量的测量与输出,并进行动态数据记录的装置^[10,11] ...

2014

0.0

. 2014, 38(1):62-67 DOI:doi:10.7500/AEPS20130410001

PMU algorithm and dynamic performance test system

PMU 算法动态性能及其测试系统

Bi Tian-shun , Liu Hao , Yang Qi-xun.

毕天姝, 刘灏, 杨奇逊

摘　要：同步相量测量单元（PMU）的量测性能,特别是动态条件下的量测精度,是其能否更好地服务于电力系统动态过程监测、分析与控制应用的基础。在简述PMU离散傅里叶变换（DFT）算法的基础上,重点利用相量因子的概念,分析了相量算法的动态特性,揭示了其在计算动态相量时出现的平均化效应;进一步给出了即使在相量计算平均化效应的情况下,通过改变时标位置减小动态相量计算误差的理论分析。文中采用实际PMU实验数据验证了上述理论分析的正确性。此外,为了能够系统、客观地评价PMU的动态性能,设计了PMU静、动态自动测试系统,可为PMU动态性能评估提供支撑。

... PMU的基本原理为:首先由GPS接收器输出1 PPS信号,经过锁相振荡器后,信号被划分成一定数量的脉冲用于采样,再对信号进行滤波,然后经数模(A/D)转换器量化,最后按照离散傅里叶变换原理,经微处理器计算出相量^[12] ...

2006

0.0

... 1 压缩传感理论压缩传感(Compressed sensing,CS)理论是由Donoho等^[13,14]提出的一种新型的信息获取指导理论 ...

2006

0.0

... 1 压缩传感理论压缩传感(Compressed sensing,CS)理论是由Donoho等^[13,14]提出的一种新型的信息获取指导理论 ...

0.0

... 2 信号的建模本文以信号的标准形式为出发点,来表示不同特征的电力信号^[15]: ...

... 二是采用综合矢量误差(Total vector error,TVE)来评价同步相量测量装置的测量误差^[15] ...