信号交叉口自行车和行人混合交通流社会力模型

引用本文

王占中, 赵利英, 焦玉玲, 曹宁博. 信号交叉口自行车和行人混合交通流社会力模型[J].吉林大学学报（工学版）, 2018,48(1): 89-97
WANG Zhan-zhong, ZHAO Li-ying, JIAO Yu-Ling, CAO Ning-bo. Social force model of pedestrian-bike mixed flow at signalized crosswalk[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 89-97 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161255
Permissions

信号交叉口自行车和行人混合交通流社会力模型

王占中, 赵利英, 焦玉玲, 曹宁博

吉林大学交通学院,长春 130022

通讯作者：焦玉玲(1968-),女,副教授.研究方向:物流系统设施设备规划与设计.E-mail:jyling777@163.com

作者简介:王占中(1965-),男,教授,博士生导师.研究方向:运输资源优化技术.E-mail:wangzz@jlu.edu.cn

基金:国家自然科学基金项目(51578262)

摘要

基于行人仿真的社会力模型,考虑自行车对行人过街的干扰,引入自行车与行人以及自行车与人行横道间的相互作用,提出了一种改进的自行车和行人混合交通流的社会力模型。通过数值模拟,分析了自行车道的设置对混合交通流事故数及到达率的影响,再现了自行车和行人混合交通流中自行车的跟随和分层现象。仿真结果表明:设置自行车道能够有效缓解行人和自行车之间的冲突,有助于减少行人和自行车的事故数并提高混合交通流的运行效率;根据自行车数量,设置合理的自行车道,能够保证自行车达到最大过街速度,从而提高自行车的过街效率;模型能够重现混合交通流的自组织等现象。

关键词: 交通运输系统工程; 社会力模型; 自行车; 行人; 混合交通

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2018)01-0089-09

Social force model of pedestrian-bike mixed flow at signalized crosswalk

WANG Zhan-zhong, ZHAO Li-ying, JIAO Yu-Ling, CAO Ning-bo

College of Transportation, Jilin University, Changchun, 130022, China

Abstract

Based on basic social force model, considering the interference of bikes on pedestrian, this paper presents a modified social force model to describe the interactions between bikes and pedestrians. By simulation, the influences of the setting cyclists' path on the number of pedestrians and bicycle accidents and the arrival rate of bicycles were analyzed; and then, the slipstreaming, self-organization and lane-forming of bicycle and pedestrian mixed flow were reproduced, which obeys the observed data. The simulation results show that setting of cyclists' path can effectively alleviate the conflicts of bicycles and pedestrians, and help to reduce the number of potential traffic accidents of pedestrian and bicycle mixed flow, thus, improving the operation efficiency of the mixed traffic flow. Comparison of the simulation results and the observed data proves the effectiveness of the modified model. Besides, conclusions are drawn that with the increase of bicycle traffic, setting the cyclists' path on the crosswalk becomes more beneficial. Furthermore, setting wider cyclists' path according to the bicycle volume can guarantee bicycles to cross the crosswalk with maximum speed. The simulation model enables us to visually represent pedestrian and cyclist collective phenomenon.

Keyword: engineering of communications and transportation system; social force model; bike; pedestrian; mixed traffic flow

Show Figures

0 引言

在中国, 自行车出行非常普遍。自行车通常与行人共用人行横道, 但因为自行车与行人的相互干扰, 共享人行横道不仅会降低行人的运行效率, 而且会威胁行人安全。因此, 许多国家采取了相应措施来缓解这一状况, 其中, 日本在人行横道旁设置单独自行车道, 将行人与自行车完全分离, 这一定程度上降低了自行车与行人的相互干扰, 但这种设计方法的安全性和有效性并未得到有效验证。目前, 尽管存在成熟的仿真工具服务于传统道路设计, 但研究共享空间的仿真模型却并不多见。对行人和自行车运动机制建模对道路行人设施的安全性评价和人行横道的通行能力评估都有至关重要的作用^[1]。因此本文利用社会力模型对自行车与行人的运行机制进行建模, 分析了自行车与行人分离设施的安全性和有效性。

行人能根据交通环境评估当前行为, 并调整下一时刻的行为, 移动过程中避免与其他行人和障碍物发生接触。基于此, Helbing等^[2]在1995年构建了用于模拟行人在空间运动的社会力模型, 该模型将行人与外界的相互作用量化为斥力和引力, 最初社会力模型只建立了行人与行人以及行人与障碍物间的作用力; 2000年Helbing等^[3]考虑行人的随机波动特性对模型的参数进行了修正; 2002年Helbing等^[4]在基本社会力模型的基础上, 引入了行人的空间需求特性, 考虑在拥挤条件下行人对其他行人的排斥力以及相互躲避的切向滑动力; 2005年Helbing等^[5]认为行人期望速度的变化仅由自驱力决定, 而实际中, 周围行人的速度也影响着行人的期望速度, 如果周围行人速度很快, 行人期望速度也会改变。在Helbing等^{[2, 3, 4, 5]}的研究基础上, Apel^[6]、Johansson^[7]完善了行人自驱力方向权重方程, 引入一个大于0且小于1的各向异性系数来反映行人对周围行人的影响强弱; Moussaid等^[8]通过对行人实际运动数据的分析发现, 两个行人运动方向的夹角和他们之间的距离严重影响着行人速度的变化, 通过数据拟合, 建立了行人运动转角大小与行人运动方向夹角及行人间距的经验模型。社会力模型在仿真大型场所行人疏散方面应用广泛, 并且形成了较为完整的仿真体系, 相关系数也已经过许多研究人员的完善, 然而, 利用社会力模型模拟路段或者信号交叉口处的行人过街行为并不多见, 涉及自行车的行人过街仿真更加少见。Zeng等^[9]构建了人行通道上的改进社会力模型, 分析得出行人的转角和速度大小改变都服从正态分布, 模型考虑了机动车以及信号灯对行人过街的影响, 并建立了相关的社会力模型方程。自行车微观仿真建模有助于理解自行车与行人相互干扰机制和评价自行车道设施安全性。

本文尝试对信号交叉口自行车与行人的混合交通进行建模仿真。作为连续空间模型, 社会力模型允许行人连续运动。因此本文在社会力模型的基础上, 引入自行车道对自行车和行人的作用力以及自行车的跟随力, 建立了自行车和行人混合交通流仿真的社会力模型。

1 基本社会力模型

基本社会力模型包括3个基本力:自驱力、个体之间相互作用力和个体与障碍物间的作用力, 在这些力的合力作用下, 个体(自行车和行人)产生加速度, 并时刻调整自己速度大小和方向, 以此向目的地移动。文中U=α 或U=β 为行人; U=i或U=j为自行车。

$\begin{matrix} {\vec{f}}_{U} \end{matrix}$ (t)= $\begin{matrix} {\vec{f}}_{U}^{0} \end{matrix}$ (t)+ $\begin{matrix} \sum_{U} \end{matrix} \begin{matrix} {\vec{f}}_{U_{1} U_{2}} \end{matrix}$ + $\begin{matrix} \sum_{B} \end{matrix} \begin{matrix} {\vec{f}}_{UB} \end{matrix}$ (1)

式中: $\begin{matrix} {\vec{f}}_{U} \end{matrix}$ (t)为个体U在t时刻受到的合力; $\begin{matrix} {\vec{f}}_{U}^{0} \end{matrix}$ (t)为个体U在t时刻的自驱力; $\begin{matrix} {\vec{f}}_{U_{1} U_{2}} \end{matrix}$ 为个体U₁和个体U₂之间的作用力; $\begin{matrix} {\vec{f}}_{UB} \end{matrix}$ 为障碍物对U的作用力。

1.1 自驱力

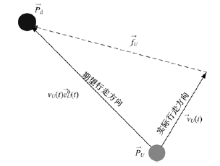
个体在自身主观意识作用下, 朝着期望位置移动, 因此自驱力可以看作是个体对自己施加的力。个体从期望速度完成减速需要一个基本的反应时间τ _U。在过街过程中, 个体根据周围环境调整速度方向和大小, 以保证最短路径过街。个体期望速度的方向为:

$\begin{matrix} {\vec{e}}_{U}^{0} \end{matrix}$ (t)= $\begin{matrix} \frac{{\vec{p}}_{d} - {\vec{p}}_{U}}{|{\vec{p}}_{d} - {\vec{p}}_{U}|} \end{matrix}$ (2)

式中: $\begin{matrix} {\vec{e}}_{U}^{0} \end{matrix}$ (t)为个体U在t时刻的期望速度方向; $\begin{matrix} {\vec{p}}_{d} \end{matrix}$ 为个体U的期望目的地; $\begin{matrix} {\vec{p}}_{U} \end{matrix}$ 为个体U在t时刻的实际位置。

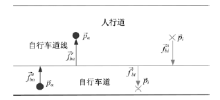
自驱力给个体一个作用力, 在反应时间内, 将个体从当前速度方向调整到期望速度方向, 如图1所示, 自驱力如式(3)所示。

$\begin{matrix} {\vec{f}}_{U}^{0} \end{matrix}$ ( $\begin{matrix} {\vec{v}}_{U} \end{matrix}$ )=m_U $\begin{matrix} \frac{v_{U}^{0} (t) {\vec{e}}_{U}^{0} (t) - {\vec{v}}_{U} (t)}{τ_{U}} \end{matrix}$ (3)

式中: $\begin{matrix} v_{U}^{0} \end{matrix}$ (t)为个体U在t时刻的期望速度大小; $\begin{matrix} {\vec{v}}_{U} \end{matrix}$ (t)为个体U在t时刻的实际行走速度; τ _U为个体U的反应时间; m_U为行人或自行车的质量, 仿真中行人质量设为1, 自行车质量设为2。

	Figure Option View Download New Window
	图1 期望速度和自驱力Fig.1 Expected speed and drive force

1.2 个体之间的作用力

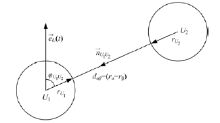
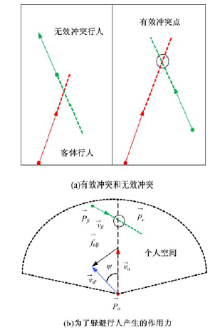
个体为自身的舒适和安全会保持一个隐私空间, 其他个体不能侵犯这个空间; 但是, 个体会受到其他个体影响, 当接近周围个体时, 其他个体就会对它产生作用力。随着群体密度的增大, 个体对空间的需求就会降低, 甚至出现相互接触的行为, 由此个体之间会产生一个接触力。由此可知, 个体之间作用力包含心理排斥力和物理力两部分, 如式(4)所示。个体质心之间距离如图2所示。

	Figure Option View Download New Window
	图2 个体间距离Fig.2 Distance between individuals

$\begin{matrix} {\vec{f}}_{U_{1} U_{2}} \end{matrix}$ (t)= $\begin{matrix} A_{U_{1}}^{1} \end{matrix}$ exp $\begin{matrix} [\frac{(r_{αβ} - d_{αβ})}{B_{U_{1}}^{1}}] \end{matrix} \begin{matrix} {\vec{n}}_{U_{1} U_{2}} \end{matrix} \begin{matrix} F_{U_{1} U_{2}} \end{matrix}$ +

Kg( $\begin{matrix} r_{U_{1} U_{2}} \end{matrix}$ - $\begin{matrix} d_{U_{1} U_{2}} \end{matrix}$ ) $\begin{matrix} {\vec{n}}_{U_{1} U_{2}} \end{matrix}$ +

kg( $\begin{matrix} r_{U_{1} U_{2}} \end{matrix}$ - $\begin{matrix} d_{U_{1} U_{2}} \end{matrix}$ )Δ $\begin{matrix} v_{U_{1} U_{2}}^{t} \end{matrix} \begin{matrix} t_{U_{1} U_{2}} \end{matrix}$ (4)

g(x)= $\begin{matrix} \{\begin{matrix} x, x > 0 \\ 0, 其他 \end{matrix} \end{matrix}$ (5)

式中: $\begin{matrix} A_{U_{1}}^{1} \end{matrix}$ 为作用力强度; $\begin{matrix} B_{U_{1}}^{1} \end{matrix}$ 为作用力范围; $\begin{matrix} d_{U_{1} U_{2}} \end{matrix}$ 是个体质心之间距离; $\begin{matrix} r_{U_{1} U_{2}} \end{matrix}$ 是个体半径的和; $\begin{matrix} {\vec{n}}_{U_{1} U_{2}} \end{matrix}$ 为个体U₂指向个体U₁的向量, 如式(6)所示; $\begin{matrix} t_{U_{1} U_{2}} \end{matrix}$ 为个体之间切线方向; Δ $\begin{matrix} v_{U_{1} U_{2}}^{t} \end{matrix}$ 为切线方向速率差; K和k是很大的常数; $\begin{matrix} F_{U_{1} U_{2}} \end{matrix}$ 是个体各向异性特性, 如式(7)所示。 $\begin{matrix} F_{U_{1} U_{2}} \end{matrix}$ 为个体U₁前方个体对他的影响比后方个体大。

$\begin{matrix} {\vec{n}}_{U_{1} U_{2}} \end{matrix}$ = $\begin{matrix} \frac{{\vec{p}}_{U_{1}} - {\vec{p}}_{U_{2}}}{d_{U_{1} U_{2}} (t)} \end{matrix}$ (6)

式中: $\begin{matrix} {\vec{p}}_{U_{1}} \end{matrix}$ 是个体U₁的位置; $\begin{matrix} {\vec{p}}_{U_{2}} \end{matrix}$ 是个体U₂的位置。

$\begin{matrix} F_{U_{1} U_{2}} \end{matrix}$ =λ _α+(1-λ _α) $\begin{matrix} \frac{1 + \cos (φ_{U_{1} U_{2}})}{2} \end{matrix}$ (7)

式中:λ _α体现行人运动的各向异性, 且0≤ λ _α≤ 1; $\begin{matrix} φ_{U_{1} U_{2}} \end{matrix}$ 为个体U₁和U₂运动方向的夹角;

cos( $\begin{matrix} φ_{U_{1} U_{2}} \end{matrix}$ )=- $\begin{matrix} {\vec{n}}_{U_{1} U_{2}} \end{matrix} \begin{matrix} {\vec{e}}_{U_{1}} \end{matrix}$ (t)(8)

$\begin{matrix} {\vec{e}}_{U_{1}} \end{matrix}$ (t)= $\begin{matrix} \frac{{\vec{v}}_{U_{1}} (t)}{|{\vec{v}}_{U_{1}} (t)|} \end{matrix}$ (9)

1.3 障碍物的作用力

个体通常会与障碍物保持一定的距离, 参照个体之间作用力的表达式, 个体与障碍的作用力可用下式表达:

$\begin{matrix} {\vec{f}}_{UB} \end{matrix}$ =A_UBexp $\begin{matrix} [\frac{(r_{UB} - d_{UB})}{B_{UB}}] \end{matrix} \begin{matrix} {\vec{n}}_{UB} \end{matrix}$ (10)

式中: $\begin{matrix} {\vec{f}}_{UB} \end{matrix}$ 是障碍物对个体U的作用力; A_UB为障碍物作用力强度; B_UB为障碍物作用力范围; d_UB是个体到障碍物的距离; r_UB为半径和; $\begin{matrix} {\vec{n}}_{UB} \end{matrix}$ 为由边界指向个体U的向量。

2 社会力模型修正

2.1 行人到达位置与期望位置分布

行人根据期望位置, 实时调整当前速度方向, 选择距离期望位置最近的轨迹过街。以往研究中, 期望位置是随机的, 本文行人期望位置分布采用Zeng等^[9]建立的行人期望位置的分布模型, 即利用韦布尔分布构建了如下行人期望位置的分布模型:

f(x, a, b)= $\begin{matrix} \frac{a}{b} \end{matrix} \begin{matrix} {(\frac{x}{b})}^{a - 1} \end{matrix} \begin{matrix} e^{- {(\frac{x}{b})}^{a}} \end{matrix}$ (11)

式中:f(x, a, b)为韦布尔分布的概率密度; a为形状参数; b为尺度参数。

建立a、b与人行横道宽度、行人密度、行人起始和目的地位置的函数关系, 如式(12)和(13)所示:

a=λ _{1, 0}+λ _{1, 1}y_{1, 1}+λ _{1, 2}y_{1, 2}+λ _{1, 3}y_{1, 3}(12)

b=λ _{2, 0}+λ _{2, 1}y_{1, 1}+λ _{2, 2}y_{1, 2}+λ _{2, 3}y_{1, 3}(13)

式中:y_{1, 1}、y_{1, 2}、y_{1, 3}为人行横道宽度、行人密度、行人起始和目的地位置; λ _{1, 0}、λ _{1, 1}、λ _{1, 2}、λ _{1, 3}和λ _{2, 0}、λ _{2, 1}、λ _{2, 2}、λ _{2, 3}为模型系数。

2.2 自行车与行人的相互作用力

本文类比行人与行人的相互作用, 自行车被看作具有一定半径的圆形实体, 自行车与行人的相互作用力也由心理力和物理力组成。当行人遇到自行车时, 自行车就会对行人产生排斥力以保证自行车的安全行驶空间; 当行人和自行车密度很大时, 行人可能会与自行车接触, 即自行车与行人发生碰撞, 此时自行车会对行人产生一个接触力, 如式(14)表示:

$\begin{matrix} \begin{matrix} {\vec{f}}_{α i} (t) = A_{α i} \exp [\frac{(r_{α i} - d_{α i})}{B_{α i}}] {\vec{n}}_{α i} F_{α i} + \\ Kg (r_{α i} - d_{α i}) {\vec{n}}_{α i} + kg (r_{α i} - d_{α i}) Δ v_{α i}^{t} t_{α i} \end{matrix} \end{matrix}$ (14)

式中: $\begin{matrix} {\vec{f}}_{αi} \end{matrix}$ 为自行车i对行人α 的作用力; A_α_i为作用力强度; B_α_i为作用力范围; r_α_i是半径和; d_α_i是自行车与行人质心之间距离。

2.3 自行车之间的跟随力与排斥力

实际自行车过街时, 如果前方存在其他自行车, 后方自行车为减小过街阻力, 就会跟随着前方自行车移动, 而当后方自行车特别靠近前方自行车时, 为了自身的安全, 后方自行车又会减速行驶, 这就是常见的跟随现象。为反映这种常见现象, 本文建立了前方自行车对后方自行车的作用力模型。如图3所示, 前方自行车对后方自行车的作用力可以这样描述:当两辆自行车之间的距离ε ₂≤ d≤ ε ₁时, 后方自行车会加速, 以达到跟随前车过街的目的; 当两辆自行车之间距离过大或者过小时, 这种跟随行为消失。因跟随力只在ε ₂≤ d≤ ε ₁时起作用, 当后方自行车超车时, 会选择从远离前方自行车的位置完成超车, 超车时自行车之间的相互作用力不包含跟随力。自行车之间的这种跟随力可以用式(15)表示。

	Figure Option View Download New Window
	图3 自行车跟随力Fig.3 Bike following force

$\begin{matrix} {\vec{f}}_{ij}^{following} \end{matrix}$ = $\begin{matrix} \{\begin{matrix} A_{ij}^{f} \exp [\frac{({\vec{r}}_{ij} - {\vec{d}}_{ij})}{B_{ij}^{f}}] {\vec{e}}_{ij} F_{ij}, ε_{2} \leq d_{ij} \leq ε_{1} \\ 0, 其他 \end{matrix} \end{matrix}$ (15)

式中: $\begin{matrix} {\vec{f}}_{ij}^{following} \end{matrix}$ 为自行车i与自行车j之间的跟随力; $\begin{matrix} A_{ij}^{f} \end{matrix}$ 为作用力强度; $\begin{matrix} B_{ij}^{f} \end{matrix}$ 为作用力范围; $\begin{matrix} {\vec{r}}_{ij} \end{matrix}$ 为半径和; $\begin{matrix} {\vec{e}}_{ij} \end{matrix}$ 为i指向j的单位向量; ε ₁、ε ₂为常数。相似于F_{α β}, 引入各向异性系数F_ij如下:

F_ij= $\begin{matrix} (λ_{α} + (1 - λ_{α}) \frac{1 + \cos (φ_{ij})}{2}) \end{matrix}$ p₁(16)

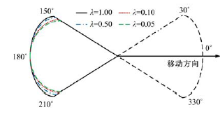
式中:F_ij表示前方自行车只对后方自行车产生跟随力, 对前方自行车没有影响。F_ij的大小随着λ _α的变化而变化, 如图4所示。

	Figure Option View Download New Window
	图4 各向异性系数示意图Fig.4 Anisotropic factor diagram

p是调整系数, 可以用来确定跟随力的大小和影响范围, p可以用式(17)计算得到:

p= $\begin{matrix} \{\begin{matrix} 1, 150 ° \leq φ_{ij} \leq 210 ° \\ 0, 其他 \end{matrix} \end{matrix}$ (17)

2.4 自行车道对行人和自行车的作用力

自行车道将行人和自行车分离。通常情况下, 行人遵守交通规则在人行横道内行走, 行人会与自行车道和人行横道边界保持安全距离。这意味着, 当行人位于人行道内部时, 自行车道和人行横道边界对行人有排斥作用, 使行人持续在人行横道内行走。而当行人因为拥挤或者偶然因素进入自行车道后, 行人在后续的运动过程中会逐步返回人行道内行走, 这说明自行车道产生一个引力, 将行人拉回人行横道。行人和自行车的受力如图5所示。

	Figure Option View Download New Window
	图5 自行车道对行人和自行车的作用力示意图Fig.5 Reaction among cyclist path, pedestrian and cyclists

同样的, 自行车道在自行车道内时, 自行车道对自行车产生一个斥力, 使自行车持续在自行车道内行走; 反之, 自行车受到边界对它的引力, 进而回到自行车道。类似于边界对行人的作用力, 用分段函数表示自行车道对行人和自行车的作用力, 如式(18)和(19)所示:

$\begin{matrix} {\vec{f}}_{bα} \end{matrix}$ = $\begin{matrix} \{\begin{matrix} A_{bα}^{r} \exp (\frac{| p_{α} - p_{b} |}{B_{bα}^{r}}) {\vec{n}}_{bα}, \\ 在人行道内 \\ A_{bα}^{a} \exp (\frac{| p_{α} - p_{b} |}{B_{bα}^{a}}) (- {\vec{n}}_{bα}), \\ 在自行车道内 \end{matrix} \end{matrix}$ (18)

式中: $\begin{matrix} {\vec{f}}_{bα} \end{matrix}$ 为自行车道线对行人α 的作用力; $\begin{matrix} A_{bα}^{r} \end{matrix}$ 与 $\begin{matrix} A_{bα}^{a} \end{matrix}$ 为作用力强度; $\begin{matrix} B_{bα}^{r} \end{matrix}$ 与 $\begin{matrix} B_{bα}^{a} \end{matrix}$ 为作用力范围; p_α为行人α 位置; p_b为自行车道位置; $\begin{matrix} {\vec{n}}_{bα} \end{matrix}$ 为自行车道指向行人α 的向量。

$\begin{matrix} {\vec{f}}_{bi} \end{matrix}$ = $\begin{matrix} \{\begin{matrix} A_{bi}^{r} \exp (\frac{| p_{i} - p_{b} |}{B_{bi}^{r}}) {\vec{n}}_{bi}, \\ 在自行车道内 \\ A_{bi}^{a} \exp (\frac{| p_{i} - p_{b} |}{B_{bi}^{a}}) (- {\vec{n}}_{bi}), \\ 在人行道内 \end{matrix} \end{matrix}$ (19)

式中: $\begin{matrix} {\vec{f}}_{bi} \end{matrix}$ 为自行车道对自行车i的作用力; $\begin{matrix} A_{bi}^{r} \end{matrix}$ 与 $\begin{matrix} A_{bi}^{a} \end{matrix}$ 为作用力强度; $\begin{matrix} B_{bi}^{r} \end{matrix}$ 与 $\begin{matrix} B_{bi}^{a} \end{matrix}$ 为作用力范围; p_i为行人i位置; p_b为自行车道位置; $\begin{matrix} {\vec{n}}_{bi} \end{matrix}$ 为自行车道指向自行车i的法向量。

2.5 行人冲突避让机制

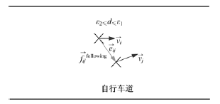
当行人(自行车)与其他行人(自行车)将要发生冲突时, 行人(自行车)会采取减速或者停止来避免冲突。准确的冲突避让模型能够有效降低仿真中出现的行(自行车)重叠现象。常见的冲突可以分为两类, 如图6(a)所示。然而, 并非所有的冲突都会转变成碰撞(即事故), 因此应该建立准确的模型判别冲突是否有效。

	Figure Option View Download New Window
	图6 行人(自行车)避免冲突产生的作用力Fig.6 Force of pedestrians (bikes) avoiding conflict

TC表示行人(自行车)以下个仿真步长的速度到达冲突点所需要的时间, TC_α和TC_β分别表示行人(自行车i)α 和行人(自行车j)β 到达冲突点所需要的时间。利用式(20)(21)可以计算得到TC_α和TC_β。

TC_α= $\begin{matrix} \frac{‖ {\vec{P}}_{c} - {\vec{P}}_{α} ‖}{‖ {\vec{v}}_{α}^{next} ‖} \end{matrix}$ cos< $\begin{matrix} {\vec{P}}_{c} \end{matrix}$ - $\begin{matrix} {\vec{P}}_{α} \end{matrix}$ , $\begin{matrix} {\vec{v}}_{α}^{next} \end{matrix}$ > (20)

TC_β= $\begin{matrix} \frac{‖ {\vec{P}}_{c} - {\vec{P}}_{β} ‖}{‖ {\vec{v}}_{β}^{next} ‖} \end{matrix}$ cos< $\begin{matrix} {\vec{P}}_{c} \end{matrix}$ - $\begin{matrix} {\vec{P}}_{β} \end{matrix}$ , $\begin{matrix} {\vec{v}}_{β}^{next} \end{matrix}$ > (21)

式中: $\begin{matrix} {\vec{P}}_{α} \end{matrix}$ 表示行人α 的当前位置; $\begin{matrix} {\vec{P}}_{β} \end{matrix}$ 是行人β 当前的位置; $\begin{matrix} {\vec{P}}_{c} \end{matrix}$ 是冲突点的位置。

首先, 根据行人(自行车)α 和β 当前的速度 $\begin{matrix} {\vec{v}}_{α} \end{matrix}$ 和 $\begin{matrix} {\vec{v}}_{β} \end{matrix}$ 计算出在下个仿真步长的速度 $\begin{matrix} {\vec{v}}_{α}^{next} \end{matrix}$ 和 $\begin{matrix} {\vec{v}}_{β}^{next} \end{matrix}$ , 如式(22)(23)所示:

$\begin{matrix} {\vec{v}}_{α}^{next} \end{matrix}$ = $\begin{matrix} {\vec{v}}_{α} \end{matrix}$ + $\begin{matrix} {\vec{f}}_{α} \end{matrix}$ (t)Δ t/m_α(22)

$\begin{matrix} {\vec{v}}_{β}^{next} \end{matrix}$ = $\begin{matrix} {\vec{v}}_{β} \end{matrix}$ + $\begin{matrix} {\vec{f}}_{β} \end{matrix}$ (t)Δ t/m_β(23)

只有当TC_α和TC_β均大于0, 行人(自行车)α 和行人(自行车)β 之间的冲突才是有效的。其他条件下, 行人(自行车)或者已经通过冲突点, 或者不存在潜在的冲突。

如式(24)所示, TC_{α β}是TC_α和TC_β差的绝对值。TC_{α β}可以用来表示行人(自行车)α 和β 之间的冲突风险。TC_{α β}越大表示冲突风险越小。

TC_{α β}= $\begin{matrix} \{\begin{matrix} |T C_{α} - T C_{β}|, T C_{α} > 0 andT C_{β} > 0 \\ + \infty, 其他 \end{matrix} \end{matrix}$ (24)

当冲突被判定有效时, 行人(自行车)α 将会采取避让措施来避免与行人(自行车)β 的冲突。行人(自行车)α 通过调整速度大小和方向来实现避免冲突的目的。冲突避让的流程图如图7所示。

	Figure Option View Download New Window
	图7 冲突避让流程图Fig.7 Flow chart of individual collision avoidance

调整后的速度 $\begin{matrix} {\vec{v}}_{α}^{*} \end{matrix}$ 如式(25)所示:

$\begin{matrix} {\vec{v}}_{α}^{*} \end{matrix}$ =(1+Δ v) $\begin{matrix} {\vec{v}}_{α} \end{matrix}$ ω (ψ )(25)

ω (ψ )= $\begin{matrix} [\begin{matrix} cosψ & - & sinψ \\ sinψ & cosψ \end{matrix}] \end{matrix}$ (26)

式中:ψ 为逆时针偏移角度; Δ v为速度的变化量。

因此, 为避让行人(自行车)而产生的躲避力 $\begin{matrix} {\vec{f}}_{αβ}^{r} \end{matrix}$ 可以表示为:

$\begin{matrix} {\vec{f}}_{αβ}^{r} \end{matrix}$ = $\begin{matrix} \frac{{\vec{v}}_{α}^{*} - {\vec{v}}_{α}}{Δt} \end{matrix}$ (27)

3 仿真模拟与分析

本文对自行车和行人混合交通流进行了仿真。对比常规人行横道, 混行交通流中存在更多的相互作用与冲突, 设置自行车道后, 行人和自行车的相互作用减少。然而, 自行车道的设置能否降低这种相互作用?如果能降低, 自行车道又该如何根据交通流组成灵活设置?自行车道宽度大小对行人和自行车的运行又有何影响?因此, 本文基于上述行人和自行车的动力学模型, 利用Matlab进行了计算机仿真, 并对仿真结果进行了分析。在设有/未设自行车道的两种人行横道场景, 对行人和自行车混合交通流进行仿真。仿真场景如图5所示, 设置的人行横道长为50 m, 总宽度为8 m, 当存在自行车道时, 自行车道宽度在[0, 4] m区间变化, 仿真时间步为0.6 s。

3.1 仿真参数标定

建立的社会力模型包含许多参数, 参数的取值影响仿真的效果。所有参数可以分为两类:可测参数与不可测参数。一些参数如自行车和行人速度可以通过调查数据得到, 而作用力强度和影响范围参数无法直接得到, 因此本文采用Zeng等^[9]的标定方法, 并参考相关研究成果确定参数的合理值。标定过程如下:

(1)直接参考Zeng等^[9]和Li等^[10]的研究结果标定相关参数如视野范围、反应时间等。

(2)最大速度等参数通过调查数据直接标定。

(3)确定可测参数后, 利用最大似然估计法(参考Zeng等的方法)标定没有物理意义且无法测量的参数, 如作用力强度和范围。参数的标定需要获取自行车和行人的真实运动轨迹, 本文利用江晟等^{[11, 12]}的轨迹提取方法从视频数据中获取了自行车和行人的真实运动轨迹。

柳莺路和聚业大街交叉口在2015年经过改造成为长春市“ 绿道” , 以满足骑行者锻炼需求, 该交叉口在人行横道处设置了自行车道线。以此交叉口作为调查地点, 获取行人和自行车运行轨迹, 标定模型相关参数。参数的标定结果如表1所示, 在置信水平为95%时, p值表明参数估计值是有效的。

表1 参数标定结果 Table 1 Calibration results of parameters

参数	公式	估计值	p值
行人之间作用力强度 $\begin{matrix} A_{α}^{1} \end{matrix}$	4	1.15	0.00
自行车之间作用力强度 $\begin{matrix} A_{i}^{1} \end{matrix}$	4	2	0.04
行人之间作用力影响距离 $\begin{matrix} B_{α}^{1} \end{matrix}$ /m	4	2	0.01
自行车之间作用力影响距离 $\begin{matrix} B_{i}^{1} \end{matrix}$ /m	4	3	0.01
边界对行人作用力强度A_{α B}	10	5	0.03
边界对行人作用力影响距离B_{α B}/m	10	0.1	0.04
边界对自行车作用力强度A_iB/m	10	8	0.00
边界对自行车作用力影响距离B_iB/m	10	0.5	0.05
行人与自行车之间作用力强度A_{α i}	14	2.25	0.02
行人与自行车之间作用力影响距离B_{α i}/m	14	3	0.04
自行车之间跟随力强度 $\begin{matrix} A_{ij}^{f} \end{matrix}$	15	16	0.03
自行车之间跟随力影响距离 $\begin{matrix} B_{ij}^{f} \end{matrix}$ /m	15	4	0.01
自行车道线对行人斥力强度 $\begin{matrix} A_{bα}^{r} \end{matrix}$	18	0.02	0.00
自行车道线对行人斥力影响范围 $\begin{matrix} B_{bα}^{r} \end{matrix}$	18	0.3	0.00
自行车道线对行人引力强度 $\begin{matrix} A_{bα}^{a} \end{matrix}$	18	0.07	0.01
自行车道线对行人引力影响范围 $\begin{matrix} B_{bα}^{a} \end{matrix}$	18	0.7	0.02
自行车道线对自行车斥力强度 $\begin{matrix} A_{bi}^{r} \end{matrix}$	19	0.01	0.04
自行车道线对自行车斥力影响范围 $\begin{matrix} B_{bi}^{r} \end{matrix}$	19	0.3	0.01
自行车道线对自行车引力强度 $\begin{matrix} A_{bi}^{a} \end{matrix}$	19	0.04	0.01
自行车道线对自行车引力影响范围 $\begin{matrix} B_{bi}^{a} \end{matrix}$	19	0.9	0.00
常数ε ₁	15	2
常数ε ₂	15	0.5
各向异性λ _α	6.16	0.3
行人半径r_α/m		-0.3
自行车半径r_i/m		-0.6
行人适应时间τ _α/s	3	0.5
自行车适应时间τ _i/s	3	0.5
行人期望速度 $\begin{matrix} v_{α}^{0} \end{matrix}$ (t)/(m· s^-1)	3	1.34
自行车期望速度 $\begin{matrix} v_{i}^{0} \end{matrix}$ (t)/(m· s^-1)	3	2.21

表1 参数标定结果 Table 1 Calibration results of parameters

3.2 模型验证

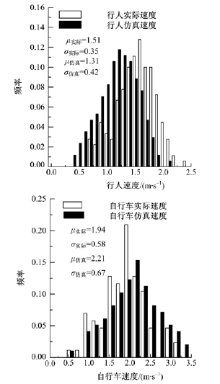
为排除偶然因素的影响, 并得到准确数据, 在同一仿真条件下, 进行了100次仿真实验, 记录所有行人和自行车的过街平均速度。然后分别对行人和自行车的时间和仿真速度进行对比, 如图8所示。根据实际速度和仿真速度(平均速度和方差)的对比发现, 修正的模型是有效的。

	Figure Option View Download New Window
	图8 实际速度与仿真速度对比Fig.8 Speed histograms of bikes and pedestrians observed data and simulation results

3.3 自行车道设置分析

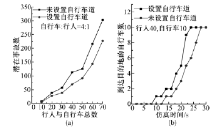
图9描述了自行车道的设置与否对自行车和行人的安全性以及自行车释放规律的影响。为减小自行车与行人比例对仿真的影响, 将自行车与行人的比例固定为4∶ 1, 自行车道宽度设为3 m; 图9(b)中行人数为40, 自行车为10。

	Figure Option View Download New Window
	图9 自行车道设置与否对行人和自行车的影响Fig.9 Impact of cyclist path on pedestrian and bike

由图9(a)可知, 无论是否设置自行车道, 随着行人和自行车总数的增加, 行人与自行车之间的潜在事故数都会增加; 而设置自行车道后, 行人和自行车被有效分离, 它们之间的冲突和相互作用降低, 混合交通流的潜在事故数随之减少, 这说明设置自行车道对于提高行人过街安全性是有效的。图9(b)表明, 经过相同的仿真时间, 设置自行车道的仿真环境中到达目的地的自行车数大于未设置自行车道中环境中到达目的地的自行车数; 并且相同条件下, 设置自行车道后, 所有自行车到达目的地的时间为23 s, 比未设置自行车道时所有自行车的过街时间少(28 s)。这是因为, 未设置自行车道的环境下, 行人占据混合交通流的主导地位, 自行车受行人干扰较大, 自行车的过街速度被迫降低到与行人接近的速度, 导致自行车过街时间增加。

3.4 自行车道宽度设置分析

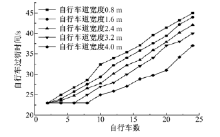
为研究自行车道宽度对自行车释放的影响, 本次仿真中, 自行车与行人总数为50。不同自行车道宽度条件下的自行车道过街时间如图10所示。

由图10可知:自行车道宽度保持不变的条件下, 自行车的过街时间随着自行车数目的增加而增加; 在自行车数目保持不变的条件下, 自行车的过街时间随着自行车道宽度的增加而减少, 这是因为当自行车数量固定时, 自行车道宽度越大, 自行车的行走自由性也愈大, 受行人的干扰也越小, 自行车能够保持较大的速度过街, 到达目的地所需时间就少, 这与实际交通流运行相符。此外, 当自行车道宽度达到3.2 m时, 在自行车数量小于6时, 过街时间保持不变; 自行车道为4 m时, 自行车数量小于8时, 自行车过街时间也保持不变, 因为这种仿真条件下, 自行车有足够的行驶空间, 且受到其他个体的干扰较小, 能以期望速度过街。

	Figure Option View Download New Window
	图10 自行车道宽度对自行车过街时间的影响Fig.10 Influence of cyclist̓s path width on crossing time

4 结束语

在基本社会力模型的基础上, 充分考虑自行车道的设置对行人以及自行车的影响, 引入自行车道对自行车和行人的作用力以及自行车之间的跟随力, 提出了用于仿真自行车和行人过街混合交通流的改进社会力模型。数值模拟分析发现, 设置自行车道能够有效分离行人和自行车, 并提高自行车和行人混合交通的运行效率; 此外, 在自行车流中模拟得到了部分自行车的跟随和自组织现象, 与实际交通观测相符; 随后, 分析了自行车道宽度对自行车过街时间的影响, 发现随自行车道宽度增加, 自行车过街时间随之减少。是否设置自行车道以及如何设置自行车道既能有效利用人行横道资源又能保证行人和自行车的安全, 是重点需要考虑的问题, 改进的社会力模型虽然能够重现自行车与行人混合交通流的运行情况, 但是本文却并没有得到详细的自行车道设置方法(设置临界流量和设置宽度), 也没有考虑超车时自行车之间的相互作用, 这将是作者下一步的研究方向。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Papadimitriou E, Yannis G, Golias J. A critical assessment of pedestrianbehavior models[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2009, 12(3): 242-255. [本文引用:1]
[2]	Helbing D, Molnar P. Social force model for pedestrian dynamics[J]. Physical Review E, 1995, 51(5): 4282. [本文引用:2]
[3]	Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic[J]. Nature, 2000, 407(6803): 487-490. [本文引用:2]
[4]	Helbing D, Farkas I J, Molnar P, et al. Simulation of pedestrian crowds in normal and evacuation situations[J]. Pedestrian and Evacuation Dynamics, 2002, 21(2): 21-58. [本文引用:2]
[5]	Helbing D, Buzna L, Johansson A, et al. Self-organized pedestrian crowd dynamics: Experiments, simulations, and design solutions[J]. Transportation Science, 2005, 39(1): 1-24. [本文引用:2]
[6]	Apel M. Simulation of pedestrian flows based on the social force model using theverlet link cell algorithm [D]. The Republic of Poland : Institute of Computing Science, Poznan University of Technology, 2004. [本文引用:1]
[7]	Johansson A. Pedestrian simulations with the social force model [D]. Dresden, Germany: Institute for Transport & Economics, Dresden University of Technology, 2004. [本文引用:1]
[8]	Moussaïd M, Helbing D, Garnier S, et al. Experimental study of the behavioural mechanisms underlying self-organization in human crowds[J]. Proceedings of the Royal Society of London B: Biological Sciences, 2009: 276(1668): 2755-2762. [本文引用:1]
[9]	Zeng W, Chen P, Nakamura H, et al. Application of social force model to pedestrian behavior analysis at signalized crosswalk[J]. Transportation Research Part C: Emerging Technologies, 2014, 40: 143-159. [本文引用:3]
[10]	Li M, Shi F, Chen D. Analyze bicycle-car mixed flow by social force model for collision risk evaluation[C]∥The 3rd International Conference on Road Safety and Simulation, Washington, DC, USA, 2011: 1-22. [本文引用:1]
[11]	江晟, 王殿海, 陈永恒, 等. 基于视频的行人运动轨迹再现与过街行为表达[J]. 东南大学学报: 自然科学版, 2012, 42(6): 1233-1237. Jiang Sheng, Wang Dian-hai, Chen Yong-heng, et al. Pedestrian movement trajectory reappearance and crossing feature expression based on video processing[J]. Journal of Southeast University (Natural Science Edition), 2012, 42(6): 1233-1237. [本文引用:1]
[12]	江晟. 混合交通视频检测关键技术研究 [D]. 长春: 吉林大学交通学院, 2013. Jiang Sheng. Research on key technologies of mixed traffic video detection [D]. Changchun: College of Transportation, Jilin University, 2013. [本文引用:1]

2009

0.0

... 对行人和自行车运动机制建模对道路行人设施的安全性评价和人行横道的通行能力评估都有至关重要的作用^[1] ...

1995

0.0

... 基于此,Helbing等^[2]在1995年构建了用于模拟行人在空间运动的社会力模型,该模型将行人与外界的相互作用量化为斥力和引力,最初社会力模型只建立了行人与行人以及行人与障碍物间的作用力 ...

... 在Helbing等^[2,3,4,5]的研究基础上,Apel^[6]、Johansson^[7]完善了行人自驱力方向权重方程,引入一个大于0且小于1的各向异性系数来反映行人对周围行人的影响强弱 ...

2000

0.0

... 2000年Helbing等^[3]考虑行人的随机波动特性对模型的参数进行了修正 ...

2002

0.0

... 2002年Helbing等^[4]在基本社会力模型的基础上,引入了行人的空间需求特性,考虑在拥挤条件下行人对其他行人的排斥力以及相互躲避的切向滑动力 ...

2005

0.0

... 2005年Helbing等^[5]认为行人期望速度的变化仅由自驱力决定,而实际中,周围行人的速度也影响着行人的期望速度,如果周围行人速度很快,行人期望速度也会改变 ...

2004

0.0

2004

0.0

2009

0.0

... Moussaid等^[8]通过对行人实际运动数据的分析发现,两个行人运动方向的夹角和他们之间的距离严重影响着行人速度的变化,通过数据拟合,建立了行人运动转角大小与行人运动方向夹角及行人间距的经验模型 ...

2014

0.0

... Zeng等^[9]构建了人行通道上的改进社会力模型,分析得出行人的转角和速度大小改变都服从正态分布,模型考虑了机动车以及信号灯对行人过街的影响,并建立了相关的社会力模型方程 ...

... 以往研究中,期望位置是随机的,本文行人期望位置分布采用Zeng等^[9]建立的行人期望位置的分布模型,即利用韦布尔分布构建了如下行人期望位置的分布模型: ...

... (1)直接参考Zeng等^[9]和Li等^[10]的研究结果标定相关参数如视野范围、反应时间等 ...

2011

0.0

... (1)直接参考Zeng等^[9]和Li等^[10]的研究结果标定相关参数如视野范围、反应时间等 ...

2012

0.0

. 2012, 42(6):1233-1237 DOI:doi:10.3969/j.issn.1001-0505.2012.06.038

Pedestrian movement trajectory reappearance and crossing feature expression based on video processing

基于视频的行人运动轨迹再现与过街行为表达

Jiang Sheng , Wang Dian-hai , Chen Yong-heng

江晟, 王殿海, 陈永恒

摘　要：针对行人运动轨迹再现及表达的问题,结合视频检测技术,提出一种结合时空上下文信息的行人运动特征提取和轨迹跟踪算法,并在视频标定计算中引入中心偏移量,改进了共线模型中不考虑镜头畸变的缺点,提高了标定精度.利用该算法对实际视频进行处理,获取多组行人运动参数和轨迹曲线,再将该算法提取的数据与共线标定方法的计算数据及人工调查得到的真实数据进行对比,验证所提算法的准确性.最后定量分析了几种行人过街行为,对过街行为相应的轨迹特征状态进行了表达,为行人交通组织和控制提供支持.

... 参数的标定需要获取自行车和行人的真实运动轨迹,本文利用江晟等^[11,12]的轨迹提取方法从视频数据中获取了自行车和行人的真实运动轨迹 ...

2013

0.0

. 2013, :-

Research on key technologies of mixed traffic video detection [D]. Changchun:College of Transportation,

混合交通视频检测关键技术研究 [D]

Jiang Sheng.

江晟

我国城市当前面临严峻的混合交通问题，需要通过智能化交通进行解决。而混合交通参数的高效、准确提取是智能化交通管理与控制的基础。目前常规的检测器难以满足混合交通参数提取的需求，迫切需要开发一种有针对性的混合交通检测系统。因此，混合交通视频检测技术的研究及相应系统的开发对于提高城市交通控制的实时性和准确性具有重要意义，对有效进行交通管理和保障交通安全具有重要作用。但是由于目前混合交通视频检测关键技术研究不足，使得混合交通视频检测系统的开发与实现受到严重限制。本文针对这一问题，结合混合交通视频检测的实际需求，对普适性的摄像机参数标定、混合交通前景信息提取和补偿、混合交通快速分类和识别、混合交通多运动目标跟踪和遮挡处理等关键技术进行了研究和讨论。论文完成的主要科研工作及取得的主要科研成果概括如下： (1)基于像素角映射的摄像机标定算法当前对于摄像机标定的问题研究较多，但以往的标定方法在适应性和快速性方面存在一定的问题。本文在前人研究的基础上，提出了基于像素角映射的摄像机标定算法。即在针孔成像线性模型的基础上，分别考虑了像素与像素角、像素角与世界坐标两组非线性映射关系，并根据混合交通视频检测的实际情况对标定算法进行了简化。同时引入摄像机高度和倾角等参数，扩大了标定算法的适用范围。最后通过试验对比验证了本文提出的标定算法具有检测精度高、适用范围广、灵活性强、鲁棒性好等优点，具有良好的工程实用价值。 (2)结合历史信息的混合交通前景提取和补偿算法针对混合交通场景的复杂性，本文在利用分段加权直方图(Partition WeightedHistogram, PWH)背景模型获取背景图像和背景边缘的基础上，通过引入历史信息来改进传统的边缘检测算法。首先通过将当前边缘信息、背景边缘信息及历史信息进行对比，经过推理和二次分析剔除背景边缘信息，获取前景边缘信息。然后通过融合差分信息，利用种子点生长法实现前景轮廓的补偿与修正，提取出能够满足混合交通分类识别需求的前景轮廓信息。最后，结合本文前景提取算法实现了阴影处理与夜间检测。 (3)结合极限学习机(ELM)训练的混合交通快速分类识别算法针对混合交通视频检测算法常常因为缺乏有效的分类特征而导致识别精度低以及传统智能算法学习计算量大而导致实时性差的问题，在以往研究的基础上，提出了结合极限学习机(Extreme Learning Machine, ELM)训练的混合交通快速分类识别算法。该算法以边缘轮廓偏心率向量为分类特征，并利用等角度间隔抽样的方法对边缘轮廓偏心率向量进行了维数统一，克服了以往算法识别精度低的问题。再通过将极大极小偏心距的比值引入到混合交通特征表达中，克服了行人和自行车特征区分度不高的问题。最后在特征选取和表达的基础上结合ELM的分类机制对混合交通进行了快速分类识别，克服了采用支持向量机(Support Vector Machine, SVM)等传统智能算法耗时长的问题，实现了混合交通的快速、准确识别。 (4)多目标跟踪和遮挡处理机制针对混合交通中多目标跟踪及遮挡处理难以实现的问题，提出了基于Kalman滤波和PCA-SIFT(Principal ComponentsAnalysis applied to SIFT)匹配的方法进行多目标跟踪和遮挡处理。利用Kalman滤波结合真实世界参数进行前景多目标预测，判断是否出现遮挡现象。通过对遮挡现象的判断结果选取不同的跟踪策略：若未发现遮挡，则采用基于世界坐标约束的Kalman滤波进行跟踪，保证跟踪的快速性；若发现遮挡，则结合预测信息锁定靶区域，缩小检索范围，再利用PCA-SIFT算法进行快速匹配，完成遮挡还原，实现了多运动目标的预测及跟踪，确保了跟踪结果的准确性及快速性。最后，在实际交通场景中对本文开发的检测系统进行了测试，结果表明：该系统能够良好地完成混合交通视频检测任务，准确提取多种混合交通参数。最后对本文的研究内容进行总结和展望。总结了本文所取得的研究成果以及创新点，针对本文研究的不足提出了下一步的研究计划。

... 参数的标定需要获取自行车和行人的真实运动轨迹,本文利用江晟等^[11,12]的轨迹提取方法从视频数据中获取了自行车和行人的真实运动轨迹 ...