基于活塞形状的空气弹簧动特性分析与参数优化

引用本文

李静, 丁明慧, 李立刚, 陈立军. 基于活塞形状的空气弹簧动特性分析与参数优化. 2018, 48(2): 355-363
LI Jing, DING Ming-hui, LI Li-gang, CHEN Li-jun. Dynamic characteristics analysis and optimization of air spring based on the piston shape. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 355-363 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170282
Permissions

基于活塞形状的空气弹簧动特性分析与参数优化

李静¹, 丁明慧¹, 李立刚², 陈立军³

1. 吉林大学汽车工程学院,长春 130022

2. 浙江亚太机电股份有限公司,杭州 311203

3.吉林大学大数据和网络管理中心,长春 130022

通信作者:陈立军(1960-),男,副研究员.研究方向:计算机应用.E-mail:clj@jlu.edu.cn

作者简介:李静(1974-),男,教授,博士生导师. 研究方向:汽车底盘系统整车性能匹配及电控系统.E-mail:liye1129@163.com

基金项目:国家自然科学基金项目(51275206)

摘要

考虑活塞圆弧过渡,采用曲面积分按活塞设计形状分阶段推导空气弹簧动特性精确模型,分析了活塞主要设计参数对空气弹簧动特性的影响规律,并进行了试验设计(DOE)灵敏度分析和参数优化。结果表明,该建模方法能较准确地预测空气弹簧动特性,为汽车用空气弹簧刚度设计匹配提供了一种较为经济实用的预估方法;基于空气弹簧活塞结构参数优化可以使空气弹簧在正常工作压力、推荐工作高度范围内工作的同时兼顾车辆自身的舒适性和空气弹簧的综合使用性能,具有一定的经济价值。

关键词: 车辆工程; 膜式空气弹簧; 动态特性; 活塞设计; 参数优化

中图分类号:TH212 文献标志码:A 文章编号:1671-5497(2018)02-0355-09

Dynamic characteristics analysis and optimization of air spring based on the piston shape

LI Jing¹, DING Ming-hui¹, LI Li-gang², CHEN Li-jun³

1.College of Automotive Engineering, Jilin University, Changchun 130022, China

2.Zhejiang Asia-pacific of Electronic Company Limited, Hangzhou 311203, China

3.Big Data and Network Management Center, Jilin University, Changchun 130022,China

Abstract

The precise design of the dynamic stiffness of air spring is one of the key issues to accurately match the dynamic stiffness of the vehicle in the predevelopment stage. Considering the transition of the piston circular area, a method is proposed to get the accurate dynamic characteristics model of the air spring, which is based on the design of the piston shape in different stages according to the surface integral. The influence of the main design parameters on the dynamic characteristics of the air spring is studied. The experimental design sensitivity analysis and parameter optimization are carried out. Results show that the model can accurately predict the dynamic characteristics of the air spring and provide an economical and practical prediction method of the stiffness design of the air spring used in automobiles. When the air spring is in normal working pressure and recommended working height range, the optimization of structural parameters of the air spring piston can simultaneously take into account the comfort of vehicle itself and the comprehensive performance of the air spring and has certain economic value.

Key words: vehicle engineering; diaphragm air spring; dynamic characteristics; piston design; parameter optimization

Show Figures

0 引言

现有的空气弹簧模型主要有简单模型、Nishimura、VAMPIRE、SIMPACK、GENSYS等5种模型^[1], 适用于汽车产品预开发阶段的仿真匹配, 需要试验数据做大量的参数辨识, 国内外学者基于以上几种模型对空气弹簧的动力学行为及影响因素进行了大量研究^{[2, 3, 4]}, 取得了丰硕的研究成果。大多数学者在对空气弹簧的特性研究中关于有限元分析^{[5, 6, 7]}的方法较多, 能较为准确地分析空气弹簧气囊的受力, 但此类方法需要建立复杂的有限元模型, 且分析过程耗时较长; 也有采用拟合试验数据^{[8, 9, 10]}的方法, 在整车动力学仿真匹配时可以通过插值计算得到空气弹簧悬架刚度, 此类方法适合验证空气弹簧建模分析方法的准确性, 但不能预测空气弹簧动特性; 现有的基于结构的理论分析^{[11, 12, 13]}方法中, 大多数学者或多或少地忽略了空气弹簧的活塞结构, 而实际上空气弹簧活塞形状对空气弹簧动刚度影响很大, 其由锥面、柱面和弧面中的一种或多种组合而成, 因此有必要基于活塞实际形状对空气弹簧进行特性分析。

在目前公开发表的论文中, 大多数学者主要以汽车平顺性为目标对空气悬架的刚度、阻尼进行优化匹配^{[14, 15, 16, 17]}, 通过电控系统控制空气弹簧的内压, 从而调节空气弹簧的刚度, 很少有人进一步地对空气弹簧结构设计参数进行优化。仅仅从控制的角度出发通过调节空气弹簧的内压达到改变空气弹簧的刚度不能很好地考虑空气弹簧的损伤及寿命问题, 在对空气弹簧进行设计匹配时, 应该考虑空气弹簧的安装高度、在汽车上的布置位置、工作压力范围、轴行程等方面的问题, 因此, 需要对空气弹簧的结构设计参数进行合理的优化, 以使空气弹簧在正常工作压力、推荐工作高度范围内工作时减少损伤, 延长使用寿命。

本文考虑活塞圆弧过渡, 将空气弹簧活塞简化为锥面、柱面和弧面的接合, 采用曲面积分方法推导了3种曲面上空气弹簧动特性的精确计算公式, 并通过试验验证了该模型的准确性。基于该模型对活塞结构参数进行了试验设计(DOE)灵敏度分析, 考虑空气弹簧动刚度设计和匹配, 建立了多目标优化模型, 采用统一目标函数法对空气弹簧活塞设计参数进行优化。在装有空气弹簧悬架的汽车产品预开发阶段准确地匹配空气弹簧的动刚度, 将大大缩短产品开发后期的试验匹配和调试的周期。

1 空气弹簧动态特性理论分析

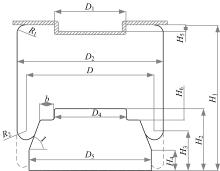
基于前进牌橡胶空气弹簧662 N^[18], 考虑活塞弧面的膜式空气弹簧的计算模型如图1所示。图中:D₁为气囊上止口直径; D₂为气囊内径; D为卷耳中心直径; D₄为气囊下止口直径; D₅为活塞柱面直径; H₁为气囊有效高度; H₂为活塞高度; H₃为卷耳中心高度; H₄为活塞底座圆台高度; H₅为气囊上止口高度; H₆为气囊下止口高度; R₁为气囊圆角; R₂为卷耳半径; ∠1为活塞锥面倾斜角。假设空气弹簧气囊外径和气囊内径线长度保持不变。

	Figure Option View Download New Window
	图1 空气弹簧的计算模型Fig.1 Air spring model

为便于计算, 引入活塞肩台宽度b(随着∠1而变化)和中间变量h两个变量:

b= $\begin{matrix} \frac{(D_{5} - D_{4})}{2} \end{matrix}$ - $\begin{matrix} \frac{H_{2} - H_{6} - H_{4}}{tan∠ 1} \end{matrix}$ (1)

h= $\begin{matrix} (\frac{D_{2}}{2} - \frac{D_{4}}{2} - b) \end{matrix}$ tan∠1(2)

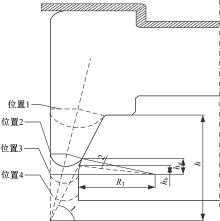
如图2所示, ∠2为空气弹簧活塞圆弧曲面对应的圆心角一半; h_a为活塞圆弧曲面总高; h_b为活塞圆弧曲面中心高; R₃为活塞弧面半径。

∠2= $\begin{matrix} \frac{90 ° - ∠ 1}{2} \end{matrix}$ (3)

h_b=R₃sin∠2(4)

h_a=R₃sin2∠2(5)

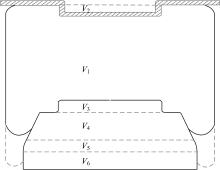
分阶段推导变截面膜式空气弹簧的相关特性公式, 图3为活塞曲面各阶段的端点位置。图中:V₁为空气弹簧对外表现的总体积; V₂为上止口体积; V₃为下止口体积; V₄为活塞锥面圆台体积; V₅为活塞弧面圆台体积; V₆为活塞柱面圆台体积。

	Figure Option View Download New Window
	图2 活塞曲面分段示意图Fig.2 Sketch of piston surface segmentation

	Figure Option View Download New Window
	图3 空气弹簧体积模型Fig.3 Volume model of air spring

位置1:卷耳与活塞锥面相切的最高点h₁。

h₁= $\begin{matrix} \frac{h}{sin∠ 1} \end{matrix}$ -(h-H₂+H₆)(6)

位置2:卷耳与活塞锥面相切的最低点h₂。

h₂= $\begin{matrix} \frac{H_{4} + h_{a} - h_{b} + h - H_{2} + H_{6}}{sin∠ 1} \end{matrix}$ -(h-H₂+H₆) (7)

位置3:卷耳与活塞弧面相切的最低点h₃。

h₃=H₄-h_b (8)

位置4:卷耳与活塞圆柱面相切的最低点h₄。

h₄= $\begin{matrix} \frac{D_{2} - D_{5}}{4} \end{matrix}$ (9)

通过以上4个位置可将活塞曲面划分为:h₄< H₃< h₃、h₃< H₃< h₂和h₂< H₃< h₁三个部分。

1.1 活塞作用高度

活塞作用高度H₃与空气弹簧高度H₁的关系为:

H₁= $\begin{matrix} \{\begin{matrix} L_{0} - \frac{π R_{1}}{2} - π R_{2} - (H_{4} - h_{b} - H_{3}) - \\ \frac{π R_{3} ∠ 2}{90 °} - \frac{H_{2} - H_{6} - H_{4} - h_{a} + h_{b}}{sin∠ 1} - \\ b + R_{1} + H_{3}, h_{4} < H_{3} < h_{3} \\ L_{0} - \frac{π R_{1}}{2} - \frac{π R_{2} (∠ B + 90 °)}{180 °} - \\ \frac{π R_{3} (2 ∠ 2 + ∠B - 90 °)}{180 °} - \\ \frac{H_{2} - H_{6} - H_{4} - h_{a} + h_{b}}{sin∠ 1} + \\ H_{3} - b + R_{1}, h_{3} < H_{3} < h_{2} \\ L_{0} - \frac{π R_{1}}{2} - \frac{π R_{2} (∠ 1 + 90 °)}{180 °} - \\ b + R_{1} + H_{3} - \\ [\frac{h}{sin∠ 1} - (H_{3} + h - H_{2} + H_{6})], \\ h_{2} < H_{3} < h_{1} \end{matrix} \end{matrix}$ (10)

式中:L₀ 为气囊初始经线长度; 中间变量∠B=cos^-¹ $\begin{matrix} (\frac{H_{3} - H_{4} + h_{b}}{R_{3} + R_{2}}) \end{matrix}$ 。

1.2 有效面积及其变化率

卷耳半径在活塞曲面的变形为:

R₂= $\begin{matrix} \{\begin{matrix} \frac{D_{2} - D_{5}}{4}, h_{4} < H_{3} < h_{3} \\ \frac{{(H_{3} - H_{4} + h_{b})}^{2}}{4 R_{3} + D_{2} - D_{5}} + \frac{D_{2} - D_{5}}{4}, \\ h_{3} < H_{3} < h_{2} \\ (H_{3} + h - H_{2} + H_{6}) \cdot \tan \frac{90 ° - ∠ 1}{2}, \\ h_{2} < H_{3} < h_{1} \end{matrix} \end{matrix}$ (11)

空气弹簧的有效工作面积为:

A=π $\begin{matrix} {(\frac{D_{2} - 2 R_{2}}{2})}^{2} \end{matrix}$ (12)

空气弹簧的有效面积变化率与位移的关系为:

$\begin{matrix} \frac{dA}{d H_{3}} \end{matrix}$ =2π · · · $\begin{matrix} \frac{dD}{d H_{3}} \end{matrix}$ =-π D· $\begin{matrix} \frac{d R_{2}}{d H_{3}} \end{matrix}$ (13)

将式(11)代入式(12)(13)即可得到空气弹簧有效面积、有效面积变化率与高度H₃的关系式。

1.3 有效体积

如图3所示, 空气弹簧的工作体积为:

V=V₁-V₂-V₃-V₄-V₅-V₆+V_f(14)

式中:V_f为附加气室体积。

V₁=π $\begin{matrix} {(\frac{D_{2}}{2})}^{2} \end{matrix}$ · $\begin{matrix} (H_{1} - R_{1} - H_{3}) \end{matrix}$ + $\begin{matrix} \frac{π R_{1}^{2}}{4} \end{matrix}$ · 2π $\begin{matrix} (\frac{D_{2}}{2} - R_{1}) \end{matrix}$ +π $\begin{matrix} {(\frac{D_{2}}{2} - R_{1})}^{2} \end{matrix}$ · R₁+ $\begin{matrix} \frac{π R_{2}^{2}}{2} \end{matrix}$ · 2π $\begin{matrix} (\frac{D_{2}}{2} - R_{2}) \end{matrix}$ (15)

V₂=π $\begin{matrix} {(\frac{D_{1}}{2})}^{2} \end{matrix}$ · H₅(16)

V₃=π $\begin{matrix} {(\frac{D_{4}}{2})}^{2} \end{matrix}$ · H₆(17)

V₄= $\begin{matrix} \frac{π h_{m}}{3} \end{matrix}$ · $\begin{matrix} (R_{m}^{2} + R_{m} \cdot r_{m} + r_{m}^{2}) \end{matrix}$ (18)

式中:圆台的高h_m=H₂-H₆-H₄-h_a+h_b; 圆台底面半径R_m= $\begin{matrix} \frac{h_{m}}{tan∠ 1} \end{matrix}$ +b+ $\begin{matrix} \frac{D_{4}}{2} \end{matrix}$ ; 圆台顶面半r_m=b+ $\begin{matrix} \frac{D_{4}}{2} \end{matrix}$ 。

V₅通过其底面圆面积积分得到, 其中V₅底面圆半径为:

$\begin{matrix} r_{V_{5}} \end{matrix}$ = $\begin{matrix} \frac{D_{2}}{2} \end{matrix}$ - $\begin{matrix} (\frac{{(t - H_{4} + h_{b})}^{2}}{4 R_{3} + D_{2} - D_{5}} + \frac{D_{2} - D_{5}}{4}) \end{matrix}$ · (1+sin∠B) (19)

V₅= $\begin{matrix} \int_{h_{3}}^{h_{2}} \end{matrix}$ π $\begin{matrix} r_{V_{5}}^{2} \end{matrix}$ dt(20)

将式(19)代入式(20)得到体积V₅。

V₆=π $\begin{matrix} {(\frac{D_{5}}{2})}^{2} \end{matrix}$ · $\begin{matrix} (H_{4} - h_{b} - H_{3}) \end{matrix}$ (21)

将式(15)~(21)代入式(14)中, 即得其空气弹簧的有效体积。上述分析中, 认为空气弹簧卷耳变形发生在活塞柱面上, 即h₄< H₃< h₃。当空气弹簧的卷耳变形发生在圆弧面上时, 即h₂< H₃< h₁阶段时:

V₅=0(22)

V₆=0(23)

当空气弹簧的卷耳变形发生在圆弧面上时, 即h₃< H₃< h₂阶段时:

V₅= $\begin{matrix} \int_{H_{3}}^{h_{2}} \end{matrix}$ π $\begin{matrix} r_{V_{5}}^{2} \end{matrix}$ dt(24)

V₆=0 (25)

1.4 刚度

空气弹簧的体积变化率为:

= $\begin{matrix} \frac{d H_{1}}{dx} \end{matrix}$ · $\begin{matrix} \frac{dV}{d H_{1}} \end{matrix}$ = $\begin{matrix} \frac{d H_{1}}{dx} \end{matrix}$ · $\begin{matrix} \frac{d H_{3}}{d H_{1}} \end{matrix}$ · $\begin{matrix} \frac{dV}{d H_{3}} \end{matrix}$ (26)

将式(14)代入式(26)得:

$\begin{matrix} \frac{dV}{d H_{3}} \end{matrix}$ = $\begin{matrix} \{\begin{matrix} π {(\frac{D_{2}}{2})}^{2} (\frac{d H_{1}}{d H_{3}} - 1) - π {(\frac{D_{5}}{2})}^{2}, \\ h_{4} < H_{3} < h_{3} \\ \frac{2 (H_{3} - H_{4} + h_{b})}{4 R_{3} + D_{2} - D_{5}} \cdot \\ [2 π^{2} R_{2} (\frac{D_{2}}{2} - R_{2}) - π^{2} R_{2}] + \\ π {(\frac{D_{2}}{2})}^{2} (\frac{d H_{1}}{d H_{3}} - 1) - \\ π (\frac{D_{2}}{2} - R_{2} (1 + sin∠B)), \\ h_{3} < H_{3} < h_{2} \\ π {(\frac{D_{2}}{2})}^{2} (\frac{d H_{1}}{d H_{3}} - 1) + \\ \frac{π h_{m} cos∠ 1}{3} (2 R_{m} + r_{m}) + \\ [2 π^{2} R_{2} (\frac{D_{2}}{2} - R_{2}) - π^{2} R_{2}^{2}] \cdot \\ \tan \frac{90 ° - ∠ 1}{2} + \frac{π}{3} sin∠ 1 \cdot \\ (R_{m}^{2} + R_{m} \cdot r_{m} + r_{m}^{2}), \\ h_{2} < H_{3} < h_{1} \end{matrix} \end{matrix}$ (27)

空气弹簧的刚度为:

K=P_r-nA $\begin{matrix} (P_{r 0} + P_{a}) \end{matrix} \begin{matrix} {(\frac{V_{0}}{V})}^{n} \end{matrix}$ · · (28)

式中:P_r0为空气弹簧内部初始相对气压; P_r0+P_a为空气弹簧内部初始绝对气压; 为有效面积变化率; 为有效体积变化率; n为多变指数, 等温过程取1, 绝热过程取1.4, 本文计算空气弹簧的动态特性取值为1.33^[11]。

1.5 负荷

空气弹簧内部实时气压P_m为:

P_m=(P_r0+P_a) $\begin{matrix} {(\frac{V_{0}}{V})}^{n} \end{matrix}$ -P_a (29)

式中:P_m为空气弹簧内部初始相对气压; ( $\begin{matrix} {P_{r 0}}_{} \end{matrix}$ +P_a)为空气弹簧内部初始绝对气压。

空气弹簧的实时负荷为:

M= $\begin{matrix} \frac{P_{m} \cdot A}{g} \end{matrix}$ (30)

2 空气弹簧实例计算与试验验证

以贵州前进牌橡胶空气弹簧662 N^[23]为例对第1节所推导的空气弹簧特性计算公式进行仿真对比, 662 N空气弹簧参数如表1所示。

表1 662N空气弹簧参数 Table 1 Parameters of 662N air spring

2.1 静态负荷

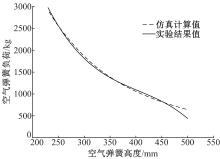
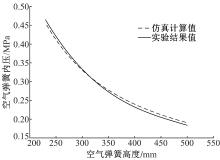
将662N空气弹簧总成调整到建议设计高度, 然后向橡胶空气弹簧总成内充入0.3 MPa空气, 关闭进气阀门, 保证空气弹簧总成在上下运动过程中不泄露, 测量出位移与负荷能力变化的曲线, 即变压曲线。将试验数据用最小二乘法进行三次多项式拟合, 静态负荷试验曲线与仿真曲线对比结果如图4所示。从图中可以看出, 0.3 MPa内压下的空气弹簧静态负荷仿真值与实验值一致性较好, 验证了基于结构的空气弹簧模型计算的准确性。

	Figure Option View Download New Window
	图4 0.3 MPa空气弹簧静态负荷Fig.4 Static load of air spring at 0.3 MPa

2.2 位移与气压曲线

位移-气压试验曲线与仿真曲线对比结果如图5所示, 由图可知, 0.3 MPa内压下的空气弹簧位移与气压的仿真值和实验值一致性较好, 验证了基于结构的空气弹簧模型计算的准确性。

	Figure Option View Download New Window
	图5 0.3 MPa空气弹簧位移与气压曲线Fig.5 Displacement and pressure curve of air spring at 0.3 MPa

3 空气弹簧动态特性分析

基于以上理论分析与模型的试验验证, 本节以活塞锥角为例, 将活塞锥角设置为80° 和85° , 分析其对空气弹簧有效面积、有效体积、动刚度的影响, 其余因素的影响可通过灵敏度分析来实现。

3.1 有效面积

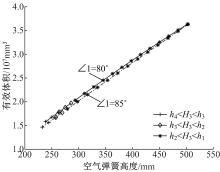
空气弹簧有效面积如图6所示, 活塞锥角对有效面积最小值影响较大, 当∠1=80° 时, 其最小值为6.92× 10⁴ mm², 当∠1=85° 时, 其最小值为7.48× 10⁴ mm²。活塞锥角增大6.25%, 空气弹簧有效面积最小值增大8.7%。

	Figure Option View Download New Window
	图6 活塞锥角对有效面积的影响Fig.6 Effect of piston cone angle on effective area

3.2 有效体积

空气弹簧有效体积如图7所示, 当∠1=80° 时, 空气弹簧有效体积最小值为1.53× 10⁷ mm³。当∠1=85° 时, 空气弹簧有效体积最小值为1.38× 10⁷ mm³。活塞锥角增大6.25%, 空气弹簧有效体积最小值减小9.8%。活塞锥角改变对空气弹簧有效体积的最大值影响较小。

	Figure Option View Download New Window
	图7 空气弹簧体积随高度变化曲线Fig.7 Variation of air spring volume with height

3.3 动刚度

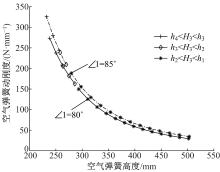
空气弹簧动刚度如图8所示, 当∠1=80° 时, 空气弹簧动刚度为29.38~294.38 N/mm。当∠1=85° 时, 空气弹簧动刚度为34.46~372.4 N/mm。活塞锥角增大6.25%, 空气弹簧动刚度最小值增大17.29%, 最大值增大26.5%, 即活塞锥角平均每增加1%, 空气弹簧动刚度最小值增大2.77%, 最大值增大4.24%。

	Figure Option View Download New Window
	图8 空气弹簧动刚度随高度变化曲线Fig.8 Variation of air spring stiffness with height

4 空气弹簧参数优化

基于第1节公式的推导, 第3节以活塞锥角为例分析其对空气弹簧性能的影响, 但限于篇幅限制及时间成本等因素, 实际工程中不可能将空气弹簧的每一个设计参数都如第3节分析。为了快速准确地分析空气弹簧各个设计参数对其动刚度的影响, 故引入灵敏度分析。同时, 为了进一步获得空气弹簧的最优设计刚度, 需对空气弹簧活塞设计参数进行优化。

4.1 变量灵敏度分析

本文对活塞形状参数进行灵敏度分析, 选取空气弹簧安装高度(320± 10)mm行程范围内的线性刚度为目标, 以空气弹簧活塞形状的设计参数作为设计变量, 各参数取值范围如表2所示。

表2 设计变量及其变动范围 Table 2 Variation range of design variables

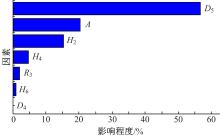
采用正交试验方法对其进行灵敏度分析计算, 分析结果如图9所示。由图可知, 活塞柱面直径对空气弹簧刚度影响最大, 对目标值的影响程度的大小依次为:活塞柱面直径> 活塞锥面倾角> 活塞高度> 活塞底座圆台高度> 活塞弧面半径> 气囊下止口高度> 活塞下止口直径。

	Figure Option View Download New Window
	图9 变量灵敏度分析Fig.9 Sensitivity analysis for variables

4.2 活塞形状参数优化

理想的空气弹簧的载荷-位移曲线形状呈反“ S” 形, 通过适当选择空气弹簧的结构设计参数, 可以使空气弹簧在正常工作压力、推荐工作高度范围内工作时刚度较小且变化小, 而在拉伸或压缩的边缘区段刚度逐渐增加, 其优点有包括:①空气弹簧在正常工作范围内拉压变形柔和, 振动频率较低, 提高汽车行驶平顺性; ②当因振动加剧产生较大的压缩或拉伸时, 空气弹簧刚度迅速增加, 从而减小振幅; ③能够保持在推荐的安装高度附近工作。

本文基于文献[17, 18], 在以提高汽车平顺性为目标, 对空气弹簧安装高度处的刚度优化匹配结果已知为前提, 基于前文推导的空气弹簧刚度模型, 进一步对活塞形状设计参数进行优化, 力求使空气弹簧在正常工作压力、安装高度(320± 10)mm在行程范围内工作时刚度保持为汽车平顺性最优刚度值, 设该优化目标为f₁(x)。选取满足空气悬架动挠度的空气弹簧拉伸极限位置和压缩极限位置的刚度达到最大为另外两个优化目标函数f₂(x)、f₃(x), 多目标优化模型为:

$\begin{matrix} \min_{x \in D} \end{matrix}$ f(x)= $\begin{matrix} \min_{x \in D} \end{matrix}$ f $\begin{matrix} [f_{1} (x), f_{2} (x), f_{3} (x)] \end{matrix}$ (31)

式中:D为可行域; $\begin{matrix} \min_{x \in D} \end{matrix}$ f₂(x)=- $\begin{matrix} \max_{x \in D} \end{matrix}$ f_{H_up}(x), f_{H_up}(x)为空气弹簧拉伸极限位置的刚度值; $\begin{matrix} \min_{x \in D} \end{matrix}$ f₃(x)= $\begin{matrix} \underset{x \in D}{- \max} \end{matrix}$ f_{H_low}(x), f_{H_low}(x)为空气弹簧压缩极限位置的刚度值。

文献[19]通过线性加权将多目标优化转化为单目标优化问题, 通过设定各个目标函数的不同权重, 得到一组解来逼近Pareto最优解集。此线性加权的归一化方法在处理3个及以上的多个优化目标时, 权重系数受优化者主观影响很大, 权重系数在目标空间中的等值面关系不直观, 且较难获得理想的最优解集。本文采用非归一化(Non-scalar)方法直接处理多个目标的优化问题, 克服了归一化方法必须将多个目标转化为单一目标的缺点, 优化过程中, 使所有解集的前沿最大限度地与Pareto前沿均匀接近。

如图9所示, 虽然通过灵敏度分析活塞柱面直径D₅对空气弹簧的动刚度影响最大, 但考虑到所匹配的空气悬架在汽车上的安装空间限制和底座安装尺寸确定的前提下, 参数优化时不考虑活塞横向设计尺寸。本文以活塞锥面倾角A、活塞高度H₂、活塞弧面半径R₃、活塞底座高度H₄为设计变量:

x=[A H₂R₃H₄]^T(32)

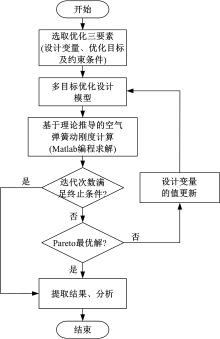
变量因子约束范围参考灵敏度分析中的变动范围, 由于梯度优化算法(Gradient optimization)能很好地解决非线性、连续问题, 故本文采用此优化方法对空气弹簧刚度进行最优设计分析, 图10为基于空气弹簧动刚度计算的活塞形状设计参数优化基本步骤。

	Figure Option View Download New Window
	图10 多目标优化设计流程图Fig.10 Flow diagram of multi-objective optimization

优化前、后空气弹簧的刚度特性曲线对比如图11所示, 优化结果如表3所示。

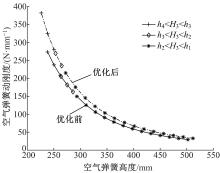	Figure Option View Download New Window
	图11 优化前、后的空气弹簧动刚度对比Fig.11 Comparison of dynamic stiffness of air spring before and after optimization

表3 空气弹簧刚度优化结果 Table 3 Optimization results of air spring stiffness

从优化结果可以看出, 在空气弹簧安装高度附近优化前、后基本保持一致, 满足刚度匹配要求; 在超过空气弹簧安装高度的拉伸过程中刚度优化前、后变化较小, 相比优化前最大拉伸位置处的刚度值, 优化后增大了1.2%; 在超过空气弹簧安装高度的压缩过程中刚度优化前、后变化较大, 相比优化前最大压缩位置处的刚度值, 优化后增大了38.7%。当因振动加剧空气弹簧产生较大的变形时, 空气弹簧刚度将迅速增大, 优化后的空气弹簧振幅更小, 有利于减小空气弹簧损伤, 延长使用寿命。通过修改空气弹簧结构设计参数可以快速分析和匹配空气弹簧刚度, 指导空气弹簧的设计。

5 结论

(1) 考虑空气弹簧活塞设计形状, 将活塞曲面划分为锥面、柱面和弧面并分区域推导的空气弹簧动特性模型具有较高的精度, 能够便捷地用于空气弹簧动刚度设计和匹配。

(2) 基于活塞设计形状的空气弹簧动特性模型具有较高的实用价值, 模型中所需的结构参数可方便地获取, 且根据结构设计参数能快速预测空气弹簧动刚度是否符合设计要求。

(3)考虑汽车用空气弹簧动刚度匹配对空气弹簧改进设计时, 应在要求的空气弹簧安装空间范围内, 将空气弹簧的活塞锥面倾角、活塞高度、活塞弧面半径和活塞底座高度作为主要参考因素。

(4)从活塞结构优化的角度考虑空气弹簧动刚度设计和匹配, 可以使空气弹簧在正常工作压力、推荐工作高度范围内工作, 减少损伤, 延长使用寿命, 具有一定的经济价值。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Presthus M. Derivation of air spring model parameters for train simulation [D]. Lulea: Lulea University of Technology, 2002. [本文引用:1]
[2]	Shimozawa K, Tohtake T. An air spring model with non-linear damping for vertical motion[J]. Quarterly Report of Rtri, 2008, 49(4): 209-214. [本文引用:1]
[3]	Hao L, Jaecheon L. Model development of automotive air spring based on experimental research[C]∥2011 Third International Conference on Measuring Technology and Mechatronics Automation, IEEE, 2011: 585-590. [本文引用:1]
[4]	Abid H J, Chen J, Nassar A. Equivalent air spring suspension model for quarter-passive model of passenger vehicles[J]. International Scholarly Research Notices, 2015: 974020. [本文引用:1]
[5]	Sun J. Calculation of vertical stiffness of air spring with FEM[C]∥ANSA & μETA Internation Conference, Thessaloniki, Greece, 2011. [本文引用:1]
[6]	Lin L, Wang T Y, Huang Y X, et al. Research and analysis of stiffness properties of new vehicle air spring[J]. Key Engineering Materials, 2014, 589: 729-734. [本文引用:1]
[7]	屠德新, 黄昌文, 陈毛权, 等. 基于 ABAQUS 的帘线参数对汽车空气弹簧垂向刚度影响的研究[J]. 汽车技术, 2011(2): 10-13. Tu De-xin, Huang Chang-wen, Chen Mao-quan, et al. Study on the influence of cord parameters on the vertical stiffness of air springs for vehicles based on ABAQUS[J]. Automobile Technology, 2011 (2): 10-13. [本文引用:1]
[8]	Asami T, Yokota Y, Ise T, et al. An approximate formula to calculate the restoring and damping forces of an air spring with a small pipe[J]. Journal of Vibration and Acoustics, 2013, 135(5): 1-9. [本文引用:1]
[9]	陈燎, 周孔亢, 李仲兴. 空气弹簧动态特性拟合及空气悬架变刚度计算分析[J]. 机械工程学报, 2010, 46(4): 93-98. Chen Liao, Zhou Kong-kang, Li Zhong-xing. Dynamic characteristics fitting of springs and numerical analysis of air suspensions with variant stiffness[J]. Journal of Mechanical Engineering, 2010, 46(4): 93-98. [本文引用:1]
[10]	陈双, 宗长富, 孙艳, 等. 可调刚度膜式空气弹簧特性试验研究[J]. 辽宁工业大学学报: 自然科学版, 2014, 34(3): 166-170. Chen Shuang, Zong Chang-fu, Sun Yan, et al. Test study of character of adjustable stiffness of diaphragm air springs[J]. Journal of Liaoning University of Technology (Natural Science Edition), 2014, 34(3): 166-170. [本文引用:1]
[11]	李滨, 陈无畏. 汽车膜式空气弹簧的分析与计算[J]. 合肥工业大学学报: 自然科学版, 2004, 27(10): 1191-1195. Li Bin, Chen Wu-wei. Analysis and calculation of diaphragm air spring of an automobile[J]. Journal of Hefei University of Technology(Natural Science), 2004, 27(10): 1191-1195. [本文引用:2]
[12]	唐传茵, 张义民, 李允公, 等. 单气室变截面空气弹簧刚度特性及影响因素分析[J]. 机械工程学报, 2014, 50(24): 137-144. Tang Chuan-yin, Zhang Yi-min, Li Yun-gong, et al. Analysis of stiffness characteristics and influencing factors based on single chamber cross-section air spring[J]. Journal of Mechanical Engineering, 2014, 50(24): 137-144. [本文引用:1]
[13]	胡德安, 甘亮亮, 丁飞, 等. 基于活塞形状改变的空气弹簧特性仿真研究[J]. 计算机仿真, 2012, 29(1): 331-334. Hu De-an, Gan Liang-liang, Ding Fei, et al. Simulation of stiffness character of diaphragm air spring based on change piston contour[J]. Computer Simulation, 2012, 29(1): 331-334. [本文引用:1]
[14]	陈静, 曹晓琳, 王登峰, 等. 重型商用车驾驶室空气悬置系统的匹配优化[J]. 吉林大学学报: 工学版, 2009, 39(5): 1125-1129. Chen Jing, Cao Xiao-lin, Wang Deng-feng, et al. Matching and optimization of heavy commercial vehicle cab air suspension system[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(5): 1125-1129. [本文引用:1]
[15]	姜圣, 卿启湘, 龙铝波. 基于多体力学的汽车空气弹簧悬架优化[J]. 工程设计学报, 2009, (03): 182-186. Jiang Sheng, Qing Qi-xiang, Long Lyu-bo. Optimization of air suspension parameters based on multi-body dynamic[J]. Journal of Engineering Design, 2009, 16(3): 182-186. [本文引用:1]
[16]	Sayyaadi H, Shokouhi N. New dynamics model for rail vehicles and optimizing air suspension parameters using GA[J]. Scientia Iranica, 2009, 16(6): 496-512. [本文引用:1]
[17]	徐强, 骆汉丰, 李亮. 重型牵引车空气悬架参数匹配优化[J]. 合肥学院学报: 自然科学版, 2014(3): 53-57. Xu Qiang, Luo Han-feng, Li Liang. Heavy tractor matching air suspension parameters optimization[J]. Journal of Hefei University(Natural Science), 2014(3): 53-57. [本文引用:1]
[18]	前进牌橡胶空气弹簧使用手册[Z/OL]. [2016-07-02]. http://wenku.baidu.com/link?url=xEqF33J_ExPhRADzsOwYXU07TcBe6jIE69ixLW3qcIoXA2iVjKDViF52NZRjI_5gkPY8h30TTuEgnArMS3esNePtnPVwD-VweYNoRQGYxIm. [本文引用:1]
[19]	陈黎卿, 林建飞, 汤池潜, 等. 电控空气悬架系统参数的多目标优化[J]. 机械科学与技术, 2017, 36(3): 462-468. Chen Li-qing, Lin Jian-fei, Tang Chi-qian, et al. Multi-objective optimization on parameters of electronically controlled air suspension system[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(3): 462-468. [本文引用:1]

2002

0.0

... 0 引言现有的空气弹簧模型主要有简单模型、Nishimura、VAMPIRE、SIMPACK、GENSYS等5种模型^[1],适用于汽车产品预开发阶段的仿真匹配,需要试验数据做大量的参数辨识,国内外学者基于以上几种模型对空气弹簧的动力学行为及影响因素进行了大量研究^[2,3,4],取得了丰硕的研究成果 ...

2008

0.0

2011

0.0

2015

0.0

2011

0.0

... 大多数学者在对空气弹簧的特性研究中关于有限元分析^[5,6,7]的方法较多,能较为准确地分析空气弹簧气囊的受力,但此类方法需要建立复杂的有限元模型,且分析过程耗时较长 ...

2014

0.0

2011

0.0

. 2011, 2011(2):10-13 DOI:doi:10.3969/j.issn.1000-3703.2011.02.003

Study on the influence of cord parameters on the vertical stiffness of air springs for vehicles based on ABAQUS

ABAQUS 的帘线参数对汽车空气弹簧垂向刚度影响的研究

Tu De-xin , Huang Chang-wen , Chen Mao-quan

屠德新, 黄昌文, 陈毛权, . 基于

运用非线性有限元分析软件ABAQUS建立膜式空气弹簧有限元模型,计算其垂向刚度特性,讨论帘线角、帘线层间距、帘线层数等安全气囊帘线参数对空气弹簧垂向刚度特性的影响.将0.3 MPa和0.5 MPa空气弹簧垂向刚度曲线与试验曲线进行了比较,结果表明,计算值与试验值比较吻合,证明该模型正确,仿真结果有效.

2013

0.0

... 也有采用拟合试验数据^[8,9,10]的方法,在整车动力学仿真匹配时可以通过插值计算得到空气弹簧悬架刚度,此类方法适合验证空气弹簧建模分析方法的准确性,但不能预测空气弹簧动特性 ...

2010

0.0

. 2010, 46(4):93-98

Dynamic characteristics fitting of springs and numerical analysis of air suspensions with variant stiffness

空气弹簧动态特性拟合及空气悬架变刚度计算分析

Chen Liao , Zhou Kong-kang , Li Zhong-xing.

陈燎, 周孔亢, 李仲兴

2014

0.0

. 2014, 34(3):166-170 DOI:doi:10.3969/j.issn.1674-3261.2014.03.008

Test study of character of adjustable stiffness of diaphragm air springs

可调刚度膜式空气弹簧特性试验研究

Chen Shuang , Zong Chang-fu , Sun Yan

陈双, 宗长富, 孙艳

以某种膜式空气弹簧为研究对象，在分析空气弹簧特点及工作原理基础上，建立空气弹簧特性试验系统，完成空气弹簧刚度特性实验和电磁阀充放气实验。通过一定弹簧高度下气囊内部气体的充放气实验，了解电磁阀开关时间与弹簧内部气体压力的关系；通过对空气弹簧进行斜坡信号加载实验，了解一定初始压力下空气弹簧有效面积变化、有效容积变化和弹簧刚度变化。试验结果将为基于电控空气悬架的汽车平顺性控制研究奠定基础。

2004

0.0

. 2004, 27(10):1191-1195 DOI:doi:10.3969/j.issn.1003-5060.2004.10.021

Analysis and calculation of diaphragm air spring of an automobile

汽车膜式空气弹簧的分析与计算

Li Bin , Chen Wu-wei.

李滨, 陈无畏

对空气弹簧悬架中的主要元件膜式空气弹簧进行了分析,在简化计算模型的基础上,进行空气弹簧系统垂直刚度及振动频率的计算和结果分析.在膜式空气弹簧结构与计算模型的基础上,建立起膜式空气弹簧有效面积、有效面积的变化率及有效体积变化率的计算模型.通过实例分析与空气弹簧的负荷特性计算,对空气弹簧的设计与计算提供了理论依据.

... 现有的基于结构的理论分析^[11,12,13]方法中,大多数学者或多或少地忽略了空气弹簧的活塞结构,而实际上空气弹簧活塞形状对空气弹簧动刚度影响很大,其由锥面、柱面和弧面中的一种或多种组合而成,因此有必要基于活塞实际形状对空气弹簧进行特性分析 ...

... 33^[11] ...

2014

0.0

. 2014, 50(24):137-144

Analysis of stiffness characteristics and influencing factors based on single chamber cross-section air spring

单气室变截面空气弹簧刚度特性及影响因素分析

Tang Chuan-yin , Zhang Yi-min , Li Yun-gong

唐传茵, 张义民, 李允公

2012

0.0

. 2012, 29(1):331-334 DOI:doi:10.3969/j.issn.1006-9348.2012.01.084

Simulation of stiffness character of diaphragm air spring based on change piston contour

基于活塞形状改变的空气弹簧特性仿真研究

Hu De-an , Gan Liang-liang , Ding Fei

胡德安, 甘亮亮, 丁飞

摘　要：研究汽车装用空气弹簧刚度优化问题，活塞形状对膜式空气弹簧刚度特性的影响较大。为了提高整车的平顺性能．建立空气弹簧简化模型，得到圆台和倒圆台活塞形状下空气弹簧的有效承载半径影响因素。利用ABAQUS软件建立安装圆柱、圆台和倒圆台活塞的空气弹簧有限元模型进行，研究了不同圆台角下圆台活塞空气弹簧的刚度特性。仿真结果表明，在一定范围内，圆台角度越大，空气弹簧剐度也越大，证明与理论分析吻合，并对空气弹簧的设计和匹配具有一定的指导意义。

2009

0.0

. 2009, 39(5):1125-1129

Matching and optimization of heavy commercial vehicle cab air suspension system

重型商用车驾驶室空气悬置系统的匹配优化

Chen Jing , Cao Xiao-lin , Wang Deng-feng

陈静, 曹晓琳, 王登峰

A rigid multibody dynamic model was built for the heavy commercial vehicle cab air suspension system using the virtual prototype technique. The model was verified by the vehicle road test, and used to analyze the modal characteristics and the ride comfort of the vehicle. Taking the stiffness and the damp of the cab suspension components as test factors, the parameters of the cab suspension system were matched and optimized by means of the orthogonal test design technique. The simulation results indicate that the ride comfort in the cab can be improved by optimization of the cab suspension system parameters.

采用虚拟样机技术建立了重型商用车驾驶室空气悬置多刚体动力学仿真模型，通过道路试验对仿真模型进行了验证，分析了其模态特性及乘坐舒适性。以驾驶室悬置元件刚度、阻尼为因子，运用正交试验技术对驾驶室悬置系统参数进行了匹配优化，结果表明，采用优化后的驾驶室空气悬置参数可使驾驶室的乘坐舒适性有一定程度的提高。

... 在目前公开发表的论文中,大多数学者主要以汽车平顺性为目标对空气悬架的刚度、阻尼进行优化匹配^{[14,15,16,17]},通过电控系统控制空气弹簧的内压,从而调节空气弹簧的刚度,很少有人进一步地对空气弹簧结构设计参数进行优化 ...

2009

0.0

. 2009, 16(03):182-186 DOI:doi:10.3785/j.issn.1006-754X.2009.03.005

Optimization of air suspension parameters based on multi-body dynamic

基于多体力学的汽车空气弹簧悬架优化

Jiang Sheng , Qing Qi-xiang , Long Lyu-bo.

姜圣, 卿启湘, 龙铝波

基于 ADAMS/View软件对湖南大学自主研发的某一车型,以提高整车行驶平顺性为目的,综合考虑阻尼系数、悬架刚度和非簧载质量各因素对平顺性的影响,建立了空气弹簧悬架及整车仿真分析模型,构造了仿真分析所需路谱的高程样本,对其影响汽车安全性、平稳性、舒适性的参数进行敏感性分析,并在此基础上对空气弹簧悬架系统参数进行优化设计.通过实车道路试验和仿真结果的对比,验证了仿真的可信度及可行性.

2009

0.0

. , 2014(3):53-57 DOI:doi:10.3969/j.issn.1673-162X.2014.03.013

Heavy tractor matching air suspension parameters optimization

重型牵引车空气悬架参数匹配优化

Xu Qiang , Luo Han-feng , Li Liang.

徐强, 骆汉丰, 李亮

摘　要：在分析空气弹簧刚度特性的基础上,获取空气弹簧动特性曲线优化方法,利用ADAMS/Car 建立重型牵引车空气悬架以及整车虚拟样机模型,以空气弹簧刚度和减振器阻尼为试验因子,以驾驶员处的加权加速度均方根值函数为目标函数,通过响应曲面法建立目标函数与试验因子之间的关系表达式,获取最优空气弹簧动特性曲线.将优化的空气悬架参数代入到整车模型进行分析,仿真结果表明采用优化后的悬架参数可使驾驶员舒适度得到提高.

0.0

... 1 空气弹簧动态特性理论分析基于前进牌橡胶空气弹簧662 N^[18],考虑活塞弧面的膜式空气弹簧的计算模型如图1所示 ...

2017

0.0

. 2017, 36(3):462-468 DOI:doi:10.13433/j.cnki.1003-8728.2017.0322

Multi-objective optimization on parameters of electronically controlled air suspension system

电控空气悬架系统参数的多目标优化

Chen Li-qing , Lin Jian-fei , Tang Chi-qian

陈黎卿, 林建飞, 汤池潜

摘　要：针对传统悬架将结构参数与控制参数分开设计,易造成系统失去全局最优的不足,本文以电子控制空气悬架为例提出一种对其结构/控制参数多目标优化的方法。首先建立了带附加气室空气弹簧和电磁阀式减振器空气悬架数学模型,运用台架试验的方法验证了所建模型的精度。设计了LQR控制器对减振器阻尼力控制,选取带附加气室空气弹簧节流孔尺寸作为优化结构参数,控制器与振动加速度有关的权系数作为优化的控制参数,运用多种群遗传算法分别对系统结构/控制参数多目标优化,控制参数优化,结构参数优化。优化结果显示,相对于系统结构参数与控制参数分开优化,悬架系统结构/控制参数多目标优化后系统性能得到进一步提升。