Burckhardt等^[9]通过大量试验提出了一个轮胎-路面数学模型, 可以较准确地描述轮胎与路面之间的非线性纵向附着特性, 其表达式为:

μ =c₁ 1-e-c2s-c₃s(1)

式中:c₁、c₂、c₃为典型路面的参数值。

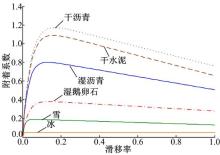
图1为Burckhardt轮胎模型中6种典型路面的附着系数-滑移率曲线。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 典型路面的μ -s曲线Fig.1 Typical road μ -s curve

从图1可以看出, 不同路面的附着系数-滑移率曲线都非常相似, 其非线性变化的趋势和规律基本相同, 即附着系数都是随着滑移率的增加从零增加到峰值附着系数, 然后再缓慢减小到滑动附着系数, 所以可以认为附着系数-滑移率曲线是每种路面的固有特性, 可将它作为路面识别的重要依据。

基于路面的附着系数曲线相似的固有特性, 定义无量纲特征值τ 表征目标路面与已知路面的相似度。认为目标路面与相近的两条路面都具有一定的相似性, 且满足τ ₁+τ ₂=1, 因此, 目标路面的峰值附着系数可以表示为:

μ _max=τ ₁· μ _1max+τ ₂· μ _2max(2)

式中:τ ₁、τ ₂为目标路面与相近两条路面的相似度; μ _1max、μ _2max为相近两条路面的峰值附着系数。

τ 的定义如下:

τ ₁= φ-φ2φ1-φ2, τ ₂= φ1-φφ1-φ2 (3)

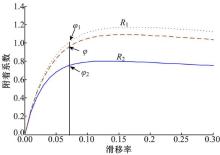
式中:φ 为当前路面的利用附着系数; φ ₁、φ ₂分别为所选两条路面的利用附着系数。

所选两条路面为已知6条路面中与目标路面相邻的两条路面, 且满足如图2所示要求, φ1min> φ > φ2max。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 相似路面的μ -s曲线Fig.2 Similar road μ -s curve

车轮滑移率s和利用附着系数φ 的定义分别为:

s= v-wrv (4)

φ = FXFZ (5)

φ _{1, 2}=c₁ 1-e-c2s-c₃s (6)

式中:v为车轮中心的速度; r为车轮半径; w为车轮的角速度; F_X为地面对车轮的纵向力; F_Z为车轮垂直载荷。

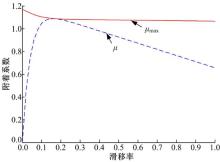
为了验证算法的有效性, 首先利用该算法辨识干水泥路面的峰值附着系数。其中, 滑移率s采用斜率为0.1的递增信号, Burckhardt轮胎模型产生路面信号, 实时输出路面利用附着系数φ 。图3为干水泥路面辨识结果。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 干水泥路面辨识结果Fig.3 Result of dry cement road identification

由图3可以看出, 在滑移率为0~2%期间, 由于滑移率较低, 识别结果与干沥青路面较为相似, 峰值附着系数辨识结果为[1.17, 1.09], 在其余滑移率(2%~100%)下, 辨识效果较好, 峰值附着系数辨识结果为[1.09~1.07], 与设定的几乎一致, 误差在2%以内。结果表明, 该算法辨识效果较好, 精度较高。且滑移率从0~1的辨识结果一致性较好, 最大误差在0.08以内, 充分证明了算法精度较高。

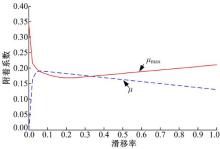
为了进一步验证算法的适用性, 再次利用辨识算法计算雪路面的峰值附着系数。同样, 滑移率s采用斜率为0.1的递增信号, Burckhardt轮胎模型产生路面信号。图4为雪路面辨识结果。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 雪路面辨识结果Fig.4 Result of snow road identification

由图4可以看出, 在滑移率为0~2%时, 由于滑移率较低, 识别结果与湿鹅卵石路面较为相似, 峰值附着系数辨识结果较大。在滑移率为5%~15%时, 辨识算法准确识别出路面为雪路面, 峰值附着系数辨识结果范围为[0.20, 0.18], 误差在5%左右。滑移率在20%~100%范围内, 当峰值附着系数辨识结果在滑移率为20%时, 最小为0.175, 在滑移率为100%时, 最大为0.21, 与设定的雪路面峰值附着系数0.19基本一致, 满足要求。结果表明, 该辨识算法在较差路面同样具有较高的精度。

制动减速度是制动时车速对时间的导数, 即dv/dt。它反映了地面制动力的大小^[10]。

在不同路面上, 由于地面制动力为:

F_Xb=φ _b· G(7)

故汽车能达到的减速度为:

a_bmax=φ _b· g(8)

若装有理想的制动防抱死装置来控制汽车的制动, 使车轮制动力达到地面制动力极限, 则制动减速度为:

a_bmax=φ _p· g(9)

式中:F_Xb为地面制动力; φ _b为制动力系数; G为汽车重力; g为重力加速度; φ _p为路面峰值附着系数。

本文主要分析针对不同路面获得的最大制动减速度, 通过路面辨识获得路面峰值附着系数, 所以期望制动减速度为:

a_des=μ _max· g(10)

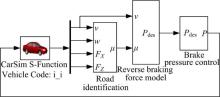
在制动时, 被控车辆处于直线行驶状态, 因此, 考虑建立被控车辆沿其前进方向的制动动力学模型。在制动时, 逆制动力模型根据期望加速度和车速计算出期望制动压力。

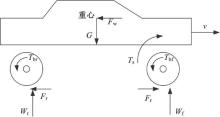
根据车辆受力分析图5, 其中, v为车速, F_w为空气阻力, T_s为驱动力矩, T_bf、T_br分别为前轮和后轮的制动力矩, F_f和F_r分别为地面作用于前、后轮的切向力, W_f和 W_r分别为前、后轮的垂直载荷。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 车辆受力分析图Fig.5 Force analysis of vehicle

忽略车辆旋转部件的质量换算, 将车辆运动方程表示如下:

ma_des=F_t-F_Xb-∑ F(v) (11)

式中:F_t为驱动力; F_Xb为制动力; ∑ F(v)为各种阻力的总和, 本文简化∑ F(v), 只取其风阻值和滚动阻力, 即:

∑ F=C_DA_aρ v²+mgf (12)

式中:C_D为空气阻力系数; A_a为迎风面积; f为滚动阻力系数; ρ 为空气密度。

由式(11)和式(12)可得期望制动力计算及逆制动模型为:

P_des= |mades+12CDAaρv2+mgf|Kb (13)

式中:P_des为期望制动压力; K_b为比例系数。

制动压力控制器旨在实时控制轮缸制动压力, 使其达到期望制动压力值, 从而实现汽车的主动制动^[11]。因此, 压力控制器要求快速达到目标值并且尽量消除超调和静差。常规PID对于线性定常系统的控制非常有效, 但对于汽车制动这种非线性、时变的复杂系统, 因其PID参数不是整定困难就是无法整定, 因而很难达到预期的控制效果。单神经元作为构成神经网络的基本单位, 具有自学习和自适应能力, 且结构简单而易于计算。相较于传统PID, 单神经元PID对非线性时变复杂系统的适应性更好, 而且可以自整定控制参数, 省去了繁琐的参数整定环节, 所以本文采用单神经元PID控制策略设计制动压力控制器。

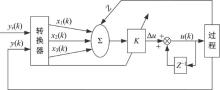
单神经元PID控制器的基本结构如图6所示。将期望制动压力P_des与实际制动压力P的差值作为单神经元PID控制器的输入, 采用有监督的Hebb学习规则后, 可实现PID参数的在线自整定, 且能保证系统的鲁棒性。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 单神经元PID控制器结构图Fig.6 Structure diagram of single neuron PID controller

制动压力控制算法如下:

ΔP(k)=ΔP(k-1)+K∑3i=1wi(k)xi(k)wi=wi(k)/∑i=13wi(k)w1(k+1)=w1(k)+ηIz(k)u(k)e(k)+Δe(k)w2(k+1)=w2(k)+ηPz(k)u(k)e(k)+Δe(k)w3(k+1)=w3(k)+ηDz(k)u(k)e(k)+Δe(k) (14)

式中:Δ P为期望制动压力与实际制动压力差值。η _I、η _P、η _D分别为积分、比例、微分的学习速率; K为神经元的比例系数; w_i(k)为对应于状态量x_i(k)的加权系数; u(k)为输出值; e(k)为偏差值; Δ e(k)为偏差值的差值。

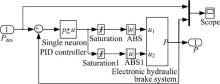
在Simulink中搭建如图7所示的制动压力控制仿真模型。由于本文所建制动系统主要是实现主动避撞系统中主动制动的功能, 故只针对基本制动功能进行仿真验证, 即验证制动压力响应效果。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 制动压力控制仿真模型Fig.7 Simulation model of brake pressure control

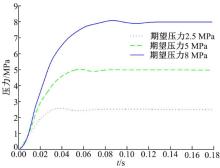
分别设定期望制动压力为2.5、5、8 MPa, 系统响应结果如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 目标压力响应图Fig.8 Target pressure response diagram

由图8可见, 目标压力为8 MPa时, 系统响应时间为0.12 s左右, 且调节过程超调量较小, 基本没有稳态静差。传统液压制动系统制动时, 驾驶员全力踩下制动踏板, 轮缸压力最快响应时间一般为0.2~0.9 s, 由仿真结果可以看出, 目标压力为2.5 MPa时, 系统可以在0.07 s内响应, 目标压力为5 MPa时, 系统也在0.08 s内达到预设压力, 由此可以看出本文所建制动压力控制器可以满足主动制动需求, 且制动过程中有较好的动态和稳态效果。

针对于路面实变的特性, 要求压力控制器能实时达到期望压力, 所以进行增、减压的仿真, 验证其控制效果, 并与PID控制进行对比。

由图9可以看出, 单神经元PID控制下压力从0增加到4 MPa仅需0.06 s, 超调量约为2.1%, 几乎没有静差; 在减压工况, 响应时间约为0.35 s, 静差可以忽略不计。仿真结果表明, 相较于PID控制, 单神经元PID压力控制器有更快的响应时间, 较小的超调量, 并能保证基本无静差。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 压力控制对比图Fig.9 Comparison of pressure control

结果表明, PID控制较为简单易用, 且响应速度可以达到主动避撞系统要求, 但调节过程中有较大的震荡且有一定的稳态静差。相较而言, 单神经元PID控制不仅有较快的响应速度, 而且可以保证系统的鲁棒性, 拥有较好的动态和稳态效果。

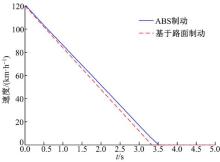
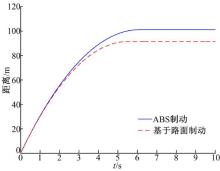
在CarSim中设置路面摩擦因数为0.85, 相当于干水泥路面, 设置车辆行驶工况:初速度为120 km/h, 给ABS制动车辆设置10 MPa的制动压力, 使其实现最大强度制动。图11、图12为仿真结果。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 速度-时间曲线Fig.11 Velocity-time curve

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 距离-时间曲线Fig.12 Distance-time curve

由图11、图12可知, 从120 km/h到完全停止, R车用时3.3 s, 制动减速度为10.1 m/s², 制动距离为55.4 m; B车用时3.5 s, 制动减速度为9.5 m/s², 制动距离为58.5 m。结果表明, 基于路面的最大制动力R车比ABS的B车制动时间减少了5.7%, 制动减速度提高了6.3%, 制动距离缩短了5.3%。

在CarSim中设置路面摩擦因数为0.5, 路面水平相当于比湿沥青路面差一点, 设置同样的车辆行驶工况:初速度为120 km/h, 给ABS制动车辆设置10 MPa的制动压力, 使其实现最大强度制动。图13、图14为仿真结果。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 速度-时间曲线Fig.13 Velocity-time curve

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 距离-时间曲线Fig.14 Distance-time curve

由图13、图14可知, 从120 km/h到完全停止, R车用时5.5 s, 制动减速度为6.06 m/s², 制动距离为91 m; B车用时6.1 s, 制动减速度为5.46 m/s², 制动距离为101 m。结果表明, 基于路面的最大制动力R车比ABS的B车制动时间减少了9.8%, 制动减速度提高了11%, 制动距离缩短了9.9%。

通过对比可以发现, 随着路面附着条件的降低, R车相较于B车制动性能提高越来越明显, 这是因为在附着条件较差的路面, 最佳滑移率在10%左右, 甚至以下, 而ABS仍然将滑移率控制在10%~20%, 所以路面条件越差, ABS制动时偏移最佳滑移率越多, 制动性能下降越明显。

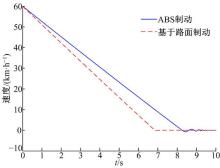
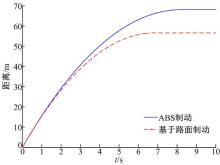
在CarSim中设置路面摩擦因数为0.2, 路面条件相当于比雪路面好一点, 为了切合实际, 设置车辆行驶工况:初速度为60 km/h, 同样给ABS制动车辆设置10 MPa的制动压力, 使其实现最大强度制动。图15~图17为仿真结果。

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 速度-时间曲线Fig.15 Velocity-time curve

图16

Fig.16

	Figure Option ViewDownloadNew Window
	图16 距离-时间曲线Fig.16 Distance-time curve

图17

Fig.17

	Figure Option ViewDownloadNew Window
	图17 质心轨迹Fig.17 Centroid trajectory

由图15、图16可知, 从60 km/h到完全停止, R车用时6.85 s, 制动减速度为2.4 m/s², 制动距离为56.6 m; B车用时8.25 s, 制动减速度为2 m/s², 制动距离为68.1 m。结果表明, 基于路面的最大制动力R车比ABS的B车制动时间减少了17%, 制动减速度提高了20%, 制动距离缩短了16.9%。

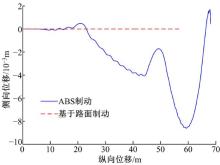
图17为两车制动时的质心轨迹, 可以看出R车制动时方向稳定性较好, 并未发生侧滑; B车发生轻微侧滑, 是因为在较差路面, ABS通过控制轮缸压力增压减压, 将四轮滑移率持续控制在10%~20%, 由于延迟滞后现象, 造成轻微侧滑, 最大侧向位移为0.008 m, 也可以忽略不计。而R车只需保压, 所以不会出现侧滑现象。