双半挂汽车列车转弯运动轨迹仿真分析

引用本文

王郭俊, 许洪国, 刘宏飞. 双半挂汽车列车转弯运动轨迹仿真分析. 2018, 48(2): 415-422
WANG Guo-jun, XU Hong-guo, LIU Hong-fei. Simulation analysis of turning trajectory of B-double vehicles. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 415-422 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170192
Permissions

双半挂汽车列车转弯运动轨迹仿真分析

王郭俊, 许洪国, 刘宏飞

吉林大学交通学院, 长春 130022

通信作者:刘宏飞(1971-),男,博士,副教授. 研究方向:半挂汽车列车操纵稳定性. E-mail:hongfeiliu@jlu.edu.cn

作者简介:王郭俊(1990-),男,博士研究生. 研究方向:多挂汽车列车动力学仿真. E-mail:wangguoyl@qq.com

基金项目:国家自然科学基金项目(51475199); 运输车辆运行安全技术交通运输行业重点实验室开放课题项目(KFKT2016-01)

摘要

建立了双半挂汽车列车的运动学模型,给出了其转弯运动轨迹的一种求解方法,并用MATLAB软件仿真得到各个车辆单元,包括牵引车前轴和后轴、第一节半挂车后轴和第二节半挂车后轴转弯运动的轨迹。最后通过不同结构参数包括半挂车轴距和铰接点位置的设定,对比分析了各轴中点运动轨迹的变化;研究结果表明,对半挂车后轴进行主动转向控制,能有效改善双半挂汽车列车的转向灵活性和运行稳定性。

关键词: 车辆工程; 双半挂汽车列车; 转弯; 轨迹; 主动转向

中图分类号:U469.54 文献标志码:A 文章编号:1671-5497(2018)02-0415-08

Simulation analysis of turning trajectory of B-double vehicles

WANG Guo-jun, XU Hong-guo, LIU Hong-fei

College of Transportation, Jilin University, Changchun 130022,China

Abstract

The kinematics model and solving algorithm of turning trajectory of B-double vehicles are proposed. The trajectories of the front and rear axles of the tractor, the rear axle of the first semitrailer and the rear axle of the second semitrailer are simulated using MATLAB. By changing the structurla parameters including the wheel base of the semitrailers and the position of the articulated point, comparative analysis of the trajectory of each axle center is carried out. Results show that by control of the corner of rear axle of the semitrailer, the handling stability and the flexible steering of B-double vehicles can be improved.

Key words: vehicle engineering; B-double vehicles; turning; trajectory; active steering

Show Figures

0 引言

国外汽车列车在大型物流运输中扮演着至关重要的角色。双半挂汽车列车运输形式, 可有效提高运输效率, 减少燃油消耗, 具有较好的经济效益。目前, 国内大宗货物运输普遍以半挂汽车列车运输为主。在新修订的GB1589-2016中, 半挂车的许用长度由13 m变为13.75 m, 取消了整体封闭式厢式半挂车、低平板半挂车和集装箱半挂车的长度限制特例, 尤其新增了车型品种, 包括中置轴车辆运输车及其列车、中置轴货运挂车及其列车和长头铰接列车等^[1]。因此, 研究双半挂汽车列车在转弯运动过程中的轨迹特性, 对我国物流及道路运输的未来发展有重要意义。

裴金^[2]改进了牵引车前轮轨迹在牵引车坐标系中迁移的数学模型, 提出了半挂车后轮转角的一种控制方式, 使之能够适用于任意弯道, 使半挂车后轴中点能完全跟踪牵引车前轴中点的轨迹; 对各种外部干扰引起的误差予以自动矫正, 并通过仿真分析验证了其理论。郑旺辉^[3]在半挂车后轮转向原理的基础上, 给出了汽车折角、牵引车和半挂车的轨迹偏差计算方法和公式; 以试验样车为例, 提出了减小这种运动轨迹偏差的方法。林熊熊^{[4, 5]}通过建立半挂和全挂汽车转弯模型, 并引申出汽车全轮转向运动轨迹的一种算法, 进而给出了一种统一解法。许言等^[6]基于半挂汽车列车的弯路转向理论, 提出了半挂车后轮弯路行驶轨迹跟踪模型, 并通过SIMULINK仿真验证了汽车列车模型的正确性。王新建等^[7]提出了通过一种控制汽车列车折角的方法, 使得汽车列车具有良好的轨迹跟踪性。Nayl 等^[8]研究了在不同速度和质心侧偏角的情况下, 运动学模型转化为容错性动力学模型, 用模型预测控制器实现汽车列车的轨迹跟踪问题。Jujnovich等^[9]构建了重型汽车列车的运动学模型, 在低速和高速情况下运用非线性控制器使挂车主动转向, 实现轨迹跟踪问题。游峰等^[10]建立了欠驱动汽车列车动力学模型, 应用滑模变结构理论给出了车辆系统状态变量向超平面收敛的方法, 对平滑运动轨迹和小曲率转弯半径的轨迹有良好的跟踪能力。段斌等^[11]根据国标中对外摆值的定义、限值和实验测试方法, 对外摆值的数值计算方法进行了研究, 利用TruckSim仿真和实车试验对此算法进行了验证, 为半挂汽车列车的通过性研究提供了一种思路。刘朝涛^[12]通过ADAMS建立了具有两节全挂车的汽车列车的运动学和动力学模型, 建立了列车的转向控制MATLAB模型, 通过联合仿真对主动转向汽车列车的可行性、优越性进行了验证。龙佳庆等^[13]建立了半挂汽车列车TruckSim模型; 仿真结果表明, 适当增加牵引车的质量, 加长牵引车轴距、加长半挂车轴与牵引车前轴的距离、降低挂车质量、缩短铰接点到牵引车前轴的距离, 会增加不足转向特性的趋势。

目前, 国内外多数研究半挂汽车列车的运行轨迹及其跟踪问题, 包括通过运动学模型和动力学模型来求解轨迹; 少数研究了多挂汽车列车轨迹, 但主要通过汽车动力学软件直接进行求解和验证, 鲜有讨论挂车后轴主动转向对汽车列车行驶轨迹的影响。双半挂汽车列车车辆单元多, 车身长, 在转弯运动中存在后部放大效应, 轨迹跟踪性较差, 通道圆增大。为了仿真实时转弯运动轨迹, 本文通过构建汽车列车运动学模型, 改变车辆参数和控制半挂车后轴主动转向, 改善汽车列车转向灵活性和行驶稳定性, 并对其轨迹的影响进行了研究。

1 双半挂汽车列车的运动学建模

假定双半挂汽车列车低速运行, 3个车辆单元运行在同一平面上, 轮胎侧偏特性在线性范围内变化。为便于对其运动学性能进行研究, 可忽略路面不平度、转向系、轮胎侧偏、车身侧倾等因素, 将左右两侧轮胎简化为集中到车身中轴线的一个轮胎, 形成双半挂汽车列车的单轨模型, 如图1所示。

	Figure Option View Download New Window
	图1 双半挂汽车列车运动学模型Fig.1 Kinematics model of B-double vehicles

3个车辆单元可简化为3个不计质量的AB、CD和EF。A、B、C分别为牵引车前轴的中点、后轴的中点和铰接点, D和E分别为第一节半挂车后轴的中点和铰接点, F为第二节半挂车后轴的中点。其中, D和F为受控点, 可分别控制两节半挂车后轴轮胎的转向角度。AB和A₁B₁为牵引车当前时刻和下一时刻的位置, CD和C₁D₁为第一节半挂车当前时刻和下一时刻的位置, EF和E₁F₁为第二节半挂车当前时刻和下一时刻的位置。其中A点坐标为(x₁, y₁), 极径为OA(OA₁), B点坐标为(x₂, y₂), 极径为OB(OB₁), C点坐标为(x₃, y₃), 极径为OC(OC₁), D点坐标为(x₄, y₄), 极径为OD(OD₁), E点坐标为(x₅, y₅), 极径为OE(OE₁), F点坐标为(x₆, y₆), 极径为OF(OF₁)。

2 汽车列车转弯轨迹的求解过程

采用直角坐标和极坐标相结合的计算方法, 预设步长, 每迭代一次可求出各个车辆单元对应各点的新坐标, 运行结束便可求出车辆转弯运动轨迹。

2.1 B点坐标计算

根据几何关系, 有

$\begin{matrix} \frac{O B_{1}}{\sin ∠ B_{1} BO} \end{matrix}$ = $\begin{matrix} \frac{OB}{\sin (π - ∠ B_{1} OB - ∠ B_{1} BO)} \end{matrix}$ (1)

OB₁= $\begin{matrix} \frac{OBsin ∠ B_{1} BO}{\sin (∠ B_{1} OB + ∠ B_{1} BO)} \end{matrix}$ (2)

根据极限定义, 有

OB₁= $\begin{matrix} \lim_{∠ B_{1} OB \to 0} \end{matrix} \begin{matrix} \frac{[\frac{OBsin ∠ B_{1} BO}{\sin (∠ B_{1} OB + ∠ B_{1} BO)} - OB]}{∠ B_{1} OB} \end{matrix}$ =- $\begin{matrix} \frac{OB}{\tan ∠ B_{1} BO} \end{matrix}$ (3)

∠B₁OB很小时, ∠B₁BO≈ ∠ABO, 故视其为常量。此时B₁点的极径为

OB₁=OB· exp $\begin{matrix} (- \frac{∠ BO B_{1}}{\tan ∠ ABO}) \end{matrix}$ (4)

B₁点坐标的表达式为:

$\begin{matrix} \{\begin{matrix} x_{2} = O B_{1} \cos ∠ B_{1} Ox \\ y_{2} = O B_{1} \sin ∠ B_{1} Ox \end{matrix} \end{matrix}$ (5)

2.2 A点坐标计算

A点为牵引车前轴的中点, 控制着双半挂汽车列车的运行路径。设A运行轨迹的半径为R, 则A点的极径为OA₁=OA=R。

∠A₁OB₁=arccos $\begin{matrix} \frac{O A_{1}^{2} + O B_{1}^{2} - A_{1} B_{1}^{2}}{2 \cdot O A_{1} \cdot O B_{1}} \end{matrix}$ (6)

导出A₁点的极角为:

∠A₁Ox=∠B₁Ox+∠A₁OB₁(7)

A₁点坐标的表达式为:

$\begin{matrix} \{\begin{matrix} x_{1} = O A_{1} \cos ∠ A_{1} Ox \\ y_{1} = O A_{1} \sin ∠ A_{1} Ox \end{matrix} \end{matrix}$ (8)

牵引车分别以90° 、180° 、270° 和360° 驶出弯道, A₁的终点坐标表达式分别为:

$\begin{matrix} \{\begin{matrix} x_{1} = x_{2} - \sqrt[]{A B^{2} - (B - y_{2})^{2}} \\ y_{1} = R \\ O A_{1} = \sqrt[]{x_{1}^{2} + R^{2}} \end{matrix} \end{matrix}$ (9)

$\begin{matrix} \{\begin{matrix} x_{1} = - R \\ y_{1} = y_{2} - \sqrt[]{A B^{2} - (R + x_{2})^{2}} \\ O A_{1} = \sqrt[]{y_{1}^{2} + R^{2}} \end{matrix} \end{matrix}$ (10)

$\begin{matrix} \{\begin{matrix} x_{1} = x_{2} + \sqrt[]{A B^{2} - (R + y_{2})^{2}} \\ y_{1} = - R \\ O A_{1} = \sqrt[]{x_{1}^{2} + R^{2}} \end{matrix} \end{matrix}$ (11)

$\begin{matrix} \{\begin{matrix} x_{1} = R \\ y_{1} = y_{2} + \sqrt[]{A B^{2} - (R - x_{2})^{2}} \\ O A_{1} = \sqrt[]{y_{1}^{2} + R^{2}} \end{matrix} \end{matrix}$ (12)

2.3 C点坐标计算

根据几何关系, 有:

∠A₁B₁O=arccos $\begin{matrix} \frac{A_{1} B_{1}^{2} + O B_{1}^{2} - O A_{1}^{2}}{2 \cdot A_{1} B_{1} \cdot O B_{1}} \end{matrix}$ (13)

OC₁= $\begin{matrix} \sqrt[]{O B_{1}^{2} + C_{1} B_{1}^{2} - 2 \cdot O B_{1} \cdot C_{1} B_{1} \cos ∠ A_{1} B_{1} O} \end{matrix}$ (14)

∠C₁OB₁=arcsin $\begin{matrix} \frac{C_{1} B_{1} \sin ∠ A_{1} B_{1} O}{O C_{1}} \end{matrix}$ (15)

导出C₁点的极角为:

∠C₁Ox=∠C₁OB₁+∠B₁Ox(16)

C₁点坐标的表达式为:

$\begin{matrix} \{\begin{matrix} x_{3} = O C_{1} \sin ∠ C_{1} Ox \\ y_{3} = O C_{1} \cos ∠ C_{1} Ox \end{matrix} \end{matrix}$ (17)

2.4 D点坐标计算

根据几何关系, 有

∠C₁OD=∠C₁Ox+∠DOx(18)

C₁D= $\begin{matrix} \sqrt[]{O C_{1}^{2} + O D^{2} - 2 \cdot O C_{1} \cdot ODcos ∠ C_{1} OD} \end{matrix}$

(19)

∠C₁DO=arccos $\begin{matrix} \frac{C_{1} D^{2} + O D^{2} - O C_{1}^{2}}{2 \cdot C_{1} D \cdot OD} \end{matrix}$ (20)

∠C₁DC=∠CDO-∠C₁DO=∠CDO-arccos $\begin{matrix} \frac{C_{1} D^{2} + O D^{2} - O C_{1}^{2}}{2 \cdot C_{1} D \cdot OD} \end{matrix}$ (21)

DD₁=C₁Dcos(∠C₁DC+∠CDD₁)- $\begin{matrix} \sqrt[]{C_{1} D_{1}^{2} - {[C_{1} Dsin (∠ C_{1} DC + ∠ CD D_{1})]}^{2}} \end{matrix}$

(22)

OD₁= $\begin{matrix} \sqrt[]{O D^{2} + D D_{1}^{2} - 2 \cdot OD \cdot D D_{1} \cos (∠ CDO + ∠ CD D_{1})} \end{matrix}$

(23)

∠D₁OD=arcsin $\begin{matrix} \frac{\sin (∠ CDO + ∠ CD D_{1})}{O D_{1}} \end{matrix}$ (24)

导出D₁点的极角为:

∠D₁Ox=∠DOx+∠D₁OD(25)

D₁点坐标的表达式为:

$\begin{matrix} \{\begin{matrix} x_{4} = O D_{1} \cos ∠ D_{1} Ox \\ y_{4} = O D_{1} \sin ∠ D_{1} Ox \end{matrix} \end{matrix}$ (26)

∠C₁D₁O=arccos $\begin{matrix} \frac{C_{1} D_{1}^{2} + O D_{1}^{2} - O C_{1}^{2}}{2 \cdot C_{1} D_{1} \cdot O D_{1}} \end{matrix}$ (27)

式(27)中∠C₁D₁O在下一时刻替代式(20)中的∠C₁DO。

2.5 E点坐标计算

根据几何关系, 有:

OE₁= $\begin{matrix} \sqrt[]{O D_{1}^{2} + E_{1} D_{1}^{2} - 2 \cdot O D_{1} \cdot E_{1} D_{1} \cos ∠ C_{1} D_{1} O} \end{matrix}$

(28)

∠E₁OD₁=arcsin $\begin{matrix} \frac{E_{1} D_{1} \sin ∠ C_{1} D_{1} O}{O E_{1}} \end{matrix}$ (29)

导出E₁点的极角为:

∠E₁Ox=∠E₁OD₁+∠D₁Ox(30)

E₁点坐标的表达式为:

$\begin{matrix} \{\begin{matrix} x_{5} = O E_{1} \cos ∠ E_{1} Ox \\ y_{5} = O E_{1} \sin ∠ E_{1} Ox \end{matrix} \end{matrix}$ (31)

2.6 F点坐标计算

∠E₁OF=∠E₁Ox+∠xOF(32)

E₁F= $\begin{matrix} \sqrt[]{O {E_{1}}^{2} + O F^{2} - 2 \cdot O E_{1} \cdot OFcos ∠ E_{1} OF} \end{matrix}$ (33)

∠E₁FO=arccos $\begin{matrix} \frac{E_{1} F^{2} + O F^{2} - O E_{1}^{2}}{2 \cdot E_{1} F \cdot OF} \end{matrix}$ (34)

∠E₁FE=∠EFO-∠E₁FO=∠EFO-arccos $\begin{matrix} \frac{E_{1} F^{2} + O F^{2} - O {E_{1}}^{2}}{2 \cdot E_{1} F \cdot OF} \end{matrix}$ (35)

FF₁=E₁Fcos $\begin{matrix} (∠ E_{1} FE + ∠ EF F_{1}) \end{matrix}$ -

$\begin{matrix} \sqrt[]{E_{1} F_{1}^{2} - {[E_{1} Fsin (∠ E_{1} FE + ∠ EF F_{1})]}^{2}} \end{matrix}$ (36)

OF₁= $\begin{matrix} \sqrt[]{O F^{2} + F F_{1}^{2} - 2 \cdot OF \cdot F F_{1} \cos (∠ EFO + ∠ EF F_{1})} \end{matrix}$

(37)

∠F₁OF=arcsin $\begin{matrix} \frac{F F_{1} \sin (∠ EFO + ∠ EFF)}{O F_{1}} \end{matrix}$ (38)

导出F₁点的极角为:

∠F₁Ox=∠FOx+∠F₁OF(39)

F₁点坐标的表达式为:

$\begin{matrix} \{\begin{matrix} x_{6} = O F_{1} \cos ∠ F_{1} Ox \\ y_{6} = O F_{1} \sin ∠ F_{1} Ox \end{matrix} \end{matrix}$ (40)

∠E₁OF₁=arccos $\begin{matrix} \frac{O F_{1}^{2} + E_{1} F_{1}^{2} - O E_{1}^{2}}{2 \cdot O F_{1} \cdot E_{1} F_{1}} \end{matrix}$ (41)

式(41)中∠E₁F₁O在下一时刻替代式(34)中的∠E₁FO。

2.7 其他参数计算

如图2所示, α 为牵引车坐标系X₁BY₁与大地坐标系XOY的夹角, α ₁为第一节半挂车坐标系X₂DY₂与大地坐标系XOY的夹角, α ₂为第二节半挂车坐标系X₃FY₃与大地坐标系XOY的夹角。θ ₁为牵引车与第一节半挂车的铰接角, 取其锐角值。δ ₁为第一节半挂车后轴轮胎的主动转角, 与θ ₁成正比, 比例系数为K₁。θ ₂为两节半挂车之间的铰接角, 取其锐角值。δ ₂为第二节半挂车后轴轮胎的主动转角, 与θ ₂成正比, 比例系数为K₂。上述各量的计算式为:

$\begin{matrix} \{\begin{matrix} tanα = \arctan \frac{x_{2} - x_{1}}{y_{1} - y_{2}} \\ \tan α_{1} = \arctan \frac{x_{4} - x_{3}}{y_{3} - y_{4}} \\ \tan α_{2} = \arctan \frac{y_{5} - y_{6}}{x_{6} - x_{5}} \\ θ_{1} = \arcsin [\sin (α - α_{1})] \\ δ_{1} = K_{1} θ_{1} \\ θ_{2} = \arcsin [\sin (α_{1} - α_{2})] \\ δ_{2} = K_{2} θ_{2} \end{matrix} \end{matrix}$ (42)

	Figure Option View Download New Window
	图2 三个车辆单元的坐标系Fig.2 Coordinate systems for three vehicle units

3 双半挂汽车列车轨迹仿真及分析

3.1 不同路径下的弯道轨迹仿真结果

根据A点的终点坐标, 上述计算过程有4种驶出弯道的情况, 仿真结果如图3所示。双半挂汽车列车的结构参数^[14], 见表1。

由直线过渡到弯道行驶, B点和D点向圆周内侧偏移, 其轨迹半径小于A点的轨迹半径。F点向圆周外侧偏移, 其轨迹半径大于A点的轨迹半径, 此时F点与A点的轨迹偏差为后摆值。进入弯道后, D点跟随B点的轨迹, F点跟随A点的轨迹, 其中B点和D点的轨迹半径小于A点和F点的轨迹半径。由弯道过渡到直线行驶, F点向圆周内侧偏移, 不再跟随A点, 其轨迹半径减小, 此时F点与A点轨迹的偏差为前摆值。F点轨迹半径驶入弯道时变大, 驶出弯道时减小, 表明存在后部放大效应(RWA)。

	Figure Option View Download New Window
	图3 双半挂汽车列车各轴中点弯道运动轨迹Fig.3 Simulation results for each axle center trajectory of B-double vehicles

表1 双半挂汽车列车结构参数 Table 1 Structural parameters for B-double vehicles

3.2 车辆结构参数对各轴中点轨迹的影响

3.2.1 半挂车轴距的影响

轴距CD和EF的参数变化, 见表2。

表2 半挂车轴距参数变化 Table 2 Wheel base variables of semitrailersm

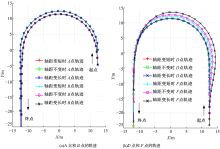
以180° 圆周运动为例, 如图4(a)所示, A点和B点的轨迹不变, A点的轨迹半径比B点大。如图4(b)所示, 轴距CD和EF变短, D点和F点向前偏移。由直线过渡到弯道行驶以及进入弯道后, D点的轨迹变化幅度小, F点向圆周内侧偏移, 外摆值减小。由弯道过渡到直线行驶, D点和F点向圆周外侧偏移, 前摆值减小。轴距CD和EF变长, D点和F点向后偏移。由直线过渡到弯道行驶以及进入弯道后, D点的轨迹变化幅度小, F点向圆周外侧偏移, 外摆值增大。由弯道过渡到直线行驶, D点和F点向圆周内侧偏移, 前摆值增大。D点和F点的轨迹变化趋势相同, 但F点的变化幅度比D点大, 表明存在后部放大效应。

	Figure Option View Download New Window
	图4 半挂车轴距CD、EF变化时的各轴中点轨迹Fig.4 Each axle center trajectory with wheel base variables of semitrailers

3.2.2 铰接点位置的影响

铰接点C和E的位置发生变化^[14], 即CB和ED的长度发生变化, 见表3。

表3 铰接点位置变化 Table 3 Articulated point position variables

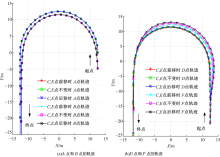
以180° 圆周运动为例, 如图5(a)所示, A点和B点的轨迹不变, A点的轨迹半径比B点大。如图5(b)所示, CB和ED变长, 即C点和E点向前移动时, D点和F点向前偏移。由直线过渡到弯道行驶以及进入弯道后, D点和F点向圆周内侧偏移, 外摆值减小。由弯道过渡到直线行驶, D点和F点的轨迹变化幅度小。CB和ED变短, 即C点和E点向后移动时, D点和F点向后偏移。由直线过渡到弯道行驶以及进入弯道后, D点和F点向圆周外侧偏移, 外摆值增大。由弯道过渡到直线行驶, D点和F点的轨迹变化幅度小。D点和F点的轨迹变化趋势相同, 但F点的变化幅度比D点大, 表明存在后部放大效应。

	Figure Option View Download New Window
	图5 铰接点C、E位置变化时的各轴中点轨迹Fig.5 Each axle center trajectory with articulated point position variables

3.3 半挂车后轴主动转向的影响

低速工况下, 后轴轮胎的主动转角方向与牵引车前轴相反, 以减小转弯半径, 提高转向灵活性。高速工况下, 后轴轮胎的主动转角方向与牵引车前轴相同, 以降低横摆角速度, 提高操纵稳定性^[15]。

以180° 圆周运动为例, 低速工况下, D点和F点主动异向转向, 转向比例系数K₁和K₂取正值。如图6(a)所示, A点和B点的轨迹不变, A点的轨迹半径比B点大。如图6(b)所示, D点和F点向圆周内侧偏移, 轨迹半径变小, 提高了转向灵活性。主动转向比例系数K₁和K₂减小, 轨迹半径减小, 后部放大效应减小。F点的变化幅度比D点大。

以180° 圆周运动为例, 高速工况下, D点和F点主动同向转向, 转向比例系数K₁和K₂取负值。如图7 (a)所示, A点和B点的轨迹不变, A点的轨迹半径比B点大。如图7(b)所示, D点和F点向圆周内侧偏移, 轨迹半径变小, 提高了行驶稳定性。主动转向比例系数K₁和K₂的绝对值增大, 轨迹半径减小, 后部放大效应减小。F点的变化幅度比D点大。

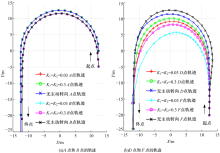	Figure Option View Download New Window
'>	图6 半挂车后轴主动异向转向时的各轴中点轨迹Fig.6 Each axle center trajectory with semitrailers' axles active steering in the opposite direction

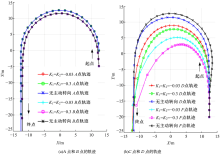	Figure Option View Download New Window
'>	图7 半挂车后轴主动同向转向时的各轴中点轨迹Fig.7 Each axle center trajectory with semitrailers' axles active steering in the same direction

4 结束语

建立了双半挂汽车列车的运动学模型, 采用了直角坐标系和极坐标系相结合的方法, 运用几何定理求解, 对90° 、180° 、270° 和360° 弯道行驶中各轴中点的运动轨迹进行了仿真。结果表明, 在双半挂汽车列车中, 半挂车后轴的轨迹具有跟随性和后部放大效应。半挂车的轴距变化影响其后轴轨迹的变化:轴距越长, 半挂车后轴轨迹向圆周外侧偏移, 轨迹半径增大, 后摆值和前摆值增大; 反之, 轨迹半径减小, 后摆值和前摆值减小。铰接点的位置变化影响半挂车后轴轨迹的变化:铰接点后移, 轨迹向圆周外侧偏移, 轨迹半径增大, 后摆值增大; 反之, 轨迹半径减小, 后摆值减小。半挂车后轴主动转向影响其后轴轨迹的变化:低速工况下半挂车后轴与牵引车前轴轮胎转角方向相反, 高速工况下半挂车后轴与牵引车前轴轮胎转角方向相同, 半挂车后轴轨迹向圆周内侧偏移, 轨迹半径减小, 后部放大效应减小, 提高了转向灵活性和行驶稳定性。文中在分析过程中简化了运动学模型而忽略了一些因素, 在后续的研究中将结合主动转向控制的车辆动力学模型对其轨迹进行仿真, 深入讨论和验证双半挂车列车的轨迹特性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	应朝阳. 国家标准《汽车、挂车及汽车列车外廓尺寸、轴荷及质量限值》(GB1589-2016)制修订情况介绍[J]. 汽车与安全, 2016(8): 90-94. [本文引用:1]
[2]	裴金. 半挂汽车列车弯道同轨迹转向研究及仿真分析[J]. 系统工程与电子技术, 1992(10): 55-60. Pei Jin. Investigation and emulation of vehicle-semitrailer system turning along identical locus curve[J]. Journal of Systems Engineering and Electronics, 1992(10): 55-60. [本文引用:1]
[3]	郑旺辉. 后轮转向半挂汽车列车的轨迹偏差分析[J]. 系统工程与电子技术, 1994(6): 72-80. Zheng Wang-hui. Analysis of track bias of the automobile train with rear wheel steering[J]. Systems Engineering and Electronics, 1994(6): 72-80. [本文引用:1]
[4]	林熊熊. 半挂汽车列车弯路运动轨迹计算机仿真[J]. 汽车工程, 1997(1): 60-65. Lin Xiong-xiong. Computer simulation on trajectory of semi-trailer train on turning path[J]. Automotive Engineering, 1997(1): 60-65. [本文引用:1]
[5]	林熊熊. 全挂汽车列车弯路运动轨迹计算机仿真[J]. 汽车工程, 1997(1): 317-319. Lin Xiong-xiong. Computer simulation on trajectory of full-trailer on turning path[J]. Automotive Engineering, 1997(1): 317-319. [本文引用:1]
[6]	许言, 刘宏飞, 任有, 等. 半挂汽车列车弯路行驶轨迹分析[J]. 长春理工大学学报: 自然科学版, 2008, 31(1): 132-134. Xu Yan, Liu Hong-fei, Ren You, et al. Analysis on the trajectory of the tractor-semitrailer in crook circumstance[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2008, 31(1): 132-134. [本文引用:1]
[7]	王新建, 关志伟. 汽车列车轨迹跟踪性能仿真与模型试验研究[J]. 天津职业技术师范大学学报, 2010, 20(1): 27-29. Wang Xin-jian, Guan Zhi-wei. Platform simulation study on the control of the moving track of tractor-trailer[J]. Journal of Tianjin University of Technology and Education, 2010, 20(1): 27-29. [本文引用:1]
[8]	Nayl T, Nikolakopoulos G, Gustafsson T. Path following for an articulated vehicle based on switching model predictive control under varying speeds and slip angles[C]∥17th-ETFA 2012-IEEE International Conterence on Emerging Technologies & Factory Automation: Krakow, Poland , 2012: 1-7. [本文引用:1]
[9]	Jujnovich B A, Cebon D. Path-following steering control for articulated vehicles[J]. Journal of Dynamic Systems Measurement & Control, 2013, 135(3): 031006. [本文引用:1]
[10]	游峰, 张荣辉, 王海玮, 等. 欠驱动半挂汽车列车的运动建模与跟踪控制[J]. 吉林大学学报: 工学版, 2014, 44(5): 1296-1302. You Feng, Zhang Rong-hui, Wang Hai-wei, et al. Dynamic model and tracking control of tractor semi-trailer vehicle with underactuated system[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1296-1302. [本文引用:1]
[11]	段斌, 单颖春, 刘献栋, 等. 一种半挂汽车列车外摆值的计算方法[J]. 重庆交通大学学报: 自然科学版, 2014, 33(6): 161-166. Duan Bin, Shan Ying-chun, Liu Xian-dong, et al. Out value algorithm of tractor semitrailer combinations[J]. Journal of Chongqing Jiaotong University (Natural Science), 2014, 33(6): 161-166. [本文引用:1]
[12]	刘朝涛, 王永伟, 谭亚红. 基于ADAMS和MATLAB主动转向式汽车列车转向仿真研究[J]. 科技与创新, 2015(10): 9-10. Liu Zhao-tao, Wang Yong-wei, Tan Ya-hong. ADAMS and MATLAB based active steering car train simulation study[J]. Science and Technology & Innovation, 2015(10): 9-10. [本文引用:1]
[13]	龙佳庆, 韦超毅. 基于TruckSim的半挂汽车列车转向特性的仿真分析[J]. 河池学院学报, 2016(2): 79-82. Long Jia-qing, Wei Chao-yi. Simulation analysis of the steering characteristics of semi-dragging trucks based on TruckSim[J]. Journal of Hechi University, 2016(2): 79-82. [本文引用:1]
[14]	交通运输部公路科学研究院等. 公路甩挂运输关键技术[M]. 北京: 人民交通出版社, 2016: 118-128. [本文引用:2]
[15]	张孝祖. 车辆控制理论基础及应用[M]. 北京: 化学工业出版社, 2007: 167-171. [本文引用:1]

0.0

. , 2016(8):90-94

国家标准《汽车、挂车及汽车列车外廓尺寸、轴荷及质量限值》(GB1589-2016)制修订情况介绍

应朝阳

国家标准GB 1589-2016《汽车、挂车及汽车列车外廓尺寸、轴荷及质量限值》已于2016年7月26日发布实施，本文简要介绍了GB 1589-2016的制修订背景、原则、主要修订内容及实施注意事项，以使各级公安机关交通管理部门能及时正确地理解和实施标准相关要求。

... 75 m,取消了整体封闭式厢式半挂车、低平板半挂车和集装箱半挂车的长度限制特例,尤其新增了车型品种,包括中置轴车辆运输车及其列车、中置轴货运挂车及其列车和长头铰接列车等^[1] ...

0.0

. , 1992(10):55-60

Investigation and emulation of vehicle-semitrailer system turning along identical locus curve

半挂汽车列车弯道同轨迹转向研究及仿真分析

Pei Jin.

裴金

... 裴金^[2]改进了牵引车前轮轨迹在牵引车坐标系中迁移的数学模型,提出了半挂车后轮转角的一种控制方式,使之能够适用于任意弯道,使半挂车后轴中点能完全跟踪牵引车前轴中点的轨迹 ...

0.0

. , 1994(6):72-80

Analysis of track bias of the automobile train with rear wheel steering

后轮转向半挂汽车列车的轨迹偏差分析

Zheng Wang-hui.

郑旺辉

本文在介绍半挂车后轮转向原理的基础上，给出了汽车列车的折角、半挂车与牵引车的轨迹偏差的解析计算方法及有关公式。通过对实验样车进行实例计算，提出了减小这种轨迹偏差的方法，得出了一些具有普遍意义的结论。

... 郑旺辉^[3]在半挂车后轮转向原理的基础上,给出了汽车折角、牵引车和半挂车的轨迹偏差计算方法和公式 ...

0.0

. , 1997(1):60-65

Computer simulation on trajectory of semi-trailer train on turning path

半挂汽车列车弯路运动轨迹计算机仿真

Lin Xiong-xiong.

林熊熊

... 林熊熊^[4,5]通过建立半挂和全挂汽车转弯模型,并引申出汽车全轮转向运动轨迹的一种算法,进而给出了一种统一解法 ...

0.0

. , 1997(1):317-319

Computer simulation on trajectory of full-trailer on turning path

全挂汽车列车弯路运动轨迹计算机仿真

Lin Xiong-xiong.

林熊熊

... 林熊熊^[4,5]通过建立半挂和全挂汽车转弯模型,并引申出汽车全轮转向运动轨迹的一种算法,进而给出了一种统一解法 ...

2008

0.0

. 2008, 31(1):132-134 DOI:doi:10.3969/j.issn.1672-9870.2008.01.039

Analysis on the trajectory of the tractor-semitrailer in crook circumstance

半挂汽车列车弯路行驶轨迹分析

Xu Yan , Liu Hong-fei , Ren You

许言, 刘宏飞, 任有

提高半挂汽车列车的轨迹跟踪性,是减小其行驶通道圆,提高转向机动性和主动安全性的有效途径;本文基于半挂汽车列车弯路转向理论,提出了半挂汽车列车后轮弯路行驶轨迹跟踪数学模型,并通过simulink仿真验证了数学模型的正确性.

... 许言等^[6]基于半挂汽车列车的弯路转向理论,提出了半挂车后轮弯路行驶轨迹跟踪模型,并通过SIMULINK仿真验证了汽车列车模型的正确性 ...

2010

0.0

. 2010, 20(1):27-29

Platform simulation study on the control of the moving track of tractor-trailer

汽车列车轨迹跟踪性能仿真与模型试验研究

Wang Xin-jian , Guan Zhi-wei.

王新建, 关志伟

... 王新建等^[7]提出了通过一种控制汽车列车折角的方法,使得汽车列车具有良好的轨迹跟踪性 ...

2012

0.0

... Nayl 等^[8]研究了在不同速度和质心侧偏角的情况下,运动学模型转化为容错性动力学模型,用模型预测控制器实现汽车列车的轨迹跟踪问题 ...

2013

0.0

... Jujnovich等^[9]构建了重型汽车列车的运动学模型,在低速和高速情况下运用非线性控制器使挂车主动转向,实现轨迹跟踪问题 ...

2014

0.0

. 2014, 44(5):1296-1302 DOI:doi:10.7964/jdxbgxb201405012

Dynamic model and tracking control of tractor semi-trailer vehicle with underactuated system

欠驱动半挂汽车列车的运动建模与跟踪控制

You Feng , Zhang Rong-hui , Wang Hai-wei

游峰, 张荣辉, 王海玮

摘　要：应用车辆系统动力学理论,建立了以车辆参考坐标系和地面坐标系的欠驱动汽车列车动态模型。为了简化验算和求解过程,采用准确线性化方法对建立的系统模型进行线性化。在此基础上,针对小曲率转弯半径的车辆运行轨迹,建立了极坐标下的汽车挂车系统运动学模型,应用滑模变结构控制理论,给出了车辆系统状态变量向超平面收敛的方法。最后,对平滑运动轨迹和小曲率转弯半径的跟踪控制进行了仿真分析。仿真实验结果表明：所设计的反馈控制器能改善汽车列车对行驶路线的跟踪能力,使偏离的车辆快速返回到期望的稳态轨迹上。

... 游峰等^[10]建立了欠驱动汽车列车动力学模型,应用滑模变结构理论给出了车辆系统状态变量向超平面收敛的方法,对平滑运动轨迹和小曲率转弯半径的轨迹有良好的跟踪能力 ...

2014

0.0

. 2014, 33(6):161-166 DOI:doi:10.3969/j.issn.1674-0696.2014.06.34

Out value algorithm of tractor semitrailer combinations

一种半挂汽车列车外摆值的计算方法

Duan Bin , Shan Ying-chun , Liu Xian-dong

段斌, 单颖春, 刘献栋

根据GB 1589—2004和GB/T 12540—2009对外摆值的定义、限值和实验测试方法,参考半挂汽车列车在转弯通道圆内转弯过程的作图法,对半挂汽车列车外摆值的数值计算方法进行了研究。首先,研究了基于惯性坐标系和连体坐标系转弯过程的定量分析方法,推导出了半挂汽车列车外摆值的计算方法,并针对具体的车辆进行了数值计算与分析。然后,计算分析了牵引车与半挂车几何参数变化对外摆值的影响规律。最后,为验证所提半挂汽车列车外摆值数值计算方法的正确性,利用Truck Sim工程软件进行了半挂汽车列车外摆值仿真,同时还进行了实车试验。研究结果表明:该算法计算结果准确、公式简洁、便于理解和工程实用,可为半挂汽车列车的通过性研究提供指导。

... 段斌等^[11]根据国标中对外摆值的定义、限值和实验测试方法,对外摆值的数值计算方法进行了研究,利用TruckSim仿真和实车试验对此算法进行了验证,为半挂汽车列车的通过性研究提供了一种思路 ...

0.0

. , 2015(10):9-10 DOI:doi:10.15913/j.cnki.kjycx.2015.10.009

ADAMS and MATLAB based active steering car train simulation study

基于ADAMS和MATLAB主动转向式汽车列车转向仿真研究

Liu Zhao-tao , Wang Yong-wei , Tan Ya-hong.

刘朝涛, 王永伟, 谭亚红

为了降低汽车列车转弯半径和行驶轨迹良好的跟随性,可增加挂车的数量.基于汽车列弯路转向理论,运用ADAMS建立了列车运动学、动力学模型,运用MATLABL建立了列车转向控制模型,进行了ADAMS与MATLAB的联合仿真,并对主动转向汽车列车的可行性、优越性进行了验证.

... 刘朝涛^[12]通过ADAMS建立了具有两节全挂车的汽车列车的运动学和动力学模型,建立了列车的转向控制MATLAB模型,通过联合仿真对主动转向汽车列车的可行性、优越性进行了验证 ...

0.0

. , 2016(2):79-82

Simulation analysis of the steering characteristics of semi-dragging trucks based on TruckSim