步行交通规划交叉路口行人瞬时动态拥塞疏散模型

引用本文

苏书杰, 何露. 步行交通规划交叉路口行人瞬时动态拥塞疏散模型. 2018, 48(2): 440-447
SU Shu-jie, HE Lu. Transient dynamic congestion evacuation model of pedestrian at walk traffic planning crossroads. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 440-447 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170037
Permissions

步行交通规划交叉路口行人瞬时动态拥塞疏散模型

苏书杰¹, 何露²

1.长安大学公路学院,西安 710061

2.中船重工第722研究所,武汉 430079

作者简介:苏书杰(1983-),女,工程师,博士研究生.研究方向:交通运输规划与管理. E-mail:sushujie788@163.com

基金项目:国家自然科学基金青年科学基金项目(61402365)

摘要

针对瞬时动态拥塞中交叉路口行人拥挤中存在较强相互力学作用,常规疏散方法缺少符合相互接触摩擦的力学多变瞬时动态特征的约束参数,几乎都以人群无接触为假设条件,导致疏散过程效率、稳定性和分布均衡度较差的问题,构建了基于元胞自动机的行人瞬时动态拥塞疏散模型,对其进行解决。在模型构建中对瞬时动态拥塞的力学约束参数进行获取,在力学参数约束下,将疏散时间较长路径的流量转移至最短路径上,利用元胞自动机求解疏散瞬时动态用户最优状态。仿真测试实验表明,该模型在多疏散口及单一疏散口进行分析时,交叉路口的行人拥挤疏散效率、行人服从疏散率和疏散分布均衡度均有提高,具有一定的优势。

关键词: 交通运输系统工程; 交叉路口; 元胞自动机; 行人拥挤; 瞬时动态

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2018)02-0440-08

Transient dynamic congestion evacuation model of pedestrian at walk traffic planning crossroads

SU Shu-jie¹, HE Lu²

1.College of Highway,Chang'an University, Xi'an 710061, China

2.722th Research Institute of CSIC,Wuhan 430079,China

Abstract

In transient dynamic congestion, there is a strong interaction among the intersection pedestrian. The conventional mechanical evacuation method lacks friction constraint parameters with changeable instantaneous dynamic characteristics, and assumes that there is no contact among the pedestrian. This results in poor evacuation process efficiency, poor stability and poor distribution equilibrium degree. To solve the above problem, a pedestrian transient dynamic congestion evacuation model based on cellular automata is proposed. First, the mechanical constraint parameters of the transient dynamic congestion are obtained. Then, under the constraint of these mechanical parameters, the traffic flow of the longer evacuation path is transferred to the shortest path. Finally, the cellular automata is used solve the transient dynamic optimal state of the user. Simulation results show that, applying the proposed model to multiple evacuation ports and single evacuation ports, the pedestrian congestion evacuation efficiency, pedestrian compliance rate and the equilibrium degree of evacuation distribution are improved.

Key words: engineering of communications and transportation system; intersection; cellular automata; pedestrian congestion; transient dynamics

Show Figures

0 引言

近年来, 随着城市人员的大量增加, 在交叉路口处多种灾害和突发事件所引发的行人过度拥挤以及踩踏等事故屡见不鲜^[1], 由此对交叉路口行人进行疏散显得尤为重要^{[2, 3]}。鉴于步行交通规划中交叉路口行人拥挤疏散的重要性, 张磊等^[4]以安全出口前的行人流作为研究对象, 分析拥挤致伤生成机理, 基于行人的位置与安全出口之间的距离, 进而生成趋向安全出口方向拥挤力; 加入了拥挤力的效果以及合力参数, 并分别描述了外界拥挤力对行人作用效果以及作用合力; 加入吸收系数以及抗死伤系数, 描述拥挤力在传递时行人对外界的拥挤力吸收和抵抗能力。实验表明, 随着吸收系数或者抗死伤系数的不断增加, 该方法能够有效预防疏散行人的拥挤致伤, 不过存在疏散效率低的问题。针对多出口条件下行人自主疏散时盲目选择疏散出口而导致出口的利用不对称等问题, 李明华等^[5]对行人由单个拥挤出口的疏散时间进行了计算, 并据此构成了该模型混合遗传模拟退火求解算法, 提出了出口的选择确定仿真模型。该方法存在疏散效率低的问题。胥旋等^[6]提出了大规模人群分区疏散优化法, 该方法将疏散时间最短作为目标, 并综合考虑人群分布以及出口位置等因素, 依据迭代计算, 求解每个行人最优出口的选择, 得到优化疏散分区结果。实验表明, 采用优化分区疏散时部分人员放弃路最短径出口, 而选取了较宽且附近人员的密度较低的出口, 提高了整体疏散效率, 但是疏散稳定性较差。为此, 本文提出一种基于元胞自动机的步行交通规划中交叉路口行人拥挤疏散方法。

1 瞬时交叉路口行人拥挤疏散建模

随着城市化的不断发展, 为了满足大量密集人口的社会需求, 步行交通规划中的交叉路口行人拥挤疏散方法应运而生^{[7, 8]}。本文利用元胞自动机对步行交通规划中交叉路口行人拥挤进行疏散。

1.1 瞬时动态拥挤中的力学模式约束参数

基于计划行为原理, 构建两大交叉路口行人疏散的模式, 分析行人疏散对交通性能的影响因素, 组建完整的疏散模式。

在磁力模式中, 将行人、障碍物定义成正极, 把目的地定义成负极, 利用同性相斥、异性相吸的磁力学定律^{[9, 10, 11]}, 行人与目的地间的吸引力用F表示, k为常数, q₁为行人所处位置磁场强度, q₂为目的磁极强度, r为行人到目的地之间的距离。

$\vec{F}$ = $\begin{matrix} \frac{k \cdot q_{1} \cdot q_{2}}{r^{3}} \end{matrix}$ (1)

行人与其他行人以及障碍物间的排斥力约束为:

a=v· cosα · tanβ (2)

式中:v为行人的速度; α 为该行人与其他行人之间所呈排斥力的角度; β 为该行人与障碍物之间所呈排斥力的角度。

利用社会力模式对疏散行人走路的过程进行分析, 其中主要包括3种力:①基于社会心理— 目标驱动力; ②人与人— 作用力; ③人与障碍物— 作用力。

m_i $\begin{matrix} \frac{d v_{i}}{dt} \end{matrix}$ =m_i $\begin{matrix} \frac{v_{i}^{0} e_{i}^{0} - v_{i}}{τ_{i}} \end{matrix}$ + $\begin{matrix} \sum_{j (j \neq i)} \end{matrix}$ f_ij+f_iw(3)

式中: $\begin{matrix} \sum_{j (j \neq i)} \end{matrix}$ f_ij为i受到其他人相互作用力的合力; f_ij为j相对i的相互作用力合力, 其中包含法向分量f_ijn、切向分量f_ijτ。

f_ij=f_ijnn_ij+f_ijττ _ij(4)

f_ijn=A_iexp $\begin{matrix} [\frac{r_{ij} - d_{ij}}{B_{i}}] \end{matrix}$ n_ij+kθ $\begin{matrix} (r_{ij} - d_{ij}) \end{matrix}$ n_ij(5)

f_ijτ=kθ $\begin{matrix} (r_{ij} - d_{ij}) \end{matrix}$ Δ τ _ij(6)

式中:k为人与人之间作用力的综合系数; θ 为人与人之间作用力的效果系数; r_ij为两人尺寸半径之和; d_ij(t)=‖ x_i(t)-x_j(t)‖ 为两人于t时刻生成的距离; A_iexp $\begin{matrix} [(r_{ij} - d_{ij}) / B_{i}] \end{matrix}$ n_ij为因社会心理生成的人与人之间为了保持距离生成的作用力, 斥力大小、人与人间距离的相关性^{[12, 13]}, 采用一个指数函数来表达, 在已确定的距离内, 斥力大小会达到最大值, 且会随着距离的不断增大而减小, 直至为零, 该表征项诠释了普通的行人在行走时方向与速度之间的变化。

在下面的研究中, f_iω为i受到障碍物、行动边界影响的合力, f_iω为法向、切向两个分力的约束形式。具体如下式所示:

f_iω=f_{iω n}n_ij+f_{iω τ}τ _ij(7)

f_{iω n}=A_iexp $\begin{matrix} [\frac{r_{iω} - d_{iω}}{B_{i}}] \end{matrix}$ n_iω+kθ $\begin{matrix} (r_{iω} - d_{iω}) \end{matrix}$ n_iω(8)

f_{iω τ}=kθ $\begin{matrix} (r_{iω} - d_{iω}) \end{matrix}$ Δ τ _iω(9)

社会力模式其实是描述了疏散行人行为、行人心理因素间存在的联系, 其量化性地表述了疏散行人期望速度所生成的驱动力、周边事物对疏散行人吸引力等^[14^-^16]。利用疏散行人间、行人与环境间的相互作用, 进而研究疏散行人的心理和行为间存在的关联, 并强调疏散行人活动具有随机性, 反映了人本身的某些行为、心理特征。社会模型内的各项参数都具有实际的物理意义, 且仿真微观行为的拟真度比较高, 硬件运算能力要求也比较高, 且随着计算机技术的逐渐升级, 针对模拟疏散环境下的人员典型逃生行为方法也较为真实有效。

1.2 交叉路口行人拥挤疏散瞬时动态用户最优状态求解

根据以上对瞬时动态拥挤中的力学模式约束参数确定结果, 需将疏散过程中的每个人均希望选择最短路径尽快疏散出去^{[17, 18, 19]}。如果行人根据当前各路径的瞬时行走时间作为自身距离选择依据, 假设每个人都选取目前的疏散时间作为最短路径, 且无人能够改变路径^[20]来减少本身的瞬时行走时间, 达到瞬时动态用户最优的状态。这时所有可利用的疏散路径都有相同的瞬时疏散时间阻抗, 该阻抗等于最小疏散时间。对于所有的未被使用的疏散路径, 瞬时疏散时间均不会小于最小瞬时疏散时间, 即所求得瞬时动态用户最优状态。假设第k个时段元胞I中有行人选择路径p从出口元胞D疏散( $\begin{matrix} f_{p}^{I, D} \end{matrix}$ (k)> 0), 则该路径的瞬时疏散时间最小。假设无人于第k个时段选取疏散路径p( $\begin{matrix} f_{p}^{I, D} \end{matrix}$ (k)=0), 则该路径的瞬时疏散时间, 绝对不会少于最小疏散时间。基于疏散路径瞬时动态用户状态数学表达式为:

$\begin{matrix} \{\begin{matrix} c_{p}^{I, D} (k) = π (k), f_{p}^{I, D} (k) > 0 \\ c_{p}^{I, D} (k) = π_{p} (k), f_{p}^{I, D} (k) \leq 0 \end{matrix} \end{matrix}$ (10)

上述最优路径选择条件可转变为非线性互补问题:

$\begin{matrix} \{\begin{matrix} f_{p}^{I, D} (k) [c_{p}^{I, D} (k) - π_{p} (k)] = 0 \\ \sum_{D} \sum_{p} f_{p}^{I, D} (k) = n_{I} (k) \\ c_{p}^{I, D} (k) - π_{p} (k) \geq 0 \\ f_{p}^{I, D} (k) \geq 0 \end{matrix} \end{matrix}$ (11)

上述问题模型是基于路径的动态路径选择问题, 求解过程要将路径的瞬时动态用户最优状态模型转换为基于路段的瞬时动态用户最优状态模型。其核心思想为:如果元胞I上行人选取某最短路径p走到出口D时, 就必须通过其相邻元胞J, 如果路径p是最小的时间阻抗路径时, 则必有 $\begin{matrix} f_{p}^{I, D} \end{matrix}$ (k)> 0, 也就是说, 第k时段在元胞I中经过由元胞J于出口D所疏散的行人大于零, 也就是 $\begin{matrix} n_{j}^{I, D} \end{matrix}$ (k)'> 0。相反的如果路径p不是最小的时间阻抗路径, $\begin{matrix} f_{j}^{I, D} \end{matrix}$ (k)=0, 就是说第k时段在元胞I中经由元胞J于出口D所疏散的行人为零, 也就是 $\begin{matrix} n_{J}^{I, D} \end{matrix}$ (k)=0。据此可知, 基于元胞路段的疏散行人瞬时动态用户最优状态可表示为:

$\begin{matrix} \{\begin{matrix} c_{J}^{I, D} (k) = π_{I} (k), n_{J}^{I, D} (k) > 0 \\ c_{J}^{I, D} (k) = π_{D} (k), n_{J}^{I, D} (k) \leq 0 \end{matrix} \end{matrix}$ (12)

在疏散行人时, 疏散出口等瓶颈处的通行能力下降致使形成排队等待, 排队时间是行人疏散时间的重要组成部分。则第k个时段元胞I中的行人经由元胞J∈ R_I移动至出口D队列队尾的行走时间可以按照下式计算:

$\begin{matrix} T_{j}^{I, D} \end{matrix}$ (k)=T_IJ(k)+(k) (13)

由此, 在k时段进行疏散路径的选取时, 需要对时段l内各出口排队人数进行估算。根据上述计算, 如果行人在 $\begin{matrix} T_{j}^{I, D} \end{matrix}$ (k)时间之内至出口元胞D, 即满足l≤ $\begin{matrix} T_{j}^{I, D} \end{matrix}$ (k)< l+1, 否则 $\begin{matrix} ξ_{J, k}^{I, D} \end{matrix}$ =0。在这里采用点排队模型对出口位置的排队行人数估算。对时段k进行考虑, 行人估计于时段l到出口D, 这个时候的出口D的排队长度可根据下式进行计算:

$Q_{k}^{D} (l) = \begin{matrix} \{\begin{matrix} \max \{Q_{k}^{D} (l - 1) + ξ_{J, k}^{I, D} (l) - δ_{S^{D}} (k), 0\}, l \geq k \\ 0, 其他 \end{matrix} \end{matrix}$ (14)

式中:S^D(k)为关于出口宽度的函数。

整体交叉路口行人拥挤疏散时间是由行走时间及排队时间所组成, 所以第k个时段的元胞I中行人经相邻元胞J∈ R_I并从出口D疏散的时间计算公式为:

$\begin{matrix} ξ_{J, k}^{I, D} \end{matrix}$ = $\begin{matrix} T_{J}^{I, D} \end{matrix}$ + $\begin{matrix} \frac{Q_{k}^{D} [k + T_{J}^{I, D} (l)]}{δ_{S^{D}} (l)} \end{matrix}$ (15)

综合上述, 在这里利用启发式迭代法对交叉路口行人拥挤瞬时动态用户最优状态求解, 具体过程如下:

(1)设置循环变量η =1, 在Ω 中选取各元胞的初始流量 $\begin{matrix} n_{J}^{I, D} \end{matrix}$ (k), 且每个元胞I∈ R, 通过每个行人的所处位置来统计元胞I内行人数量和密度。对每个元胞J∈ R_I, 依据下式对元胞I和J之间的行走时间Γ _IJ(k)和T_IJ(k)进行计算:

Γ _IM(k)=max $\begin{matrix} \{Γ_{IM}^{0}, Γ'_{IM} (k), \frac{N_{IM} (k)}{S_{IM} (k)}\} \end{matrix}$ (16)

T_IM(k)=max $\begin{matrix} \{T'_{IM} (k), \frac{N_{IM} (k)}{N_{I} (k)}, \frac{N_{IM} (k)}{S_{IM} (k)}\} \end{matrix}$ (17)

(2)对于每个元胞I∈ R, 根据式(13)计算移动时间 $\begin{matrix} T_{J}^{I, D} \end{matrix}$ (k), 并依次确定 $\begin{matrix} ξ_{J, k}^{I, D} \end{matrix}$ , 根据式(14)和式(15)计算排队长度和最终预估的疏散时间 $\begin{matrix} c_{J}^{I, D} \end{matrix}$ (k)。利用下式计算最小的疏散时间π _I(k), 以及对应的元胞集合 $\begin{matrix} {\overset{⌒}{R}}_{I} \end{matrix}$ :

$\begin{matrix} \{\begin{matrix} π_{I} (k) = \min_{J \in R_{I}} \{c_{J}^{I, D} (k)\} \\ {\overset{⌒}{R}}_{I} = \{(J, D) |c_{J}^{I, D} (k) = π_{I} (k)\} \end{matrix} \end{matrix}$ (18)

(3)对于元胞集合J∈ $\begin{matrix} {\overset{⌒}{R}}_{I} \end{matrix}$ , 更新元胞流量, 得到判断动态用户收敛条件为:

$\begin{matrix} n_{J}^{I, D} \end{matrix}$ (k)= $\begin{matrix} \{\begin{matrix} n_{J}^{I, D} (k) - α n_{J}^{I, D} (k), (J, D) \notin R_{I} \\ n_{J}^{I, D} (k) + ν / |{\overset{}{R}}_{I}|, (J, D) \in R_{I} \end{matrix} \end{matrix}$ (19)

式中:α 和ν 分别为动态用户的移动系数和平均移动速度。

(4)经式(19)判断收敛条件, 假设满足判断收敛条件, 则停止迭代, 得到动态用户最优解, 否则令η =η +1, 返回到步骤(2), 依据每个行人的位置统计元胞I内行人数量和密度, 动态用户最优解为:

ε = $\begin{matrix} \frac{\sum_{I \in R} \sum_{J \in R_{I}} \sum_{D} n_{J}^{I, D} (k)}{\sum_{I \in R} \sum_{J \in R_{I}} \sum_{D} n_{J}^{I, D} (k) π_{I} (k)} \end{matrix}$ (20)

(5)完成交叉路口行人拥挤瞬时动态用户最优状态求解。

2 实验结果与分析

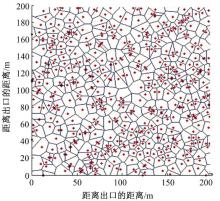
根据交叉路口环境以及主题特点和行人疏散特征的不同, 本文选取了一个较为普通的交叉路口作为实验环境, 实验平台搭建在Visual C上, 具体为一个200 m× 200 m的交叉路口, 大体有4个方向, 依据障碍物与出口位置, 把该场景分为120个元胞, 元胞长度为1~3 m不等, 通过相邻元胞数量, 把120个元胞划分两个集合, 则其实验仿真环境如图1所示, 图中菱形块表示一个元胞, 即一人。在上述的实验参数和实验环境下, 分别对多个出口及单一出口情况的疏散画面进行仿真分析。

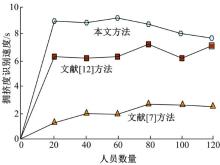
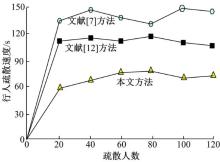
	Figure Option View Download New Window
	图1 实验仿真环境图Fig.1 Experimental simulation environment diagram

当出口为多个且发生瞬时拥堵时, 采用不同方法与本文所提方法进行对比验证, 如图2、图3所示。

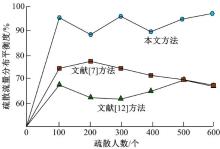
	Figure Option View Download New Window
	图2 不同方法每条疏散路径的拥挤程度对比Fig. 2 Comparison of congestion degree of each evacuation path in different methods

	Figure Option View Download New Window
	图3 不同方法拥挤度识别速度对比Fig.3 Comparison of congestion identification speed in different methods

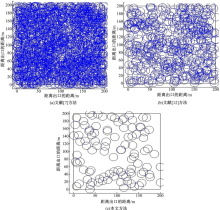
分析图2和图3可知, 在200 m× 200 m区域内, 采用文献[7]方法时拥堵程度较高, 人与人之间无多余的孔隙, 拥挤度识别速度不理想; 采用文献[10]方法较文献[7]方法拥堵程度有所降低, 但人与人之间还是存在一定的碰撞, 拥挤度识别速度较慢; 采用文献[12]方法时拥堵程度有所缓解, 识别速度有提高, 但相比本文方法, 其拥堵程度和拥挤度识别速度不是很显著; 采用本文方法的拥挤识别速度最快, 每条疏散路径的拥挤程度最低, 而且可清晰地看出人员分布情况。由于本文对交叉路口行人瞬时动态拥挤中的力学模式约束参数进行了力学分析, 因而提高了整体拥挤度识别速度, 同时也减少了每条疏散路径的拥挤程度。

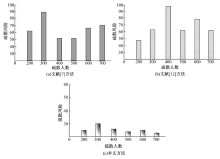
当出口为单一且产生瞬时拥堵时, 在行人疏散仿真分析时需要考虑单一出口对疏散结果造成的干扰及疏散速度的变化, 如图4和图5所示。

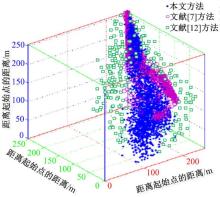	Figure Option View Download New Window
	图4 不同疏散方法在单一出口时疏散效果对比Fig.4 Comparison of evacuation effects of different evacuation methods at a single outlet

	Figure Option View Download New Window
	图5 不同方法疏散速度对比Fig.5 Comparison of evacuation speed of different methods

根据图4和图5的对比结果可观察到, 采用文献文献[7]方法时, 所需疏散人员大量聚集在出口处, 且距离出口处越近的地方人员越密集, 疏散效果越差, 导致在瞬时拥堵时, 人员疏散速度达到138 s; 采用文献[12]方法时, 虽然在出口处, 人员较为稀松, 但整体面积较大, 人员疏散速度达到114 s; 采用本文方法时, 疏散人员排列紧密, 越接近出口, 人员越少, 降低了在出口处拥挤, 导致疏散速度慢的问题, 且本文方法疏散速度最快的约为83.4 s, 主要是由于本文方法运算能力要求也比较高, 且随着计算机技术的逐渐升级, 针对模拟疏散环境下的人员逃生行为较为真实有效, 由此提高了本文方法的疏散速度。

将文献[7]、文献[12]方法和本文方法均迭代3次, 观察不同方法的疏散风险变化趋势, 实验结果如图6所示。图7为不同方法进行疏散行人对疏散指向的信任度对比。图8为不同方法疏散的行人对疏散方案的服从率对比。

分析图6、图7和图8可知, 在疏散风险、疏散行人对疏散指向的信任度以及行人对疏散方案的服从率方面, 本文方法明显优于文献[7]和文献[12]方法。首先, 在疏散风险方面进行3次迭代, 本文方法疏散时存在的风险依然比较小, 总体效果良好; 其次, 在行人对疏散指向的信任度方面, 本文方法的取信度一直很高, 且信任度曲线较为平缓; 最后, 在行人对疏散方案的服从率方面, 行人对本文方法的服从率大致集中在98%以上。以上结果均证明了本文方法具有绝对的优越性和可靠性。

	Figure Option View Download New Window
	图6 不同方法的疏散风险Fig.6 Evacuation risk of different methods

	Figure Option View Download New Window
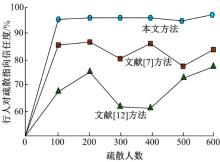	图7 不同方法疏散行人对疏散指向信任度对比Fig.7 Comparison of evacuation points’ trust degree in different methods of evacuation

	Figure Option View Download New Window
	图8 不同方法行人对疏散方案的服从率对比Fig.8 Comparison of pedestrians’ compliance rate of evacuation schemes in different ways

为了进一步验证本文方法的有效性, 采用Matlab仿真软件进一步进行验证, 不同方法疏散分布均衡度对比仿真结果如图9和图10所示。

由图9和图10可知, 采用文献[7]方法时, 多处存在变形及变细的现象, 降低了人群疏散分布均衡度, 约为70.2%; 采用文献[12]方法时, 从一开始到出口, 一直呈现出凹型, 即出现大面积拥挤, 导致平均人群疏散分布均衡度降低, 约为62.3%; 采用本文方法时, 只有在出口处呈现出变细的现象, 这是由于出口大小导致的, 但其余时间未出现拥堵, 人群疏散时的分布均衡度达到了90.8%, 具有一定的优势。

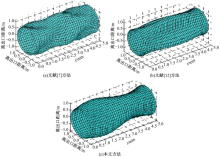	Figure Option View Download New Window
	图9 不同方法疏散分布均衡度对比仿真图Fig.9 Contrast simulation of equilibrium degree of evacuation distribution in different methods

	Figure Option View Download New Window
	图10 不同方法疏散人流分布均衡度对比Fig.10 Comparison of distribution equilibrium degree of evacuation in different methods

3 结束语

本文在对步行交通规划中交叉路口行人拥挤进行疏散时, 分别对疏散模式和疏散求解进行了分析, 实验表明, 本文方法对多疏散口及单一疏散口进行分析时, 交叉路口的行人拥挤疏散效率、行人服从疏散率和疏散分布均衡度均有提高, 具有很高的可行性和稳定性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zhang Yao. Study on optimization of uban traffic congestion evacuation route[J]. Computer Simulation, 2017, 34(2): 200-203. [本文引用:1]
[2]	Takayanagi H, Yamada S, Shibahara H, et al. A study on evaluation method for local congestion in pedestrian space by using of traj-scalar model[J]. Aij Journal of Technology & Design, 2016, 22(52): 1067-1071. [本文引用:1]
[3]	Cao S, Song W, Lv W. Modeling pedestrian evacuation with guiders based on a multi-grid model[J]. Physics Letters A, 2016, 380(4): 540-547. [本文引用:1]
[4]	张磊, 岳昊, 李梅, 等. 拥堵疏散的行人拥挤力仿真研究[J]. 物理学报, 2015, 64(6): 060505. Zhang Lei, Yue Hao, Li Mei, et al. Simulation of pedestrian push-force in evacuation with congestion[J]. Acta Physica Sinica, 2015, 64(6): 060505. [本文引用:1]
[5]	李明华, 袁振洲, 许琰, 等. 基于点排队模型的多出口疏散优化模型研究[J]. 交通运输系统工程与信息, 2015, 15(4): 166-172. Li Ming-hua, Yuan Zhen-zhou, Xu Yan, et al. An optimization model of multi-exit evacuation based on point queue model[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(4): 166-172. [本文引用:1]
[6]	胥旋, 史聪灵, 伍彬彬, 等. 人群分区疏散优化算法研究[J]. 中国安全生产科学技术, 2016, 12(11): 153-158. Xu Xuan, Shi Cong-ling, Wu Bin-bin, et al. Study on the optimization algorithm of the crowd partition evacuation[J]. Journal of Safety Science and Technology, 2016, 12(11): 153-158. [本文引用:1]
[7]	周继彪, 陈红, 闫彬, 等. 基于云模型的地铁换乘枢纽拥挤度辨识方法[J]. 吉林大学学报: 工学版, 2016, 46(1): 100-107. Zhou Ji-biao, Chen Hong, Yan Bin, et al. Identification of pedestrian crowding degree in metro transfer hub based on normal cloud model[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(1): 100-107. [本文引用:1]
[8]	Djehiche B, Siwe A T, Tembine H. A mean-field game of evacuation in multi-level building[J]. IEEE Transactions on Automatic Control, 2017, 8(99): 1-22. [本文引用:1]
[9]	Tan L, Wu L, Lin H. An individual cognitive evacuationbehaviour model for agent-based simulation: a case study of a large outdoor event[J]. International Journal of Geographical Information Science, 2015, 29(9): 1552-1568. [本文引用:1]
[10]	Zhang L, Yue H, Li M, et al. Simulation of pedestrian push-force in evacuation with congestion[J]. Acta Physica Sinica, 2015, 64(6): 10-15. [本文引用:1]
[11]	Zhou M, Dong H, Wen D, et al. Modeling of crowd evacuation with assailants via a fuzzy logic approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(9): 2395-2407. [本文引用:1]
[12]	Solmaz G, Turgut D. Pedestrian mobility in theme park disasters[J]. IEEE Communications Magazine, 2015, 53(7): 172-177. [本文引用:1]
[13]	Carrillo J A, Martin S, Wolfram M T. An improved version of the Hughes model for pedestrian flow[J]. Mathematical Models & Methods in Applied Sciences, 2016, 26(4): 671-697. [本文引用:1]
[14]	You L, Hu J, Gu M, et al. The simulation and analysis of small group effect in crowd evacuation[J]. Physics Letters A, 2016, 380(41): 3340-3348. [本文引用:1]
[15]	Jiang X. Simulationmodel of pedestrian evacuation in high-rise building: considering group behaviors and real-time fire[J]. International Journal of Smart Home, 2015, 9(2): 81-92. [本文引用:1]
[16]	Wang J, Jin Z, Hilton R G, et al. Controls on fluvial evacuation of sediment from earthquake-triggered land slides[J]. Geology, 2015, 43(2): 115-118. [本文引用:1]
[17]	Karbovskii V, Voloshin D, Karsakov A, et al. Multiscale agent-based simulation in large city areas: emergency evacuation use case[J]. Procedia Computer Science, 2015, 51(1): 2367-2376. [本文引用:1]
[18]	Tsiftsis A, Georgoudas I G, Sirakoulis G C. Real data evaluation of a crowd supervising system for stadium evacuation and its hardware implementation[J]. IEEE Systems Journal, 2016, 10(2): 649-660. [本文引用:1]
[19]	Ronchi E, Nilsson D, Koji S, et al. A virtual reality experiment on flashing lights at emergency exit portals for road tunnel evacuation[J]. Fire Technology, 2016, 52(3): 623-647. [本文引用:1]
[20]	Ronchi E, Kinateder M, Müller M, et al. Evacuation travel paths in virtual reality experiments for tunnel safety analysis[J]. Fire Safety Journal, 2015, 71(24): 257-267. [本文引用:1]

2017

0.0

... 0 引言近年来,随着城市人员的大量增加,在交叉路口处多种灾害和突发事件所引发的行人过度拥挤以及踩踏等事故屡见不鲜^[1],由此对交叉路口行人进行疏散显得尤为重要^[2,3] ...

2016

0.0

2016

0.0

2015

0.0

. 2015, 64(6):060505-

Simulation of pedestrian push-force in evacuation with congestion

拥堵疏散的行人拥挤力仿真研究

Zhang Lei , Yue Hao , Li Mei

张磊, 岳昊, 李梅

... 鉴于步行交通规划中交叉路口行人拥挤疏散的重要性,张磊等^[4]以安全出口前的行人流作为研究对象,分析拥挤致伤生成机理,基于行人的位置与安全出口之间的距离,进而生成趋向安全出口方向拥挤力 ...

2015

0.0

. 2015, 15(4):166-172

An optimization model of multi-exit evacuation based on point queue model

基于点排队模型的多出口疏散优化模型研究

Li Ming-hua , Yuan Zhen-zhou , Xu Yan

李明华, 袁振洲, 许琰

摘　要：针对室内多出口条件下,行人自主疏散时盲目选择疏散出口而导致的出口利用不对称问题,本文基于点排队模型计算了行人从单个拥挤出口疏散所耗时间,并据此构建了室内多出口条件下行人疏散的出口选择优化模型,设计了该模型的混合遗传模拟退火求解算法.同时,进一步提出了出口选择确定的元胞自动机仿真模型,用于仿真评估包括本模型优化解在内的多个出口选择方案对疏散时间的改善效果.结果表明,本文所提出的模型和方法,能够保证各个疏散出口的利用率均衡,降低总体疏散时间,对制定可行的疏散计划有一定参考意义.

... 针对多出口条件下行人自主疏散时盲目选择疏散出口而导致出口的利用不对称等问题,李明华等^[5]对行人由单个拥挤出口的疏散时间进行了计算,并据此构成了该模型混合遗传模拟退火求解算法,提出了出口的选择确定仿真模型 ...

2016

0.0

. 2016, 12(11):153-158 DOI:doi:10.11731/j.issn.1673-193x.2016.11.026

Study on the optimization algorithm of the crowd partition evacuation

人群分区疏散优化算法研究

Xu Xuan , Shi Cong-ling , Wu Bin-bin

胥旋, 史聪灵, 伍彬彬

摘　要：在疏散过程中,出口利用不均现象时有发生,距离最短路径并不一定是最快的路径。提出了大规模人群分区疏散优化算法,该算法以疏散时间最短为目标,综合考虑了人群分布、出口位置、出口宽度等因素,通过迭代计算,求解每个行人的最优出口选择,从而得到优化疏散分区结果。以具有多个出口的某大型步行商业街区疏散为例,利用经典的无后退有偏随机行走模型进行模拟计算,对是否采用优化分区的疏散时间进行了比较分析。结果表明：采用优化分区疏散时,部分人员放弃路径最短的疏散出口,而被导向选择宽度较宽和附近人员密度较低的出口,从而提高整体疏散效率。该算法解决了以距离最短为目标的疏散分区方式导致的出口利用不均和不充分的现象,有效提高了疏散效率,对于区域分区疏散策略的制定具有一定指导意义。

... 胥旋等^[6]提出了大规模人群分区疏散优化法,该方法将疏散时间最短作为目标,并综合考虑人群分布以及出口位置等因素,依据迭代计算,求解每个行人最优出口的选择,得到优化疏散分区结果 ...

2016

0.0

. 2016, 46(1):100-107 DOI:doi:10.13229/j.cnki.jdxbgxb201601015

Identification of pedestrian crowding degree in metro transfer hub based on normal cloud model

基于云模型的地铁换乘枢纽拥挤度辨识方法

Zhou Ji-biao , Chen Hong , Yan Bin

周继彪, 陈红, 闫彬

In order to solve the problems of fuzziness and randomness in the division of congestion state in metro transfer hub, an identification method of pedestrian crowding degree factor is proposed based on normal cloud model. First, the connotation and the measure standard of the pedestrian crowding degree are analyzed, and according to their boundary value under different service level the digital characteristics of the cloud are calculated. Second, the cloud synthesis theory is applied to establish the template cloud corresponding to different service levels, and the survey data (pedestrian speed, flow etc.) are input into the cloud generator in order to set up the identification cloud model. Third, according the definition of cloud similarity, the similarity between the identified cloud and the template cloud in the infrastructure (e.g. channel, stairs) is calculated. Moreover, the crowding degree is defined independently, which is described in a quantificational level under the state of crowding degree in the metro transfer hub, and the method to identify the pedestrian crowding degree is given. The method is verified by a case study in a metro transfer hub in Xi'an. Results show that the pedestrian crowding degree in the channel 100.095, which is in the crowding state, the pedestrian crowding degree in the stair is 100.273, which is also in the crowded state. This method can not only accurately identify the crowded state quantificationally, but also reflect the change process of pedestrian crowding degree, which has strong practicality.

针对地铁换乘枢纽拥挤状态划分中的模糊性和随机性,提出了一种基于云模型的地铁换乘枢纽行人拥挤度辨识方法。首先分析行人拥挤度的内涵和度量标准,根据它们在不同服务水平下边界值计算云的数字特征。其次利用云的合成理论建立不同服务水平对应的模板云模型,同时将采集到的行人交通特性基本参数输入到枢纽内各基础设施的云发生器中,建立待识别云模型。然后根据云相似度计算模板云和待识别云的相似度并引入拥挤度定义,给出拥挤度辨识的具体实现过程。最后以西安市北大街地铁换乘枢纽为例对其进行了试验验证。结果表明:通过实际采集的数据建立待识别云模型,并与模板云作相似度分析,得出通道该时刻的行人拥挤度为100.095,处于拥挤状态;楼梯该时刻的行人拥挤度为100.273,处于拥挤状态。该方法不仅能够较准确地定量辨别枢纽内行人拥挤度状态,而且能够反映行人拥挤的程度和拥挤的变化过程,有较强的实用性。

... 1 瞬时交叉路口行人拥挤疏散建模随着城市化的不断发展,为了满足大量密集人口的社会需求,步行交通规划中的交叉路口行人拥挤疏散方法应运而生^[7,8] ...

2017

0.0

2015

0.0

... 在磁力模式中,将行人、障碍物定义成正极,把目的地定义成负极,利用同性相斥、异性相吸的磁力学定律^[9,10,11],行人与目的地间的吸引力用F表示,k为常数,q₁为行人所处位置磁场强度,q₂为目的磁极强度,r为行人到目的地之间的距离 ...

2015

0.0

2016

0.0

2015

0.0

... A_iexp (rij-dij)/Bin_ij为因社会心理生成的人与人之间为了保持距离生成的作用力,斥力大小、人与人间距离的相关性^[12,13],采用一个指数函数来表达,在已确定的距离内,斥力大小会达到最大值,且会随着距离的不断增大而减小,直至为零,该表征项诠释了普通的行人在行走时方向与速度之间的变化 ...

2016

0.0

2016

0.0

2015

0.0

2015

0.0

... 社会力模式其实是描述了疏散行人行为、行人心理因素间存在的联系,其量化性地表述了疏散行人期望速度所生成的驱动力、周边事物对疏散行人吸引力等^[14^-^16] ...

2015

0.0

... 2 交叉路口行人拥挤疏散瞬时动态用户最优状态求解根据以上对瞬时动态拥挤中的力学模式约束参数确定结果,需将疏散过程中的每个人均希望选择最短路径尽快疏散出去^[17,18,19] ...

2016

0.0

2016

0.0

2015

0.0

... 如果行人根据当前各路径的瞬时行走时间作为自身距离选择依据,假设每个人都选取目前的疏散时间作为最短路径,且无人能够改变路径^[20]来减少本身的瞬时行走时间,达到瞬时动态用户最优的状态 ...