作者简介:焦玉玲(1968-),女,副教授,博士. 研究方向:物流系统优化与设备自动化技术. E-mail:jyling777@163.com
针对产品的流水装配线组织设计和装配线平衡问题,提出有向网络新方法。在实验室现有直线型装配线上对产品(车模)进行产品结构分析,并对流水装配进行组织设计,获得了各工序时间和紧前关系,但产线平衡率不高。为提高生产效率,对产品的装配过程建立了数学模型。利用有向加权网络理论计算了模型中优先关系权重,实现了计算机程序计算,并用启发式算法对四驱车模型装配工序重新分配,设计双U型装配线。将U型装配线与现有直线型装配线进行了比较,平衡率提高了9.4%,验证了模型和算法的有效性和优越性,有向网络理论提高了运算效率,并为计算大型装配线平衡问题提供了新的方法。
A new method of directed weighted network is proposed to solve the problems of assembly line design and assembly line balancing. The structure of the product (car model) is analyzed on the existing linear assembly line in the laboratory, the assembly line is designed. The process time and preceded relationship between the tasks are obtained, and the line balance is not high. In order to improve the production efficiency, the mathematical model of the product assembly process is established. The weight of the priority relationship in the model is calculated using directed weighted network theory. The computer program is calculated and the assembly process of four wheel drive model is reconstructed by the heuristic algorithm. The U-shaped assembly line is compared with the existing linear assembly line, which shows that the balance rate is increased by 9.4%, thus verifying the superiority of the model and the algorithm. The weighted network theory improves the operation efficiency and provides a new method for calculation of the balance problem of large assembly line.
流水化装配线是进行大规模生产制造的高效生产方式。在社会需求逐渐变为多品种、小批量的客户定制化和产品多样化的情况下, 生产制造企业需要提高装配线机动性、柔性。装配线平衡问题(Assembly line balancing problem, ALB问题)[1]就是对整个生产装配线进行研究, 提高装配线平衡率。流水装配线组织设计是在满足节拍和作业之间先后顺序关系的前提下, 组合并分配作业, 使各工作站工时尽可能相等, 目的是减少装配线的闲置时间, 提高工人和设备的利用率。装配线平衡(ALB)问题的研究主要分为两种情况:一种是给定装配线节拍, 最小化装配线上的工作站数; 另一种是给定装配线的工作站数, 最小化装配线的节拍[2]。
1955年Salveson[3]提出了线性规划求解模型, 对于装配线平衡问题采用解析法来描述, 给出了求解装配线平衡问题最优解的求解过程。Jackson[4]在1956年提出求解装配线平衡问题的枚举法, 利用枚举法搜索在给定生产节拍的条件下工作站的最小数目, 以此获得最优解。Uur等[5]对于求解混合生产线平衡问题通过构造并行线路, 采用0-1整数规划模型, 算法主要通过引入新的参数来减少目标函数中的决策变量和约束条件中约束的数目。Miltenburg等[6]介绍了传统的直线型装配线和U型装配线并将两种装配线进行比较, 指出U型装配线的优点。Yegul等[7]介绍了一种混合的U型双边装配线, 并提出了多通道随机分配算法, 解决了小型的双边装配线平衡问题, 求出分配任务的顺序和装配线所需的最小工作站数目。Mura等[8]使用遗传算法解决多约束条件下装配线平衡过程中最小化工作站总数问题, 最后用案例说明了算法的可行性。Kucukkoc等[9]介绍了一种新型的平行U型装配线, 使用启发式算法求解最小工作站数, 但对于大型装配线平衡问题, 求解较为费时。本文引入有向网络法来解决大型计算的计算效率。
为了研究产品的流水装配线组织设计和装配线平衡问题, 在对四驱车车模进行产品结构、装配工艺流程分析的基础上, 在实验室流水装配线上模拟5个工作站分配装配工序测得流水作业节拍, 据此节拍建立数学模型, 应用有向网络图求解最小化U型装配线上的工作站数, 并设计了双U型装配线。
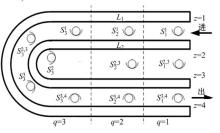
本文研究两条平行的U型装配线, 见图1, 用L1、L2分别表示两条U型装配线, 将U型装配线工作区域在平面上分成了4行(z=1, 2, 3, 4)和不同的列(q=1, 2, …, Q; Q为装配线队列的总数), 工作站用表示。企业可以根据产品结构和实际生产情况进行不同的工作站划分。两条相邻的装配线之间的工作站称为多线工作站(例如:, 等), 位于多线工作站的操作员可以在两条线上完成作业; 位于装配线内部(图中显示为L2)的工作站叫做交叉工作站(例如:
对于装配线平衡问题本文进行第一种情况研究, 即给定装配线节拍, 最小化装配线上的工作站数目。设定生产节拍用r表示, 作业元素集合用F={1, 2, …, k}表示, Fk表示第k个作业元素, 作业元素时间用T表示, 工作站用S表示, S={1, 2…, N}, Si表示第i个工作站所包含的作业元素集合。
在确定了生产节拍和作业元素时间之后, 装配线平衡就是在满足约束条件的前提下, 使工作站数目达到最小, 并使闲置时间最小, 装配线的平衡率达到最高。故装配线组织必须满足以下约束条件:
(1)同一个作业不能同时分配给两个工作站, 即不可能出现S1={1, 2, 3}, S2={1, 4, 5}。
(2)所有作业都必须分配到工作站, 即所有工作站作业元素集合的并集等于F。
(3)每个工作站内作业元素时间之和必须小于或等于生产节拍。
(4)所有作业元素必须按照作业元素优先关系图来分配到工作站。
建立装配线平衡问题数学模型如下。
目标函数:
minY={N× r-
约束条件:
Si
式中:N为工作站数目; r为生产节拍; k为第k个作业元素; T1(Fk)、T2(Fk)分别为分配给装配线L1 、L2的作业元素Fk的作业时间。
装配线中每个作业的分配都与作业元素紧前关系及后续作业数量有关。对于作业元素之间的优先关系, 根据有向图理论, 用优先关系矩阵来表示作业之间的紧前关系。故引入一个K维(K为作业元素个数)矩阵P(i, j), 表示各作业元素间的紧前关系, 其矩阵元素可定义如下:
P(i, j)=
根据优先关系图建立P矩阵, 根据作业时间表建立T列阵, P与T相乘求得T(Fk), 再求优先关系权重值, 步骤如下:
(1)计算每一个作业元素k的时间位置权重Ftk。
NTlk=T+
式中:Wk为作业元素k的后续作业元素集合; NTlk为作业元素k的作业时间与全部后续作业元素时间之和, l为第l条U型装配线, l=1或2; T为第k个作业元素的时间; T 为第k个作业元素的后续作业时间。
在装配线上, 根据NTlk值按升序排列所有的作业元素, 对于NTlk值最小的作业元素赋予时间位置权重Ftk=1, 对于NTlk值次小的作业元素赋予时间位置权重Ftk=2, 如果作业元素NTlk值相同, 则被赋予相同的时间位置权重Ftk。依次类推, 直到所有作业元素都被赋予Ftk。
(2)计算每一个作业元素k的后续作业量权重Fhk。
NHlk=Count{Wk}
式中:NHlk为作业元素的后续作业元素个数。
在装配线上, 根据NHlk值按升序排列所有的作业元素, 对于NHlk值最小的作业元素赋予后续作业量权重Fhk=1, 对于NHlk值次小的作业元素赋予后续作业量权重Fhk=2, 如果作业元素NHlk值相同的, 则被赋予相同的后续作业量权重Fhk。依次类推, 直到所有作业元素都被赋予Fhk。
(3)计算每一个作业元素k的优先关系权重值Rpk。
Rpk=Ftk× Fhk
计算出作业元素的优先关系权重值Rpk后, 列出未分配的作业, 从第一个工作站开始分配, 由当前的工作站决定两条装配线上可利用的作业元素, 生成可利用的作业列表。
检查分配作业的原则是:作业未被分配; 作业没有紧前(紧后)作业, 或者它的所有的前任作业(后任作业)都被分配, 并且作业是按照优先关系图表的前后关系所分配的; 当前工作站的剩余容量(时间)足够执行该作业。
每当一个作业被分配时, 作业列表就会更新一次, 选择另一个新的作业并且分配给当前工作站, 一直持续到当前工作站没有容量(时间)来完成作业。当从优先关系图前部分配作业元素时, 选择优先关系权重最大的作业元素, 当从优先关系图后部分配作业元素时, 选择优先关系权重最小的作业元素, 同时必须兼顾作业元素时间, 使当前工作站的闲置时间尽可能小, 满足目标函数。
装配线平衡问题的效果采用时间损失系数ε 、平衡率BP和平滑系数SI评价[9]。平衡率衡量整个装配过程中装配线平衡和对时间利用效率的指数。时间损失系数衡量装配线对时间的有效利用程度。时间平滑系数衡量装配线负荷的均匀程度。因此, 建立装配线平衡的效果评价数学模型为:
ε =
BP=1-ε
SI=
式中:Tei为每i个工作站被分配作业元素的作业时间总和; Temax为工作站中作业时间总和的最大值。如果最大值等于节拍, Temax取节拍, 系统达到最优; 如果小于节拍, 则还可以继续优化。
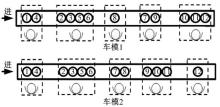
选择两个结构工艺相似的四驱车车模(以下简称车模1、车模2)进行实验, 先产品结构分析, 再装配工艺流程设计, 分别在实验室流水装配线L1和L2上进行装配实验, 测得生产节拍r=10 s。装配作业元素工作内容及时间见表1。车模1、车模2的作业总时间分别为44 s和41 s。
| 表1 作业元素工作内容及时间表 Table 1 Information and time table of job elements |
根据工作内容及工艺流程确定了作业元素及紧前关系, 作业元素流程图见图2。
根据有向网络理论求出作业元素的优先关系权重, 计算结果见表2。
| 表2 作业元素优先关系权重表 Table 2 Priority relation weight table of job elements |
在实验室两条平行直线型装配线上对车模1和车模2进行装配及组织设计。车模1和车模2所需的最低工作站数均为5。根据启发式算法分配作业元素, 其装配线工作站布置及作业元素分配见表3。
直线型装配线设计平面简图见图3。根据装配线的平衡效果评价模型, 综合考虑两条直线型装配线的平衡率BP=85%, 总的闲置时间为15 s。
| 表3 作业元素分配信息及时间表 Table 3 Information and time table of job elements |
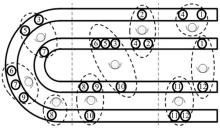
对现有实验室装配线进行改进, 采用两条U型装配线平行布置。根据表2中优先关系权重对装配线分配作业元素。具体分配步骤见表4。从表4中可见, 当前工作站的剩余时间是在每一个作业元素分配到当前工作站后确定。在每个作业元素分配后, 算法从更新后的任务列表中继续挑选和分配下一个作业元素, 持续进行到当前工作站没有足够的剩余时间完成任何一个作业。继续将任务分配到下一设定工作站, 所有作业元素全部分配到两条装配线上。
装配线工作站分配结果见图4, 分成了9个工作站, 装配线的平衡率BP=94.4%, 闲置时间为5 s。
| 表4 分配步骤 Table 4 Assignment steps |
(1)通过实验获得数据, 对装配线平衡建立数学模型, 应用有向网络理论求解, 计算结果正确有效。
(2)装配线平衡方法有效, 引入有向网络实现网络图的程序计算, 为大型网络计算提供了一种新途径, 为企业装配线平衡与优化提供快速计算方法。
(3)双U型装配线设计有效, 与直线型实验室算例比较, 平衡率提高了11.1%, 并节省了1个工作站。不仅节约成本, 而且提高了实验室车模的装配效率, 加快车模零部件流通, 提高了实验室的实验设备的使用效率, 为提高流水装配线平衡提供了有效的新方法。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|