大跨径刚构连续梁桥悬臂施工阶段抗风性能

引用本文

郑一峰, 赵群, 暴伟, 李壮, 于笑非. 大跨径刚构连续梁桥悬臂施工阶段抗风性能. 2018, 48(2): 466-472
ZHENG Yi-feng, ZHAO Qun, BAO Wei, LI Zhuang, YU Xiao-fei. Wind resistance performance of long-span continuous rigid-frame bridge in cantilever construction stage. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 466-472 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170023
Permissions

大跨径刚构连续梁桥悬臂施工阶段抗风性能

郑一峰¹, 赵群¹, 暴伟¹, 李壮², 于笑非³

1.吉林大学建设工程学院,长春 130026

2.东北炼化工程有限公司,吉林省吉林市 132001

3.吉林省林业勘察设计研究院,长春 130021

通信作者:赵群(1987-),男,助理工程师,硕士.研究方向:桥梁与隧道工程.E-mail:zhaoqun@jlu.edu.cn

作者简介:郑一峰(1966-),男,教授,硕士生导师.研究方向:桥梁与隧道工程.E-mail:zhengyf0824@126.com

基金项目:国家自然科学基金项目(51508222)

摘要

依托长白山国际旅游度假区主跨160 m三跨刚构连续梁桥工程,利用Midas Civil软件对依托工程各悬臂施工阶段的动力特性进行计算,分析各个施工阶段的振型和基频的变化规律。根据桥址处的气候条件,计算阵风风速,利用Midas FEA软件CFD模块模拟风场区域,计算桥梁结构最大悬臂状态三分力系数,进而求得静阵风荷载。采用抖振力的实用简化计算方法进行桥梁最大悬臂状态抖振力分析。验算了在风荷载作用下最大悬臂状态结构的安全性。

关键词: 土木工程; 桥梁工程; 抗风性能; 悬臂施工; 静阵风荷载; 抖振力

中图分类号:U414 文献标志码:A 文章编号:1671-5497(2018)02-0466-07

Wind resistance performance of long-span continuous rigid-frame bridge in cantilever construction stage

ZHENG Yi-feng¹, ZHAO Qun¹, BAO Wei¹, LI Zhuang², YU Xiao-fei³

1.College of Construction Engineering, Jilin University, Changchun 130026, China

2.Northeast Refining & Chemical Engineering Co. Ltd., Jinlin 132001, China

3.Forestry Survey and Design Research Institute of Jilin, Changchun 130021, China

Abstract

For the three-span rigid-frame continuous bridge with main span of 160 m in Changbai Mountain International Tourism Resort, the dynamic characteristics in each cantilever construction stage was calculated using Midas Civil software, and the characteristics of the vibration mode and frequency of each construction stage were analyzed. First, according to the climate condition at the bridge site, the gust wind speed was calculated, then the wind field area was simulate using Midas FEA software CFD module. Second, the three component coefficient of the maximum cantilever state of the bridge structure was calculated, and then the static gust was obtained. Finally, the simplified calculation method of buffeting force is adopted to analyze the buffeting force of the bridge under the maximum cantilever state, and the safety of the structure under the maximum cantilever state and wind load was evaluated.

Key words: civil engineering; bridge engineering; wind resistance; cantilever construction; static gust load; buffeting force

Show Figures

0 引言

大跨径刚构连续梁桥多采用薄壁墩结构, 悬臂浇筑法施工, 具有大、轻、柔的特点, 施工过程中要经历体系转换过程。悬臂施工过程中, 风荷载对结构的作用效应比较敏感, 特别是在最大双悬臂状态, 风荷载成为桥梁结构上的支配性荷载^[1]。当较强风速来临时, 对桥梁结构产生一定的升力、阻力以及扭矩, 致使桥梁结构发生弯曲或扭转振动, 甚至导致桥梁墩底或主梁悬臂根部发生破坏而丧失使用功能。因此, 大跨径刚构连续梁桥施工阶段必须进行抗风安全性分析。

目前, 国内外规范^{[2, 3, 4, 5]}对桥梁悬臂施工阶段抗风设计的内容做了比较详细的规定。在横桥向静阵风荷载计算方面, 中国、美国、日本、英国规范给出的公式形式基本上一样, 都考虑了风场因素、阵风风速、桥梁结构参数的影响。在结构惯性动力作用分析方面, 中国、日本规范给出了较为详细的计算方法及相应公式, 而英国、美国在驰振和涡激共振等方面并未明确说明。同济大学对风荷载的计算分析做了大量工作, 并针对悬臂施工的桥梁给出了风荷载计算方法^{[6, 7]}。

由于风会对结构产生静力和动力作用, 计算分析复杂, 本文结合长白山国际旅游度假区主跨160 m三跨刚构连续梁桥的施工监控工作, 对各节段悬臂施工状态进行风荷载作用效应分析, 并验算了短暂状况结构的安全性。

1 风荷载计算理论

对于刚构连续梁桥来说, 风荷载一般分为3个部分:平均风作用、脉动风的背景作用以及结构惯性动力作用。在各国桥梁抗风规范^{[2, 3, 4, 5]}中, 通常将平均风作用与脉动风的背景作用合并到一起考虑, 称为静阵风荷载。

1.1 静阵风荷载

主梁上的静阵风荷载可表示为:

横向风载:P_H=ρ C_HH(1)

竖向风载:P_V=ρ C_VB(2)

扭转力矩:M=ρ ²C_MB²(3)

式中:ρ 为空气密度; V_d为基准风速, 与基本风速、高度及地面粗糙程度有关; C_H为主梁的横向力系数亦称阻力系数; C_V为主梁的竖向力系数; C_M为主梁的扭转力矩系数; B、H分别为主梁宽度和高度。

C_H、C_V、C_M合称为三分力系数, 一般需由风洞试验测得, 也可采用计算流体力学方法模拟风场求得。

对于桥墩来说, 风荷载计算同桥梁主梁阻力计算方法相似, 可表示为:

F_H=ρ C_HA_n(4)

式中:V_g为静阵风风速, 由基准高度处的风速乘以静阵风系数求得; A_n为桥墩顺风向投影面积。

1.2 结构惯性动力作用

结构惯性动力作用指结构抖振时所产生的惯性力, 即抖振力。我国规范采用抖振反应谱计算方法, 计算繁琐且主要针对斜拉桥和悬索桥。对等长双悬臂施工桥梁, 现多采用刘志刚、陈艾荣提出的关于抖振力的实用计算方法^[6]。

对于第i阶振型, 结构单位长度共振响应风荷载为:

P_R_i(x)=g_R_im(x)σ _a_i(x) (5)

式中:m(x)为质量分布函数; g_Ri为共振相应对应的峰值因子; σ _a_i(x)为第i阶振型的加速度响应均方差。

g_R_i= $\begin{matrix} \sqrt[]{1.175 + 2 \ln (600 n_{i})} \end{matrix}$ (6)

式中:n_i为第i阶振型的固有频率。

σ _ai(x)²= $\begin{matrix} \frac{4 {\overset{̅}{p}}^{2} {I_{u}}^{2} {φ_{i}}^{2} (x) {γ_{i}}^{2}}{M_{i}^{* 2}} \end{matrix}$ (2π n)⁴ $\begin{matrix} {|H_{i (n)}|}^{2} \end{matrix}$ · $\begin{matrix} \frac{S_{u} (n)}{{σ_{u}}^{2}} \end{matrix}$ (n)(n)dn(7)

式中: $\overset{̅}{p}$ 为平均风荷载; I_u= $\begin{matrix} \frac{1}{lnz / z_{0}} \end{matrix}$ 为紊流度, z₀为地形粗糙高度; γ _i= $\begin{matrix} \int_{0}^{l} \end{matrix} \begin{matrix} |φ_{i} (x)| \end{matrix}$ dx, φ _i(x)为第i阶振型函数; $M_{i}^{*}$ = $\begin{matrix} \int_{0}^{l} \end{matrix}$ m(x)(x)dx对应于第i阶阵型的广义质量; $\begin{matrix} {|H_{i (n)}|}^{2} \end{matrix}$ 为机械导纳函数, 是结构振动对荷载响应放大的物理表达; S_u(n)为水平风谱, 本文取为Simiu给出的沿高度变化的风谱 $\begin{matrix} \frac{n S_{u} (n)}{u^{2}} \end{matrix}$ = $\begin{matrix} \frac{200 f}{{(1 + 50 f)}^{\frac{5}{3}}} \end{matrix}$ , f=nz/U, z为桥梁高度; σ _u为脉动风风速的根方差; (n)为联合接收函数, 其表达式为:

(n)= $\begin{matrix} \frac{1}{γ_{i}^{2}} \end{matrix} \begin{matrix} \int_{0}^{l} \end{matrix} \begin{matrix} \int_{0}^{l} \end{matrix}$ ψ (x₁, x₂, n)φ _i(x₁)· φ _i(x₂)dx₁dx₂(8)

(n)为桥梁截面的气动导纳, 对于扁平截面一般近似取为Sears函数(n)=, 或偏保守地取为 1。

在实际工程中, 高阶振型对结构的影响比较小, 因此忽略一些次要的影响因素, 主要考虑一阶振型时风荷载对结构的影响, 令:

$\begin{matrix} μ (x) = m (x) φ_{1} (x) \int_{0}^{l} |φ_{1} (x)| dx / \end{matrix} \begin{matrix} \int_{0}^{l} \end{matrix}$ m(x)(x)dx(9)

则共振响应风荷载可表示为:

P_R1(x)=g_R1m(x)σ _a_i(x)=2g_R1I_uμ (x)× $\begin{matrix} \sqrt[]{\int_{0}^{\infty} {(2 πn)}^{4} {|H_{i (n)}|}^{2} \frac{S_{u} (n)}{σ_{u}^{2}} J_{i}^{2} (n) dn} \end{matrix}$ (10)

令:

R₁=(2π n)⁴ $\begin{matrix} {|H_{i (n)}|}^{2} \end{matrix} \begin{matrix} \frac{S_{u} (n)}{σ_{u}^{2}} \end{matrix}$ (n)dn (11)

R₁为惯性风荷载系数, 可简化为:

R₁=S₁E₁/ $\begin{matrix} {\tilde{ζ}}_{1} \end{matrix}$ (12)

S₁=(n₁)(n₁) (13)

E₁= $\begin{matrix} \frac{26.2 f_{1}}{(1 + 50 f_{1})^{\frac{5}{3}}} \end{matrix}$ (14)

f₁=n₁z/ (15)

式中: $\begin{matrix} {\tilde{ζ}}_{1} \end{matrix}$ 为结构阻尼比和气动阻尼比之和。

$\begin{matrix} {\tilde{ζ}}_{1} \end{matrix}$ =(1+ $\begin{matrix} \frac{ρ \overset{̅}{U} C_{d} A}{2 m ζ_{s} ω_{1}} \end{matrix}$ )ζ _s(16)

式中:C_d为线状结构断面的阻力系数; A为截面高度; ζ _s为结构阻尼比。

P_R1(x)=m(x)σ _a_i(x)=2g_R1I_uμ (x) $\begin{matrix} \sqrt[]{S_{1} E_{1} / {\tilde{ζ}}_{1}} \end{matrix}$ (17)

2 悬臂结构短暂状况风荷载分析

2.1 背景工程概况

长白山国际旅游度假区桥梁地处吉林省抚松县松江河镇。该地区年平均风速为2.9 m/s, 年最大风速20 m/s, 春夏盛行西南风, 秋冬盛行西北风。桥梁地处严寒地区, 冬季温度较低。

桥梁全长409 m, 主跨为90 m+160 m+90 m的三跨刚构连续梁桥。主桥断面采用单箱单室截面, 其中中支点梁高9.6 m, 跨中和边支点梁高3.2 m, 顶板宽16.6 m, 底板宽9.0 m。桥墩采用双薄壁墩, 高度26 m, 宽度9 m, 厚度2.6 m。主桥采用悬臂浇筑法施工。该桥是目前东北地区跨径最大的刚构连续梁桥。

该桥于2013年4月开始施工主梁0号块, 之后在“ T” 构两侧逐段浇筑各节段, 2013年11月施工至9号块。经过5个月的冬休期, 该桥于2014年4月复工, 于2014年10月竣工。竣工后对其进行了静载检测试验, 结果表明桥梁性能达到设计要求。

2.2 结构自振特性分析

采用Midas Civil软件对桥梁结构悬臂施工全过程进行动力特性分析。模型采用平面杆单元模拟结构, 最大悬臂状态分散为52个单元, 见图1。结果表明, 随着悬臂长度增加, 结构基频呈现出逐渐减小的趋势, 表明结构刚度逐渐变小, 从1号块阶段到最大悬臂状态, 结构基频减小幅度为77.1%, 据此仅对最大悬臂状态下的结构进行分析即可。结构最大悬臂状态下前5阶结构基频及变形形态见表1。

	Figure Option View Download New Window
	图1 模型单元划分图Fig.1 Model cell partition graph

表1 最大悬臂状态前5阶自振频率及变形形态 Table 1 The first 5 order natural frequencies and deformation shapes of maximum cantilever state

2.3 静阵风荷载计算分析

利用Midas FEA软件CFD模块模拟风场区域, 计算结构最大悬臂状态不同截面位置的风速分布从而得到三分力系数, 进而求得静阵风荷载。模型中参数取值如下:空气密度为1.25 kg/m³; 空气黏性系数为1.8 N· s/m²; 声速为340 m/s; 桥墩风速为32.77 m/s; 主梁风速为36.96 m/s; 瑞流强度为0.005; 瑞流黏度比为0.1。其中, 风速取基准风速, 其他参数参照《公路桥梁抗风设计规范》(以下简称《抗风规范》)确定。

主梁的三分力计算中, 以桥梁施工断面为中心, 建立矩形计算区域。流场区域大小取为模型特征长度的30倍。计算区域中来流方向左右面为远场边界, 上下边界为对称边界, 与桥梁截面相邻的边界使用固壁边界。在较小攻角范围内, 三分力系数变化并不大, 故只对0° 攻角作用下桥梁断面进行分析。主梁各阶段截面形式相似, 现给出16号块截面的流场绕流流线分布图, 见图2。由图可知, 绕流流线在主梁的迎风面翼缘处发生分流, 在箱梁截面顶底板及背风面产生涡流, 当尾流距离主梁较远时, 流线又恢复正常。

	Figure Option View Download New Window
	图2 0° 攻角16号块截面绕流流线Fig.2 Flow line of cross section of section 16 of 0 degree angle of attack

0° 攻角时设计风速作用下主梁16号块截面的流场风速分布见图3。风速在主梁截面的影响下分布十分复杂, 由于主梁的阻挡, 在主梁截面顶底板表面及主梁背风面局部区域风速值较小, 在距离主梁顶底板0.5倍梁高区域风速达到最大。

	Figure Option View Download New Window
	图3 0° 攻角顺风向16号块截面风速分布Fig.3 Wind speed distribution along wind direction to section 16 of 0 degree angle of attack

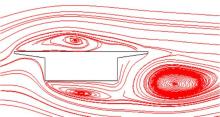
与主梁类似, 对桥墩截面建立流场进行计算, 得到其扰流流线及流场中的风速分布如图4、图5所示。

由图4、图5可见, 由于双薄壁墩截面的阻挡, 风场流线发生改变, 桥墩的背风面形成流动分离作用的漩涡; 在双薄壁墩之间流线基本不受桥墩的影响, 风速值相对较大; 由于桥墩截面的影响, 桥墩背部风速值较小。

	Figure Option View Download New Window
	图4 0° 攻角桥墩截面绕流流线Fig.4 Flow line of cross section of bridge pier of 0 degree angle of attack

	Figure Option View Download New Window
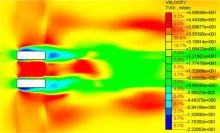	图5 0° 攻角顺风向桥墩截面风速分布Fig.5 Wind speed distribution along the wind direction to bridge pier of 0 degree angle of attack

通过风速分布得到施工阶段各截面三分力系数, 根据式(1)(2)(3)(4)可求得静阵风荷载。特征截面结果见表2。其中, 主梁的阻力系数C_H值与《抗风规范》提供的经验公式计算取值基本一致。

表2 施工阶段特征截面三分力系数及荷载 Table 2 Construction phase characteristic section three component coefficient and load

由表2可知, 主梁三分力系数以及相应荷载大小呈现从支点截面到悬臂端部逐渐减小的趋势。

2.4 抖振力分析

采用式(17)计算抖振力。一阶振型时主梁绕桥墩扭转, 一阶基频为0.456, 在水平风荷载作用下, 本桥一阶振型函数^[7]近似取为:

φ ₁(x)= $\frac{2 x}{L}$ -1

根据式(6)得到共振相应对应的峰值因子g_R1为3.521, 利用MATLAB对本桥悬臂质量分布进行拟合, 得到质量分布函数m(x)表达式为:

m(x)=-0.25x³+32.49x²-245.32x+35034

0≤ x≤ 79

由式(9)得:

μ (x)=-3.39× 10^-⁵· m(x)· φ ₁(x)

桥梁风场信息见表3。

表3 依托工程风场参数 Table 3 Engineering parameters of wind field

将上述风场信息代入式(8)进行积分, 得到(n₁)值为0.153, 本文χ ²(n₁)偏安全考虑取为1, 于是抖振力计算式可化为:

P_r1=-2.19× 10^-⁵· φ ₁(x)· m(x)· $\overset{̅}{P}$

计算时, 各梁段空气阻力按表3中静阵风荷载中的阻力系数取用, 则各悬臂段单位长度抖振力如图6所示。

	Figure Option View Download New Window
	图 6 各悬臂段抖振力Fig.6 Shaking force of each cantilever segment

3 悬臂结构抗风安全分析

对依托工程最大悬臂状态进行抗风分析, 依据《抗风规范》规定, 分析内容包括墩底及悬臂根部的风载内力及应力验算。在最大悬臂状态下, 把静阵风荷载与抖振力荷载相加, 将总的风荷载产生的效应与结构自重产生的效应标准值进行组合, 可以得到墩底及悬臂根部应力与内力值。

3.1 风荷载加载工况

根据抗风规范, 并考虑受力最不利情况, 分4种工况对依托工程进行抗风安全分析。

工况Ⅰ :对T型刚构左、右两端施加对称的风荷载(W_R/W_L=1), 双薄壁墩也施加对称风荷载, 风荷载考虑阻力、升力、扭矩。

工况Ⅱ :考虑风向和风场分布的不均匀性, 对T型刚构左、右两端施加1∶ 0.5的同向风荷载(W_R/W_L=0.5), 双薄壁墩也施加同样比例的风荷载, 风荷载考虑阻力、升力、扭矩。

工况Ⅲ :对T型刚构左右两端施加对称的风荷载(W_R/W_L=1), 双薄壁墩也施加对称风荷载, 风荷载仅考虑横风方向阻力作用。

工况Ⅳ :考虑风向和风场分布的不均匀性, 对T型刚构左、右两端施加1∶ 0.5的同向风荷载(W_R/W_L=0.5), 双薄壁墩也施加同样比例的风荷载, 风荷载考虑横风方向阻力作用。

3.2 悬臂根部抗风安全分析

(1)内力分析

悬臂根部内力结果见表4。

表4 最大悬臂状态各工况荷载组合作用下悬臂根部内力 Table 4 Internal force of cantilever under condition of maximum cantilever state

根据表4结果, 结合静阵风荷载、抖振力荷载单独作用下主梁悬臂根部内力可以得出:风荷载主要引起悬臂根部剪力、扭矩及横桥弯矩的作用, 而对轴力及顺桥弯矩的影响与恒载相比非常小, 轴力及顺桥弯矩主要由恒载引起。经计算本桥抗力大于风荷载产生的内力, 故悬臂根部施工阶段内力满足规范要求。

(2)应力分析

取用主梁悬臂根部截面4个节点应力进行分析, 计算结果见表5。

表5 最大悬臂状态各工况荷载组合作用下悬臂根部应力 Table 5 Cantilever root stress under condition of maximum cantilever state MPa

由表5可知, 悬臂根部各节点受力均为压应力, 且顶板压应力大于底板压应力, 在各工况荷载组合作用下, 悬臂根部顶板压应力最大值为12.497 MPa, 底板压应力最大值为8.182 MPa, 压应力值满足短暂状况应力验算要求。

3.3 墩底抗风安全分析

(1)内力分析

根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》, 求得墩底截面抗剪承载力V_u=31248.1 kN, 抗扭承载力T_u=35840 kN· m。墩底截面内力结果见表6。

表6 最大悬臂状态各工况荷载组合作用下桥墩墩底内力 Table 6 Internal force of pier bottom under condition of maximum cantilever state

在桥墩底部的内力分析中, 抗风分析主要关心风荷载作用引起的墩底剪力及扭矩的大小。由墩底内力计算结果可知, 最大悬臂状态风荷载引起的墩底最大剪力为2764.6 kN; 风荷载引起的墩底最大扭矩为6147.2 kN· m, 均小于截面抗力, 桥墩内力处于安全状态。

(2)应力分析

取用墩底截面4个节点应力进行分析, 结果见表7。

表7 最大悬臂状态各工况荷载组合作用下桥墩墩底应力 Table 7 Pier stress at bottom of bridge under condition of maximum cantilever

在各工况荷载组合作用下, 墩底各节点受力始终为压应力, 压应力最大值为4.523 MPa, 压应力值满足短暂状况应力验算要求。

4 结论

(1)对各施工节段动力特性进行分析, 随着悬臂长度增加, 结构基频呈现出逐渐减小的趋势, 表明结构刚度逐渐变小, 即最大悬臂状态为桥梁抗风分析的最危险阶段。

(2)采用计算流体力学方法分析箱型断面静力三分力系数, 主梁的阻力系数C_H值与《抗风规范》提供的经验公式计算数值基本一致。验证了计算流体力学方法模拟风场分析的可靠性。在缺乏风洞试验的条件下, 可以采用该方法进行截面流场分析。

(3)桥梁结构最大悬臂状态下对主梁和桥墩进行抗风分析, 计算结果表明, 桥梁主梁和桥墩应力、承载能力和稳定性均通过验算, 施工过程中, 抗风性能良好。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	项海帆. 现代桥梁抗风理论与实践[M]. 北京: 人民交通出版社, 2005. [本文引用:1]
[2]	JTG/TD60-01-2004. 公路桥梁抗风设计规范[S]. [本文引用:2]
[3]	BSI. Steel, Concrete and Composite Bridges: Part2. Specification for Loads[M]. London: British Stand ards Institution, 2006. [本文引用:2]
[4]	AASHTO. LRFD Bridge Design Specifications[M]. Washington DC: Ameriean Assoeiation of State Highway and Transportation Officials, 2005. [本文引用:2]
[5]	Sato H. Wind-resistant design manual for highway bridges in Japan[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91: 1499-1509. [本文引用:2]
[6]	刘志刚, 陈艾荣. 等长双悬臂等效风荷载实用计算方法[J]. 同济大学学报, 2002, 30(5): 599-603. Liu Zhi-gang, Chen Ai-rong. A practical method for calculating equivalent wind load of equal length double cantilever[J]. Journal of Tongji University, 2002, 30(5): 599-603. [本文引用:2]
[7]	Mendes P A, Branco F A. Unbalanced wind buffeting effects on bridges during double cantilever erection stages[J]. Wind and Structures, 2001, 4(1): 45-62. [本文引用:2]

2005

0.0

... 悬臂施工过程中,风荷载对结构的作用效应比较敏感,特别是在最大双悬臂状态,风荷载成为桥梁结构上的支配性荷载^[1] ...

0.0

... 目前,国内外规范^[2,3,4,5]对桥梁悬臂施工阶段抗风设计的内容做了比较详细的规定 ...

... 在各国桥梁抗风规范^[2,3,4,5]中,通常将平均风作用与脉动风的背景作用合并到一起考虑,称为静阵风荷载 ...

2006

0.0

... 目前,国内外规范^[2,3,4,5]对桥梁悬臂施工阶段抗风设计的内容做了比较详细的规定 ...

... 在各国桥梁抗风规范^[2,3,4,5]中,通常将平均风作用与脉动风的背景作用合并到一起考虑,称为静阵风荷载 ...

2005

0.0

... 目前,国内外规范^[2,3,4,5]对桥梁悬臂施工阶段抗风设计的内容做了比较详细的规定 ...

... 在各国桥梁抗风规范^[2,3,4,5]中,通常将平均风作用与脉动风的背景作用合并到一起考虑,称为静阵风荷载 ...

2003

0.0

... 目前,国内外规范^[2,3,4,5]对桥梁悬臂施工阶段抗风设计的内容做了比较详细的规定 ...

... 在各国桥梁抗风规范^[2,3,4,5]中,通常将平均风作用与脉动风的背景作用合并到一起考虑,称为静阵风荷载 ...

2002

0.0

. 2002, 30(5):599-603 DOI:doi:10.3321/j.issn:0253-374X.2002.05.014

A practical method for calculating equivalent wind load of equal length double cantilever

等长双悬臂等效风荷载实用计算方法

Liu Zhi-gang , Chen Ai-rong.

刘志刚, 陈艾荣

一些桥梁在双悬臂施工状态下的等效风荷载问题比较特殊,以往的文献对其讨论很少.对这种情况下等效风荷载的计算方法进行了研究,给出了简洁的实用计算公式.实例分析和比较表明,给出的实用计算公式具有很好的精度,无需查阅图表和插值,适于工程应用,并可为我国正在编写的桥梁抗风设计规范提供参考.

... 同济大学对风荷载的计算分析做了大量工作,并针对悬臂施工的桥梁给出了风荷载计算方法^[6,7] ...

... 对等长双悬臂施工桥梁,现多采用刘志刚、陈艾荣提出的关于抖振力的实用计算方法^[6] ...

2001

0.0

... 同济大学对风荷载的计算分析做了大量工作,并针对悬臂施工的桥梁给出了风荷载计算方法^[6,7] ...

... 456,在水平风荷载作用下,本桥一阶振型函数^[7]近似取为: ...