引用本文
李龙, 张幽彤, 左正兴. 变负载控制在自由活塞内燃发电机的缸压控制中的应用. 2018, 48(2): 473-479
LI Long, ZHANG You-tong, ZUO Zheng-xing. Application of variable-load control in cylinder pressure control of free-piston engine generator. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 473-479  
Doi:10.13229/j.cnki.jdxbgxb20161283
Permissions
Copyright©2018, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
变负载控制在自由活塞内燃发电机的缸压控制中的应用
李龙, 张幽彤, 左正兴
北京理工大学 机械与车辆学院,北京 100081

作者简介:李龙(1976),男,工程师,博士.研究方向:新能源汽车.E-mail:voyage_lee@163.com

基金项目:国家自然科学基金项目(51675043)
摘要

为有效控制自由活塞内燃发电机的缸压,提出了变负载控制约束活塞运动的方法。通过构造可变等效负载实现对系统回路总阻抗的控制,回路电流因此发生变化,使作用在发电机动子上的电磁阻力也发生改变,由于发电机动子和活塞刚性连接,从而实现对活塞运动的约束。为使电磁力能按照期望的规律变化,研究中设计了变负载控制的闭环控制策略。仿真结果表明,应用该控制策略的变负载控制可以使活塞运动趋于稳定,从而实现对缸压的稳定控制。

关键词: 动力机械工程; 自由活塞内燃发电机; 变负载控制; 等效负载; 缸压控制
中图分类号:TK441 文献标志码:A 文章编号:1671-5497(2018)02-0473-07
Application of variable-load control in cylinder pressure control of free-piston engine generator
LI Long, ZHANG You-tong, ZUO Zheng-xing
School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China
Abstract

In order to control the cylinder pressure of free-piston engine generator, a variable-load control method is proposed. The control of the total impedance of the system circuit is achieved by the construction of a variable equivalent load, so that the loop current is changed, and then the electromagnetic resistance acting on the mover changes. In order to make the electromagnetic force change in accordance with the expected law, a closed-loop control strategy is designed. Simulation results show that, using this control strategy, the proposed variable-load control method can stabilize the piston motion, thus achieving a stable cylinder pressure.

Key words: power machinery and engineering; free-piston engine generator; variable-load control; equivalent load; cylinder pressure control
0 引 言

自由活塞内燃发电机(FPEG)是近年兴起的新型动力机械, 具有结构简单、重量轻、体积小、压缩比可变、热效率高等优点, 吸引了众多学者进行深入研究。但由于该类发动机没有曲柄连杆和飞轮装置的约束, 使其难以约束活塞的运动状态, 影响发动机稳定工作[1, 2, 3, 4]。缸压的稳定程度是衡量FPEG运行状态好坏的一个重要指标, 所以如何有效稳定缸压就成了解决FPEG稳定运行的关键问题, 世界多所大学和研究机构都开展了相关研究。

1991年, 加拿大里贾纳大学Josrph Kos[5]以专利形式提出了单气缸和对置气缸自由活塞内燃发电机的概念, 之后多个研究机构围绕FPEG展开多方向的研究, 稳定运行控制是其中一个重要研究方向[3, 4, 6, 7]。捷克理工大学从2003年开始Linear Combustion Engine (LCE)项目研究[8], 设计了完整的数学模型和控制策略, 并先后建造了两台实验样机。研究控制点火位置、喷油时刻等因素对LCE稳定运行的影响。研究发现, 精确控制活塞运动是技术难点之一。从2003年起, 英国纽卡斯尔大学开始对自由活塞发动机进行了性能和运动控制的研究。Mikalsen等[3, 6, 7, 9]对活塞运动控制进行了理论分析, 提出了一种基于上止点(TDC)位置偏差监测的控制策略, 利用上一周期活塞的运动状态推算目标上止点的位置, 并做出相应控制操作, 实现对活塞运动的控制。北京理工大学从2005年开始进行相关研究, Jia等[10, 11, 12, 13]通过仿真和台架试验对FPEG的特性进行了大量深入研究工作, 对FPEG的启动过程控制以及稳定运行控制的研究取得了大量的研究成果。

多数研究中, 主要探讨点火时刻、喷油量和喷油时刻对FPEG运行的影响[4, 7, 11, 14]。这些控制方法在很大程度上能够有效改善FPEG的运行状态, 但由于燃烧波动的存在, 使上述手段对燃烧发生后的活塞运行缺乏有效控制, 导致活塞运行上止点控制精度不足, 压缩比循环变动大, 缸内峰值压力循环变动大, 使发动机不能连续稳定运行。传统发动机的活塞受到曲柄连杆和飞轮装置的约束, 燃烧波动基本不影响压缩比的变化, 对下一个循环影响有限。受曲柄连杆和飞轮装置的启发[15], 为自由活塞发动机构建一个可以发挥类似作用的约束力, 可以使活塞运动在燃烧结束后仍然能受到有效约束, 从而稳定FPEG的运行。本文从对置双气缸FPEG的工作原理上入手, 分析了对FPEG稳定运行的影响因素, 选择电磁力作为控制手段, 构造等效负载, 通过变负载控制实时调节活塞受到的电磁力, 使其与活塞运动状态匹配, 实现稳定缸压的目的, 从而实现FPEG的稳定运动。通过搭建Simulink模型对变负载控制的效果进行了验证。

1 原理分析及控制策略
1.1 FPEG的工作原理

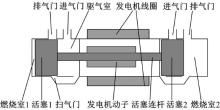
对置双气缸FPEG的主要结构如图1示意。图中燃烧室1、2和活塞1、2分别置于发动机两端, 空燃混合气交替进入燃烧室1和2。燃烧室1燃烧做功的同时, 燃烧室2开始为点火做准备。当活塞2压缩混合气到达点火位置时, 燃烧室2内的气体被点燃做功, 活塞被推动向压缩的相反方向运动, 实现活塞组件的换向运动。两边燃烧室依次循环工作, 推动发电机动子在发电机线圈中做往复运动, 线圈连续切割磁力线产生感生电动势, 在与负载构成的回路连通的情况下形成电流输出, 至此就实现了热能-机械能-电能的转换, 并通过电能驱动负载实现对外输出能量[16, 17]。

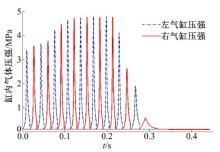
图1 对置双气缸自由活塞内燃发电机结构示意Fig.1 Structure of opposed twin-cylinder FPEG

FPEG没有曲柄连杆和飞轮装置, 活塞在燃气推动下自由运动, 当燃烧状态发生变化时, 就会表现在活塞运动速度和上止点的变化上, 进而影响下一个循环的燃烧条件, 导致燃烧状态的不稳定。同时, 对置两缸的作用力通过活塞组件直接耦合, 在一端发生燃烧波动时必然影响到对端, 往复循环, 使缸内燃烧条件急剧恶化, 从而导致发动机失火或撞缸停车。图2示意了燃烧波动引起的失火停车现象。

图2 燃烧波动及其影响Fig.2 Combustion fluctuations and its effects

图2中波形表明, 在燃烧异常时导致气缸压强下降。从第8个循环的前半周期(点线)开始, 燃烧波动使气缸压强小于正常值, 导致活塞运动受到影响, 在第9个循环的后半周期, 活塞没有足够能量运动到对端的点火位置(实线) 导致失火停车。

1.2 变负载控制原理

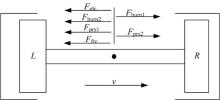
图3为活塞组件的受力情况。

图3 活塞组件的受力Fig.3 Forces acting on piston device

通过牛顿第二定律可以给出活塞组件的动力学方程:

m· d2xdt2= Fburn1-Fburn2+ Fprs2-Fprs1-Felc-Ffrc (1)

式中:m为活塞组件质量; Fburn1、Fburn2分别为两侧燃烧室内的气体压力; Fprs1、Fprs2分别为两侧驱气室的气体压力; Felc、Ffrc分别为电磁阻力和动子组件摩擦力。

活塞组件在从上止点运动到下止点(BDC)时, 能量方程如下:

Eburn1=Eburn2+Epre+Eelc+Efrc (2)

Eburn1=∫ Fburn2+Fpre+Felc+Ffrcdx (3)

式中:Eburn1为燃烧室1燃烧释放的总能量(假设燃烧室1燃烧放热, 燃烧室2压缩气体做功); Eburn2为燃烧室2压缩混合气体消耗的能量; Epre为两侧驱气室压缩空气消耗能量的代数和; Eelc为发电机吸收的能量; Efrc为所有阻力消耗的能量。

为了简化分析, 式(2)忽略了由于传热和漏气等因素带来的能量损失。由于放热异常使Eburn1减小, 式(3)右侧的总和相应减小, 在内燃机和发电机参数不变的情况下, 位移参数x的增量必然减小, 当活塞位移x不能到达点火位置时, 发动机失火停车, 如图2所示。该能量关系如下:

Eburn2+Epre+Eelc+Efrc=Esuit(4)

Eburn1> Esuit(5)

Eburn1=Esuit(6)

Eburn1< Esuit(7)

Esuit是实现等式平衡需要的参考能量, 是预设值, 在确定后由式(4)左面的4个参数组合得到。式(6)是期望的状态, 实际运行中式(5)(6)(7)的情况都会出现。当不等式(5)(7)所表达的关系差值较大时, 就会发生撞缸停车和失火停车的情况。燃烧波动是不可避免的, 如果在燃烧波动发生时, Esuit能跟随波动正向调节, 使式(6)继续成立, 则可以抵消波动带来的缸内压强的变化。

1.3 气缸压强控制策略

由前述知, 等式(4)左侧的4个参数分别由Fburn2、Fpre、和Ffrc和Felc对位移积分得到。其中, Fburn2、Fpre、和Ffrc是由FPEG系统结构特征决定的力, 在FPEG装配完毕后就确定了(忽略温度变化等因素带来的影响); Felc是在感生电动势的驱动下, 电流流过发电机线圈时产生电磁力。感生电流大小由回路总阻抗决定。因为电机的内部阻抗已经确定, 因此可以调节外部负载阻抗来影响电流, 间接控制Felc的大小。从式(3)可知, 当发生燃烧波动时, Felc (Eelc)跟随Eburn1同向变化, 就可以继续保持式(6)平衡。使用实时调节等效负载大小的方法可以实现Felc跟随燃烧波动同向变化, 电磁力增量补偿了燃烧波动的能量增量, 由此实现气缸压强的稳定。

Felc可以由下式计算得到:

Felc= Kf·KRr+RL+j·L (8)

式中:Kf为发电机推力系数; Rr为发电机阻抗; RL为负载阻抗; L为发电机线圈电感; K为反电动势系数。

通过式(8)可以看出, 当外接负载阻抗RL发生变化时会引起Felc发生变化, 这是希望得到的效果。令:

Kmag= Kf·KRr+RL+j·L=Kf· K· Kp(9)

式中:Kp为调节系数, 是RL的函数。Kp通过对比当前缸压和目标缸压的差值进行负反馈调节, 使Kmag表征的发电机动子速度和电磁力之间的关系朝着减小缸压偏差的方向发生变化, 通过PI控制器使控制目标快速实现。

2 等效负载电路及仿真验证
2.1 等效负载电路

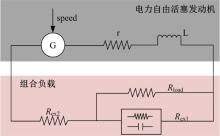
通过上述分析可知, 只要改变“ 发电机-负载” 回路的总阻抗就能实现调节Felc的目的, 由此, 可以构造如图4所示的等效负载电路。

图4 FPEG-负载系统等效电路Fig.4 FPEG-load system equivalent circuit

图4中G为发电机, r为发电机等效内阻, L为发电机线圈电感, 这三部分构成发电机等效模型。Rload为实际负载, 设定为阻性负载。Rex1为并联可控负载元件, 由等效阻性元件和超级电容组成, 用来向下调节负载总阻抗。该支路的分流电量被超级电容存储, 在控制策略调度下, 该电量会在Rload和Rex1构成的回路中消耗, 由于Rex1是等效阻抗, 不实际消耗能量, 所以, 电能最终被Rload吸收。为简化分析, 认为该电容足够大, 在接入回路时的容抗足够小, 忽略容抗, 则Rex1简化为纯电阻特性。Rex2是串联可控负载元件, 用于向上调节总阻抗。由于Rex1、Rex2是等效负载元件, 是通过控制电压与电流的关系等效出阻抗特性, 不实际消耗电能(事实上存在mΩ 级的电阻, 消耗很小的一部分电能), 理想状态下, 发电机对外输出的电能最终都被Rload吸收。

忽略活塞带动发电机线圈运动时的摩擦、热耗等能量损失, 则电磁力做功等于电流做功:

Felc· dx=i2· Rload∥Rex1+Rex2· dt (10)

在应用中, Rex1和Rex2配合工作。当减小负载功率时, 需要向上调节阻抗, Rex1断路, 电流流经Rload、Rex2构成的串联回路。此时调节Rex1实现负载总阻抗的增大。等式(10)可以简化为:

Felc· dx=i2· Rload+Rex2· dt (11)

当增大功率时, 需要向下调节阻抗, Rex2短路, 电流流经Rload、Rex1构成的并联回路。此时调节Rex2实现负载总阻抗的减小。等式(10)可以简化为:

Felc· dx=i2· Rload∥Rex1· dt (12)

2.2 建模与仿真

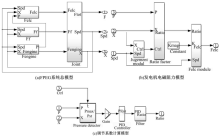
图5(a)是FPEG系统总模型。其中, “ Felc” 模块是发电机电磁阻力模块, 针对变负载控制研究使用, 对外输出电磁阻力; “ Ff” 是摩擦力模块, 输出等效摩擦阻力; “ Fengine” 是FPEG的内燃机模块, 输出驱动力; “ Joint” 是汇聚运算模块, 计算合力作用下的活塞位置、速度参数。其中“ Ff” , “ Fengine” , “ Joint” 三个模块参照已有研究成果[18]搭建, 本文不展开研究, 只使用其有效性结论。图5(b)是发电机电磁阻力模型, 是“ Felc” 模块的展开。其中“ Judgment module” 是气缸压强测量决策模块, 判断活塞运动方向和位置, 并按照预定策略给控制信号到“ Ratio factor” 模块。“ Ratio factor” 模块用于计算在峰值缸压P的反馈下等效负载的响应值, 并以调节系数的方式输出给“ Felc module” 模块, 通过和额定负载系数Kmag以及速度参数“ Spd” 共同运算得到受控制的电磁力Felc。精确控制该电磁力的大小是控制活塞运动状态的关键。图5(c)是“ Ratio factor” 模块的展开, 模块内部主要由“ Pressure detector” 模块、PI控制器模块和系数滤波器“ Filter” 构成。其中“ Pressure detector” 对采样压强进行偏差计算, 计算结果送入PI控制器后对外输出调节系数。为了保证系数在系统可以操作的范围, 增加了“ Filter” 模块进行安全控制。

图5 Simulink模型Fig.5 Simulink model

验证目标FPEG的主要参数如下:缸径为0.034 m, 有效行程为0.02 m, 最大行程为0.04 m, 重叠距离为0 m, 活塞质量为2.5 kg, 进气压强为0.1013 MPa, 进气温度为313 K, 燃料类型为汽油。

通过以上参数可计算出该模型样机的有效气缸容积为1.82× 10-5 m3。按照油气混合比(1∶ 14.7)计算, 单侧气缸在理想状态下可注入热量67.2 J。受到扫气损失、泄露损失和燃烧效率等因素的影响, 燃料的实际放热量小于67.2 J, 因此选择23.5、30.3、37、43.7 J来模拟4种不同的燃烧放热结果, 通过对比来验证在不同燃烧条件下变负载控制对稳定缸压的控制效果。设定目标峰值缸压为5 MPa, 起始负载系数为160 [N· (m· s-1)-1], 仿真结果如图6所示。

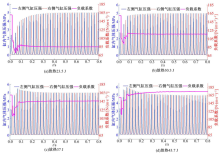
图6(a)是单侧气缸一次释放23.5 J热量的情况。在第12个循环, 缸内峰值压强到达了预期值5 MPa, 偏差< 2%(设定的允许偏差), 负载系数自动调节到85 [N· (m· s-1)-1], 压缩比稳定在8.5。此后, 负载系数随峰值缸压的循环变动做微小调整; 图6(b)是单侧气缸一次释放30.3 J热量的情况。在第9个循环, 缸内峰值压强到达了预期值, 偏差< 2%, 负载系数自动调节到116 [N· (m/s-1)-1], 压缩比稳定在7.6。此后, 负载系数随峰值缸压的循环变动做微小调整; 图6(c)是单侧气缸一次释放37 J热量的情况。在第10个循环, 缸内峰值压强到达了预期值, 偏差< 2%, 负载系数自动调节到146 [N· (m· s-1)-1], 压缩比稳定在6.8。此后, 负载系数随缸压的循环变动做微小调整; 图6(d)是单侧气缸一次释放43.7 J热量的情况。在第14个循环, 缸内峰值压强到达了预期值, 偏差< 2%, 负载系数自动调节到174 [N· (m· s-1)-1], 压缩比稳定在6.2。此后, 负载系数随缸压的循环变动做微小调整。

在图6所示的4次仿真中, 每当缸压稳定后, 压缩比也随之稳定。当缸压被控制在一个固定值时(例如5 MPa), 对应不同的燃烧放热条件会有不同的压缩比, 且随着放热量的增加, 压缩比下降, 这是由于更多的放热量可以产生更大的气缸压强, 此时, 只有降低压缩比才能稳定缸压。在变负载控制下, 随着放热量的增加, 控制系统自动调高负载系数, 通过加大对外电能输出来降低活塞的压缩能, 使活塞运动受到约束, 从而实现对缸压的控制, 进而得到稳定的峰值缸压。

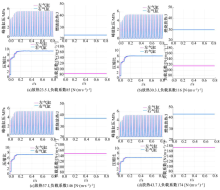
图 6 变负载控制在不同燃烧放热条件下 的缸压控制效果Fig.6 Cylinder pressure control effects of using variable-load control method under different heat release conditions

2.3 验证

由于实验条件的限制, 直接验证存在一定困难, 故借助已经校验过的模型[18], 将前述4种放热条件下仿真得到的负载系数值回代运行, 根据其结果间接验证。图7(a)~(d)显示了与放热量对应的负载系数回代到参考模型中得到的缸压和压缩比曲线。

由图7可见, 在放热量和负载系数都是常数的每一种情况下, 峰值缸压和压缩比都能够逐步上升并达到稳定状态。在4幅图中, 系统达到稳定状态时的峰值缸压均接近于5 MPa, 这与预期的结果相符, 压缩比均略高于变负载控制模型的计算值, 压缩比的变化规律与预期结果相符。参考模型与变负载控制模型的计算数值的偏差是由两个模型在处理阻力损耗和漏气损耗等方面的算法不同引起的, 由于两者偏差较小, 且变化趋势稳定, 因此通过该间接方法可以验证文章所述的变负载控制缸压的方法是有效的。

图7 放热量和负载系数是常数时的缸压和压缩比响应Fig.7 Cylinder pressure and compression ratio response to constant heat release and constant load factor

3 结 论

(1)使用变负载控制可以有效控制FPEG的缸压。对于不同的燃烧放热量, 变负载控制方法能够自动调节负载系数, 使峰值缸压收敛于期望值, 从而实现FPEG对多类型燃料的适用性。

(2)使用变负载控制对缸压进行控制时, 压缩比会随燃烧放热量的增加而降低, 利用该特性可以指导FPEG的设计。

(3)使用变负载控制可以减弱燃烧波动对系统的影响, 从而改善FPEG的运行状态, 使其能够稳定运行。

The authors have declared that no competing interests exist.

参考文献
[1] Mikalsen R, Roskilly A P. A review of free-piston engine history and applications[J]. Applied Thermal Engineering, 2007, 27(14/15): 2339-2352. [本文引用:1]
[2] Clark N N, Nand kumar S, Atkinson C, et al. Operation of a small bore two-stroke linear engine[J]. American Society of Mechanical Engineers, 1998, 31(1): 33-42. [本文引用:1]
[3] Mikalsen R, Roskilly A P. The control of a free-piston engine generator. Part 2: engine dynamics and piston motion control[J]. Applied Energy, 2010, 87(4): 1281-1287. [本文引用:3]
[4] 李庆峰. 自由活塞式内燃发电机的研究[D]. 上海: 上海交通大学机械与动力工程学院, 2011.
Li Qing-feng. Performance analysis of a free piston linerar alternator [D]. Shanghai: College of Power Machinery and Engineering, Shanghai Jiaotong University, 2011. [本文引用:3]
[5] Kos J F. Computer optimized hybrid engine[P]. United States Patent: 5002020, 1991-03-26. [本文引用:1]
[6] Mikalsen R, Jones E, Roskilly A P. Predictive piston motion control in a free-piston internal combustion engine[J]. Applied Energy, 2010, 87(5): 1722-1728. [本文引用:2]
[7] Mikalsen R, Roskilly A P. The control of a free-piston engine generator. Part 1: fundamental analyses[J]. Applied Energy, 2010, 87(4): 1273-1280. [本文引用:3]
[8] Nmeek P, Vysok O. Control of two-stroke free-piston generator[C]∥Proceeding of the 6th Asian Control Conference, Bali, Indonesia, 2006: 18-21. [本文引用:1]
[9] Mikalsen R, Roskilly A P. The design and simulation of a two-stroke free-piston compression ignition engine for electrical power generation[J]. Applied Thermal Engineering, 2008, 28(5/6): 589-600. [本文引用:1]
[10] Jia B, Tian G, Feng H, et al. An experimental investigation into the starting process of free-piston engine generator[J]. Applied Energy, 2015, 157: 798-804. [本文引用:1]
[11] Mao J, Zuo Z, Feng H. Parameters coupling designation of diesel free-piston linear alternator[J]. Applied Energy, 2011, 88(12): 4577-4589. [本文引用:2]
[12] Feng H, Song Y, Zuo Z, et al. Stable operation and electricity generating characteristics of a single-cylinder free piston engine linear generator: simulation and experiments[J]. Energies, 2015, 8(2): 765-785. [本文引用:1]
[13] Jia B, Zuo Z, Tian G, et al. Development and validation of a free-piston engine generator numerical model[J]. Energy Conversion and Management, 2015, 91: 333-341. [本文引用:1]
[14] Mikalsen R, Roskilly A P. A computational study of free-piston diesel engine combustion[J]. Applied Energy, 2009, 86(7/8): 1136-1143. [本文引用:1]
[15] Johansen T A, Egeland O, Johannessen E A, et al. Free-piston diesel engine timing and control- toward electronic cam- and crankshaft[J]. IEEE Transactions on Control Systems Technology, 2002, 10(2): 177-190. [本文引用:1]
[16] Jia B, Zuo Z, Feng H, et al. Development approach of a spark-ignited free-piston engine generator [C]∥ SAE Technical Paper, 2014 -01-2894. [本文引用:1]
[17] Xiao J, Li Q, Huang Z. Motion characteristic of a free piston linear engine[J]. Applied Energy, 2010, 87(4): 2388-1294. [本文引用:1]
[18] 毛金龙. 自由活塞直线发电机工作过程数值仿真及实验研究[D]. 北京: 北京理工大学机械与车辆学院, 2011.
Mao Jin-long. Numerical simulation and experimental analysis of free-piston linear alternator [D]. Beijing: College of Mechanical Engineering, Beijing Institute of Technology, 2011. [本文引用:2]