作者简介:孟育博(1986-),男,博士研究生.研究方向:柴油机喷油系统控制.E-mail:myb0201@126.com
针对所开发的压电式共轨喷油器,采用压电执行器作为驱动元件,为了更好地对这类执行器的潜力进行开发,试验研究了压电执行器在准静态条件下的热-电-机械耦合特性。结果表明:在200~1200 N范围内,位移随着预紧力呈先增大后减小趋势;在25~80 ℃范围内,位移整体呈增大趋势,但随着温度升高,增长趋势逐渐变缓。一个包括压电堆迟滞特性和温度影响的数学模型被用来对试验结果进行模拟,仿真与试验结果具有良好的一致性。
To develop a piezoelectric common rail injection, the piezoelectric stack actuator was selected as the driving element. In order to exploit the potential of this kind actuation, the thermo-electro-mechanical behavior of the piezoelectric actuator was investigated by experiment, with maximum voltage of 150 V under different mechanical loads and different temperatures. Results show that, as the load increases from 200 N to 2000 N, the displacement increases first, and then decreases. In the temperature range of 25?C to 80 ?C, the displacement increase with the temperature, but this trend gradually slows down. A mathematical model based on the hysteresis and temperature effects is applied to simulate the experiment data, and the simulation results show reasonable agreement with the experiment results.
压电陶瓷元件由于压电效应和逆压电效应而作为传感器或执行器被广泛应用于工业中。同时这些驱动由于响应快、输出力大和紧凑设计等特性被用于现代发动机喷油系统中, 基于压电堆的喷油器被用于燃油喷射阀的开启与闭合[1, 2]。由于压电执行器相比于传统的电磁阀执行器具有更快的响应速度, 因此能够对多次喷射之间的时间间隔进行精确控制, 有助于降低排放。同时, 基于压电堆的喷油器能够提高喷油压力, 可以达到250 MPa; 喷油压力越高, 喷油量越精确, 燃烧越高效。当压电堆用作执行器应用时, 采用式(1)进行线性压电材料的描述[3]。
S3=
式中:S3为应变; T3为机械应力; E3为电场强度;
由于执行器工作在较宽的工作范围中, 且大部分时间工作在非线性状态, 线性工作方式只占较小的一部分, 因此式(1)不能全面描述执行器的特性[4, 5]。对于压电材料而言, 非线性迟滞现象是其基本特征且对压电执行器的精确控制具有很大的影响, 因此迟滞特性不可忽略。相应的, 由于喷油器处在发动机缸盖十分关键的位置, 因此温度的影响也不可忽略。
压电致动器在正常运行情况下的性能和可靠性是促进压电执喷油器技术进一步发展的关键。因此, 压电执行器的研究得到广泛的关注。应力、温度对压电执行器性能的影响已有相关的研究[6, 7]。在文献[8]中应力和电场的综合效应已经被分析, 文献[9]中温度和电场的综合效应也被研究, 并得出在固定预紧力条件下压电耦合系数的多项式:
式中:E为电场强度; θ 为温度; a0、a1、a2、a3为试验耦合系数。
文献[10]对执行器位移的增加进行试验分析, 而文献[11]对位移的增加尝试从物理的角度进行解释。在压电执行器的实际应用中, 输入场(例如电场、机械场和温度场)都不是恒定的。因此, 在耦合迟滞建模过程中, 需要对材料甚至整个执行器有一个精确的描述。
为了提高压电执行器的控制精度, 国内外学者对压电陶瓷执行器数学模型进行研究。提出了模拟其迟滞特性的Preisash模型、Maxwell模型、Dahl模型和Duhem模型等。
Preisash模型是最常用的数学模型之一[12], 但是存在在线实现复杂的缺点; Maxwell模型存在求解计算过程过于复杂的缺点[13]; Dahl模型参数较多, 参数的辨识过程比较复杂[14]。而Duhem模型是输入信号导数的函数, 模型输出与输入信号的速率相关, 符合压电材料中迟滞非线性的动态特性, 能够更精确地描述压电致动器的迟滞特性[15]。
本文研究了应用于喷油器的压电执行器的迟滞特性。在准静态条件下对压电致动器热-电-机械性能进行测试。在试验的基础上, 对所建立的模型参数进行辨识并进行试验验证。
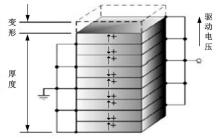
一般而言, 压电执行器产生的最大应变为0.1%~0.15%[16], 且压电堆执行器由许多层压电执行器片组成, 如图1所示, 因此压电堆执行器的位移是单层压电执行器片位移的总和。在本文中, 商业应用的锆钛酸铅压电堆执行器被用于试验研究。执行器使用温度范围为-20~120 ℃, 居里温度为240 ℃。表1显示了用于试验研究的执行器的几何结构和产品性能。
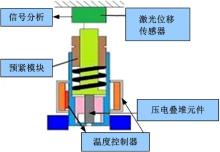
压电堆执行器的测试装置原理图如图2所示, 压电堆执行器固定在预紧力测试装置中, 采用矩形弹簧(47 N/mm)和螺母进行预紧力的施加, 通过旋转螺母改变弹簧的形变来改变预紧力的大小, 同时采用力传感器(量程为0~3 kN, 精度为满量程的0.3%)进行预紧力的测试。预紧力装置固定在夹具上; 加热装置安装在预紧力装置外, 热电偶(量程为-20~200 ℃, 偏差为± 1.5 ℃)用于温度的测量, 温度调节通过PID控制器来完成。采用激光位移传感器(量程± 1 mm, 分辨率0.1 μ m)测量位移, 并把信号传输到处理设备, 用于执行器输出特性的研究。
| 表1 PZT执行器特性 Table1 Characteristics of PZT actuator |
为了研究机械载荷对压电执行器特性的影响, 按照下述测试方法进行测试:①预紧机械载荷从小(例如200 N)到大逐渐增加; ②电压采用单极驱动, 最大电压为150 V; ③测试温度为25 ℃。
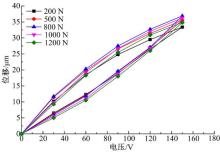
图3为不同机械载荷下的电压-位移曲线, 电压信号频率为5 Hz。由图可以看出, 预紧机械载荷不仅影响压电堆执行器峰值大小, 并且还影响迟滞曲线的形状和面积。由于预紧力能够影响执行器自生热, 因此在设计预紧机械载荷时应当考虑对迟滞曲线形状的影响。压电堆执行器迟滞环所代表的能量正是执行器生热的主要来源。
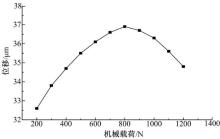
图4中, 峰值位移作为预紧力的函数被记录, 预紧力为[200, 1200] N。最大位移出现在大约800 N。相对于200 N时的位移输出, 800 N时的位移输出增加约4.3 μ m。应当注意的是, 在所给执行器数据中这个值为29 μ m, 也就是预紧力为0 N的值。因此, 这个预紧力数值可以作为压电执行器基础结构优化设计的参考值。
为了评估温度对压电执行器特性的影响, 根据下面的设置进行一系列的评估测试:①采用测试2中所加的预紧力; ②电压采用单极驱动, 最大电压为150 V; ③温度变化从25 ℃到80 ℃。
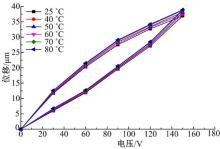
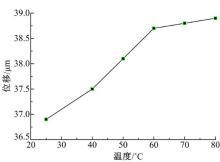
图5是在载荷(预紧力)为800 N、频率为5 Hz、电压从0到150 V时, 不同温度下的电压-位移曲线。温度对压电堆执行器的影响主要体现在, 在一定的范围内压电堆执行器随着温度的升高总体呈现上升的趋势。为了定量研究温度对位移输出的影响, 特别把在电压为150 V时不同温度下的位移值提取出来, 如图6所示。
由图6可以看出, 在温度从25 ℃到增加到60 ℃时, 位移增加约为0.6 μ m, 从60 ℃到增加到80 ℃时, 位移增加约为0.1 μ m。因此, 压电执行器在从25 ℃到60 ℃时, 温度对位移输出的影响较大; 从60 ℃变化到80 ℃过程中, 影响逐渐减小。而应当注意的是, 厂家所提供的是常温下预紧力为零时获得的位移。
Duhem模型是一种动态模型, 该模型最大的优点就是具有明确的数学表达式, 适当地调整模型参数可以准确反映不同迟滞非线性, 因此选用Duhem迟滞模型对压电陶瓷系统非线性建模。Duhem模型的基本表达式为:
式中:Ve为施加到压电堆(无压电效益)电容的电压; S为输出位移; α 为权重系数且α > 0; f(Ve)和g(Ve)为表达非线性的两个辅助函数。
根据Weierstrass第一逼近定理, 对Duhem模型中的连续函数f(Ve)和g(Ve), 在满足精度σ > 0条件下, 应用多项式函数进行逼近。设f(Ve)、g(Ve)阶次分别为n、m, 令f(Ve)=(Ve), (Ve)=(Ve), 其多项式分别为:
将式(3)代入式(2)得:
为了便于对参数进行辨识, 取m=5, n=5。
由文献[17]可知, 压电执行器电压降可以表示为:
Ve=Vp+
式中:Ve为输出电压; Vp为压电执行器上的电压降; Q为机电耦合系数; Cp为电容。
由机电耦合系数与压电材料的关系可得机电耦合系数的表达式为:
Q=
式中:A为压电堆有效面积; h为单层厚度; d(T)为电压系数。
同理可计算出压电堆整体的电容:
Cp=Nε T(8)
式中:N为压电执行器层数; ε T为介电系数。
根据文献[18]可得电压系数和温度之间的关系式:
d(T)=hd(T)
式中:Tref=20 ℃;
根据试验结果, 采用Matlab对方程(2)的参数α 、f(Ve)和g(Ve)进行辨识, 通过对参数的调整, 使试验结果和模拟结果实现良好的一致性。
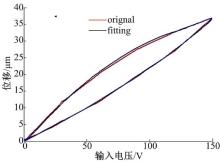
在25 ℃, 机械载荷为800 N时压电执行器仿真和试验结果如图7所示, 误差如图8所示。
由图7和图8可以看出, 模型的输出和试验数据基本吻合, 相对误差小于5%, 主要出现在最大输入电压的中间, 原因可能是由于迟滞方程的简化。
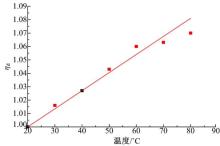
为了得到不同温度下的仿真结果, 根据所测试的不同温度下的试验结果, 对参数η d进行辨识。辨识结果如图9所示。η d通过对试验结果的拟合得到, 拟合值为:Kd=1.5× 10-3 ℃-1。
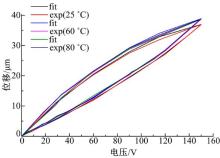
在相同的驱动电压下, 三个不同温度条件下的试验和仿真结果如图10所示。由图10可以看出, 不同温度下试验数据和仿真结果具有良好的一致性。为相似压电执行器的迟滞现象的控制和控制精度的提高奠定良好的基础。
(1)本文对应用于喷油器中的压电执行器准静态迟滞特性进行测量, 得到在不同预紧力、不同温度条件下的位移迟滞曲线。在预紧力为200~1200 N范围内, 压电执行器输出特性随着预紧力的增大呈现先增大后减小的趋势。压电执行器位移输出特性在800 N时达到最大值, 比200 N时的位移增加约4.3 μ m; 在温度为25~80 ℃范围内, 预紧力为定值时, 压电执行器位移输出特性随着温度的增加而增加。在温度从25 ℃增加到60 ℃时, 位移增加约为1.8 μ m, 从60 ℃增加到80 ℃时, 位移增加约为0.2 μ m。
(2) 一个包括压电堆迟滞特性和温度影响的数学模型被用来对试验结果进行模拟。在不同温度下试验数据和仿真结果具有较好的一致性。模型为执行器迟滞特性的控制提供了良好的基础。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|