引用本文
刘汉光, 王国强, 孟东阁, 赵寰宇. 液压挖掘机履带行走装置的合理预张紧力. 2018, 48(2): 486-491
LIU Han-guang, WANG Guo-qiang, MENG Dong-ge, ZHAO Huan-yu. Reasonable pre-tension research of crawler traveling gear of hydraulic excavator. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 486-491  
Doi:10.13229/j.cnki.jdxbgxb20161245
Permissions
Copyright©2018, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
液压挖掘机履带行走装置的合理预张紧力
刘汉光1,2, 王国强3, 孟东阁1, 赵寰宇3
1.江苏徐州工程机械研究院,江苏 徐州 221004
2.徐工集团高端工程机械智能制造国家重点实验室,江苏 徐州 221004
3.吉林大学 机械科学与工程学院,长春 130022

作者简介:刘汉光(1971-),男,高级工程师.研究方向:整机可靠性设计.E-mail:liuhangguang2@xcmg.com

基金项目:国家重点研发计划项目(2016YFC0802910); 国家科技支撑计划项目(2015BAF07B02)
摘要

针对液压挖掘机履带行走装置的合理预张紧力进行了分析研究。在多体动力学软件RecurDyn中建立了挖掘机的虚拟样机模型,并通过实验测得了在直行、原地转向以及差速转向3种工况下的履带行走装置张紧力的曲线,与仿真结果进行对比,验证了虚拟样机模型的准确。通过对直行、爬坡以及原地转向3种典型工况下的仿真分析,得到了在改变履带行走装置预张紧力情况下,履带行驶时张紧力的变化情况,通过张紧力曲线的标准差来判断其波动情况,进而得到合理的预张紧力与车重的比例系数。

关键词: 机械工程; 液压挖掘机; 虚拟样机仿真; 预张紧力
中图分类号:U469 文献标志码:A 文章编号:1671-5497(2018)02-0486-06
Reasonable pre-tension research of crawler traveling gear of hydraulic excavator
LIU Han-guang1,2, WANG Guo-qiang3, MENG Dong-ge1, ZHAO Huan-yu3
1.Jiangsu Xuzhou Construction Machinery Research Institute, Xuzhou 221004, China
2.Jiangsu Xuzhou State Key Laboratory of Intelligent Manufacturing of Advanced Construction Machinery, Xuzhou 221004, China
3.College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China
Abstract

The research focuses on the determination of reasonable pre-tension of crawler traveling gear of hydraulic excavator. The virtual prototype model of the excavator was established in the multi-body dynamics software RecurDyn. The pre-tension curves of the crawler traveling gear were obtained by experiments under three working conditions, horizontal straight, pivot steering and differential steering. Experiment results verified the accuracy of the virtual prototype model by comparing with the simulation results. By simulation analysis of three typical working conditions, horizontal straight, climbing, and pivot steering, the changes of the track tension during movement on wheel were obtained with the transformations of pre-tension of the crawler driving device. According to the judgment of the fluctuations based on the standard deviation of the tension curves, the reasonable proportional coefficient between the pre-tension and vehicle weight is received.

Key words: mechanical engineering; hydraulic excavator; virtual prototype model simulation; pre-tension
0 引 言

履带行走装置作为一种具有高通过性的行走装置, 在工程机械装备方面有着十分广泛的应用。履带张紧装置的预张紧力是履带行驶前通过推动导向轮对履带链进行张紧而设定的。履带在行驶过程中张紧装置受到的压力为张紧力。预张紧力对履带行走性能具有很大的影响, 预张紧力过大, 使履带刚性太大, 张紧装置起不到缓冲作用, 同时会造成履带行走机械的内摩擦力的增加, 从而造成发动机功率的损失以及加快履带的磨损速度; 预张紧力太小又会使履带松弛, 起不到张紧作用, 会造成履带脱链。因此, 合适的预张紧力对于履带行走装置运行性能有着很大的影响。此外, 预张紧力对履带运行时的张紧力也有着较大影响。

在高速履带车辆履带行走装置张紧力研究方面, Nakanishi等[1, 2]通过对履带车辆系统的平面动力学分析得到了二维接触力的动力学方程。Choi等[3, 4]在Nakanishi工作的基础上, 建立了三维的履带车辆系统动力学方程。此外, 所建立的履带张紧力的数学模型可以通过多体动力学工具进行仿真验证[5, 6]。在重型履带车辆行走装置张紧力研究方面, Zhou等[7]通过分析重型履带车辆的驱动轮与链节啮合, 得到了合适的履带张紧力。对于液压挖掘机履带行走装置而言, 既不需要高速履带的高机动性, 也不需要重型履带的巨大载重量, 因此, 需要合适的预张紧力来保证液压挖掘机履带行走装置行驶性能的稳定。

本文在多体动力学软件RecurDyn中建立了挖掘机的虚拟样机模型, 并通过在直行、原地转向以及差速转向3种工况下对履带行走装置的张紧力实测, 验证了虚拟样机模型的准确性。

1 虚拟样机模型

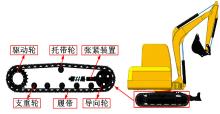
多体动力学软件RecurDyn中的Track(LM)模块, 可以将履带行走装置中驱动轮、导向轮、支重轮、托带轮以及履带板的三维模型导入, 将其定义为模块中系统可识别的相应部件, 然后进行履带链的装配, 快速创建完整的履带行走装置虚拟样机模型。图1为挖掘机整机虚拟样机模型, 其主要参数如表1所示。通过对挖掘机虚拟样机模型的仿真计算, 可以得到不同工况下履带预张紧力以及行驶过程中张紧力的仿真结果。

图1 挖掘机虚拟样机模型Fig.1 Virtual prototype model of excavator

表1 挖掘机模型主要参数 Table 1 Main parameters of excavator
2 实验验证

要从理论上验证挖掘机虚拟样机模型的准确性及可信度是非常困难的, 为了建立准确的虚拟样机模型, 需要通过实测挖掘机履带行走装置的关键性能指标, 为虚拟样机的准确提供数据基础。

2.1 测试仪器及方法

实验中使用DEWE SIRIUS数据采集器对测得的张紧力进行数据采集, 如图2所示。

图2 DEWE SIRIUS 数据采集器Fig.2 DEWE SIRIUS data acquisition system

由于张紧装置中的弹簧一端与履带架贴合, 此处的受力情况可以直接反映出张紧力的变化情况, 所以在张紧装置与履带架贴合端安装压力传感器, 将改装后的张紧装置安装于两侧履带行走装置上, 如图3所示。

将张紧装置上的压力传感器与数据采集器相连, 通过计算机对数据进行观测与存储。图4为挖掘机的实验样机, 主要由履带行走装置、上车、工作装置3个部分组成。对挖掘机实验样机在水平硬路面上行驶时的张紧力进行测量, 并与虚拟样机模型的动力学仿真结果进行对比验证。

图3 张紧力测量Fig.3 Measurement of tension

图4 挖掘机实验样机Fig.4 Experimental prototype of excavator

2.2 实验与虚拟样机仿真结果对比

对挖掘机虚拟样机模型在硬路面上进行直行、原地转向以及差速转向3种工况的仿真计算, 将得到的各工况下左、右两侧履带张紧力的结果与实验结果进行对比, 验证虚拟样机模型的准确。

2.2.1 直行工况

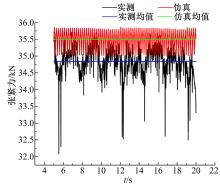
令挖掘机两侧履带均以2.30 km/h的速度行驶, 履带行走装置直行的张紧力实测与仿真曲线如图5所示, 实测均值为34 840.99 N, 仿真均值为35 497.75 N, 误差为1.89%, 吻合度较好。但实测张紧力曲线的波动比虚拟样机模型仿真得到的张紧力曲线的波动更大, 这是因为虚拟样机模型中建立的路面的平整度很高, 是理想的状态, 但实测时的路面平整度相对较低, 导致履带行驶过程中张紧装置受力不稳定, 会有较大的波动, 所以实测数据相比仿真结果波动更大。

图5 直行工况下张紧力曲线对比Fig.5 Comparison of tension curves in horizontal straight condition

2.2.2 原地转向工况

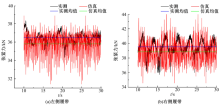
令挖掘机左侧履带以1.80 km/h的速度向前行驶, 右侧履带以1.80 km/h的速度向后行驶。履带行走装置原地转向工况下, 左侧履带的张紧力实测与仿真曲线如图6(a)所示, 实测均值为36 475.19 N, 仿真均值为35 800.79 N, 误差为1.85%, 吻合度较好。右侧履带的张紧力实测与仿真曲线如图6(b)所示, 实测均值为39 529.12 N, 仿真均值为38 844.48 N, 误差为1.73%, 吻合度较好。

图6 原地转向工况下张紧力曲线对比Fig.6 Comparison of tension curves in pivot steering condition

2.2.3 差速转向工况

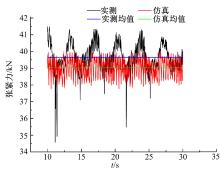
令挖掘机左侧履带以2.30 km/h的速度向前行驶, 右侧履带制动, 履带行走装置以0.75 m的半径实现差速转向。左侧履带张紧力实测与仿真曲线如图7所示, 实测均值为39 589.04 N, 仿真均值为38 678.49 N, 误差为2.30%, 吻合度较好。

图7 差速转向工况下张紧力曲线对比Fig.7 Comparison of tension curves in differential steering condition

3 仿真分析

履带行驶过程中履带张紧力的波动情况可以根据其标准差的数值大小来判断, 标准差的大小可以反映出张紧力波动的大小, 即履带行驶过程中履带链振动情况。而张紧力的变化受预张紧力取值的影响, 因此, 可以以张紧力的标准差作为预张紧力取值范围的依据。

3.1 直行工况

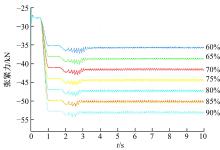
车辆以4.2 km/h的速度行驶, 预张紧力分别为整车质量G的60%、65%、70%、75%、80%、85%、90%。图8为7种预张紧力下履带行走装置张紧力曲线。

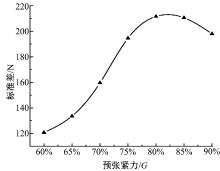
图9为7种预张紧力下车辆稳定行驶时张紧力标准差的变化曲线。由曲线可以看出, 在预张紧力为60%~70%车重区间时, 曲线呈加快上升的趋势增长; 在预张紧力为70%~75%车重区间时, 曲线趋近于线性增长; 在预张紧力为75%~80%车重区间时, 曲线呈减缓上升的趋势增长; 在预张紧力为大约82%车重时, 标准差达到最大值; 在预张紧力为82%~90%车重区间时曲线下降。

图8 直行工况下张紧力曲线Fig.8 Tension curves in horizontal straight condition

图9 直行工况下张紧力标准差曲线Fig.9 Standard deviation curves of tension in horizontal straight condition

3.2 爬坡工况

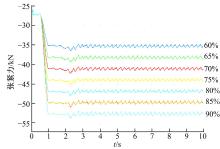
车辆以2.2 km/h的速度在坡度角为20° 的斜坡上行驶, 分别对60%、65%、70%、75%、80%、85%、90%车重的张紧力进行了仿真分析。图10为7种预张紧力下爬坡行驶张紧力曲线。

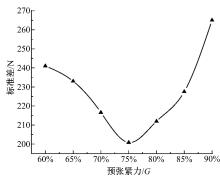
图10 爬坡工况下张紧力曲线Fig.10 Tension curves in climbing condition

图11为7种预张紧力下车辆稳定行驶时张紧力标准差的变化曲线。可以看出, 在预张紧力小于75%车重时, 稳定行驶时张紧力的标准差随着预张紧力的增大而减小, 在预张紧力为75%车重时标准差达到最小值; 在预张紧力大于75%车重时, 稳定行驶时张紧力的标准差随着预张紧力的增大而增大。以上结果表明, 在同一坡度角下, 75%车重的预张紧力情况下, 稳定行驶时张紧力的波动最小。

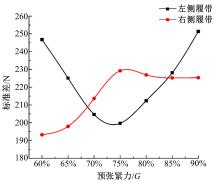
图11 爬坡工况下张紧力标准差曲线Fig.11 Standard deviation curves of tension in climbing condition

3.3 原地转向工况

左侧履带以0.4 km/h的速度前进, 右侧履带以0.4 km/h的速度后退, 实现向右的原地转向。左侧履带的张紧力小于右侧履带。图12(a) (b)分别为左侧履带和右侧履带在7种预张紧力下原地转向行驶张紧力的曲线。

图12 原地转向工况下张紧力曲线Fig.12 Tension curves in pivot steering condition

图13为7种预张紧力下, 车辆稳定行驶时左、右两侧履带张紧力标准差的变化曲线。可以看出, 原地转向稳定行驶时, 随着预张紧力的增大, 左侧(前进)履带张紧力的标准差在预张紧力小于75%车重时呈下降趋势, 在75%车重时达到最小; 在预张紧力大于75%车重时呈上升趋势。右侧(后退)履带张紧力的标准差在预张紧力小于75%车重时呈上升趋势, 在75%车重时达到最大; 在预张紧力大于75%车重时趋于平稳。

图13 原地转向工况下张紧力标准差曲线Fig.13 Standard deviation curves of tension in pivot steering condition

4 结束语

建立了挖掘机虚拟样机模型, 并通过在直行、原地转向以及差速转向3种工况下对履带行走装置的张紧力进行实测, 验证了虚拟样机模型的准确性。针对直行、爬坡以及原地转向3种典型工况, 在不同预张紧力下对履带行走装置张紧力的变化情况进行了仿真分析。在直行工况下, 预张紧力在70%~80%车重范围内更为合适; 在爬坡工况下, 预张紧力在70%~75%车重范围内更为合适; 在原地转向工况下, 预张紧力在75%~80%车重范围内更为合适。综合考虑以上3种典型工况, 较为合理的履带行走装置的预张紧力为整车重量的75%, 整车质量为5960 kg, 则预张紧力为43 806 N相对较为合理。

The authors have declared that no competing interests exist.

参考文献
[1] Nakanishi T, Shabana A A. Contact forces in the non-linear dynamic analysis of tracked vehicles[J]. International Journal for Numerical Methods in Engineering, 1994, 37(8): 1251-1275. [本文引用:1]
[2] Nakanishi T, Shabana A A. On the numerical solution of tracked vehicle dynamic equations[J]. Nonlinear Dynamics, 1994, 6(6): 391-417. [本文引用:1]
[3] Choi J H, Lee H C, ShabanaH A A. Spatial dynamics of multi-body tracked vehicles part I: spatial equations of motion[J]. Vehicle System Dynamics, 1998, 29(1): 27-49. [本文引用:1]
[4] Lee H C, Choi J H, ShabanaH A A. Spatial dynamics of multi-body tracked vehicles part II: contact forces and simulation results[J]. Vehicle System Dynamics, 1998, 29(2): 113-137. [本文引用:1]
[5] Huh K, Hong D. Tracktension estimation in tracked vehicles under various maneuvering tasks[J]. Journal of Dynamic Systems Measurement & Control, 2001, 123(2): 179-185. [本文引用:1]
[6] Matej J. Terrain-adaptive auxiliary track tensioning system for tracked vehicles[J]. Journal of Computational & Nonlinear Dynamics, 2013, 8(3): 689-698. [本文引用:1]
[7] Zhou M X, Ren Y P, Ye L, et al. Discussion oftrack tension for heavy tracked vehicles[J]. Advanced Materials Research, 2013, 813: 30-33. [本文引用:1]