压电双材料界面裂纹的强度因子分析

引用本文

孟广伟, 李荣佳, 王欣, 周立明, 顾帅. 压电双材料界面裂纹的强度因子分析. 2018, 48(2): 500-506
MENG Guang-wei, LI Rong-jia, WANG Xin, ZHOU Li-ming, GU Shuai. Analysis of intensity factors of interface crack in piezoelectric bimaterials. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 500-506 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170238
Permissions

压电双材料界面裂纹的强度因子分析

孟广伟, 李荣佳, 王欣, 周立明, 顾帅

吉林大学机械科学与工程学院,长春 130022

通信作者:周立明(1982-),男,副教授,博士. 研究方向:多物理场耦合断裂力学分析. E-mail:lmzhou@jlu.edu.cn

作者简介:孟广伟(1959-),男,教授,博士研究生. 研究方向:工程结构的断裂与疲劳. E-mail:mgw@jlu.edu.cn

基金项目:国家自然科学基金项目(11502092); 吉林省科技厅项目(20160520064JH,20170101043JC); 中央高校基本科研业务费专项项目(451170306066)

摘要

为满足实际工程中对求解压电双材料界面裂纹强度因子方法通用性和有效性的要求,基于压电界面断裂力学推导了压电双材料平面及反平面界面裂纹强度因子显示外推公式,通过力电耦合有限元模拟了裂纹尖端附近的位移场和电场,将裂纹尖端后面的裂纹张开位移和电势跃变代入强度因子显示外推公式,求解压电双材料的界面裂纹强度因子。以含中心裂纹压电双材料板为例,对不同载荷、单元数和加密形式下的强度因子进行了讨论,并与解析解作了对比。数值算例结果表明,本文方法具有计算简单、精度高等优点。

关键词: 信息处理技术; 力电耦合; 强度因子; 界面裂纹; 压电双材料

中图分类号:TB115 文献标志码:A 文章编号:1671-5497(2018)02-0500-07

Analysis of intensity factors of interface crack in piezoelectric bimaterials

MENG Guang-wei, LI Rong-jia, WANG Xin, ZHOU Li-ming, GU Shuai

College of Mechanical Science and Engineering,Jilin University,Changchun 130022,China

Abstract

In order to meet the requirement of commonality and effectiveness in solving the intensity factors of piezoelectric bimaterials with interface crack in practical engineering, based on piezoelectric interface facture mechanics, an explicit extrapolating formula of intensity factors for in-plane and anti-plane interface crack was derived. The interface crack-tip displacement field and electric filed of the piezoelectric bimaterials were simulated using the electromechanical coupling computation methods. Substituting the crack displacement and the electric potential jump at the back of the crack tip into the explicit extrapolating formula, the intensity factors of piezoelectric bimaterials with interface crack were solved. Considering a center interface crack in double piezoelectric plates, the intensity factors under different loadings, different numbers of elements, and different mesh refinement methods were discussed and compared with the analytical solution. Results of numerical examples show that the proposed method has the advantages of simple calculation and high accuracy.

Key words: information processing technology; electromechanical coupling; intensity factors; interfacial crack; piezoelectric biomaterials

Show Figures

0 引言

压电材料具有良好的力电耦合效应, 在智能材料和智能结构中发挥着重要的作用, 尤其在传感技术、驱动技术、超声技术和电子声学技术领域占有重要的地位。在实际工程中, 压电元件常以层状结构出现来提升其传感和驱动效果。压电材料所固有的脆性, 使其在制备及服役过程中易产生界面缺陷, 界面裂纹往往是该结构破坏的主要形式。近些年, 压电双材料界面裂纹的分析取得了一些成果。Govorukha等^[1]对压电材料的界面裂纹的研究进展进行了综述。Ou等^{[2, 3, 4]}提出了压电双材料在力电耦合作用下的界面裂纹奇异理论。Nishioka等^{[5, 6, 7]}给出了含界面裂纹压电双材料的J积分。Suo等^[8]推导了异相压电材料界面裂纹尖端处的裂纹张开位移和电势跃变与强度因子的隐式表达式。研究压电双材料的界面裂纹问题具有重要学术价值。

随着计算机硬件和软件的发展, 数值模拟方法成为求解压电双材料的断裂力学问题不可或缺的手段^[9]。Lei等^[10]基于边界元法研究了各向异性压电双材料在力电耦合冲击载荷作用下的动态强度因子。Ma等^[11]基于扩展有限元法计算了含裂纹压电双材料的J积分。Fang等^[12]采用无网格法对压电界面裂纹尖端处的应力场和电场进行了模拟。Zhao等^[13]基于Green函数和位移阶跃性对界面压电材料进行了研究。Gherrous等^[14]推导了反平面载荷作用下无限大板和半无限大板J积分公式。Sladek等^[15]基于无网格法对力载作用下的压电界面裂纹问题进行了分析。Loboda等^[16]研究了压电双材料接触区域界面裂纹问题。Feng等^[17]分析了压电双材料多界面裂纹问题。Choi等^[18]对压电双材料三共线反平面裂纹进行了研究。目前, 新型数值计算方法缺乏通用性^[19]。求解断裂参数的J积分求解较为复杂, 虚拟裂纹闭合法^[20]计算精度相对较低, 工程实际中需求简单有效的求解压电双材料界面裂纹强度因子方法。

本文基于广义直接位移法求解裂纹尖端附近的位移场和电场。推导了裂尖强度因子显示外推公式, 并从力电耦合有限元计算结果中提取相关数据代入压电双材料界面裂纹的位移外推法中, 求解了压电双材料界面裂纹的强度因子。

1 强度因子的显示外推公式

考虑广义平面压电双材料问题如图1所示,

	Figure Option View Download New Window
	图1 一个半无限压电双材料的界面裂纹Fig.1 An interface crack in a semi-infinite piezoelectric bimaterials

广义位移u(位移u_i和电势φ )和广义应力σ (应力σ _i₂和合力D₂), 其一般解可用四维Stroh形式^[15]:

u=2Re $[Af (z)]$ (1)

$[σ_{i 2}]$ =2Re $[{Bf}^{'} (z)]$ (2)

式中:

u= $\begin{matrix} {(u_{1}, u_{2}, u_{3}, φ)}^{T} \end{matrix}$ (3)

$[σ_{i 2}]$ = $\begin{matrix} {(σ_{12}, σ_{22}, σ_{32}, D_{2})}^{T} \end{matrix}$ (4)

f(z)为四阶复合势函数, 如下:

f(z)= $\begin{matrix} {(f_{1} (z_{1}), f_{2} (z_{2}), f_{3} (z_{3}), f_{4} (z_{4}))}^{T} \end{matrix}$ (5)

z_α=x₁+p_αx₂(6)

式中:p_α为式(7)特征方程中虚部大于零的特征值, 对应于p_α的特征向量为a_α $\begin{matrix} (α = 1, 2, 3, 4) \end{matrix}$ 。

$\begin{matrix} [Q + p (R + R^{T}) + p^{2} T] \end{matrix}$ a=0(7)

式中:

Q= $\begin{matrix} [\begin{matrix} c_{i 1 k 1} & e_{1 i 1} \\ {e^{T}}_{1 k 1} & - g_{11} \end{matrix}] \end{matrix}$ (8)

R= $\begin{matrix} [\begin{matrix} c_{i 1 k 2} & e_{2 i 1} \\ {e^{T}}_{1 k 2} & - g_{12} \end{matrix}] \end{matrix}$ (9)

T= $\begin{matrix} [\begin{matrix} c_{i 2 k 2} & e_{2 i 2} \\ {e^{T}}_{2 k 2} & - g_{22} \end{matrix}] \end{matrix}$ (10)

式中:c_ijkl为弹性常数; e_kij为压电常数; g_ik为介电常数。

矩阵A和B由式(7)的特征向量组成:

A= $\begin{matrix} (a_{1}, a_{2}, a_{3}, a_{4}) \end{matrix}$ (11)

B= $\begin{matrix} (b_{1}, b_{2}, b_{3}, b_{4}) \end{matrix}$ (12)

$\begin{matrix} \begin{matrix} b_{α} = (R^{T} + p_{α} T) a_{α} = - (1 / p_{α}) (Q + p_{α} R) a_{α} \end{matrix} \end{matrix}$ (13)

对于不可渗透双压电材料界面时, Hermitian矩阵Y和H为:

Y=iAB^-¹(14)

H=Y⁽¹⁾+ $\begin{matrix} {\bar{Y}}^{(2)} \end{matrix}$ (15)

式中:上标(1)和(2)代表材料1和材料2。

裂纹尖端场的奇异性归结为以下特征值问题:

ω =e^2π^γHω (16)

式中:ω 为Hermitian矩阵特征值问题所对应的特征的量。

把矩阵H拆分成一个实部D和一个虚部W, 如下:

H=D+iW(17)

由式(16)得:

‖ D^-¹W+iβ I‖ =β ⁴+2bβ ²+c=0(18)

式中:

γ =-arctanβ (19)

b=tr $\begin{matrix} [{(D^{- 1} W)}^{2}] \end{matrix}$ (20)

c=‖ D^-¹W‖ (21)

式中:β 为式(18)的根; γ 对应的值± ε 、± iκ 互为共轭对; “ tr” 为矩阵的迹。

由于W为偶次的反对称矩阵≥ 0, 又由于< 0, 所以c≤ 0, 因此γ ≥ 0。振荡参数ε 和κ 为:

ε =cot $\begin{matrix} {[{(b^{2} - c)}^{\frac{1}{2}} - b]}^{\frac{1}{2}} \end{matrix}$ (22)

κ =cot $\begin{matrix} {[{(b^{2} - c)}^{\frac{1}{2}} + b]}^{\frac{1}{2}} \end{matrix}$ (23)

该问题广义位移差δ _i(i=1, 2, 3, 4)与强度因子K_i(i=1, 2, 3, 4)的关系为:

$\begin{matrix} {[δ_{1} δ_{2} δ_{3} δ_{4}]}^{T} \end{matrix}$ =4 $\begin{matrix} \sqrt[]{\frac{r}{2 π}} \end{matrix}$ HS $\begin{matrix} {(I + {\bar{H}}^{- 1} H)}^{- 1} \end{matrix}$ · $\begin{matrix} {[\begin{matrix} K_{2} & K_{1} & K_{3} & K_{4} \end{matrix}]}^{T} \end{matrix}$ (24)

式中:K₁为Ⅰ 型裂纹的应力强度因子; K₂为Ⅱ 型裂纹的应力强度因子; K₃为Ⅲ 型裂纹的应力强度因子; K₄为电位移强度因子。

S=ω diag· $\begin{matrix} [r^{iε} \frac{coshπε}{1 + 2 iε} r^{- iε} \frac{coshπε}{1 - 2 iε} r^{κ} \frac{coshπκ}{1 + 2 κ} r^{- κ} \frac{coshπκ}{1 - 2 κ}] \end{matrix}$ ω ^-¹(25)

式中:r为距裂尖距离。

对式(24)中的平面和反平面裂纹问题进行分析。对于平面界面裂纹问题, 距裂纹尖端r处的张开位移和电势跃变为:

$\begin{matrix} {[δ_{1} δ_{2} δ_{4}]}^{T} \end{matrix}$ = $\begin{matrix} \frac{4 \sqrt[]{r}}{\sqrt[]{2 π}} \end{matrix}$ Hω diag $\begin{matrix} [ζ_{1} ζ_{2} 1] \end{matrix}$ ω ^-¹· $\begin{matrix} {(I + {\bar{H}}^{- 1} H)}^{- 1} \end{matrix} \begin{matrix} {[K_{2} K_{1} K_{4}]}^{T} \end{matrix}$ (26)

式中:当b≤ 0时, ζ ₁=rⁱ^ε $\begin{matrix} \frac{coshπε}{1 + 2 iε} \end{matrix}$ , ζ ₂=r^-ⁱ^ε $\begin{matrix} \frac{coshπε}{1 - 2 iε} \end{matrix}$ ; b> 0时, ζ ₁=r^κ $\begin{matrix} \frac{coshπκ}{1 + 2 κ} \end{matrix}$ , ζ ₂=r^-κ $\begin{matrix} \frac{coshπκ}{1 - 2 κ} \end{matrix}$ 。ω diag $\begin{matrix} [ζ_{1} ζ_{2} 1] \end{matrix}$ ω ^-¹项为I、E和E²的线性组合, 相应的矩阵为:

T₁=2H $\begin{matrix} {(I + {\bar{H}}^{- 1} H)}^{- 1} \end{matrix}$ (27)

T₂=2HE $\begin{matrix} {(I + {\bar{H}}^{- 1} H)}^{- 1} \end{matrix}$ (28)

T₃=2HE² $\begin{matrix} {(I + {\bar{H}}^{- 1} H)}^{- 1} \end{matrix}$ (29)

式中:I为单位矩阵; E=WD^-¹。

整理式(26), 得到裂纹尖端强度因子显示外推公式:

$\begin{matrix} {[K_{2} K_{1} K_{4}]}^{T} \end{matrix}$ =M $\begin{matrix} {[δ_{1} δ_{2} δ_{4}]}^{T} \end{matrix}$ (30)

式中:

M= $\begin{matrix} {[(1 - \frac{ζ_{1} + ζ_{2}}{2}) \frac{T_{3}}{β^{2}} + \frac{i (ζ_{1} - ζ_{2})}{2 β} T_{2} + T_{1}]}^{- 1} \end{matrix}$ (31)

对于反平面界面裂纹问题, 位移场和电势场仍然保持平方根奇异性, 有

$\begin{matrix} \{\begin{matrix} A = [\begin{matrix} 0 & 1 \\ 1 & e_{15} / g_{11} \end{matrix}] \\ B = i [\begin{matrix} e_{15} & c_{44} + e_{15}^{2} / g_{11} \\ - g_{11} & 0 \end{matrix}] \end{matrix} \end{matrix}$ (32)

Y=iAB^-¹= $\begin{matrix} \frac{1}{c_{44} g_{11} + e_{15}^{2}} \end{matrix} \begin{matrix} [\begin{matrix} g_{11} & e_{15} \\ e_{15} & - c_{44} \end{matrix}] \end{matrix}$ (33)

式中:c₄₄、e₁₅和g₁₁分别为弹性矩阵系数、压电矩阵系数和介电矩阵系数。

式(15)可改写为:

H=Y⁽¹⁾+ $\begin{matrix} {\bar{Y}}^{(2)} \end{matrix}$ =Y⁽¹⁾+Y⁽²⁾= $\begin{matrix} [\begin{matrix} H_{11} H_{12} \\ H_{21} H_{22} \end{matrix}] \end{matrix}$ (34)

H₁₁= $\begin{matrix} \overset{2}{\sum_{i = 1}} \end{matrix} \begin{matrix} \frac{g_{11}^{(i)}}{c_{44}^{(i)} g_{11}^{(i)} + e_{15}^{(i)} e_{15}^{(i)}} \end{matrix}$ (35)

H₁₂=H₂₁= $\begin{matrix} \overset{2}{\sum_{i = 1}} \end{matrix} \begin{matrix} \frac{e_{15}^{(i)}}{c_{44}^{(i)} g_{11}^{(i)} + e_{15}^{(i)} e_{15}^{(i)}} \end{matrix}$ (36)

H₂₂= $\begin{matrix} \overset{2}{\sum_{i = 1}} \end{matrix} \begin{matrix} \frac{- c_{44}^{(i)}}{c_{44}^{(i)} g_{11}^{(i)} + e_{15}^{(i)} e_{15}^{(i)}} \end{matrix}$ (37)

式中:(i)为材料i的材料参数。

整理式(24), 得到反平面裂纹裂尖强度因子显示外推公式:

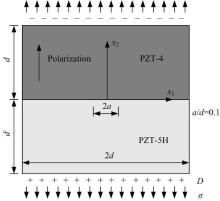
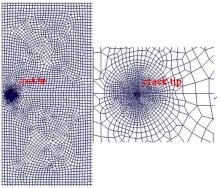
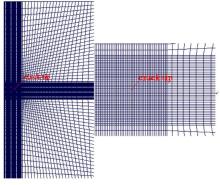
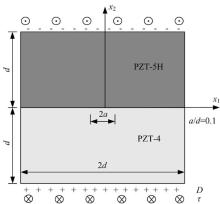
$\begin{matrix} {[K_{3} K_{4}]}^{T} \end{matrix}$ =H^-¹ $\begin{matrix} {[δ_{3} δ_{4}]}^{T} \end{matrix}$ (38)

2 平面界面裂纹问题

由PZT-4和PZT-5H组成的中心裂纹为2a的双压电材料, 材料参数如表1所示。受σ =1.0 MPa的拉应力和D=0.001 C/m²的电位移, 极化方向为x₂方向, 几何尺寸为2d=40 mm× 40 mm, 中心裂纹长度2a=4 mm, 如图2所示。由于载荷和结构的对称性, 取模型的一半计算, ABAQUS采用CPS8E单元, 裂尖处采用图3~图5所示的开裂前3种单元划分模式(Ⅰ :圆形加密、Ⅱ :均匀加密和Ⅲ :矩形加密)。

表2给出了不同载荷及网格加密时距裂纹尖端0.02a处的裂纹张开位移和电势跃变, 由显示外推公式(30)得到其强度因子。表3给出了3种网格加密形式时力场单独作用下强度因子计算结果与解析解, 并给出了误差。表4给出了3种网格加密形式时电场单独作用下强度因子计算结果与解析解。表5给出了3种网格加密形式时力电耦合作用下强度因子计算结果与解析解, 并给出了误差。可见, 3种计算模型下均得到了精度较高的强度因子, 与解析解比较, 最大误差仅为3.9%, 采用圆形加密方式下的强度因子计算精度最高。

表1 材料常数 Table 1 Material constants

	Figure Option View Download New Window
	图2 双压电材料中心界面裂纹Fig.2 Interfacial center crack in piezoelectric bimaterials

	Figure Option View Download New Window
	图3 裂尖圆形加密(Elements:4026)Fig.3 Round refinement at crack tip (Elements:4026)

	Figure Option View Download New Window
	图4 裂尖均匀加密(Elements:5418)Fig.4 Uniform refinement at crack tip (Elements:5418)

	Figure Option View Download New Window
	图5 裂尖矩形加密(Elements:6987)Fig.5 Rectangular refinement at crack tip (Elements:6987)

表2 不同载荷及网格加密时裂纹张开位移与电势跃变 Table 2 Crack opening displacement and electric potential jump by different loadings and mesh refinement methods

表3 在力载荷作用时不同网格加密下强度因子 Table 3 Intensity factors by different mesh refinement methods under mechanical loading

表4 在电载荷作用时不同网格加密下强度因子 Table 4 Intensity factors by different mesh refinement methods under electric loading

表5 在力电载荷作用时不同网格加密下强度因子 Table 5 Intensity factors by different mesh refinement methods under electromechanical loading

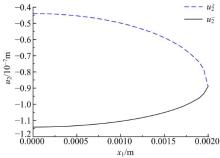
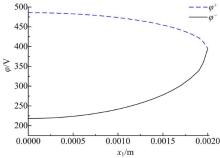
图6和图7分别给出了电载荷作用时圆形加密方式下裂纹线上节点位移值和电势值, 提取裂纹尖端后面0.02a~0.6a范围附近裂纹张开位移及电势跃变可以得到稳定收敛的强度因子。对于裂纹尖端网格加密方式, 在CPU:Inter(R) Core(TM) i5-3470 3.20 GHz, RAM:8GB情况下, 力电载荷作用时, 圆形加密耗时1.7 s, 均匀加密耗时2.2 s, 矩形加密耗时2.9 s。裂尖采用圆形加密方式计算强度因子具有方法便捷、精度高、耗时少等优点。

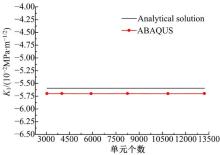
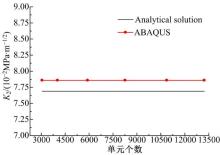
图8~图10分别给出了力电载荷作用下, 加密区域内单元类型和数量不变, 采用圆形网格加密时单元个数(3058、4026、5907、8256、10866和13217)与强度因子的关系图。可见, 强度因子受加密区域以外的单元影响比较小, 主要受加密区域内单元的加密形式的影响。

	Figure Option View Download New Window
	图6 电载荷作用时裂纹张开位移Fig.6 Crack opening displacement under electric loading

	Figure Option View Download New Window
	图7 电载荷作用时电势跃变Fig.7 Electric potential jump under electric loading

	Figure Option View Download New Window
	图8 强度因子K₁与单元个数的关系Fig.8 Relationship between intensity factor K₁ and number of elements

	Figure Option View Download New Window
	图9 强度因子K₂与单元个数的关系Fig.9 Relationship between intensity factor K₂ and number of elements

	Figure Option View Download New Window
	图10 强度因子K₄与单元个数的关系Fig.10 Relationship between intensity factor K₄ and number of elements

3 反平面界面裂纹问题

如图11所示, 无限大压电双材料中有一中心长为2a=10 mm的穿透裂纹, 材料参数由PZT-5H和PZT-4组成。在边界受远场载荷τ =5.94 MPa和D=0.003 C/m², x₁轴沿界面方向, x₃轴为压电材料的极化方向。

	Figure Option View Download New Window
	图11 压电双材料反平面界面裂纹Fig.11 Anti-plane interface crack in piezoelectric bimaterials

表6给出了力电载荷作用时反平面界面强度因子计算结果与解析解, 并给出了误差。与解析解比较, 最大误差仅4.8%。可见, 本文方法具有方法便捷、精度高等优点。

表6 在力电载荷作用时反平面界面强度因子 Table 6 Anti-plane interface intensity factors under electromechanical loading

4 结论

(1)基于强度因子显示外推公式, 通过提取相应裂纹张开位移和电势跃变计算强度因子具有方法便捷、精度高等优点。

(2)当裂尖处采用圆形区域加密时, 求解精度最高, 效率最高。

(3)强度因子受加密区域以外的单元影响比较小, 主要受加密区域内单元加密形式的影响。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Govorukha V, Kamlah M, Loboda V, et al. Interface cracks in piezoelectric materials[J]. Smart Materials and Structures, 2016, 25(2): 323-335. [本文引用:1]
[2]	Ou Z C. Singularity parameters ε and κ for interface cracks in transversely isotropic piezoelectricbimaterials[J]. International Journal of Fracture, 2003, 119(2): 41-46. [本文引用:1]
[3]	Ou Z C, Chen Y H. Near-tip stress fields and intensity factors for an interface crack in metal/piezoelectric bimaterials[J]. International Journal of Engineering Science, 2004, 42(13): 1407-1438. [本文引用:1]
[4]	Ou Z C, Chen Y H. Interface crack-tip generalized stress field and stress intensity factors in transversely isotropic piezoelectric bimaterials[J]. Mechanics Research Communications, 2004, 31(4): 421-428. [本文引用:1]
[5]	Nishioka T, Shen S, Yu J. Dynamic J integral, separated dynamic J integral and component separation method for dynamic interfacial cracks in piezoelectric bimaterials[J]. International Journal of Fracture, 2003, 122(3/4): 101-130. [本文引用:1]
[6]	Hu S, Shen S, Nishioka T. Numerical analysis for a crack in piezoelectric material under impact[J]. International Journal of Solids and Structures, 2007, 44(25): 8457-8492. [本文引用:1]
[7]	Shen S, Nishioka T, Kuang Z B. Impact interfacial fracture for piezoelectric ceramic[J]. Mechanics Research Communications, 1999, 26(3): 347-352. [本文引用:1]
[8]	Suo Z, Kuo C M, Barnett D M, et al. Fracture mechanics for piezoelectric ceramics[J]. Journal of the Mechanics and Physics of Solids, 1992, 40(4): 739-765. [本文引用:1]
[9]	Zhou L M, Meng G W, Li F, et al. A cell-based smoothed XFEM for fracture in piezoelectric materials[J]. Advances in Materials Science and Engineering, 2016, 2016(5): 1-14. [本文引用:1]
[10]	Lei J, Zhang C. Time-domain BEM for transient interfacial crack problems in anisotropic piezoelectric bimaterials[J]. International Journal of Fracture, 2012, 174(2): 163-175. [本文引用:1]
[11]	Ma P, Su R K L, Feng W J, et al. The extended finite element method with new crack-tip enrichment functions for an interface crack between two dissimilar piezoelectric materials[J]. International Journal for Numerical Methods in Engineering, 2015, 103(2): 94-113. [本文引用:1]
[12]	Fang D, Li F, Liu B, et al. Advances in developing electromechanically coupled computational methods for piezoelectrics/ferroelectrics at multiscale[J]. Applied Mechanics Reviews, 2013, 65(6): 060802. [本文引用:1]
[13]	Zhao Y F, Zhao M H, Pan E, et al. Analysis of an interfacial crack in a piezoelectric bi-material via the extended Green's functions and displacement discontinuity method[J]. International Journal of Solids and Structures, 2014, 51(6): 1456-1463. [本文引用:1]
[14]	Gherrous M, Ferdjani H. Analysis of a Griffith crack at the interface of two piezoelectric materials under anti-plane loading[J]. Continuum Mechanics and Thermodynamics, 2016, 28(6): 1683-1704. [本文引用:1]
[15]	Sladek J, Sladek V, Wünsche M, et al. Analysis of an interface crack between two dissimilar piezoelectric solids[J]. Engineering Fracture Mechanics, 2012, 89: 114-127. [本文引用:2]
[16]	Loboda V, Sheveleva A, Lapusta Y. An electrically conducting interface crack with a contact zone in a piezoelectric bimaterial[J]. International Journal of Solids and Structures, 2014, 51(1): 63-73. [本文引用:1]
[17]	Feng F X, Lee K Y, Li Y D. Multiple cracks on the interface between a piezoelectric layer and an orthotropic substrate[J]. Acta Mechanica, 2011, 221(3/4): 297-308. [本文引用:1]
[18]	Choi S R, Chung I. Analysis of three collinearantiplane interfacial cracks in dissimilar piezoelectric materials under non-self equilibrated electromechanical loadings on a center crack[J]. Journal of Mechanical Science and Technology, 2013, 27(10): 3097-3101. [本文引用:1]
[19]	孟广伟, 赵云亮, 李锋, 等. 含多裂纹结构的断裂可靠性分析[J]. 吉林大学学报: 工学版, 2008, 38(3): 614-618. Meng Guang-wei, Zhao Yun-liang, Li Feng, et al. Reliability analysis of structures with multi-crack[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(3): 614-618. [本文引用:1]
[20]	彭惠芬, 孟广伟, 周立明, 等. 基于小波有限元法的虚拟裂纹闭合法[J]. 吉林大学学报: 工学版, 2011, 41(5): 1364-1368. Peng Hui-fen, Meng Guang-wei, Zhou Li-ming, et al. Virtual crack closure technique based on wavelet finite element method[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(5): 1364-1368. [本文引用:1]

2016

0.0

... Govorukha等^[1]对压电材料的界面裂纹的研究进展进行了综述 ...

2003

0.0

... Ou等^[2,3,4]提出了压电双材料在力电耦合作用下的界面裂纹奇异理论 ...

2004

0.0

... Ou等^[2,3,4]提出了压电双材料在力电耦合作用下的界面裂纹奇异理论 ...

2004

0.0

... Ou等^[2,3,4]提出了压电双材料在力电耦合作用下的界面裂纹奇异理论 ...

2003

0.0

... Nishioka等^[5,6,7]给出了含界面裂纹压电双材料的J积分 ...

2007

0.0

... Nishioka等^[5,6,7]给出了含界面裂纹压电双材料的J积分 ...

1999

0.0

... Nishioka等^[5,6,7]给出了含界面裂纹压电双材料的J积分 ...

1992

0.0

... Suo等^[8]推导了异相压电材料界面裂纹尖端处的裂纹张开位移和电势跃变与强度因子的隐式表达式 ...

2016

0.0

... 随着计算机硬件和软件的发展,数值模拟方法成为求解压电双材料的断裂力学问题不可或缺的手段^[9] ...

2012

0.0

... Lei等^[10]基于边界元法研究了各向异性压电双材料在力电耦合冲击载荷作用下的动态强度因子 ...

2015

0.0

... Ma等^[11]基于扩展有限元法计算了含裂纹压电双材料的J积分 ...

2013

0.0

... Fang等^[12]采用无网格法对压电界面裂纹尖端处的应力场和电场进行了模拟 ...

2014

0.0

... Zhao等^[13]基于Green函数和位移阶跃性对界面压电材料进行了研究 ...

2016

0.0

... Gherrous等^[14]推导了反平面载荷作用下无限大板和半无限大板J积分公式 ...

2012

0.0

... Sladek等^[15]基于无网格法对力载作用下的压电界面裂纹问题进行了分析 ...

... _i₂和合力D₂),其一般解可用四维Stroh形式^[15]: ...

2014

0.0

... Loboda等^[16]研究了压电双材料接触区域界面裂纹问题 ...

2011

0.0

... Feng等^[17]分析了压电双材料多界面裂纹问题 ...

2013

0.0

... Choi等^[18]对压电双材料三共线反平面裂纹进行了研究 ...

2008

0.0

. 2008, 38(3):614-618

Reliability analysis of structures with multi-crack

Meng Guang-wei , Zhao Yun-liang , Li Feng

College of Mechanical Science and Engineering, Jilin University, Changchun 130022,China

Based on stochastic finite element method and reliability theory, a reliability analysis model for structures with multicrack was presented. Firstly, the expression of stress intensity factors was proposed using the least squares method. Secondly, uncertainties in material parameters, crack length and loading which affect fracture of structures were described as random variables, the reliability index for each crack was obtained by first order reliability method and stochastic finite element method. Finally, the structure with multicracks was taken as a series system composed of all cracks, and the correlation coefficients between failure models were evaluated. The failure probability of the structure was computed by Ditlevsen bounds method. A numerical example was performed for a finite plate with multiple holes and cracks. The result shows that the suggested method is feasible and applicable.

基于随机有限元法和可靠性设计理论，建立了一种含多裂纹结构的断裂可靠性分析模型。首先，根据最小二乘法则建立应力强度因子的表达式，然后将影响结构断裂的不确定因素视为随机变量，通过一阶二次矩法和随机有限元法求出每条裂纹的可靠度指标，最后将含多裂纹结构看作一个由所有裂纹组成的串联系统，求出各裂纹之间的相关系数，并得出多裂纹结构失效概率的Ditlevsen界限值。数值算例表明，本方法具有较强的适用性。

... 目前,新型数值计算方法缺乏通用性^[19] ...

2011

0.0

. 2011, 41(5):1364-1368

Virtual crack closure technique based on wavelet finite element method

基于小波有限元法的虚拟裂纹闭合法

Peng Hui-fen , Meng Guang-wei , Zhou Li-ming

彭惠芬, 孟广伟, 周立明

... 求解断裂参数的J积分求解较为复杂,虚拟裂纹闭合法^[20]计算精度相对较低,工程实际中需求简单有效的求解压电双材料界面裂纹强度因子方法 ...