引用本文
王扬, 吕凤妍, 徐天月, 于建群. 大豆籽粒形状和尺寸分析及其建模. 2018, 48(2): 507-517
WANG Yang, LYU Feng-yan, XU Tian-yue, YU Jian-qun. Shape and size analysis of soybean kernel and modeling. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 507-517  
Doi:10.13229/j.cnki.jdxbgxb20170953
Permissions
Copyright©2018, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
大豆籽粒形状和尺寸分析及其建模
王扬, 吕凤妍, 徐天月, 于建群
吉林大学 生物与农业工程学院,长春 130022
通信作者:于建群(1958-),男,教授,博士生导师. 研究方向:农业机械的数字化设计. E-mail:yujianqun@jlu.edu.cn

作者简介:王扬(1987-),男,博士研究生. 研究方向:农业机械的数字化设计. E-mail:yangwl2@mails.jlu.edu.cn

基金项目:国家自然科学基金项目(51675218)
摘要

为建立大豆籽粒的离散元法分析模型,对大豆籽粒的几何形状和尺寸参数进行了测试分析。由测试分析可知,大豆籽粒的几何形状与椭球近似,三轴尺寸均服从正态分布,三轴尺寸中主尺寸与次尺寸间存在一定的函数关系。在此基础上,提出一种基于球充填的大豆籽粒建模方法,即将大豆籽粒的几何形状简化成椭球形,以实际大豆籽粒的各三轴尺寸平均值作为椭球的三轴尺寸,采用球充填方法建立椭球(单个籽粒)的分析模型;选单个籽粒分析模型的主尺寸,按正态分布随机生成,次尺寸通过与主尺寸的关系计算得出,由此建立具有不同尺寸及分布的大豆籽粒群体模型。以2个品种大豆籽粒为例,通过堆积试验和本文提出的“自流筛分”试验的仿真与试验结果对比可知,当充填球数为5时,仿真结果与试验结果较接近,初步证明了本文提出的大豆籽粒建模方法的可行性和有效性。

关键词: 农业工程; 离散元法; 大豆籽粒; 颗粒建模; 仿真分析
中图分类号:S126 文献标志码:A 文章编号:1671-5497(2018)02-0507-11
Shape and size analysis of soybean kernel and modeling
WANG Yang, LYU Feng-yan, XU Tian-yue, YU Jian-qun
College of Biological and Agricultural Engineering, Jilin University, Changchun 130022, China
Abstract

In order to build the analytic model of soybean kernel using Discrete Element Method (DEM), the shape and size of soybean kernel are measured and analyzed. It is found that the shape of a soybean kernel can be approximated to an ellipsoid. The three axis dimensions follow normal distribution, and there exists a certain correlation between the primary dimension and the secondary dimension. On this basis, a soybean kernel modeling method is proposed based on the sphere filling. The shape of the soybean kernel is approximated to an ellipsoid, and the three axis dimensions are determined as the mean values of measured soybean kernels. The primary dimension of the analytical model of a kernel, which follows normal distribution, is randomly generated, and the secondary dimension of the kernel is calculated according to the relationship between the primary and secondary dimensions. As a result, the assemble model of the soybean kernels with different size and distribution is built. Two varieties of soybean kernels are selected as the research objects. By comparison between the simulated results and the experimental results of the packing test and the self-flowing screening test proposed in this work, it is shown that, when the amount of filling-spheres is five, the simulation results are in good agreement with the experiment results, thus, preliminarily verifying the effectiveness and feasibility of proposed modeling method.

Key words: agricultural engineering; discrete element method; soybean kernel; particle modelling; simulation analysis
0 引 言

大豆作为重要的豆类作物, 其在收获、脱粒、分离清选、输送、加工和包装等过程中始终存在籽粒与机械部件的接触作用。在采用离散元法[1, 2]分析这些接触作用并优化设计机械部件时, 需要建立较精确的大豆籽粒分析模型。目前, 在建立大豆籽粒分析模型时, 国内外学者大多将大豆籽粒简化成椭球形[3, 4, 5, 6]。但大豆籽粒的几何形状与椭球近似程度如何, 还鲜见研究报道。此外, 在大豆籽粒群体中, 各个籽粒的尺寸均不同, 如何建立大豆籽粒群体的模型, 使群体中颗粒的尺寸分布与实际大豆籽粒的尺寸分布相一致, 也需要深入研究。

目前, 建立大豆籽粒分析模型均采用球充填方法。如Lu[7]和Vu-Quoc等[3] 分别采用1个球和4个球充填来建立大豆籽粒的分析模型。Boac等[4]采用1~4个球充填建立大豆籽粒的分析模型, 还通过分析得出1个球充填较好的结论。Tao等[5]通过仿真与试验对比得出3球充填模型较好。可以说不同球数的充填模型, 具有不同的特点, 但对于三轴尺寸不等的大豆籽粒, 采用几个球充填建模更适合, 目前还无结论。此外, 测量大豆籽粒模型的精度目前多采用颗粒的堆积角[8]、颗粒的容积密度[4]和颗粒的流型[5]等方法, 并将仿真结果与试验结果进行对比验证。然而, 这些验证方法反映的是颗粒群体效果, 而不能直接反映单个颗粒形状及尺寸的影响。因此, 目前采用的验证方法还不充分。为此, 本文提出“ 自流筛分” 的验证方法。

本文以4个品种大豆籽粒为研究对象, 对大豆籽粒的几何形状和尺寸进行测试分析, 在此基础上, 提出一种基于球充填的单个大豆籽粒和群体籽粒的建模方法; 通过堆积试验和本文提出的“ 自流筛分” 试验的仿真结果与试验结果的对比, 初步验证本文提出的大豆籽粒建模方法的可行性和有效性, 可为相关研究提供参考。

1 大豆籽粒形状的测试分析

为具有代表性, 本文以沂蒙山小黄豆、沂蒙山笨大豆、四川农家豆和黑龙江大豆, 这4个品种的大豆籽粒为研究对象(以下分别简称为沂小豆、沂笨豆、川豆和黑豆)。在这4个品种大豆籽粒中, 随机挑选外形完好的大豆籽粒各3粒。利用精度为0.05 mm的三维扫描仪获得大豆籽粒外轮廓的点云数据, 同时, 将点云数据与三轴尺寸相同的椭球进行比较, 如图1所示。

图1 单个大豆籽粒形状与三轴尺寸相同的椭球形状比较Fig.1 Comparison between the shape of a single soybean kernel and that of an ellipsoid with the same sizes

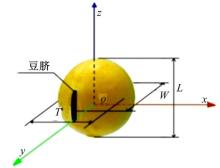
为了获得精确的比较数值, 建立图2所示的直角坐标系。在该坐标系中, 将坐标平面xoz绕x轴以22.5° 为转角进行旋转, 得到6个除xoz和xoy平面外的截面。同样, 将xoy和yoz坐标平面分别绕y轴和z轴旋转, 得到12个截面, 合计18个截面, 加上3个坐标平面, 共计得到21个截面。分别用这21个截面截取大豆籽粒的扫描轮廓图(见图1(b))和相同尺寸的椭球轮廓图(见图1(c)), 在这21个截面的每个截面上, 得到扫描轮廓与椭球轮廓间径向的最大差值, 如图3所示。

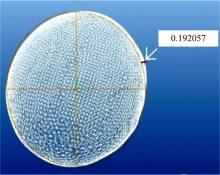图2 大豆籽粒三轴尺寸及坐标系Fig.2 Tri-axial dimensions of soybean kernel and its coordinate system

图3 大豆籽粒扫描轮廓与椭球轮廓间径向最大差值示意图Fig.3 Schematic diagram of maximal radial distance between contour of scanning image and that of ellipsoid

每个籽粒在21个截面上径向最大差值的平均值和标准差见表1。由表1可知, 每个大豆籽粒在21个截面上径向最大差值较小且小于0.5 mm, 因此在一定误差范围内, 可认为大豆籽粒形状近似为椭球, 即建模时可将大豆籽粒几何形状简化成椭球形。

表1 大豆籽粒形状与相同尺寸椭球轮廓线性尺寸差值比较 Table 1 Maximal radial distances on 21 cross sections for each soybean kernel of four varieties
2 大豆籽粒三轴尺寸的测试分析

对于单个大豆籽粒来说, 其三轴尺寸分别为长度(L)、宽度(W)、厚度(T), 如图2所示。以沂小豆和黑豆2个品种为例, 分别从中随机选取100粒, 用精度为0.01 mm的数显卡尺测量其三轴尺寸。

由测量结果可知, 大豆籽粒的三轴尺寸均近似服从正态分布。以黑豆籽粒为例, 其三轴尺寸的正态分布如图4所示。

图4 黑豆籽粒三轴尺寸的分布图Fig.4 Distributions of tri-axial dimensions of Heidou kernels

对2个品种大豆籽粒的三轴尺寸进行分析, 以黑豆籽粒为例, 如图5所示。可知, 大豆籽粒长-宽和宽-厚之间线性相关性明显大于长-厚之间的线性相关性。因此, 可定义宽度为主尺寸, 长度和厚度为次尺寸。次尺寸与主尺寸的关系式见表2。

取上述100粒沂小豆和黑豆籽粒的宽度作为主尺寸, 利用表2中的关系式, 分别计算出每粒大豆籽粒的长度(L')和厚度(T'), 与大豆籽粒实际的长度(L)和厚度(T)进行比较, 见表3。由表3可知, 长度和厚度的计算值与实际值相差较小。因此, 在建立大豆籽粒群体模型时, 可选择宽度为主尺寸, 按正态分布随机生成, 其他尺寸可根据与主尺寸的关系计算得出, 这样生成的籽粒群体尺寸及分布能比较接近于实际情况。

图5 黑豆籽粒三轴尺寸间关系的散点图Fig.5 Scatter diagrams of relations between tri-axial dimensions of Heidou kernels

表2 两品种大豆籽粒次尺寸与主尺寸的关系式 Table 2 Relations between secondary dimension and primary dimension for two varieties of soybean kernels
表3 计算得到的次尺寸与实际大豆籽粒次尺寸之间的比较 Table 3 Comparison between calculated secondary dimension and actual ones
3 大豆籽粒的建模方法

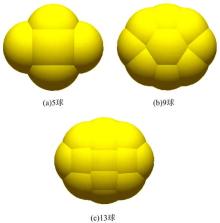
本文提出的单个大豆籽粒的建模方法为:将大豆籽粒简化成椭球形, 椭球的三轴尺寸取实际大豆籽粒群体各三轴尺寸的平均值; 采用球充填方法建立椭球模型。充填球的原则为:充填球的外轮廓尽可能逼近椭球的外轮廓; 充填球的球心落在椭球的轴线或轴平面上; 在满足精度的条件下, 充填球数尽可能少。根据上述原则, 本文提出3种单个大豆籽粒的充填建模方案, 即5球、9球、和13球模型。

图6和图7分别为沂小豆和沂笨豆单个籽粒的3种填充方案。

本文提出的大豆籽粒群体的建模方法为:以上述单个籽粒模型为模板, 选宽度尺寸为主尺寸按正态分布随机产生, 由该宽度尺寸计算得到2个次尺寸, 由这三个尺寸生成每个大豆籽粒模型, 如此反复, 则可建立接近于实际形状和尺寸分布的大豆籽粒群体模型。

图6 沂小豆不同充填球数目的单个籽粒模型Fig.6 Single kernel models of Yixiaodou for various filling spheres

图7 沂笨豆不同充填球数目的单个籽粒模型Fig. 7 Single kernel models of Yibendou for various filling spheres

4 验证与分析

以沂小豆和沂笨豆两个品种大豆籽粒为例, 对本文提出的大豆籽粒建模方法进行试验验证。验证时除采用堆积角的仿真与试验对比外, 本文还采用“ 自流筛分” 过程的仿真与试验对比进行验证。同时加入1个球模型[4]和4球模型[3, 9], 以进行不同充填球数模型的比较。

4.1 试验研究

4.1.1 堆积试验

采用有机玻璃板制成的矩形容器进行大豆籽粒的堆积试验, 如图8所示。

图8 大豆籽粒堆积试验装置Fig.8 Apparatus used for piling tests of soybean kernels

容器的长为340 mm、宽为80 mm、高为330 mm, 有机玻璃板厚度为10 mm。将1 kg大豆籽粒倒入由隔板分成的上方区域, 并使大豆籽粒上表面平整, 然后将中间的插板抽出, 大豆籽粒开始下落堆积直至稳定, 则在上方区域两侧形成堆积角度[10]。用高速摄像记录整个过程, 每种情况进行5次重复试验, 测量上方的堆积角度, 并取5次试验平均值作为该种情况的堆积角。

4.1.2 “ 自流筛分” 试验

本文提出“ 自流筛分” 的验证方法如下。选择长为500 mm、宽为300 mm、厚为1 mm镀锌钢板做成筛板, 如图9所示, 对两品种大豆籽粒进行“ 自流筛分” 试验。其中, 沂小豆籽粒分别采用直径为6.6 mm和6.8 mm的圆孔筛板和尺寸为6.6 mm× 6.6 mm和6.8 mm× 6.8 mm的方孔筛板。沂笨豆籽粒分别采用直径为7.6 mm和7.8 mm的圆孔筛板以及尺寸为7.6 mm× 7.6 mm和7.8 mm× 7.8 mm的方孔筛板。试验前, 将筛板倾斜放置与水平面的夹角为10° , 角度选取可以保证籽粒靠重力沿斜面作自由下滑。在筛板下端放置一个收料盒, 用于收集透筛的大豆籽粒。将总质量为0.5 kg大豆籽粒放置于长度为180 mm、宽度为80 mm、深度为80 mm的给料盒中。给料盒在距筛板顶端40 mm的高度处, 约以0.1 kg/s的速度向筛面释放大豆籽粒, 以保证籽粒与筛面接触时速度较小, 籽粒沿筛面自由下滑。待“ 自流筛分” 过程结束后, 称量收料盒内大豆籽粒的质量, 计算透筛率(透过筛板的大豆籽粒质量占给料的大豆籽粒总质量的百分比), 每种情况重复5次试验, 取5次试验平均值作为该情况的透筛率。

图9 大豆籽粒“ 自流筛分” 试验装置Fig.9 Apparatus used for “ self-flow screening” tests of soybean kernels

4.2 仿真研究

对两个品种大豆籽粒的堆积过程和“ 自流筛分” 过程进行仿真。大豆籽粒模型的充填球数目分别为1、4、5、9、13, 共计5个模型。

仿真采用EDEM v2.5.1软件, 使用Hertz-Mindlin无滑动接触模型。仿真参数选取见表4。其中, 泊松比ν 参考美国农业工程师协会标准取为0.4[11, 12]; 大豆籽粒的密度由液体置换法[13]测量得到; 大豆籽粒与有机玻璃和镀锌钢板之间的静摩擦因数由斜面法[14, 15]测量得到; 根据能量守恒原理[16], 借助高速摄像仪测量了大豆籽粒与有机玻璃和镀锌钢板之间的滚动摩擦因数; 通过挤压试验[17]测得大豆籽粒的弹性模量E, 并根据下式计算出剪切模量G:

G=E/2(1)

采用跌落试验[18]测得大豆籽粒与有机玻璃板和镀锌钢板之间的碰撞恢复系数; 用悬吊碰撞法[19]测得大豆籽粒之间的碰撞恢复系数; 大豆籽粒之间静摩擦因数和滚动摩擦因数在9球模型下通过标定得到; 仿真时步为1× 10-5 s; 仿真时间为6.5 s。

表4 仿真的参数选取 Table 4 Parameters used in simulations

由于EDEM软件的限制, 采用按体积正态分布的方式生成大豆籽粒群体, 其中, 沂小豆籽粒的体积平均值为119.60 mm3、标准差为15.98 mm3; 沂笨豆籽粒的体积平均值为192.03 mm3、标准差为26.34 mm3。

4.3 仿真结果与试验结果的对比分析

4.3.1 堆积试验

图10和图11分别为沂小豆籽粒在4个不同时刻下, 堆积过程的试验照片和仿真截图。

采用2个品种大豆籽粒的10个模型, 仿真的堆积角与试验的堆积角的对比如图12所示。

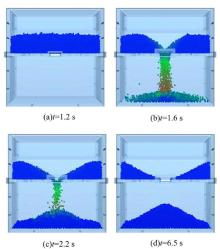图10 沂小豆籽粒堆积过程的试验照片Fig.10 Experimental photos of piling process of Yixiaodou kernels

图11 沂小豆籽粒5球模型堆积过程的仿真截图Fig.11 Snapshots of simulation of piling process of Yixiaodou kernels using 5 sphere model

图12 大豆籽粒堆积角的试验值和仿真值对比Fig.12 Comparison between experimental results and simulated ones of piling angle

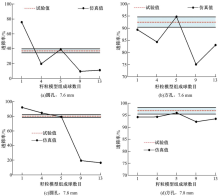
从图12可以看出, 堆积角随籽粒模型组成球数目的增加, 呈先上升后下降的趋势。对于沂小豆籽粒, 当籽粒模型的组成球数目为5时, 堆积角的仿真值在试验值的标准差范围内, 此时仿真和试验堆积角的相对误差为1.79%, 所用的仿真计算时间为2.58 h, 综合考虑相对误差以及计算时间两个方面, 5球充填方案模型较合适。对于沂笨豆, 当籽粒模型的组成球数目为4、5和9时, 对应堆积角的仿真值在试验值的标准差范围内, 此时仿真和试验堆积角的相对误差分别为4.96%、0.44%和0.32%, 所用的仿真计算时间分别为1.23、1.4和2.38 h, 而5球和9球的相对误差较小, 但5球所用的仿真计算时间要比9球小很多, 综合考虑相对误差以及计算时间两方面, 可知5球模型较合适。

4.3.2 “ 自流筛分” 试验

图13和图14分别为沂小豆籽粒在筛孔直径为6.6 mm的圆孔筛上“ 自流筛分” 试验结束后的试验照片和仿真截图。

图13 沂小豆籽粒“ 自流筛分” 试验照片Fig.13 Experimental photo of “ self-flow screening” process of Yixiaodou kernels

图14 沂小豆籽粒5球模型“ 自流筛分” 的仿真截图Fig.14 Snapshot of simulation of “ self-flow screening” process of Yixiaodou kernels using 5 sphere model

将2个品种大豆籽粒分别采用5种充填建模方案进行仿真, 其透筛率的仿真值与试验值对比如图15和图16所示。

图15 沂小豆籽粒透筛率试验值和仿真值对比Fig.15 Comparisons between experimental results and simulated ones of percentages passing of Yixiaodou

图16 沂笨豆籽粒透筛率试验值和仿真值对比Fig.16 Comparisons between experimental results and simulated ones of percentages passing of Yibendou

从图15和图16可以看出, 当籽粒模型充填球数为5时, 对应透筛率的取值在试验值的标准差范围内, 也就是说, 用球充填建立大豆籽粒模型时, 5球模型效果较好。

为了进一步验证上述结论, 对“ 自流筛分” 的收料盒进行分区, 如图17和18所示, 重新对两品种大豆籽粒进行“ 自流筛分” 试验, 并计算各区的透筛率。同时以5球模型为对象, 进行了仿真并与试验对比, 其他条件与上述相同。图17和图18分别为沂小豆籽粒在筛孔直径为6.6 mm的圆孔筛上不同区域透筛过程的试验照片和仿真截图。

图19和图20为仿真与试验对比。由图可知, 仿真和试验后各收料区域内的透筛情况较为一致。由此进一步证明了5球模型的可行性和有效性。

图17 沂小豆籽粒“ 自流筛分” 分区试验照片Fig.17 Experimental photo of partitioned “ self-flow screening” process of Yixiaodou kernels

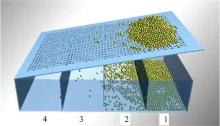图18 沂小豆籽粒5球模型“ 自流筛分” 分区的仿真截图Fig.18 Snapshot of simulation of partitioned “ self-flow screening” process of Yixiaodou kernels using a 5 sphere model

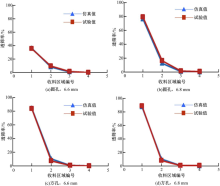图19 沂小豆籽粒各收料区透筛率试验值与仿真值对比Fig.19 Comparisons between experimental results andsimulated ones of percentages passing of Yixiaodou kernels for different collecting bins

图20 沂笨豆籽粒各收料区透筛率试验值与仿真值对比Fig.20 Comparisons between experimental results and simulated ones of percentages passing of Yibendou kernels for different collecting bins

5 结 论

(1)大豆籽粒形状与椭球形比较近似, 大豆籽粒建模时可简化成椭球形, 采用球充填方法建立单个大豆籽粒(椭球)的分析模型。

(2)大豆籽粒的三轴尺寸均服从正态分布, 三轴尺寸间存在一定函数关系; 选单个大豆籽粒模型(椭球)的主尺寸, 按正态分布随机产生, 次尺寸根据与主尺寸的关系计算得出, 由这三个尺寸生成每个大豆籽粒模型, 由此建立接近于实际尺寸分布的大豆籽粒群体模型。

(3)当充填球数目为5时, 堆积试验和本文提出的“ 自流筛分” 试验结果与仿真结果较为接近, 证明了本文提出的5球充填的大豆籽粒模型较合适, 初步证明了本文提出的大豆籽粒建模方法的可行性和有效性。

The authors have declared that no competing interests exist.

参考文献
[1] Cundall P A, Strack O L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65. [本文引用:1]
[2] 于建群, 付宏, 李红, 等. 离散元法及其在农业机械工作部件研究与设计中的应用[J]. 农业工程学报, 2005, 21(5): 1-6.
Yu Jian-qun, Fu Hong, Li Hong, et al. Application of discrete element method to research and design of working parts of agricultural machines[J]. Transactions of the Chinese Society of Agricultural Engineering, 2005, 21(5): 1-6. [本文引用:1]
[3] Vu-Quoc L, Zhang X, Walton O R. A 3-D discrete-element method for dry granular flows of ellipsoidal particles[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 187: 483-528. [本文引用:3]
[4] Boac J M, Casada M E, Maghirang R G, et al. Material and interaction properties of selected grains and oilseeds for modeling discrete particles[J]. Transactions of the ASABE, 2010, 53(4): 1201-1216. [本文引用:4]
[5] Tao H, Zhong W, Jin B. Comparison of construction method for DEM smulation of ellipsoidal particles[J]. Chinese Journal of Chemical Engineering, 2013, 21(7): 800-807. [本文引用:3]
[6] Li Z Q, Yu J Q, Feng Z R, et al. Simulation and performance analysis of a soybean seed metering device using discrete element method[J]. Sensor Letters, 2013, 11: 1217-1222. [本文引用:1]
[7] Lu Z, Negi S C, Jofriet J C. A numerical model for flow of granular materials in silos. Part 1: model development[J]. Journal of Agricultural Engineering Research, 1997, 68: 223-229. [本文引用:1]
[8] Markauskas D, Kaianauskas R, Džiugys A, et al. Investigation of adequacy of multi-sphere approximation of elliptical particles for DEM simulations[J]. Granular Matter, 2010, 12: 107-123. [本文引用:1]
[9] 赵历. 组合椭球颗粒模型的三维离散单元法的研究[D]. 长春: 吉林大学计算机科学与技术学院, 2010.
Zhao Li. Research of three-dimensional discrete element method based on combination ellipsoid particle model[D]. Changchun: Collegc of Computer Science and Technology, Jilin University, 2010. [本文引用:1]
[10] Zhou Y C, Wright B D, Yang R Y, et al. Rolling friction in the dynamic simulation of sand pile formation[J]. Physica A, 1999, 269: 536-553. [本文引用:1]
[11] Coşkun M B, Yalçin Ì, Özarslan C. Physical properties of sweet corn seed (Zea mays saccharata Sturt)[J]. Journal of Food Engineering, 2006, 74(4): 523-528. [本文引用:1]
[12] ASAE. S368. 4 DEC2000(R2006). Compression test of food materials of convex shape[S]. [本文引用:1]
[13] Kibar H, Öztürk T. Physical and mechanical properties of soybean[J]. International Agrophysics, 2008, 22: 239-244. [本文引用:1]
[14] González-Montellano C, Fuentes J M, Ayuga-Téllez E, et al. Determination of the mechanical properties of maize grains and olives required for use in DEM simulations[J]. Journal of Food Engineering, 2012, 111: 553-562. [本文引用:1]
[15] 张列男. 基于离散元法的大豆精密排种器的数字化设计方法研究[D]. 长春: 吉林大学生物与农业工程学院, 2009.
Zhang Lie-nan. Digital design method of soybean precision seed-metering device based on DEM[D]. Changchun: College of Biological and Agricultural Engineering, Jilin University, 2009. [本文引用:1]
[16] 崔涛, 刘佳, 杨丽, 等. 基于高速摄像的玉米种子滚动摩擦特性试验与仿真[J]. 农业工程学报, 2013, 29(15): 34-41.
Cui Tao, Liu Jia, Yang Li, et al. Experiment and simulation of rolling friction characteristic of corn seed based on high-speed photography[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(15): 34-41. [本文引用:1]
[17] Misra R N, Young J H. A model for predicting the effect of moisture content on the modulus of elasticity of soybeans[J]. Transactions of the ASAE, 1981, 24(5): 1338-1341. [本文引用:1]
[18] LoCurto G J, Zhang X, Zakirov V, et al. Soybean impacts: experiments and dynamic simulations[J]. Transactions of the ASAE, 1999, 40(3): 789-794. [本文引用:1]
[19] Wong C X, Daniel M C, Rongong J A. Energy dissipation prediction of particle dampers[J]. Journal of Sound and Vibration, 2009, 319: 91-118. [本文引用:1]