引用本文
王旭, 欧阳继红, 陈桂芬. 基于多重序列所有公共子序列的启发式算法度量多图的相似度. 2018, 48(2): 526-532
WANG Xu, OUYANG Ji-hong, CHEN Gui-fen. Heuristic algorithm of all common subsequences of multiple sequences for measuring multiple graphs similarity. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 526-532  
Doi:10.13229/j.cnki.jdxbgxb20170302
Permissions
Copyright©2018, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于多重序列所有公共子序列的启发式算法度量多图的相似度
王旭1,2, 欧阳继红1,2, 陈桂芬3
1.吉林大学 计算机科学与技术学院,长春130012
2.吉林大学 符号计算与知识工程教育部重点实验室,长春130012
3.吉林农业大学 信息技术学院,长春 130118
通信作者:欧阳继红(1964-),女,教授,博士生导师. 研究方向:数据挖掘,时空推理. E-mail:ouyj@jlu.edu.cn

作者简介:王旭(1982-),男,博士研究生. 研究方向:数据挖掘,图挖掘. E-mail:75014557@qq.com

基金项目:国家自然科学基金项目(61472157,61602204,6152198)
摘要

提出了启发式A*算法度量任意多个图的相似度方法,该算法将多图表示多重序列,在多重序列的匹配点上计算多重序列的所有公共子序列数,得到的所有公共子序列数用来度量多图的相似度。该算法避免了在非匹配点上的冗余计算,最大化后缀序列的所有公共子序列数的启发函数值,将访问的节点限制在两个序列匹配的子集,减少了计算节点的个数。与现有度量图的相似度方法相比,该算法不仅可以度量任意多个图的相似度,而且计算过程简单,通过启发信息的引导能够快速地度量多图的相似度。

关键词: 人工智能; 多图相似度; 启发式算法; 所有公共子序列; 多重序列; 匹配
中图分类号:TP18 文献标志码:A 文章编号:1671-5497(2018)02-0526-07
Heuristic algorithm of all common subsequences of multiple sequences for measuring multiple graphs similarity
WANG Xu1,2, OUYANG Ji-hong1,2, CHEN Gui-fen3
1.College of Computer Science and Technology, Jilin University, Changchun 130012, China
2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University, Changchun 130012, China
3.College of Information Technology, Jilin Agricultural University, Changchun 130118, China
Abstract

A heuristic algorithm A* for measuring the similarity of multiple graphs is proposed. In this algorithm, the multiple graphs are represented as multiple sequences, then the number of all common subsequences in the matches of the multiple graphs is calculated, and this number is used to measure the similarity of the multiple graphs. This algorithm avoids the redundant calculations in non-matches of multiple graphs, maximizes the heuristic function value of all common subsequences of the suffixes sequences, limits the search nodes to the subset of matches between two sequences, thus reducing the number of the calculation nodes. Compared with the existing graph similarity methods, the proposed algorithm can not only measure the similarity of multiple graphs, but also simplify the calculation process. The similarity of multiple graphs can be quickly measured using this algorithm with the boot of the heuristic information.

Key words: artificial intelligence; multiple graph similarity; heuristic algorithm; all common subsequences; multiple sequences; matches
0 引 言

图是最重要和值得深入研究的数据结构之一, 例如在生物信息学和化学领域中, DNAs和分子都是以图的结构出现的[1, 2]。在分析这种图数据类型时, 度量图的相似度承担了一个重要角色[3, 4], 图的相似度度量方法能够处理这些领域的图数据, 对DNAs和分子进行提取和分类, 有效地解决分类问题。随着图数据日益增加及其复杂性, 需要更加有效的方法处理任意多个图的相似度方法[5, 6], 而现有的大部分度量图的相似度方法都是度量两个图的相似度[7, 8]。图相似度度量方法可将图表示为序列[9, 10, 11], 用度量序列的方法度量图的相似度。度量序列相似度方法可以采用所有公共子序列方法(All common subsequences, ACS)[12, 13]。ACS方法通过计算所有公共子序列数度量序列的相似度, 与最长公共子序列方法相比, ACS不仅包含了最长的公共子序列, 而且包含了第二长、第三长、……的公共子序列, 最大化地获取公共子序列的信息, 更能反映出序列间的相似程度。所有公共子序列数越大, 序列相似度越大; 反之, 序列相似度越小。度量序列的相似度也可以采用启发式方法, 在查找多重序列的匹配时, 最大化启发估计值, 以便最少地扩展节点, 进而找到最优解。但现有的启发式算法提出的公共子序列只包含一个字符, 不适应实际的应用[14], 查找最长公共子序列的启发式算法[15], 不如ACS方法更能反映出序列之间的相似程度。为度量多图的相似度, 如何将图表示为包含更多原图信息的对应序列, 并应用启发函数减少扩展节点的个数, 成为度量多图相似度的重要问题。

本文提出了多重序列所有公共子序列的启发式算法度量多图的相似度, 将多图表示多重序列, 当多重序列的一个匹配出现时, 该算法递归地计算在匹配点上的所有公共子序列数, 通过下标比较查找多重序列的公共子序列、剔除重复的匹配, 通过后缀序列的启发函数减小计算多重序列的所有公共子序列数的节点个数, 有效地解决任意多个图的相似度问题。

1 图表示为序列
1.1 图表示序列方法

将图表示为序列, 序列要保留原图的信息, 这样通过度量序列的相似度度量图的相似度时, 度量结果才能保证图的相似度的准确性。本文采用图的深度优先搜索方法, 以任一顶点作为序列的初始节点, 按照该顶点与其它顶点间的路径搜索, 将图表示为顶点序列。顶点序列体现了图中顶点访问的层次顺序, 反映了顶点间的路径信息以及连通性, 较好地保留了图的信息。在搜索顶点时, 若某一顶点已访问过, 就不再从该顶点出发进行搜索, 搜索图的过程实质上是对每个顶点查找其邻接顶点的过程。为保证度量的准确性, 选择图中相同或相似位置的顶点作为序列的初始节点。应用图深度优先搜索方法可将d个图G1, G2, …, Gd表示为d个序列, 这些d个序列组成集合S = {s1, s2, …, sd}, S为字母表Σ 上的多重序列(multiple sequences), d ≥ 2。本文研究的图是顶点带标号的有向图。

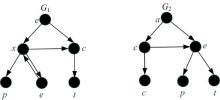
以两个图G1和G2(如图1所示)为例, 选取具有相同结构的顶点(e和a)为序列的初始节点, 应用图深度优先搜索方法将G1和G2表示为对应顶点序列s1和s2, s1= expect, s2=accept。

图1 有向图G1和G2Fig.1 The directed graphs G1and G2

1.2 所有公共子序列方法

所有公共子序列方法(ACS)可以度量序列的相似度, 所有公共子序列数越大, 序列的相似度越大; 反之, 序列的相似度越小。下面给出d个序列的所有公共子序列的定义, d ≥ 2。

定义1 从序列s中删除0个或更多的元素所获得的序列称为s的子序列:

(1)若序列x为si的子序列, 1 ≤ i ≤ d, 则称x为多重序列S的公共子序列;

(2)满足(1)的情况下所有的x称为S的所有公共子序列。用|MACS|表示S的所有公共子序列数。

为度量多重序列S的相似度, 应用所有公共子序列方法计算|MACS|, |MACS|越大, 多重序列的相似度越大; 反之, 多重序列的相似度越小。以两个序列s1, s2为例, 长度分别为n1, n2, ACS(x, y)表示s1和s2所有公共子序列数, 有下式成立。

ACS= 1　　　　　　　　　　ifxory=02×ACSx-1, y-1ifs1[x]=s2[y]ACSx-1, y+ACSx, y-1-　　ACSx-1, y-1ifs1[x]≠s2[y] (1)

式中:当x = 0或y = 0时, s1和s2的公共子序列仅有空集∅, 所以ACS(0, y) = 1, ACS(x, 0) = 1和ACS(0, 0) = 1; 当s1[x]= s2[y]时, s1[x]或s2[y]成为s1和s2新的公共子序列, s1[x]或s2[y]与ACS(x - 1, y - 1)已得到的公共子序列组成新的公共子序列, 新的公共子序列数为ACS(x - 1, y - 1), 在s1[x]或s2[y]点上的所有公共子序列数是ACS(x - 1, y - 1)的2倍, 所以ACS(x, y) = ACS(x - 1, y - 1) × 2, 0 ≤ x ≤ n1, 0 ≤ y ≤ n2。公式(1)迭代地建立n1× n2矩阵M, 计算s1和s2的所有公共子序列数, ACS(x, y)值越大, s1和s2越相似。

对于图1中G1和G2的对应序列s1=expect和s2=accept, 由公式(1)计算得到的所有公共子序列数如表1所示, s1和s2的所有公共子序列为:{∅, e, p, c, t, ct, ep, et, pt, ept}, s1和s2所有公共子序列数ACS(s1, s2) = 10。

表1 s1和s2的所有公共子序列数 Table 1 The number of all common subsequences between s1 and s2
2 ACS的启发式方法

多重序列表示为S = {s1, s2, … , sd}, d ≥ 2, 对应的长度分别为n1, n2, … , nd。S中长度分别为ni, nj任意两个序列si和sj的后缀序列为:si[x+1, … , ni]和sj[y+1, … , nj], 0 ≤ x ≤ ni, 0 ≤ y ≤ nj, 0 ≤ i, j ≤ d, ACSsuf(x, y)ij表示两个后缀序列的所有公共子序列数, 有下式成立:

ACSsuf x, yij= 0　　　　　　　　　　　ifx=niory=nj2×ACSsuf(x+1, y+1)ijifsi[x+1]=sj[y+1]ACSsuf(x, y+1)ij+ACSsuf(x+1, y)ij-　　ACSsuf(x, y)ijifsi[x+1]≠sj[y+1] (2)

式中:当x = ni或y = nj, si和sj没有后缀序列, 所以ACSsuf(ni, y)ij = 0, ACSsuf(x, nj)ij = 0和ACSsuf(ni, nj)ij = 0; 当si[x+1] = sj[y+1]时, si[x+1]或sj[y+1]与ACSsuf(x+1, y+1)ij得到的公共子序列组成新的公共子序列, 所以ACSsuf(x, y)ij = ACSsuf(x+1, y+1)ij × 2。公式(2)迭代地建立(ni - x) × ( nj - y)矩阵Msuf, 计算si和sj后缀序列的所有公共子序列数, ACSsuf(x, y)ij值越大, si和sj后缀序列越相似。

p表示多重序列S上的点, p = (p1, p2, …, pi, …, pd), 1 ≤ i ≤ d, 1 ≤ pi≤ ni, pi表示序列ni上的点, ni表示ni的长度。对于点p的d个后缀序列si[pi+1, … , ni], 可以应用公式(2)计算这些后缀序列的所有公共子序列数, h* (p)表示任意两个后缀序列si[pi+1, … , ni]和sj[pj+1, … , nj]的所有公共子序列数, 1 ≤ i, j ≤ d, 有下式成立。

h* (p)= min1≤i, j≤dACSsuf pi, pj (3)

定理1 若h(p)表示d个后缀序列s1[p1+1, …, n1], s2[p2+1, …, n2], …, si[pi+1, …, ni], …, sd[pd+ 1, …, nd]的所有公共子序列数, 1 ≤ i ≤ d, 则h(p) ≤ h* (p)。

证明:d个后缀序列的所有公共子序列是d中任意两个序列最少的所有公共子序列的子集, d个后缀序列的所有公共子序列数小于等于d中任意两个序列的所有公共子序列数的最小值, 由公式(3)可知, h* (p)表示任意两个序列的所有公共子序列数的最小值, h* (p)肯定大于等于d个后缀序列的所有公共子序列数h(p), 即h(p) ≤ h* (p), 得证。

若s1[p1] = s2[p2] =…= si[pi] =…= sd[pd], 称点p = (p1, p2, …, pi, …, pd)为多重序列S上的一个匹配。对于图1中G1和G2的对应序列 s1=expect和s2=accept, 点(4, 4)为s1和s2在字符e的匹配, (5, 3)为s1和s2在c的匹配, s1和s2的所有匹配出现的位置如表2所示。

表2 s1和s2匹配出现的位置 Table 2 The locations of the matches between s1 and s2

定义2 对于多重序列S上的两个点p = (p1, p2, …, pi, …, pd), q = (q1, q2, …, qi, …, qd), 如果满足pi< qi, 1≤ i≤ d, 则称p的所有下标对应地小于q的所有下标, 记Subscript(p) < Subscript(q)。

若p和q为S上的两个匹配, Combine(p, q)表示p和q的合并后的序列:

Combine(p, q)= pq　ifSubscript(p)< Subscript(q)qpifSubscript(p)> Subscript(q) (4)

对于图1中G1和G2的对应序列s1和s2, (1, 4)和(3, 5)分别为字符e和p的匹配, 且Subscript(e) < Subscript(p), 合并(1, 4)和(3, 5)得到的序列为:Combine((1, 4), (3, 5)) = Combine(e, p) = (ep)。

定理2 若点p和q为S上的两个匹配, 则Combine(p, q)为S的公共子序列。

证明:根据定义2和公式(4), 当q的所有下标对应地大于p的所有下标, 即pi< qi, 或q的所有下标对应地小于p的所有下标, 即qi< pi, 才可以合并p和q。点p和q为S上的匹配, 则p和q分别为S的公共子序列, 对于si上的点pi和qi, pi和qi分别为S的公共子序列, 当pi< qi或qi< pi, 则序列(piqi)或(qipi)也是S的公共子序列, 1≤ i ≤ d。所以合并p和q的序列Combine(p, q)为S的公共子序列, 得证。

合并两个匹配可以得到公共子序列, 当新的匹配出现, 如果新的匹配的下标大于或小于合并后序列的下标, 就会产生新的公共子序列, 所以需要标记合并后序列的下标。合并后的序列Combine(p, q)的下标为p和q中最大的下标, 有下式成立。

Subscript(Combine(p, q))= Subscript(q)　ifSubscript(p)< Subscript(q)Subscript(p)ifSubscript(p)> Subscript(q) (5)

对于图1中G1和G2的对应序列s1和s2, (1, 4)为字符e的匹配, (3, 5)为字符p的匹配, 合并后的序列(ep)的下标Subscript(ep) = Subscript(p) = (3, 5)。

由定理2可知, 当Combine(p, q)为S的公共子序列, Combine(p, q)可以看作S上新的匹配, Combine(p, q)下标为p和q中最大的下标, 所以有:

推论1 点p, q, r为S上的匹配, 若Subscript(r) > Subscript(q) > Subscript(p), 则(pqr)为S的公共子序列。

对于图1中的s1和s2, (1, 4)为字符e的匹配, (3, 5)为字符p的匹配, (6, 6)为字符t的匹配, 合并后的序列(ept)为S的公共子序列。

定义3 设f(n) = g(n) + h(n), g(n)表示从初始节点到节点n付出的实际代价, h(n)表示从节点n到目标节点的最优路径的估计代价, 称使用f(n)作为估价函数的GRAPHSEARCH算法为A。若算法A中使用的启发函数h(n)对任何节点都有h(n) ≤ h* (n), 则称其为A* 算法。

|MACS|表示多重序列(s1, s2, … , sd)的所有公共子序列数, d ≥ 2, f(p)表示d个序列(s1, s2, … , sd)的|MACS|的估计函数, g(p)表示d个前缀序列s1[1, … , p1], s2[1, … , p2], …, si[1, … , pi], …, sd[1, … , pd]的|MACS|, g(p)可由公式(1)计算, h(p)表示d个后缀序列s1[p1+1, … , n1], s2[p2+1, …, n2], …, si[pi+1, … , ni], …, sd[pd+ 1, … , nd]的|MACS|, 1 ≤ i ≤ d, h(p)可由公式(2)计算, 所以|MACS|的估计函数为:

f(p)=g(p)+h(p) (6)

h* (p)表示d中任意两个后缀序列si[pi+1, …, ni]和sj[pj+1, …, nj]的|MACS|的估计函数, 1≤ i, j≤ d, h* (p)可由公式(3)计算。用h* (p)代替h(p)计算后缀序列的|MACS|, |MACS|的估计函数变成:

f* (p)=g* (p)+h* (p) (7)

定理3 计算|MACS|的估计函数f* (p)是A* 算法。

证明:由公式(7)可知, f* (p) = g* (p) + h* (p), f* (p)表示从初始节点出发经由节点p到达目标节点的所有公共子序列数的估计函数, g* (p)表示从初始节点到节点p的所有公共子序列数, h* (p)表示从节点p到目标节点的所有公共子序列数的估计函数。由定理1可知h(p) ≤ h* (p), 根据定义2, f* (p)是A* 算法, 得证。

用MACS-A* 表示计算|MACS|的估计函数f* (p), 与A* 算法查找最短搜索路径不同, MACS-A* 是在d维矩阵里计算d个序列的所有公共子序列数。MACS-A* 是A* 算法的变形, 在每次计算点p位置的所有公共子序列数时, 最大化启发函数h* (p)。h* (p)越大, 包含的启发信息越多, 所需计算的节点越少, 更快地找到目标节点, 计算所有公共子序列数。若h* (p) = 0, 点p到达目标节点, f* (p) = g* (p) + h* (p) = g* (p) =|MACS|, 所以有:

推论2 若h* (p) = 0, 则g* (p) =|MACS|。

3 度量多图相似度算法MACS-A*

通过计算多重序列的所有公共子序列数可以度量多重序列的相似度, 根据将多图表示为多重序列的图深度优先搜索方法, 度量多重序列的相似度可以度量多图的相似度, 所以, 计算多重序列的所有公共子序列数可以度量多图的相似度, 度量图的相似度问题简化为计算所有公共子序列数的问题。多重序列的所有公共子序列数越大, 多图的相似度越大; 反之, 相似度越小。因此, 本文提出了计算多重序列所有公共子序列数的启发式算法MACS-A* , 通过计算d个序列的前缀序列和后缀序列的所有公共子序列数度量d个图的相似度, d≥ 2。

MACS-A* 算法从初始点p0=(0, 0, …, 0)开始, 计算d个序列的所有单个字符的匹配, 放在集合Q中。从表1可以看出, 当一个匹配出现时, 该匹配为多重序列的公共子序列, 且该匹配与之前的公共子序列组成新的公共子序列。但对于表2圆圈中标记的匹配位置, 该匹配已经出现, 与之前的公共子序列组成新的公共子序列也已经出现, 而且公式(2)在该匹配计算的所有公共子序列数并没有变化。因为圆圈中匹配的下标不大于之前出现过的匹配的下标, 所以当圆圈中的匹配出现时, 不能组成新的公共子序列。对于圆圈中的匹配, 在查找所有公共子序列和计算所有公共子序列数时, 通过下标比较, 不对该匹配进行合并序列、标记下标操作。

MACS-A* 算法首先应用图深度优先搜索方法将d个图表示为d个序列; 接着从Q中提取一个匹配p, T为d个序列的所有公共子序列的集合, 比较p与Q、T中的序列的下标, 合并序列后组成新的公共子序列, 并对新的公共子序列标记下标, 将不重复新的公共子序列放在T中; 然后用公式(7)计算d个序列的所有公共子序列数, 其中f* (p)表示d个序列的所有公共子序列数估计函数, g* (p)表示d个前缀序列的所有公共子序列数, h* (p)表示d个后缀序列的所有公共子序列数的启发函数; 最后返回d个序列的所有公共子序列和所有公共子序列数。

算法1:MACS-A* (s1, s2, …, sd)算法

输入:图G1, G2, …, Gd

输出:d个图的所有公共子序列和所有公共子序列数

步骤1:应用图深度优先搜索方法将d个图表示为d个序列(s1, s2, …, sd), d ≥ 2;

步骤2:初始p0= (0, 0, …, 0), g* (p0) = 0, f* (p0) = h* (p0), 集合T表示d个序列的所有公共子序列, 初始T = {∅}, 空集的下标Subscript(∅) = (0, 0, … , 0);

步骤3:计算d个序列的所有匹配, 并放入Q中;

步骤4:|Q|表示d个序列的所有匹配数, 从Q中取出一个匹配p, q表示Q中的任一匹配, t表示T中任一公共子序列, 若|Q| > 0, 转到步骤5, 否则, 转到步骤10;

步骤5:比较p和q的下标, 若Subscript(p) > Subscript(q), 否则, 转到步骤6, 合并p和q, Combine(q, p) = (qp), 并用p的下标标记(qp)的下标, Subscript(qp) = Subscript(p), 若(qp)不在T中, Label(qp) Ï Label(t), 将(qp)放入T中, T = T + {qp}, 转到步骤7;

步骤6:若Subscript(p) < Subscript(q), 合并p和q, Combine(q, p) = (pq), 并用q的下标标记(pq)的下标, Subscript(pq) = Subscript(q), 若(pq)不在T中, Label(pq) Ï Label(t), 将(pq)放入T中, T = T+ {pq}, 转到步骤7;

步骤7:若p不在T中, label(p) Ï label(t), 将p并入T中, T= T+ {p}, 计算d个序列的所有公共子序列数, f* (p) = g* (p) + h* (p), 转到步骤8;

步骤8:比较p和t的下标, 若Subscript(p) > Subscript(t), 将合并p和t的序列(tp)并入T中, T = T + {tp}, 标记(tp)的下标, Subscript(tp) = Subscript(p), 转到步骤9;

步骤9:从Q中删除p, Q = Q - {p}, 转到步骤4;

步骤10:输出T和f* (p), T为d个序列的所有公共子序列集合, 包括空集, f* (p)为d个序列的所有公共子序列数。

算法1包括两部分:将d个图G1, G2, …, Gd表示为d个序列(s1, s2, …, sd), d ≥ 2; 计算d个序列的所有公共子序列数, 并输出所有公共子序列。为了方便分析算法1的时间复杂度, 设d个图的顶点数均为n, 则d个序列(s1, s2, …, sd)的长度均为n。

算法1的步骤1应用图深度优先搜索方法将顶点带标号的有向图G表示为序列s, 时间复杂度为O(n +|E|), 其中n和|E|分别表示G的顶点数和边数。图深度优先搜索方法将d个图表示为d个序列的时间复杂度为O(dn + d|E|)。若|E| = n × (n - 1) = (n2- n), 则G为完全有向图。最坏情况下, 将d个图表示为d个序列的时间复杂度为O(dn + d(n2- n))= O(dn2)。

算法1的步骤3为计算d个序列的所有匹配, 从表1可以看出, 建立2维矩阵Mij需要O(n2)的时间复杂度, 1 ≤ i, j ≤ d。从矩阵Mij可看出, 计算2个序列中的所有匹配, 需要O(n2)的时间复杂度, 计算d个序列的所有匹配, 需要O(dn2)的时间复杂度。

在算法1的步骤4中, Q为d个序列的所有单个字符匹配的集合, |Q|最大为n, n表示序列si的长度, 1 ≤ i ≤ d。步骤5、步骤6和步骤8为比较p和Q中匹配的下标、p和T中的公共子序列的下标, 时间复杂度为O(d)。步骤7为避免重复序列出现在T中, 比较新组成的公共子序列与T中序列的字符, 判断新的序列是否存在T中, 新的序列最长为n, 最多为|Σ |个字符, Σ 表示字母表, 比较序列字符的时间复杂度为O(n|Σ |)。当新组成的公共子序列出现时, 对p与Q中的每个匹配、T中的公共子序列进行合并和标记下标, 其操作的时间复杂度为O(1)。所以, 处理点p的时间复杂度总共为O(dn|Σ |)。步骤9从Q中删除点p, 当执行完步骤4, Q为空, 所需的时间复杂度为O(dn2|Σ |)。

点p0从(0, 0, … , 0)到(n, n, … , n), 当处理d个序列的每个匹配时, 用公式(1)和公式(3)递归地计算d个序列在点p的所有公共子序列数f* (p) = g* (p) + h* (p), 其时间复杂度也为O(dn2|Σ |)。结合步骤3的时间复杂度, 用MACS-A* 算法查找d个序列的所有公共子序列的时间复杂度为O(dn2+ dn2|Σ |), 递归地计算d个序列的所有公共子序列数f* (p)的时间复杂度也为O(dn2+ dn2|Σ |)。

所以, 结合步骤1的时间复杂度, 用MACS-A* 算法度量d个图的相似度的时间复杂度为O(dn2+ dn2+ dn2|Σ |)。

4 结束语

本文提出的启发式算法MACS-A* 通过计算多重序列的所有公共子序列数度量多图的相似度, 由于所有公共子序列数的变化都是在多重序列的匹配出现之后, 所以MACS-A* 算法递归地计算在匹配点上的所有公共子序列数, 不必计算所有点的公共子序列数, 避免了在非匹配点上冗余计算。该算法在处理匹配的过程中最大化后缀序列的启发函数值h* (p), 将访问的匹配点p限制在矩阵M(公式(1))的匹配的子集, 通过下标比较剔除不能组成新的公共子序列的匹配, 进一步减少了计算节点的个数, 能够快速地度量多图的相似度。

The authors have declared that no competing interests exist.

参考文献
[1] Hattori M, Okuno Y, Goto S, et al. Development of a chemical structure comparison method for integrated analysis of chemical and genomic information in the metabolic pathways[J]. Journal of the American Chemical Society, 2003, 125(39): 11853-11865. [本文引用:1]
[2] Shanavas N, Wang H, Lin Z, et al. Supervised graph-based term weighting scheme for effective Text Classification[C] ∥ Proceedings of the 22nd European Conference on Artificial Intelligence, Hague, Netherland s, 2016: 1710-1711. [本文引用:1]
[3] Elzinga C, Wang H. Kernels for acyclic digraphs[J]. Pattern Recognition Letters, 2012, 33(16): 2239-2244. [本文引用:1]
[4] Sugiyama M, Llinares F, Kasenburg N, et al. Significant subgraph mining with multiple testing correction[C] ∥ Proceedings of the SIAM International Conference on Data Mining, Vancouver, Canada, 2015: 37-45. [本文引用:1]
[5] Li Tao, Dong Han, Shi Yong-tang, et al. A comparative analysis of new graph distance measures and graph edit distance[J]. Information Sciences, 2017, 403: 15-21. [本文引用:1]
[6] Zhu Gang-gao, Iglesias C. Computing semantic similarity of concepts in knowledge graphs[J]. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(1): 72-85. [本文引用:1]
[7] Sugiyama M, Borgwardt K. Halting in rand om walk Kernels[C]∥28th International Conference on Neural Information Processing Systems, Montreal, Canada, 2015: 1639-1647. [本文引用:1]
[8] Borgwardt K, Kriegel H. Shortest-path Kernels on graphs[C]∥Proceedings of IEEE International Conference on Data Mining, Houston, USA, 2005: 74-81. [本文引用:1]
[9] Szilagyi S, Szilagyi L. A fast hierarchical clustering algorithm for large-scale protein sequence data sets[J]. Computers in Biology and Medicine, 2014, 48: 94-101. [本文引用:1]
[10] Forster D, Bittner L, Karkar S, et al. Testing ecological theories with sequence similarity networks: marine ciliates exhibit similar geographic dispersal patterns as multicellular organisms[J]. BMC Biology, 2015, 13(1): 1-16. [本文引用:1]
[11] Yanardag P, Vishwanathan S. A structural smoothing framework for robust graph comparison[C]∥Proceedings of Neural Information Processing Systems, Montreal, Canada, 2015: 2134-2142. [本文引用:1]
[12] Wang H. All common subsequences[C]∥Proceeding 20th International Joint Conference on Artificial Intelligence, Hyderabad, India, 2007: 635-640. [本文引用:1]
[13] Lin Z, Wang H, McClean S. A multidimensional sequence approach to measuring tree similarity[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(2): 197-208. [本文引用:1]
[14] Chin F, Poon C. Performance analysis of some simple heuristics for computing longest common subsequences[J]. Algorithmica, 1994, 12: 293-311. [本文引用:1]
[15] Wang Q, Korkin D, Shang Y. A fast multiple longest common subsequence(MLCS) algorithm[J]. IEEE Transactions on Knowledge and Data Engineering, 2011, 23(3): 321-334. [本文引用:1]