量子k-means算法

引用本文

刘雪娟, 袁家斌, 许娟, 段博佳. 量子k-means算法. 2018, 48(2): 539-544
LIU Xue-juan, YUAN Jia-bin, XU Juan, DUAN Bo-jia. Quantum k-means algorithm. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 539-544 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170051
Permissions

量子k-means算法

刘雪娟, 袁家斌, 许娟, 段博佳

南京航空航天大学计算机科学与技术学院,南京 210016

作者简介:刘雪娟(1980-),女,博士研究生.研究方向:量子计算, 数据挖掘.E-mail:liu_juanjuan80@126.com

基金项目:国家自然科学基金项目(61571226); 江苏省自然科学基金项目(BK20140823)

摘要

为提高经典k-means算法的计算效率,引入量子计算理论得到量子k-means算法。先将聚类数据和 k个聚类中心制备成量子态,并行计算其相似度,接着利用相位估计算法将相似度信息保存到量子比特中,然后利用最小值查找量子算法查找最相似的聚类中心点。对比两种算法的复杂度可知,在一定条件下,相对经典算法而言,量子k-means算法的时间复杂度降低,空间复杂度得到指数级降低。

关键词: 人工智能; 聚类; 量子计算; 量子算法; 量子k-means

中图分类号:TP387 文献标志码:A 文章编号:1671-5497(2018)02-0539-06

Quantum k-means algorithm

LIU Xue-juan, YUAN Jia-bin, XU Juan, DUAN Bo-jia

College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Abstract

In this paper a quantum k-means algorithm is proposed by integrating the quantum paradigm to improve the efficiency of traditional k-means algorithm. First, each vector and k cluster centers are prepared to be in quantum superposition, which are then utilized to compute the similarities in parallel. Second, the quantum amplitude estimation algorithm is applied to convert the similarities into quantum bit. Finally, from the quantum bit the most similar center of the vector is obtained using the quantum algorithm for determining the minimum. Theoretical analysis shows that, compared with the traditional quantum algorithm, the time complexity of the quantum k-means algorithm decreases under given condition and the space complexity diminishes exponentially.

Key words: artificial intelligence; clustering; quantum computation; quantum algorithm; quantum k-means

Show Figures

0 引言

近年来, 越多越多的学者将量子计算应用于数据挖掘领域^[1]。 Anguita等^[2]提出利用Grover量子搜索算法^[3]优化支持向量机SVM的训练过程用于解决SVM的训练效率问题。 Rebentrost等^[4]提出量子SVM, 利用量子计算解决训练数据的内积计算, 即利用量子计算求解矩阵的偏迹得到训练数据的归一化核矩阵。Lu等^[5]提出量子决策树算法, 利用量子态之间的保真度作为训练数据之间相似度的度量, 依此将训练集划分成子类, 并引入量子信息熵作为选择决策节点的依据建立量子决策树。阮越等^[6]提出了量子PCA算法并用于人脸识别中, 用量子态表示人脸特征, 将Grover量子搜索算法用于人脸识别的过程达到二次加速的效果。徐永振等^[7]提出基于一维三态离散量子游走的聚类算法, 将数据点看作游走粒子, 执行三态量子游走, 根据粒子的测量结果更新数据点的属性值并依此进行聚类。Elhaddad等^[8]从并行计算和优化计算两个方面分别分析了量子计算对人工智能和数据挖掘领域所带来的影响。

聚类作为一种无监督的机器学习技术, 其依据给定的相似性度量将数据划分成若干个类, 使得同一类内的数据相似度较高, 而不同类间的数据相似度较低^[9]。聚类算法被广泛应用于图像识别、社交网络、商业智能等领域中^{[10, 11]}。k-means是一种经典的聚类算法, 被誉为数据挖掘领域的十大算法之一, 自提出以来就得到了广泛的应用^{[12, 13, 14]}。然而大数据时代, 巨大的数据量为k-means聚类的速度带来了巨大的挑战, 利用基于云计算的大规模集群进行并行聚类成了较为普遍的应对策略; 但是大规模集群所产生的巨大的能量消耗问题又带来新的挑战^{[15, 16]}。而量子计算不但具有超强的并行计算能力, 又因计算的可逆性使其不会面临能量消耗的问题, 故已有学者研究利用量子计算的相关理论对k-means算法进行聚类加速。因量子态之间的信息保真度与传统相似度度量中的余弦相似度相似, Aï meur 等^[17]提出利用量子信息保真度代替k-means算法中数据之间的相似度量, 并利用受控交换门Control-Swap计算量子信息保真度, 但k-means算法的其他步骤并没有引入量子计算。随后Aï meur等^{[18, 19]}又提出了利用Grover算法的扩展算法量子最小值查找算法作为一个量子子程序去加速经典k-means算法中的一个步骤, 但算法的计算复杂度并没有降低。k-means算法对初始聚类中心的选择比较敏感, 不同的聚类中心其聚类效果可能不同, 故Lloyd等^[20]提出利用量子绝热算法选择合适的初始聚类中心点后, 再利用k-means算法进行聚类, 聚类的计算过程中并未引入量子计算。

综上所述, 有关量子计算与k-means算法相结合的工作中, 大多是利用量子计算对算法中的某一个步骤进行了加速, 但是算法整体的计算复杂度并未降低。本文给出的量子k-means算法将对聚类的主要步骤进行加速, 使算法整体计算复杂度得到降低。

1 经典k-means算法

给定数据集X= $\begin{matrix} \{x_{1}, x_{2}, \dots, x_{n}\} \end{matrix}$ , n为数据集的规模, x_i为第i个数据点, 每个数据点的特征维度为d, x_ir表示第i个数据点的第r个特征值; 数据集被划分为k个类别, 聚类中心为c= $\begin{matrix} \{c_{1}, c_{2}, \dots, c_{k}\} \end{matrix}$ 。k-means算法的聚类过程如下:

(1)随机从数据集X中选取k条记录作为初始聚类中心c。

(2)对每一数据点x_i, 计算其到k个聚类中心的相似度。

(3)将数据点x_i归于相似度最大的那个聚类中心所属的类。

(4)数据集中的所有数据经过步骤(2)(3)计算后, 根据数据集的类别标号重新计算新的聚类中心。

(5)判断是否达到聚类结束的条件, 若达到, 聚类结束; 否则回到步骤(1)。

k-means算法的主要聚类步骤和计算量集中在第(2)(3)步, 即对每个数据点计算其到k个聚类中心的相似度, 并将其归于相似度最大的聚类中心所属的类别。

2 本文算法

量子k-means算法将量子计算的相关理论引入到聚类的主要步骤, 主要分成3个阶段完成该步骤的任务:第一, 先将待聚类的数据点和k个聚类中心点制备成量子态; 第二, 利用受控交换门Control-Swap计算任一数据点x_i和k个聚类中心c= $\begin{matrix} \{c_{1}, c_{2}, \dots, c_{k}\} \end{matrix}$ 的相似度, 并利用相位估计算法将相似度存储在量子比特上; 第三, 对所求出的k个相似度利用最小值查找量子搜索算法求出最相似的聚类中心点c_j。

2.1 量子态制备

k-means算法中需要计算每一个数据点与k个聚类中心的相似度, 所以需要将其制备成量子态。量子态制备之前先将所有的数据进行归一化处理。假设任一聚类数据点x_i用具有d个特征值的向量来表示, 以待聚类的数据点x₀为例, 将数据点x₀制备成如式(1)所示的量子态:

|x₀> = $\begin{matrix} \overset{d}{\sum_{j = 1}} \end{matrix}$ |j> $\begin{matrix} (\sqrt[]{1 - x_{0 j}^{2}} | 0 > + x_{0 j} | 1 >) \end{matrix}$ |1> (1)

式中:x₀_j为第0个数据点的第j个特征值。

将k个聚类中心c= $\begin{matrix} \{c_{1}, c_{2}, \dots, c_{k}\} \end{matrix}$ 制备成如式(2)所示的量子态:

|c> = $\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ |i> $\begin{matrix} \overset{d}{\sum_{j = 1}} \end{matrix}$ |j> · $\begin{matrix} (\sqrt[]{1 - c_{ij}^{2}} | 0 > + c_{ij} | 1 >) \end{matrix}$ |1> (2)

式中:c_ij表示第i个聚类中心点的第j个特征值。

设2^m=k, 2ⁿ=d, 量子态|c> 的制备过程如下:

(1)初始输入为|0> ^m|0> ⁿ|1> |0> , 利用H门得到量子态:

$\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ |i> $\begin{matrix} \overset{d}{\sum_{j = 1}} \end{matrix}$ |j> |1> |0> (3)

(2)将量子黑箱Oracle作用到式(3)上得到:

$\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ |i> $\begin{matrix} \overset{d}{\sum_{j = 1}} \end{matrix}$ |j> |c_ij> |0> (4)

量子黑箱Oracle定义为:

|i> |j> |1> → |i> |j> |c_ij>

(3)利用一个绕Y轴旋转的酉操作R_y $\begin{matrix} (2 si n^{- 1} c_{ij}) \end{matrix}$ 作用到式(4)中的最后一个量子比特上得到:

|c> = $\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ |i> $\begin{matrix} \overset{d}{\sum_{j = 1}} \end{matrix}$ |j> |c_ij> · $\begin{matrix} (\sqrt[]{1 - c_{ij}^{2}} | 0 > + c_{ij} | 1 >) \end{matrix}$ (5)

(4)利用第(2)步的量子黑箱Oracle的逆操作清除式(5)中的|c_ij> , 得到如式(2)所示的量子态|c> 。

利用同样的方法制备如式(1)所示的量子态|x₀> 。由上述量子态的制备过程可以得到, 制备量子态|c> 需要3次Oracle操作, 制备|x₀> 与|c₀> 则需要6次Oracle操作。

2.2 相似性计算

计算量子态|x₀> 与|c> 的相似度, 并利用相位估计算法将相似度存储在量子比特中。对于相似度的计算, 仍然采用文献[17]中的方法:即采用控制交换门Control-Swap计算量子态之间的保真度用于估计相似度。

用于计算量子态|x₀> 与|c> 相似度的控制交换门Control-Swap如图1所示, 输入的第1个量子比特位经过一个H门后用作控制位, 当其为1时实现交换操作。计算的过程如下:

(1)|0> |x₀> |c> ∥ 初态。

(2)→ (|0> +|1> )|x₀> |c> ∥ 应用H门

	Figure Option View Download New Window
	图1 控制交换门Fig.1 Control-Swap gate

到第一寄存器。

(3)→ (|0> |x₀> |c> +|1> |c> |x₀> )∥执行交换操作。

(4)→ |0> (|x₀> |c> +|c> |x₀> )+|1> (|c> |x₀> -|x₀> |c> ) ∥再次应用H门。

由此得到控制交换门的输出结果为:

|ψ > =|0> (|x₀> |c> +|c> |x₀> )+|1> (|x₀> |c> -|c> |x₀> ) (6)

设测量算子M₁=|1> < 1|, 并且有M₁=|1> < 1|, 则:

p=< ψ ||ψ > =< ψ ||ψ > =

$\begin{matrix} [< 1, x_{0,} c | - < 1, c, x_{0} |] \end{matrix}$ |1> < 1|· $\begin{matrix} [| 1, x_{0,} c > - | 1, c, x_{0} >] \end{matrix}$ =

$\begin{matrix} (< x_{0,} c |-| c, x_{0} >) \end{matrix}$ · $\begin{matrix} (| x_{0,} c > - | c, x_{0} >) \end{matrix}$ =

$\begin{matrix} (2 - 2 < x_{0} | c >^{2}) \end{matrix}$ = $\begin{matrix} (1 - < x_{0} | c >^{2}) \end{matrix}$

由p可以得到第一位量子比特为1的概率为 $\begin{matrix} {(1 - < x_{0} | c >)}^{2} \end{matrix}$ , 由于量子态c是k个聚类中心点量子态c_i的叠加, 则< x₀|c> 为x₀与c_i的余弦值, 这里定义 $\begin{matrix} {(1 - < x_{0} | c >)}^{2} \end{matrix}$ 为s $\begin{matrix} (x_{0}, c_{i}) \end{matrix}$ , 用于描述x₀与c_i的相似度, 当s $\begin{matrix} (x_{0}, c_{i}) \end{matrix}$ 值越小, 其x₀与c_i的余弦值< x₀|c> 就越大, 两者就越相似。由此, 控制交换门的输出可以表示为:

φ = $\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ |i> ( $\begin{matrix} \sqrt[]{1 - s (x_{0}, c_{i})} \end{matrix}$ |0> + $\begin{matrix} \sqrt[]{s (x_{0}, c_{i})} \end{matrix}$ |1> ) (7)

接下来将相位估计算法作用在φ 上, 使相似度信息存储在量子比特上^[21]。相位估计算法用于求解给定向量的相位, 其实现原理主要是基于量子Fourier变换技术。量子Fourier主要是实现如下形式的变换:

$\begin{matrix} \overset{N - 1}{\sum_{j = 0}} \end{matrix}$ x_i|j> → $\begin{matrix} \overset{N - 1}{\sum_{k = 0}} \end{matrix}$ y_k|k> (8)

将量子态φ 作为相位估计算法的输入, 可以得到:

α = $\begin{matrix} \overset{k}{\sum_{i = 1}} \end{matrix}$ |i> | $\begin{matrix} |c_{i} - x_{0}| \end{matrix}$ > (9)

由此可将c_i与x₀之间的相似度存储于量子比特| $\begin{matrix} |c_{i} - x_{0}| \end{matrix}$ > 上, 即 $\begin{matrix} |c_{i} - x_{0}| \end{matrix}$ 越小, 两者之间的相似度越大; 同理 $\begin{matrix} |c_{i} - x_{0}| \end{matrix}$ 越大, 两者的相似度越小。由于相位估计的过程主要是Grover迭代的过程, 即需要相应的Oracle操作, 其计算量与估计的精度有关; 当精度值确定后, 其计算量则为常数, 这里假设其需要的Oracle操作的次数为R'。

2.3 相似度最大值查找

量子态α 中保存的k个 $\begin{matrix} |c_{i} - x_{0}| \end{matrix}$ 值, 可以看作是一个规模为k的无序数据库的叠加态, 其中使 $\begin{matrix} |c_{i} - x_{0}| \end{matrix}$ 达到最小的c_i便是与x₀最为相似的聚类中心, 即两者之间的相似度最大。如果利用经典查找算法查找与x₀最相似的c_i, 需要的时间复杂度为O(k)。而最小值查找量子算法作为Grover算法的一个扩展算法, 其可以O的时间复杂度从无序数据库中查找出最小值^[22]。

利用量子最小值查找算法从量子态α 中查找最小值的步骤如下:首先随机选取一个聚类中心c_j作为初始值, 然后重复以下步骤次:

(1)制备初始值c_j的量子态为β 。

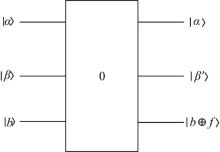
(2)α 、β 作为输入, b作为控制输入, 利用Grover算法查找到。

(3)若 $\begin{matrix} |c_{j}^{'} - x_{0}| \end{matrix}$ < $\begin{matrix} |c_{j} - x_{0}| \end{matrix}$ , 则用替换c_j并回到步骤(1)。

相应的量子搜索算法模型如图2所示。此时找到的 c_j为与x₀最近的聚类中心点, 将x₀归于c_j所属的类别。

	Figure Option View Download New Window
	图2 查找最相似的聚类中心Fig.2 Find the maximum of similarity to cluster center

3 算法复杂度分析

两种算法的时间复杂度和空间复杂度对比结果如表1所示。

表1 两种算法的复杂度比较 Table 1 Comparison of complexity of two algorithms

复杂度	经典k-means	量子k-means
时间	O	O $\begin{matrix} (tn (R + \sqrt[]{k})) \end{matrix}$
空间/bit	8(k+1)d	$\begin{matrix} (4 + 2 lo g_{2} d + lo g_{2} k) \end{matrix}$

表1 两种算法的复杂度比较 Table 1 Comparison of complexity of two algorithms

3.1 时间复杂度

经典k-means算法中的主要计算步骤为第(2)(3)步。其中第(2)步, 即对于每一个具有d个特征值的数据点x_i, 都要计算其与k个聚类中心的相似度, 该步计算的时间复杂度为O。算法第(3)步是从k个相似度中查找最大值, 其时间复杂度为O(k), 文献[23, 24]主要是对该步骤利用量子搜索算法对其加速, 使该步骤的时间复杂度降到O, 但是该步骤的加速并不会使整个算法的时间复杂度提高。对于数据规模为n需要迭代t次的聚类过程, 经典k-means算法的时间复杂度为O(tnkd)。

本文提出的量子k-means算法, 将被聚类的每一个数据点x_i与k个聚类中心制备成相应的量子叠加态, 需要的Oracle操作次数为6次。由于量子计算其内生的计算并行性, 则对于每一个数据点x_i, 利用控制交换门计算其与k个聚类中心的相似度, 只需要一步计算即可得到。得到的相似度只是作为一个中间值, 并不会对其直接测量, 而是利用相位估计算法将其存储于量子比特中, 该步的结果被直接用于查找与x_i相似度最大的聚类中心点。相位估计算法需要的Oracle操作次数为常数R', 查找最相似的聚类中心需要的时间复杂度为O。设6+R'=R, 则量子k-means算法主要步骤的计算复杂度为O, 整个量子k-means算法的时间复杂度为O $\begin{matrix} (tn (R + \sqrt[]{k})) \end{matrix}$ 。对比两种算法的时间复杂度, 可以得到:当< kd时, 即> R时, 量子k-means算法的计算速度快, 且k和d越大, 这种效果就越明显, 量子k-means算法的时间复杂度就越低。

3.2 空间复杂度

在经典k-means算法中, 对于任意数据点x_i, 假设一个特征值需要占据一个字节的内存空间, 则x_i需要的内存空间为d字节; 由于要计算其与k个聚类中心的距离, 那么其需要的内存应该为(k+1)d字节=8d比特。而对于量子k-means算法, 任一数据点x_i的量子态所需要的内存为 $\begin{matrix} (2 + lo g_{2} d) \end{matrix}$ 比特, k个聚类中心的量子态所需要的内存为 $\begin{matrix} (2 + lo g_{2} d + lo g_{2} k) \end{matrix}$ 比特, 即第一步总共需要的最大内存为 $\begin{matrix} (4 + 2 lo g_{2} d + lo g_{2} k) \end{matrix}$ 比特。对比8d和 $\begin{matrix} (4 + 2 lo g_{2} d + lo g_{2} k) \end{matrix}$ 可以看到, 量子算法的空间复杂度达到指数级降低。

4 结束语

本文在k-means算法的主要步骤中引入量子计算相关理论, 得到k-means算法的量子化版本。首先给出了任一聚类数据x_i和k个聚类中心的量子态制备过程, 然后给出了x_i和这k个聚类中心距离的相似度计算过程, 并利用相位估计算法将相似度转换成量子比特, 最后, 利用最小值查找量子算法查找出最相似的聚类中心点并将其归于所属的类别。对两种算法的时间复杂度进行理论分析和比较可以得到, 在k和d比较大的情况下, 量子k-means算法相对经典算法的时间复杂度得到降低, 且k和d越大, 这种效果越明显; 而量子k-means的空间复杂度相对经典算法则可以达到指数级降低。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王书浩, 龙桂鲁. 大数据与量子计算[J]. 科学通报, 2015, 60(5): 499-508. Wang Shu-hao, Long Gui-lu. Big data and quantum computation[J]. Chin Sci Bull, 2015, 60(5): 499-508. [本文引用:1]
[2]	Anguita D, Ridella S, Rivieccio F, et al. Quantum optimization for training support vector machines[J]. Neural Networks, 2003, 16(5/6): 763-770. [本文引用:1]
[3]	Grover L K. A fast quantum mechanical algorithm for database search[C] ∥Proc 28th Ann ACM Symp Theory of Computing, New York, USA, 1996: 212-219. [本文引用:1]
[4]	Rebentrost P, Mohseni M, Lloyd S. Quantum support vector machine for big data classification[J]. Physical Review Letters, 2014, 113(13): 130503. [本文引用:1]
[5]	Lu S, Braunstein S L. Quantum decision tree classifier[J]. Quantum Information Processing, 2014, 13(3): 757-770. [本文引用:1]
[6]	阮越, 陈汉武, 刘志昊, 等. 量子主成分分析算法[J]. 计算机学报, 2014, 37(3): 666-676. Ruan Yue, Chen Han-wu, Liu Zhi-hao, et al. Quantum principal component analysis algorithm[J]. Chinese Journal of Computers, 2014, 37(3): 666-676. [本文引用:1]
[7]	徐永振, 郭躬德, 蔡彬彬, 等. 基于一维三态量子游走的量子聚类算法[J]. 计算机科学, 2016, 43(3): 80-83. Xu Yong-zhen, Guo Gong-de, Cai Bin-bin, et al. Quantum clustering algorithm based on one-dimensional three-state quantum walk[J]. Computer Science, 2016, 43(3): 80-83. [本文引用:1]
[8]	Elhaddad M E, Mohammed S A O. Analysing the impact of quantum computing using system dynamics[C]∥Engineering & MIS (ICEMIS), IEEE, 2016: 1-5. [本文引用:1]
[9]	Jain A K, Murty M N, Flynn P J. Data clustering: a review[J]. ACM Computing Surveys (CSUR), 1999, 31(3): 264-323. [本文引用:1]
[10]	许美慧, 尹建芹, 张玲, 等. 可处理暗腔的日冕物质抛射检测新方法[J]. 光学精密工程, 2016, 24(10s): 591-599. Xu Mei-hui, Yin Jian-qin, Zhang Ling, et al. New detection method for coronal mass ejection capable of dark cavity processing[J]. Optics and Precision Engineering, 2016, 24(10s): 591-599. [本文引用:1]
[11]	王丽. 融合底层和中层字典特征的行人重识别[J]. 中国光学, 2016, 9(5): 540-546. Wang Li. Pedestrian re-identification based on fusing low-level and mid-level features[J]. Chinese Optics, 2016, 9(5): 540-546. [本文引用:1]
[12]	Wu X, Kumar V, Quinlan J R, et al. Top 10 algorithms in data mining[J]. Knowledge and Information Systems, 2008, 14(1): 1-37. [本文引用:1]
[13]	秦大同, 詹森, 漆正刚, 等. 基于 K-均值聚类算法的行驶工况构建方法[J]. 吉林大学学报: 工学版, 2016, 46(2): 383-389. Qin Da-tong, Zhan Sen, Qi Zheng-gang, et al. Driving cycle construction using K-means clustering method[J]. Journal of Jilin University(Engineering and Technology Edition), 2016 , 46(2): 383-389. [本文引用:1]
[14]	赵文昌, 李忠木. 融合改进人工蜂群和K均值聚类的图像分割[J]. 液晶与显示, 2017, 32(9): 726-735. Zhao Wen-chang, Li Zhong-mu. Image segmentation algorithm based on improved artificial bee colony and K-mean clustering[J]. Chinese Journal of Liquid Crystals and Displays, 2017, 32(9): 726-735. [本文引用:1]
[15]	丁有伟, 秦小麟, 刘亮, 等. 一种异构集群中能量高效的大数据处理算法[J]. 计算机研究与发展, 2015, 52(2): 377-390. Ding You-wei, Qin Xiao-lin, Liu Liang, et al. An energy efficient algorithm for big data processing in heterogeneous cluster[J]. Journal of Computer Research and Development, 2015, 52(2): 377-390. [本文引用:1]
[16]	Forrest W. How to cut datacentre carbon emissions?[EB/OL]. [2014-12-08]. http//www.computerweekly.com/Articles/2008/12/05/233748/how-tocut-data-centrecarbon-emissions.htm [本文引用:1]
[17]	Aïmeur E, Brassard G, Gambs S. Machine learning in a quantum world[J]. Advances in Artificial Intelligence, 2006, 4013: 431-442. [本文引用:1]
[18]	Aïmeur E, Brassard G, Gambs S. Quantum clustering algorithms[C]∥Proceedings of the 24th International Conference on Machine Learning, 2007: 1-8. [本文引用:1]
[19]	Aïmeur E, Brassard G, Gambs S. Quantum speed-up for unsupervised learning[J]. Machine Learning, 2013, 90(2): 261-287. [本文引用:1]
[20]	Lloyd S, Mohseni M, Rebentrost P. Quantum algorithms for supervised and unsupervised machine learning[J]. arXiv, 2013: 1307. 0411. [本文引用:1]
[21]	Brassard G, Hoyer P, Mosca M, et al. Quantum amplitude amplification and estimation[J]. Contemporary Mathematics, 2002, 305: 53-74. [本文引用:1]
[22]	Durr C, Hoyer P. A quantum algorithm for finding the minimum[J/OL]. [2016-07-11]. https://arxiv.org/abs/quant-ph/9607014. [本文引用:1]
[23]	李强, 蒋静坪. 量子K最近邻算法[J]. 系统工程与电子技术, 2008, 30(5): 940-943. Li Qiang, Jiang Jing-ping. Quantum K nearest neighbor algorithm[J]. Systems Engineering and Electronics, 2008, 30(5): 940-943. [本文引用:1]
[24]	陈汉武, 高越, 张军. 量子K-近邻算法[J]. 东南大学学报: 自然科学版, 2015, 45(4): 647-651. Chen Han-wu, Gao Yue, Zhang Jun. Quantum K-nearest neighbor algorithm[J]. Journal of Southeast University(Natural Science Edition), 2015, 45(4): 647-651. [本文引用:1]

2015

0.0

. 2015, 60(5):499-508

Big data and quantum computation

大数据与量子计算

Wang Shu-hao , Long Gui-lu.

王书浩, 龙桂鲁

... 0 引言近年来,越多越多的学者将量子计算应用于数据挖掘领域^[1] ...

2003

0.0

... Anguita等^[2]提出利用Grover量子搜索算法^[3]优化支持向量机SVM的训练过程用于解决SVM的训练效率问题 ...

1996

0.0

... Anguita等^[2]提出利用Grover量子搜索算法^[3]优化支持向量机SVM的训练过程用于解决SVM的训练效率问题 ...

2014

0.0

... Rebentrost等^[4]提出量子SVM,利用量子计算解决训练数据的内积计算,即利用量子计算求解矩阵的偏迹得到训练数据的归一化核矩阵 ...

2014

0.0

... Lu等^[5]提出量子决策树算法,利用量子态之间的保真度作为训练数据之间相似度的度量,依此将训练集划分成子类,并引入量子信息熵作为选择决策节点的依据建立量子决策树 ...

2014

0.0

. 2014, 37(3):666-676 DOI:doi:10.3724/SP.J.1016.2014.00666

Quantum principal component analysis algorithm

量子主成分分析算法

Ruan Yue , Chen Han-wu , Liu Zhi-hao

阮越, 陈汉武, 刘志昊

主成分分析(Principal Component Analysis,PCA)是模式识别领域,尤其是人脸识别中一种应用广泛的重要算法.然而,在此算法及其后续的改造算法中始终存在两个主要问题:(1)降维处理后的特征空间依然较大;(2)用于比较两幅人脸特征相似性的测度方法计算量较大,从而导致算法在识别阶段的时间效率较差.该文基于量子信息的相关理论与方法,并受算术编码基本思想的启发,提出了量子PCA算法.设计了一种人脸特征编码方案,进一步压缩了降维处理后的特征空间;将两幅人脸特征的相似性测度方法改为在某一阈值条件下的等值判定;应用Grover算法修改识别阶段的处理流程,使得算法的时间效率有了显著提高.

... 阮越等^[6]提出了量子PCA算法并用于人脸识别中,用量子态表示人脸特征,将Grover量子搜索算法用于人脸识别的过程达到二次加速的效果 ...

2016

0.0

. 2016, 43(3):80-83 DOI:doi:10.11896/j.issn.1002-137X.2016.3.016

Quantum clustering algorithm based on one-dimensional three-state quantum walk

基于一维三态量子游走的量子聚类算法

Xu Yong-zhen , Guo Gong-de , Cai Bin-bin

徐永振, 郭躬德, 蔡彬彬

量子游走具有与经典随机游走不同的特性,因此它已经被用来解决包括元素区分、组合优化、图同构等问题.考虑量子游走和聚类两个领域,提出了一个基于一维三态离散量子游走的聚类算法.在该算法中,将数据点看作游走粒子;然后,这些粒子执行三态量子游走,接着根据粒子的测量结果更新数据点的属性值;最后,属于同一簇的数据点将会聚集,而属于不同簇的数据点将会分离.仿真实验结果表明了所提算法的有效性.

... 徐永振等^[7]提出基于一维三态离散量子游走的聚类算法, 将数据点看作游走粒子,执行三态量子游走,根据粒子的测量结果更新数据点的属性值并依此进行聚类 ...

2016

0.0

... Elhaddad等^[8]从并行计算和优化计算两个方面分别分析了量子计算对人工智能和数据挖掘领域所带来的影响 ...

1999

0.0

... 聚类作为一种无监督的机器学习技术,其依据给定的相似性度量将数据划分成若干个类,使得同一类内的数据相似度较高,而不同类间的数据相似度较低^[9] ...

2016

0.0

. 2016, 24(10s):591-599

New detection method for coronal mass ejection capable of dark cavity processing

可处理暗腔的日冕物质抛射检测新方法

Xu Mei-hui , Yin Jian-qin , Zhang Ling

许美慧, 尹建芹, 张玲

为了有效识别在大角度光谱日冕仪图像中的日冕物质抛射（Coronal Mass Ejections，CMEs），提出了一种基于的可以有效处理暗腔的识别方法。首先采用中值滤波进行预处理去除噪声，然后采用均值聚类算法对差分图像进行初步分类，统计分类后各类别的分布特性，利用该分布特性识别一级分类，成功识别出明显的高亮CME图像和暗腔CME图像；接着采用二次聚类方法，对于识别成无CME的日冕仪图像采用分块策略和极坐标转换算法，然后对其继续均值聚类，并对二次聚类结果进行统计，利用分布特性完成二级分类。实验结果表明，该算法能从拍摄的日冕仪图像中较有效地检测出CME图像，并能在图像中直接标明和显示出CME区域点，尤其对带暗腔的CME有较好的效果。对于高亮CME给出的具体测量阈值是第三类类心灰度值为200~250，对于暗腔CME给出的具体测量阈值是第一类类心灰度值在120以下，且类内像素点在1000~30000之间。

... 聚类算法被广泛应用于图像识别、社交网络、商业智能等领域中^[10,11] ...

2016

0.0

. 2016, 9(5):540-546

Pedestrian re-identification based on fusing low-level and mid-level features

融合底层和中层字典特征的行人重识别

Wang Li.

王丽

... 聚类算法被广泛应用于图像识别、社交网络、商业智能等领域中^[10,11] ...

2008

0.0

... k-means是一种经典的聚类算法,被誉为数据挖掘领域的十大算法之一,自提出以来就得到了广泛的应用^[12,13,14] ...

2016

0.0

. 2016, 46(2):383-389 DOI:doi:10.13229/j.cnki.jdxbgxb201602008

Driving cycle construction using K-means clustering method

K-均值聚类算法的行驶工况构建方法

Qin Da-tong , Zhan Sen , Qi Zheng-gang

秦大同, 詹森, 漆正刚, . 基于

摘　要：提出一种基于K-均值聚类算法的城市循环工况构建方法,该方法通过实车采集某城市道路行驶工况的数据,将工况数据预处理后划分为工况块,运用平均速度、行驶距离和巡航时间比3个参数对工况块进行K-均值聚类分析,采用距离聚类中心越近越能代表簇特征的原则选取工况块,最终拟合出某城市循环工况,并对其从特征参数、转毂实验和废气分析采集的油耗和排放数据3个方面与其他典型城市循环工况进行了对比。对比分析结果表明：采用本方法构建的城市循环工况能够很好地反映某地实际交通道路状况,具有实用价值。

... k-means是一种经典的聚类算法,被誉为数据挖掘领域的十大算法之一,自提出以来就得到了广泛的应用^[12,13,14] ...

2017

0.0

. 2017, 32(9):726-735 DOI:doi:10.3788/YJYXS20173209.0726

Image segmentation algorithm based on improved artificial bee colony and K-mean clustering

融合改进人工蜂群和K均值聚类的图像分割

Zhao Wen-chang , Li Zhong-mu.

赵文昌, 李忠木

摘　要：针对人工蜂群优化的K均值算法易陷入局部最优、搜索精度不够、分割图像不够细致等问题,本文融合自适应人工蜂群和K均值聚类,提出了一种新的图像分割算法。算法首先利用距离最大最小乘积对种群进行初始化;其次采用自适应搜索参数动态调整邻域搜索范围,使人工蜂群算法快速收敛于全局最优;然后将人工蜂群输出的所有蜜源进行K均值聚类,克服K均值聚类结果对初始聚类中心的依赖,再将聚类划分结果进行Powell局部搜索,加快算法收敛的速度,将得到的新聚类中心更新蜂群中蜜源位置。最后,将本文算法与其他两种同类分割算法进行试验对比。实验结果表明：与其他两种算法相比,本文提出的分割算法在保证运行时间的前提下,分割准确率比其他两种算法分别至少提高了3.5%和4.8%,表现出了较高的分割质量。

... k-means是一种经典的聚类算法,被誉为数据挖掘领域的十大算法之一,自提出以来就得到了广泛的应用^[12,13,14] ...

2015

0.0

. 2015, 52(2):377-390 DOI:doi:10.7544/issn.1000-1239.2015.20140126

An energy efficient algorithm for big data processing in heterogeneous cluster

一种异构集群中能量高效的大数据处理算法

Ding You-wei , Qin Xiao-lin , Liu Liang

丁有伟, 秦小麟, 刘亮

It is reported that the electricity cost to operate a cluster may well exceed its acquisition cost, and the processing of big data requires large scale cluster and long period. Therefore, energy efficient processing of big data is essential for the data owners and users, and it is also a great challenge for the energy use and environment protection. Existing methods powered down some nodes to reduce energy consumption or developed new strategies of data storage in the cluster. However, we can find that much energy is still wasted even minimal nodes are used to process the task, and new storage strategies do not suit for the deployed clusters for the extra cost of data transformation. In this paper, we propose a novel algorithm MinBalance to processing I/O intensive big data tasks energy efficiently in heterogeneous cluster. The algorithm can be divided into two steps, node selection and workload balance. In the former step, four greedy policies are used to select the proper nodes considering heterogeneity of the cluster. While in the latter step, the workloads of the selected nodes will be well balanced to avoid the energy wastes caused by waiting. MinBalance is a universal algorithm and cannot be affected by the data storage strategies. Experimental results indicate that MinBalance can achieve over 60% energy reduction for large data sets over the traditional methods of powering down partial nodes.

集群的能量消耗已经超过了其本身的硬件购置费用，而大数据处理需要大规模的集群耗费大量时间，因此如何进行能量高效的大数据处理是数据拥有者和使用者亟待解决的问题，也是对能源和环境的一个巨大挑战.现有的研究一般通过关闭部分节点以减少能量消耗，或者设计新的数据存储策略以便实施能量高效的数据处理.通过分析发现即便使用最少的节点也存在很大的能源浪费，而新的数据存储策略对于已经部署好的集群会造成大规模的数据迁移，消耗额外的能量.针对异构集群下I/O密集型的大数据处理任务，提出一种新的能量高效算法MinBalance，将问题分为节点选择和负载均衡两个步骤.在节点选择阶段采用4种不同的贪心策略，充分考虑到节点的异构性，尽量选择最合适的节点进行任务处理；在负载均衡阶段对选择的节点进行负载均衡，以减少各个节点因为等待而造成的能量浪费.该方法具有通用性，不受数据存储策略的影响.实验表明MinBalance方法在数据集较大的情况下相对于传统关闭部分节点的方法可以减少超过60%的能量消耗.

... 但是大规模集群所产生的巨大的能量消耗问题又带来新的挑战^[15,16] ...

0.0

... 但是大规模集群所产生的巨大的能量消耗问题又带来新的挑战^[15,16] ...

2006

0.0

... meur 等^[17]提出利用量子信息保真度代替k-means算法中数据之间的相似度量,并利用受控交换门Control-Swap计算量子信息保真度,但k-means算法的其他步骤并没有引入量子计算 ...

2007

0.0

... meur等^[18,19]又提出了利用Grover算法的扩展算法量子最小值查找算法作为一个量子子程序去加速经典k-means算法中的一个步骤,但算法的计算复杂度并没有降低 ...

2013

0.0

2013

0.0

... k-means算法对初始聚类中心的选择比较敏感,不同的聚类中心其聚类效果可能不同,故Lloyd等^[20]提出利用量子绝热算法选择合适的初始聚类中心点后,再利用k-means算法进行聚类,聚类的计算过程中并未引入量子计算 ...

2002

0.0

... 上,使相似度信息存储在量子比特上^[21] ...

0.0

... 而最小值查找量子算法作为Grover算法的一个扩展算法,其可以O的时间复杂度从无序数据库中查找出最小值^[22] ...

2008

0.0

. 2008, 30(5):940-943 DOI:doi:10.3321/j.issn:1001-506X.2008.05.040

Quantum K nearest neighbor algorithm

量子K最近邻算法

Li Qiang , Jiang Jing-ping.

李强, 蒋静坪

为减少经典K最近邻算法的时间复杂度,提出了量子K最近邻算法(QKNN).介绍了QKNN算法的构造步骤,然后为减少量子计数子程序的运行时间,进一步将固定的K值修改为可变的k,形成改进的k可变的量子最近邻算法(QkvNN).为弥补由于最近邻个数K变化带来的分类错误率上升的影响,在Boosting算法框架下,用三个由QkvNN算法训练的弱分类器,去构造了一个强分类器,从而提高单独运行QkvNN的分类精度.在此算法中,由于利用了量子计算的强大能力.使得经典K最近邻算法的时间复杂度从O(N)减小为O(平方根N).

2015

0.0