面向对象软件系统演化模型

引用本文

马健, 樊建平, 刘峰, 李红辉. 面向对象软件系统演化模型. 2018, 48(2): 545-550
MA Jian, FAN Jian-ping, LIU Feng, LI Hong-hui. The evolution model of objective-oriented software system. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 545-550 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161293
Permissions

面向对象软件系统演化模型

马健¹, 樊建平², 刘峰¹, 李红辉¹

1.北京交通大学计算机与信息技术学院,北京 100044

2.中国科学院深圳先进技术研究院,广东深圳 518055

作者简介:马健(1985-),女,博士研究生.研究方向:复杂网络. E-mail:13112083@bjtu.edu.cn

基金项目:“863”国家高技术研究发展计划项目(2015AA043701)

摘要

提出了一种基于局域事件的软件网络演化模型,该模型以面向对象软件系统为研究对象,对BA无标度网络模型进行改进,增加了添加节点、添加边、删除边和边的重连等局域事件,模拟软件网络的演化过程。实验结果表明,该模型演化生成网络的度分布服从衰减幂律分布,模型能较好地描述真实软件的演化增长情况,并且与真实软件网络的度分布基本一致,仿真实验验证了该模型的有效性。同时,该模型可以对面向对象软件网络结构进行模拟和评价。

关键词: 计算机软件; 软件演化; 无标度网络; 度分布; 复杂网络

中图分类号:TP311 文献标志码:A 文章编号:1671-5497(2018)02-0545-06

The evolution model of objective-oriented software system

MA Jian¹, FAN Jian-ping², LIU Feng¹, LI Hong-hui¹

1.School of Computer Science and Information Technology, Beijing Jiaotong University, Beijing 100044, China

2.Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China

Abstract

An evolution model of software networks based on local events is proposed. The model uses objective-oriented software systems as research object and improves the BA scale-free network model. By adding local events, such as addition of nodes, addition of edges, removal of edges and rewriting edges, the proposed model simulates the evolution of software networks. Simulation results show that the degree distribution of the network generated by this model follows power law distribution. The model can simulate the evolution process of real software, and the degree distribution is in agreement with that of real software network, which validates the proposed model. Meanwhile, the proposed model can simulate and evaluate the structures of object-oriented software networks.

Key words: computer software; software evolution; scale-free network; degree distribution; complex network

Show Figures

0 引言

自然界和人类社会中的大量系统都可以通过复杂网络加以描述^[1]。面向对象软件系统也可以转化为人工复杂网络。这方面的研究有:Bhattacharya等^[2]分析了软件源代码, 将函数抽象为节点, 调用关系抽象为有向边构造图形, 生成软件拓扑结构。Chong等^[3]不仅构造了软件图形, 还为边分配权重进行了扩展。Chaikalis等^[4]将类抽象为节点, 将类之间的(调用、关联、依赖)关系抽象为有向边。Turnu等^[5]分析了Java、Eclipse和Netbeans大型面向对象软件系统的源代码, 研究了源代码中的类和它们之间的依赖关系和整个发行版及其子项目的复杂性, 结果表明, 这样的系统可以被看作是复杂软件网络。

网络演化是网络的结构发生变化, 网络演化的模型有:Barabá si等^[6]提出了BA无标度网络模型, 模型基于增量增长和线性优先关系两种机制; Valverde等^[7]提出了基于节点复制和边重新连接的模型; Myers^[8]提出了基于重构过程的模型。Dorogovtsev等^[9]提出了依赖现有节点的度数和年龄的模型; Zheng等^[10]也提出了一个基于节点的度数和年龄的模型(Degree and age dependent adjustable evolution, DAAE); Li等^[11]提出了一种模拟软件网络演化的模块连接机制, 使用模块化连接代替在前面的模型中采用的单节点连接, 因为将面向对象系统模块化与现实世界软件本质上更加相似。张锡哲等^[12]提出一种新颖的基于复杂网络的服务软件行为演化模型, 在大量真实服务数据的基础上, 考察了面向服务的软件系统的演化仿真并分析其拓扑特征, 与传统软件所构成的软件网络进行了对比, 指出面向服务的软件系统特有的特征规律。还有一些模型也从不同的角度模拟了软件网络演化这一过程^[13]。

本文提出了一种基于局域事件(Local events)的软件网络演化模型, 模型以面向对象软件系统为研究对象, 分析软件系统网络的度分布, 模拟软件网络的演化过程。

1 基本概念

1.1 软件网络

本文中从软件的源代码中提取组成系统的类抽象为节点, 它们之间的关系抽象为边, 例如:源类引用目标类对象, 将目标类对象作为局部变量或者源类方法的参数或返回类型是目标类。软件系统转化为由许多相互连接的类组成的类图。这样, 复杂的软件系统就用软件类图表示, 研究结论表明像大量人工网络那样, 软件类图也具有“ 小世界” 和“ 无标度” 的特性^[14]。我们将类图看作软件网络, 也就是将面向对象软件系统也可以转化为人工网络。

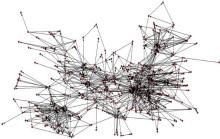
图1为Junit软件类图。将类抽象为节点, 类之间的关系抽象为边, Junit软件类图可以看作是错综复杂的软件网络。

	Figure Option View Download New Window
	图1 Junit 软件类图Fig.1 Junit class diagrams

度分布是网络统计性质中最重要的性质, 也称为网络节点的度分布, 分布情况可用分布函数P(k)表示, P(k)表示一个随机选定的节点的度恰好为k的概率。网络中一个节点直接连接的邻接点的多少通常反映了它在网络中的重要程度。例如万维网、电影演员网、论文引用关系网等, 新演员总是愿意与有影响力的演员合作, 网页链接总是更多地指向那些有很多连接指向它的网页, 一篇论文被引用的次数越多, 被新论文引用的概率就越大。

1.2 BA无标度网络模型 (Scale-free networks)

1999年, Barabá si等^[15]提出了无标度网络(Scale-free networks)模型, 具有幂律分布的网络被称为无标度网络, 其度分布具有胖尾现象, 实验结果表明许多现实的大规模网络的度分布服从幂律分布。

BA网络包括两个特性:

(1)增长。初始时具有少量m₀个节点, 每个时间步增加一个新节点, 连接到m $\begin{matrix} (m \leq m_{0}) \end{matrix}$ 个已存在于系统中的旧节点上。

(2)优先连接。新节点连接到旧节点的概率与旧节点的度成正比, N表示网络节点总数。

∏ (k_i)=k_i $\begin{matrix} / \overset{N}{\sum_{j = 1}} k_{j} \end{matrix}$ (1)

经过t时间间隔后, 网络演化为一个有N=m₀+mt个节点、mt条边的网络, 达到稳定的状态。

P(k)= $\begin{matrix} \frac{2 m (m + 1)}{k (k + 1) (k + 2)} \end{matrix}$ ∝ 2m²k^-³(2)

无标度网络模型是节点的度连接没有明显的特征长度, 因此也称为无标度网络。该模型描述了网络具有演化生长和节点依附偏好的特性, 即精确或近似地遵循幂函数的度分布。

2 基于局域事件网络演化模型

软件最初的版本一般都相对简单, 软件内部的复杂程度也相对一般, 但随着时间的推移, 为满足新的需求或加入新的功能会对程序进行修改, 软件的复杂程度也会不断地增加。在真实的软件系统中, 新增类加入到软件中与软件中已存在的类发生关系, 已存在的类之间也会改变现有的各种关系或删除已存在的类及其关系。局域事件演化网络模型模拟了上述情形, 例如:带有新边的新节点与现有节点之间的连接, 在网络中现有节点间添加新边, 现有边的删除和重新连接。在BA模型的基础上, 本文提出了基于局域事件网络演化模型模拟真实软件网络的演化过程。

(1)初始网络:具有少量m₀个节点。

(2)网络演化:

①以概率p₁增加一个新节点, 新节点连接m条新边, 新节点按择优概率式(1)选取节点i与新增节点产生一条边, 这个过程重复m次。

$\begin{matrix} (\frac{\partial k_{i}}{\partial t}) \end{matrix}$ =p₁m+p₁m $\begin{matrix} \frac{k_{i}}{\sum_{j} k_{j}} \end{matrix}$ (3)

②以概率p₂在网络已有节点之间增添m条边, 新增的边一端按择优概率公式(1)∏ 选取节点i, 另一个节点也按择优概率公式(1)∏ (k_j)选取节点j。

$\begin{matrix} (\frac{\partial k_{i}}{\partial t}) \end{matrix}$ =p₂m $\begin{matrix} (\frac{k_{i}}{\sum_{j} k_{j}} + \frac{k_{i}}{\sum_{j} k_{j}}) \end{matrix}$ (4)

③以概率p₃在网络已有节点之间删除m条边。

$\begin{matrix} (\frac{\partial k_{i}}{\partial t}) \end{matrix}$ =-p₃m(5)

综合上述3种情况, 将式(3)(4)(5)相加可得:

$\begin{matrix} \frac{\partial k_{i}}{\partial x} \end{matrix}$ =(p₁-p₃)m+(p₁+2p₂)m $\begin{matrix} \frac{k_{i}}{\sum_{j} k_{j}} \end{matrix}$ (6)

式中:N=m₀+mt; ∑ _jk_j=2mt-m; 对于较大的t、m₀和m可以忽略, 初始条件t_i时刻增加的连接数为m, k_i(t_i)=m。

对上述微分方程(6)求解得:

k_i=m $\begin{matrix} {(\frac{t}{t_{i}})}^{γ} \end{matrix}$ , γ = $\begin{matrix} \frac{p_{1} + 2 p_{2}}{2} \end{matrix}$

网络中所有的节点都以同样的幂律增长, γ 称为动力学指数。p₁+p₂+p₃=1。

随机变量t_i服从(0, t)区间上的均匀分布, 有:p_i(t)= $\begin{matrix} \frac{1}{m_{0} + t} \end{matrix}$ ;

P $\begin{matrix} \{k_{i} (t) < k\} \end{matrix}$ =1- $\begin{matrix} \frac{m^{\frac{1}{γ}} t}{k^{\frac{1}{γ}} (m_{0} + t)} \end{matrix}$ ;

P(k, t)= $\begin{matrix} \frac{\partial P \{k_{i} (t) < k\}}{\partial k} \end{matrix}$ = $\begin{matrix} \frac{\frac{1}{γ} m^{\frac{1}{γ}} t}{m_{0} + t} \end{matrix} \begin{matrix} \frac{1}{k^{\frac{1}{γ}} + 1} \end{matrix}$ 。

当t→ ¥ 时, 有

P(k)= $\begin{matrix} \lim_{t \to \infty} \end{matrix}$ P(k, t)∝ $\begin{matrix} m^{\frac{1}{γ}} \end{matrix} \begin{matrix} k^{- \frac{1}{γ} - 1} \end{matrix}$ = $\begin{matrix} \frac{2}{p_{1} + 2 p_{2}} \end{matrix} \begin{matrix} m^{\frac{2}{(p_{1} + 2 p_{2})}} \end{matrix} \begin{matrix} k^{- \frac{2}{(p_{1} + 2 p_{2})} - 1} \end{matrix}$ (7)

由式(7)可以看出, 基于局域事件网络演化模型也是无标度模型。

3 实验分析

3.1 实验数据

Dependency Finder分析工具可以实现从Java字节码文件中抽取面向对象软件类关系和度量。在本实验中使用Dependency Finder抽取所选实验对象类的之间关系进行分析。

为验证本文提出的基于局域事件的无标度网络模型, 选取了6款Java面向对象开源软件, 表1为Azureus5.7.1.0, structs1.3.10, tomcat9.0.0, ant1.9.7, itext5.5.9, jedit4.3的参数, 使用Mablab对生成的幂律函数曲线进行分析拟合。

表1 软件相关参数 Table 1 Software related parameters

3.2 实验结果分析

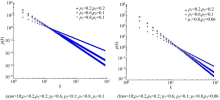
图2为在双对数坐标中的参数分析, 是提出的模型式(7)的度分布曲线。对变量分别取对数可以得到度分布曲线是一条负斜率的直线, 所以, 得到模型为无标度网络模型。

	Figure Option View Download New Window
	图2 模型不同参数度分布图Fig.2 Different parameter of model degree distribution

本文分析了6个面向对象软件系统, 以Azureus5.7.1.0为例, 图3(a)中的‘ * ’ 为Azureus真实网络的度分布, ‘ +’ 为BA无标度网络模型的度分布曲线, ‘ ∙ ’ 为基于局域事件(LE)的无标度网络的度分布曲线。可以看出, 在图3(a)的双对数坐标中, Azureus真实网络度分布具有胖尾现象。说明度数大的节点占少数, 大部分的节点的度数较小, 度数较大的少数节点对应于软件系统中的通用类, 这些类被程序员经常使用。上述结果表明, 面向对象软件系统的度分布遵循幂律分布。

这种基于局域网络演化机制的模型适合描述面向对象软件系统, 软件网络经过长时间演化后, 导致网络中大多数节点拥有少数连接的边, 而极少数节点, 拥有大量连接。结果导致“ 富者越富” 和中枢点现象。这些软件网络的度分布都服从幂律分布。

采用目前通用的验证度指数的方法, 根据初步统计, 对软件系统进行度指数分析。所有软件网络拟合后曲线的斜率均在区间, 结论与建模分析得到的结论一致。显然, 本文提出的模型更能较好地模拟真实网络的度分布情况, 模拟Azureus仿真网络的参数为m=10, p₁=0.8, p₂=0.1; 模拟structs仿真网络的参数为m=10, p₁=0.8, p₂=0.06; 其他模拟仿真网络的参数如表2所示, 与实际系统的演化度分布情况基本一致。

	Figure Option View Download New Window
	图3 软件系统演化模型的仿真结果Fig.3 Simulation results of software systems

表2 模拟参数 Table 2 Simulation parameters

综上所述, 软件系统经过长时间演化后, 导致网络中大多数节点拥有少数连接的边, 而极少数节点, 拥有大量连接。即软件大多数节点较少与其他节点产生依赖(调用、继承、消息等)关系, 极少节点与大量其他节点具有依赖关系。例如:有的工具类被许多其他类调用, 面向对象软件网络具有复杂网络特性, 即度分布服从幂律分布。

4 结束语

本文选取了6款开源面向对象软件系统为研究对象, 对BA无标度网络模型进行改进, 增加了添加节点、添加边、删除边和边的重连等局域事件, 模拟软件网络的演化过程。实验结果表明, 软件系统的度分布服从衰减幂律分布和无标度分布。标度指数在2和3之间, 也就是说, 大规模软件系统的度分布服从衰减幂律分布的无标度分布, 这种现象说明通用类在软件系统的成长过程中发挥着重要作用, 其中代码重用引起了“ 富者越富” 现象的产生。软件演化的过程中还伴随着节点和边的添加、移除和边的重连现象, 为了描述软件系统的演化过程, 构建了一个软件系统演化模型, 模拟软件网络演化增长, 就是文中提出的基于局域事件的网络演化模型。实验结果表明, 该模型的度分布与实际软件网络基本相符, 提出的模型能较好地描述真实软件的演化增长情况, 计算得到的幂律指数与真实软件的度分布基本一致。数据仿真验证了该模型的有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	郭玉泉, 李雄飞. 复杂网络社区的分形聚类检测方法[J]. 吉林大学学报: 工学版, 2016, 46(5): 1633-1638. Guo Yu-quan, Li Xiong-fei. Fractal clustering method for uncovering community of complex network[J]. Journal of Jinlin University(Engineering and Technology Edition), 2016, 46(5): 1633-1638. [本文引用:1]
[2]	Bhattacharya P, Iliofotou M, Neamtiu I, et al. Graph-based analysis and prediction for software evolution[C]∥Proceedings of the 34th International Conference on Software Engineering(ICSE). Zuricah: ACM, 2012: 419-429. [本文引用:1]
[3]	Chong C Y, Lee S P. Analyzing maintainability and reliability of object-oriented software using weighted complex network[J]. Journal of Systems and Software, 2015, 110: 28-53. [本文引用:1]
[4]	Chaikalis T, Chatzigeorgiou A. Forecasting java software evolution trends employing network models[J]. IEEE Transactions on Software Engineering, 2015, 41(6): 582-602. [本文引用:1]
[5]	Turnu I, Concas G, Marchesi M, et al. The fractal dimension of software networks as a global quality metric[J]. Information Sciences, 2013, 245(10): 290-303. [本文引用:1]
[6]	Barabási A L, Albert R. Emergence of scaling in rand om networks[J]. Science, 1999, 286(5439): 509-512. [本文引用:1]
[7]	alverde S, Solé R V. Network motifs in computational graphs: a case study in software architecture[J]. Physical Review E Statistical Nonlinear and Soft Matter Physics, 2005, 72(2): 026107. [本文引用:1]
[8]	Myers C R. Software systems as complex networks: structure, function, and evolvability of software collaboration graphs[J]. Physical Review E Statistical Nonlinear and Soft Matter Physics, 2003, 68(2): 046116. [本文引用:1]
[9]	Dorogovtsev S N, Mendes J F F. Evolution of reference networks with aging[J]. Physical Review E Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics, 2000, 62(2): 1842-1845. [本文引用:1]
[10]	Zheng X L, Zeng D, Li H, et al. Analyzing open-source software systems as complex networks[J]. Physica A Statistical Mechanics and Its Applications, 2008, 387(24): 6190-6200. [本文引用:1]
[11]	Li H, Zhao H, Cai W, et al. A modular attachment mechanism for software network evolution[J]. Physica A Statistical Mechanics and Its Applications, 2013, 392(9): 2025-2037. [本文引用:1]
[12]	张锡哲, 吕天阳, 张斌. 基于服务交互行为的复杂服务协同网络建模[J]. 软件学报, 2016, 27(2): 231-246. Zhang Xi-zhe, Lü Tian-yang, Zhang Bin. Modeling complex collaboration network for service-oriented software based on execution behaviors[J]. Journal of Software, 2016, 27(2): 231-246. [本文引用:1]
[13]	Dabrowski R, Stencel K, Timoszuk G. Software is a directed multigraph[C]∥Proceedings of the 5th European conference on Software architecture. Essen: Spring, 2011: 360-369. [本文引用:1]
[14]	Valverde S, Cancho R F I, Sole R V. Scale-free networks from optimal design[J]. Europhysics Letters, 2002, 60(4): 512-517. [本文引用:1]
[15]	Barabási A L, Alert R, Jeong H. Mean-field theory for scale-free rand om networks[J]. Physica A Statistical Mechanics and Its Applications, 1999, 272(1): 173-187. [本文引用:1]

2016

0.0

. 2016, 46(5):1633-1638

Fractal clustering method for uncovering community of complex network

复杂网络社区的分形聚类检测方法

Guo Yu-quan , Li Xiong-fei.

郭玉泉, 李雄飞

... 0 引言自然界和人类社会中的大量系统都可以通过复杂网络加以描述^[1] ...

2012

0.0

... 这方面的研究有:Bhattacharya等^[2]分析了软件源代码,将函数抽象为节点,调用关系抽象为有向边构造图形,生成软件拓扑结构 ...

2015

0.0

... Chong等^[3]不仅构造了软件图形,还为边分配权重进行了扩展 ...

2015

0.0

... Chaikalis等^[4]将类抽象为节点,将类之间的(调用、关联、依赖)关系抽象为有向边 ...

2013

0.0

... Turnu等^[5]分析了Java、Eclipse和Netbeans大型面向对象软件系统的源代码,研究了源代码中的类和它们之间的依赖关系和整个发行版及其子项目的复杂性,结果表明,这样的系统可以被看作是复杂软件网络 ...

1999

0.0

... si等^[6]提出了BA无标度网络模型,模型基于增量增长和线性优先关系两种机制 ...

2005

0.0

... Valverde等^[7]提出了基于节点复制和边重新连接的模型 ...

2003

0.0

... Myers^[8]提出了基于重构过程的模型 ...

2000

0.0

... Dorogovtsev等^[9]提出了依赖现有节点的度数和年龄的模型 ...

2008

0.0

... Zheng等^[10]也提出了一个基于节点的度数和年龄的模型(Degree and age dependent adjustable evolution, DAAE) ...

2013

0.0

... Li等^[11]提出了一种模拟软件网络演化的模块连接机制,使用模块化连接代替在前面的模型中采用的单节点连接,因为将面向对象系统模块化与现实世界软件本质上更加相似 ...

2016

0.0

. 2016, 27(2):231-246 DOI:doi:10.13328/j.cnki.jos.004847

Modeling complex collaboration network for service-oriented software based on execution behaviors

基于服务交互行为的复杂服务协同网络建模

Zhang Xi-zhe , L#cod#x000fc; Tian-yang , Zhang Bin.

张锡哲, 吕天阳, 张斌

随着分布式计算技术的发展,以自治的服务协同与互操作为主要构造手段、结构与行为随需而变的面向服务的软件系统已成为当前主流的软件架构,分析并理解服务交互行为对于这类复杂软件系统的开发、维护和运营具有重要意义.针对面向服务的软件系统中基本构成元素Web服务的复杂交互执行行为,考虑到服务自治性及系统规模化所带来的复杂性,借鉴复杂网络建模分析方法,提出了一种考虑服务行为特征的服务动态行为生长演化模型.模型首先以真实服务的服务结构数据为基础,以服务间参数关联关系为核心,通过参数匹配建立服务结构网络作为基本连通性约束,代表可能发生交互关系的服务.然后,基于服务间的择优选择、组合交互及动态重组等特性对面向服务的软件系统生长演化及动态执行行为进行了仿真建模.在Seekda及QWS数据集上进行了仿真实验,结果表明:与传统的软件系统的层次性结构有所不同,由自治的Web服务所构成的软件系统具有更强的模块性;与系统中个体服务演化规则,如择优连接及动态重组相比,服务结构网络的性质对系统最终形态有更重要的影响,相关结果对大规模服务软件的构建及分析具有重要的指导意义.

... 张锡哲等^[12]提出一种新颖的基于复杂网络的服务软件行为演化模型,在大量真实服务数据的基础上,考察了面向服务的软件系统的演化仿真并分析其拓扑特征,与传统软件所构成的软件网络进行了对比,指出面向服务的软件系统特有的特征规律 ...

2011

0.0

... 还有一些模型也从不同的角度模拟了软件网络演化这一过程^[13] ...

2002

0.0

... 的特性^[14] ...

1999

0.0

... si等^[15]提出了无标度网络(Scale-free networks)模型,具有幂律分布的网络被称为无标度网络,其度分布具有胖尾现象,实验结果表明许多现实的大规模网络的度分布服从幂律分布 ...