关联分析一般指基于某种相关性测度, 评价两个变量间的相似程度, 测度得分值越大, 表示两个变量关联程度越大^[4]。

关联测度的优劣可采用普适性^[5]和等价性^[2]两个指标来度量。普适性表示该测度方法所能检测到的函数关系的类型数量, 检测到的函数关系预测越多, 其普适性越好。如Pearson相关系数仅对线性函数关系敏感, 不能有效捕获非线性函数关系, 普适性较差。公平性表示等噪音的任意函数具有相等的关联测度值。

为解决大数据非线性关联分析, 由Reshef等^[2]在2011年提出MIC测度, 其本质上是计算两两变量间的互信息值, 但其在互信息计算过程中采用的是不等间隔寻优法, 并对互信息值进行归一化矫正, 取值范围为[0, 1]。不等间隔寻优使得MIC具有普适性的优点, 归一化矫正使其具有等价性优点。

1.2.1 普适性

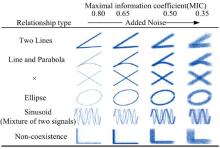
普适性是MIC最为重要的优点, 即对任意函数关系, 无论线性、非线性关系, 在无噪音时, 其得分值均最大为1, 面对两个无关系的独立变量, 其得分值为0。表1列出了MIC与几种常用的相关性测度^[2], 如Pearson相关系数^{[6, 7]}、Spearman相关系数^[8]、基于核密度估计的互信息Mutual Information^[2]、CorGC系数^[9]等, 对不同函数关系的测度情况。

由表1可知, 以上5种测度均能有效检测出线性函数关系“ Linear” 。Pearson相关系数属于经典的线性相关测度, 仅能较好地检出“ Linear” 线性关系, 对Cubic、Exponential、Parabolic拟线性关系有部分检测能力, 对其他复杂非线性关系基本无法检测。Mutual Information互信息、CorGC测度较Pearson线性关系普适性有提升, 对Parabolic等非线性函数关系有一定的检测能力, 但其普适性均弱于MIC测度。对于表中全部函数关系, MIC得分值均为1, 表明了其优异的普适性特征。

表1

Table 1

表1(Table 1)

表1 不同函数关系下的多种测度值 Table 1 Values of different functions in different measures Relationshiptype 函数 MIC Pearson Spearman Mutual Information CorGC Random 随机 0.18 -0.02 -0.02 0.01 0.19 Linear y=x 1 1 1 5.03 1 Cubic y=128(x-1/3)3-48(x-1/3)2-12(x-1/3)+2 1 0.61 0.69 3.09 0.98 Exponential y=1010x-1 1 0.7 1 2.09 0.94 Sinusoidal 1 y=sin(16π x)+x 1 -0.09 -0.09 0.01 0.36 Periodic/Linear y=sin(10π x)+x 1 0.33 0.31 0.69 0.49 Parabolic y=4(x-1/2)2 1 -0.01 -0.01 3.33 1 Sinusoidal 2 y=sin(13π x)+x 1 0 0 0.01 0.4 Sinusoidal 3 y=sin[7π x(1+x)] 1 -0.11 -0.11 0.02 0.38

表1 不同函数关系下的多种测度值 Table 1 Values of different functions in different measures

1.2.2 等价性

如表1所示, 互信息测度除存在普适性差的缺陷外, 其得分值为[0, +∞ ], 存在不同数据间可比性差的缺点。给定两种函数关系, 若加上等水平的噪音, 其相关系数理应相同, 若某一测度指标计算获得的相关系数差异越小, 表明该测度等价性越高, 反之等价性越差。图1基于6种函数关系示例了MIC的等价性^[2]。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 不同函数关系不同噪音下的MIC值Fig.1 MIC values of different functions under different noise

由图1可知, 随着噪音增加, 变量间的相关性降低, MIC值降低, 对相同的噪音水平, 不同函数的MIC值接近, 显然MIC具有较好的等价性。

MIC在本质上是基于互信息的, 但变量的离散化需要进行遍历寻优, 属于计算密集型方法^[10]。对大样本数据, 遍历算法并不可行, David等^[2]基于动态规划算法给出了快速近似算法。对给定的两个变量x₁、x₂, 其离散化分段点寻优, 矫正过程如下:

(1)x₁ 均分。假定x₁仅离散化为两段, 首先按升序排列变量x₁, 再根据样本数量相等的原则, 按排序均分x₁为两段, 该过程即固定x₁为两段。

(2)在x₁均分两段情况下, 确定变量x₂潜在分段点。互信息具有分段数越多得分越高的特点, 为保证MIC得分的准确性, 规定x₁变量与x₂变量的分段数必须满足限制x× y≤ B(B=n^0.6), x表示变量x₁的分段数, y表示变量x₂的分段数, n表示成对的样本数目。例如, 在x₁已均分两段时, 变量x₂最多可划分B/2段。一方面为保证x₂分段准确性, 另一方面为降低计算复杂度, 采用均分的原则, 可将x₂平均分为c× B/2个小簇, c可根据数据样本数自行给定, 如5或15等, 并且在均分x₂过程中, 对应x₁取值相等的样本应划分在同一个小簇中。这些将x₂划分为不同小簇的样本点即为x₂的潜在分段点。

(3)基于动态规划的x₂变量分段点寻优。遍历上述第(2)步所给定的x₂潜在分段点(保持x₁均分两段不变), 并计算每种离散情况下的x₁与x₂的互信息值, 计算公式如下:

I(x₁, x₂)=H(x₁)+H(x₂)-H(x₁, x₂)(1)

定义最大互信息值对应的分段点为x₂分两段的最优分段点。在此基础上, 从剩余潜在分段点中确定最优的第3个分段点, 直至第B/2-1个最优分段点, 共划分为B/2段。

(4)x₁变量均分多段寻优。当x₂仅离散化为两段时, x₁最多可被均分B/2段, 依次将变量x₁均分为3, 4, …, B/2段, 并重复第(2)(3)步, 获得对应x₂变量的最优离散化段数。最终可获得一个不完全的寻优互信息得分矩阵I_ij, 矩阵中的每一元素为x₁均分为i段、x₂离散化j段时x₁与x₂之间的互信息值。

(5)互信息矫正。上述得到的互信息经最小分段数矫正即可转换为对应的MIC值, 矫正公式为:

MIC_ij=I_ij/log₂(min([i, j])) (2)

(6)均分方向互换, 将x₂均分, 寻优x₁变量, 重复第(2)~(5)步, 可获得均分x₂方向的MIC得分矩阵。

(7)MIC得分定义为上述两个得分矩阵中最大的得分值。

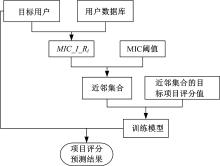
假定n个用户对m个项目评分, 第i 个用户对第j个项目的评价得分为R_ij, R_ij{i=1, 2, …, n; j=1, 2, …, m}。对目标用户I, 可基于MIC得分表示其与其他用户偏好性的相似程度, 分别记为MIC_I_R_i{i=1, 2, …, n}。

按MIC_I_R_i大小排序, 目标用户I的近邻集合则为与其相似性最高的K个用户, 记为U_{I_k}, 对不同的阈值, 1≤ K≤ n。

本文所用SVM算法基于采用林志仁教授等^[11]开发的LIBSVM平台实现, 该程序包括Svmtrain与Svmpredict两个主程序。前者用于模型训练, 后者用于预测独立测试样本。

以均方误差(Mean square error, MSE)评价预测模型的优劣, 真实值与预测值间差异越小, MSE越小, 即模型预测能力越好, 其计算公式如下:

MSE= ∑i=1n(yi-y˙i)2/n (3)

式中:y_i为目标用户对第i个项目的真实评分; y^i为预测的评分值; n为被预测的目标用户数。

为验证近邻集合影响项目评分的预测效果, 从近邻集合与建模方法两个方向设计了参比模型。在近邻集合筛选方面, 选择MIC、Pearson相关系数、互信息(MI)、CorGC相关系数4种关联测度, 预测方法均为SVM。基于MIC筛选获得近邻集, 本文选择K近邻法(KNN)、多元线性回归(MLR)、人工神经网络(ANN)^[12]、SVM四种建模方法。基于MIC近邻集合筛选的项目评分预测模型构建过程如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 基于MIC的推送模型项目评分预测模型Fig.2 Push model project score prediction model based on MIC

本文所用仿真数据为MovieLens网站开源的电影评分数据, 数据集包含了943位用户对1682部电影的100 000条评分记录, 评分值分为5个等级, 用1~5代表, 用户对某部电影越感兴趣, 评分值越大。表2为部分用户对20部电影的评分情况。为降低数据稀疏性, 将1682部电影合并为Action、Children's、Crime、Documentary、Sci-Fi、War等 18种类型。每个类型的评分值为用户对该类型电影评分的平均值。表3为部分合并后的评分矩阵。将全部数据随机分成两部分, 80%用户作为训练集, 20%用户作为测试集。

表2

Table 2

表2(Table 2)

表2 前50个户对前20部电影的评分表 Table 2 Scores of top 50 households on top 20 films 用户编号 电影编号 1 2 3 4 5 6 7 8 9 10 … 20 1 5 3 4 3 3 5 4 1 5 3 … 4 2 4 0 0 0 0 0 0 0 0 2 … 0 3 0 0 0 0 0 0 0 0 0 0 … 0 4 0 0 0 0 0 0 0 0 0 0 … 0 5 4 3 0 0 0 0 0 0 0 0 … 0 6 4 0 0 0 0 0 2 4 4 0 … 0 7 0 0 0 5 0 0 5 5 5 4 … 0 8 0 0 0 0 0 0 3 0 0 0 … 0 9 0 0 0 0 0 5 4 0 0 0 … 0 10 4 0 0 4 0 0 4 0 4 0 … 0 ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ 50 0 0 0 0 0 0 0 0 4 0 … 0 注:0表示该用户对该电影未评分。

表2 前50个户对前20部电影的评分表 Table 2 Scores of top 50 households on top 20 films

表3

Table 3

表3(Table 3)

表3 合并后的评分表 Table 3 Combined scores 用户编号 电影类型 Action Adventure Animation Children's Comedy Crime Documentary Drama Fantasy … Western 1 3.33 2.93 3.33 2.20 3.47 3.44 4.80 3.93 3.50 … 3.67 2 3.80 4.33 4.00 3.00 3.81 3.78 NaN 3.83 3.00 … NaN 3 2.79 3.50 NaN NaN 2.58 3.00 5.00 2.91 NaN … NaN 4 3.88 3.50 NaN NaN 5.00 4.75 5.00 4.50 NaN … NaN 5 3.14 3.24 3.79 2.45 3.00 3.89 NaN 2.67 2.50 … 2.50 6 3.36 3.45 3.40 3.05 3.50 3.71 4.00 3.73 2.33 … 3.60 7 3.88 4.00 4.46 4.06 3.83 4.00 4.20 4.21 4.14 … 3.94 8 4.08 3.82 NaN 1.33 2.40 4.11 NaN 4.24 NaN … 4.33 9 5.00 5.00 NaN NaN 4.50 NaN NaN 4.00 NaN … NaN 10 4.28 4.36 4.14 4.25 3.94 4.50 4.00 4.27 4.00 … 4.60 ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ 50 NaN NaN NaN NaN 4.50 3.20 5.00 3.24 NaN … NaN 注:NaN表示未评分。

表3 合并后的评分表 Table 3 Combined scores

对每个待测样本, 基于给定相似性测度, 从训练集中选择相似性最大的K个样本构建SVM预测模型。本次仿真K取值为60。4种预测模型结果见图3。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同相似性测度的预测精度Fig.3 Prediction accuracy of different similarity measures

由图3结果可知, 基于MIC关联测度的模型预测效果最好; CorGC测度能部分检测非线性关联, 其筛选近邻集合的预测精度略低于MIC模型, 但明显优于线性测度Pearson相关系数和MI。

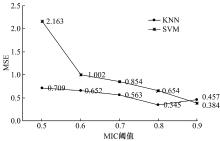
MIC测度所选近邻集合预测精度最高, 因此, 选择该近邻集合作为训练样本, 用于比较不同建模方法预测性能。图4为KNN、ANN、MLR和SVM四种方法的预测效果。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 不同建模方法预测精度Fig.4 Prediction accuracy of different modeling methods

在4种建模方法中, MLR模型预测精度最差, MSE为2.115, 该模型属于典型线性模型, 表明用户评分之间呈现复杂非线性关系, SVM模型属于非线性模型, 其预测精度在参比模型中最优。KNN以近邻集合项目评分均值作为预测样本, 信息完整性不足, 影响预测精度。MIC测度能普适性检测线性、非线性关系, 能筛选信息完整的近邻集合, 所以KNN模型也能获得较优结果。

设置不同水平的MIC阈值, 得到多个近邻集合, 以此为预测样本构建预测模型, 结果见图5。

由图5结果可知, SVM模型对MIC阈值不敏感, 当阈值从0.8增加到0.9时, 其预测精度小幅度下降, 可能是因为训练样本减少导致。KNN模型稳定性较SVM差。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 MIC不同阈值对预测精度的影响Fig.5 Effects of different MIC threshold on prediction accuracy