基于节点可靠度的无线传感器网络拓扑控制算法

引用本文

刘洲洲, 彭寒. 基于节点可靠度的无线传感器网络拓扑控制算法. 2018, 48(2): 571-577
LIU Zhou-zhou, PENG Han. Topology control algorithm based on node reliability in WSN. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 571-577 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161348
Permissions

基于节点可靠度的无线传感器网络拓扑控制算法

刘洲洲^1,², 彭寒²

1.西安航空学院电子工程学院,西安 710077

2.西北工业大学计算机学院,西安 710072

作者简介:刘洲洲(1981-),男,在站博士后.研究方向:无线传感器网络.E-mail:nazi2005@126.com

基金项目:陕西省自然基础研究计划面上项目(2017JM6096); 西安市科技计划项目(2017076CG/RC039(XAHK001))

摘要

针对无线传感器网络节点在数据传输过程中易面临能量耗尽和数据拥塞失效的问题,通过构建节点可靠度模型,获得了网络在保证节点可靠度最大且网络生存时间最长的条件下最优节点度的取值。进而依据最优节点度的取值,提出了一种基于节点度调整的无线传感器网络拓扑控制算法(TCNR)。仿真实验结果表明,TCNR算法极大减少了拓扑数据传输过程中的拥塞程度,增强了拓扑结构的健壮性,并有效延长了网络生存时间。

关键词: 计算机应用; 无线传感器网络; 拓扑控制; 数据拥塞; 能量耗尽

中图分类号:TP394.1 文献标志码:A 文章编号:1671-5497(2018)02-0571-07

Topology control algorithm based on node reliability in WSN

LIU Zhou-zhou^1,², PENG Han²

1.School of Electronic Engineering, Xi'an Aeronautical University, Xi'an 710077, China

2.School of Computer Science, Northwestern Polytechnical University, Xi'an 710072, China

Abstract

During data transmission in Wireless Sensor Network (WSN), the nodes are always faced with the problems of energy depletion and data congestion. To solve these problems, this paper establishes a mathematical model of node reliability, and the optimal value of the node degree is obtained by maximizing the node reliability and the network lifetime. Then, in accordance with the optimal value of the node degree, a Topology Control based on Node Reliability (TCNR) algorithm is put forward. Simulation results show that the TCNR algorithm can greatly reduce the congestion degree in data transmission, enhance the robustness of the topological structure, and effectively prolong the WSN lifetime.

Key words: computer application; wireless sensor networks; topology control; data congestion; energy depletion

Show Figures

0 引言

无线传感器网络(WSN)作为物联网发展的重要组成部分^{[1, 2]}, 与其他通信网络相比, 具有部署规模大、节点冗余度高、分布环境恶劣和节点自身资源有限等特点^[3]。对于大规模部署的WSN, 良好的拓扑结构是网络生存能力的重中之重^[4], 也是实现各种网络协议的基础。

当前对于WSN拓扑结构控制算法大多是从节能角度出发考虑的, 其中, 文献[5]构建了一种节能拓扑(Energy-aware evolution model, EAEM), 节点的择优连接概率不仅仅取决于节点度, 还与节点的剩余能量有关。文献[6]在局域世界内建立适应度模型, 通过调节节点的适应度因子, 最终演化出能耗更均衡的无标度拓扑, 更适用于WSN的实际应用。文献[7]构建的拓扑, 通过节点的剩余能量限制网络中的最大节点度, 有效地均衡了网络负载, 减小了能量耗尽对拓扑的影响。文献[8]基于节点综合故障模型约束网络节点度, 构建了节能容错的拓扑结构。然而, 目前工程上所用的WSN节点大多受到节点能量和容量的限制, 其中节点容量是指节点能够转发数据量多少的能力, 现有WSN拓扑控制算法大多仅仅考虑节点能量方面的优化, 考虑节点容量方面的研究较少, 而节点容量正是引起节点拥塞的重要原因, 目前研究的节点拥塞控制机制都是在节点发生拥塞时才采取一定的拥塞控制措施。其中, 文献[9]通过分析得出, 距离SINK节点越近的节点越容易发生拥塞, 然后依据节点距离SINK节点的远近控制节点度, 最终达到控制网络数据拥塞的目的。文献[10, 11]通过判断节点缓存内数据队列长度来判断节点的拥塞程度, 然后通过控制节点度达到减弱拓扑拥塞的目的。文献[12]运用博弈理论来分析单个传感器节点的分布式决策过程, 以此达到降低网络能耗的目的, 但是仅在理论层面上给出了理想的能耗均衡WSN结构, 并没有考虑节点度对网络性能的影响。文献[13]考虑了节点在广播时的干扰和能量消耗, 通过优化每个节点的传动功率以达到优化网络结构的目的, 以此来降低节点拥塞。文献[14]从博弈论的视角出发考虑单个节点度对网络性能的影响, 从理论上分析了WSN系统存在最优的纳什均衡。但是, 以上文献均没有考虑到当无线传感器网络节点大规模密集部署时, 在突发数据流引发拥塞后, 再采用拥塞控制措施也不一定可以完全避免节点拥塞, 则很有可能导致节点能量过快耗尽, 进而导致全局网络受损。

针对上述分析, 本文提出了一种基于节点可靠度拓扑控制算法(Topology control based on node reliability in wireless sensor networks, TCNR), 首先依据节点能量耗尽概率和拥塞失效概率构建节点可靠度模型, 并以节点可靠度最大和网络生存时间最长为约束条件, 获得了最优节点度的取值, 最终通过最优节点度约束网络所有节点的节点度, 根据仅改变最优节点度取值, 可以有效地使整个网络拓扑性能得到优化, 从而达到延长网络生存时间的目的。

1 问题模型

WSN在数据传输过程中, 节点能量耗尽和数据拥塞是造成数据传输失败的重要原因, 本文通过对节点能量耗尽失效概率和数据拥塞造成节点失效概率建模, 得出了节点可靠度模型, 并通过分析节点可靠度与网络参数的关系, 最终得出了最优节点度的取值。

1.1 节点可靠度建模

本文将节点i可靠度R(i)定义为:

R(i)=1-f_e(i)f_c(i)(1)

式中:f_e(i)为节点i能量耗尽失效的概率; f_c(i)为节点i数据拥塞造成节点失效的概率。

节点能量耗尽失效和数据拥塞造成节点失效的概率越大, 节点的可靠度就越小; 节点能量耗尽失效和数据拥塞造成节点失效的概率越小, 节点的可靠度就越大。

由文献[15]可知, 节点能量耗尽的概率f_e(i)取决于节点i的初始能量值E₀(i)、能量消耗值E_c(i)和网络运行时间t, 即:

f_e(i)=1- $\begin{matrix} e^{- \frac{1}{E_{0} (i) / E_{c} (i)} t} \end{matrix}$ (2)

采用一阶无线通信能耗模型^[16], 两个相距为d的节点发送l bit数据所消耗的能量E_tx为:

E_tx=E_elecl+ε _ampld²(3)

式中:E_elec为射频传输系数; ε _amp为发送装置放大系数。

节点接收l bit数据消耗能量E_rx取决于信号接收电路消耗的能量:

E_rx=E_elecl(4)

那么, 节点i在单位时间内消耗的总能耗E_c(i)可由下式计算得到:

E_c(i)=E_tx+E_rx=2E_elecl+ε _ampld²(5)

假设N个节点随机部署在监测区域G(面积为A)上, 由概率论可知节点坐标(X, Y)具有概率密度函数g(x, y)为:

g(x, y)= $\begin{matrix} \{\begin{matrix} 1 / A, (x, y) \in G \\ 0, 其他 \end{matrix} \end{matrix}$ (6)

则节点落入以通信距离d为半径的圆域D内的概率P为:

P=g(x, y)dxdy= $\begin{matrix} \frac{π d^{2}}{A} \end{matrix}$ (7)

因此, 可得节点传输距离d与其节点度k之间存在如下关系:

k=NP=N $\begin{matrix} \frac{π d^{2}}{A} \end{matrix}$ (8)

此时, 将式(8)代入式(5), 可得节点i的能耗值E_c(i)随其节点度k的变化关系:

E_c(i)=E_tx+E_rx=2E_elecl+ $\begin{matrix} \frac{ε_{amp} lA}{Nπ} \end{matrix}$ k(9)

再将式(9)代入式(2)可得节点由能量耗尽引起节点失效的概率f_e(i)为:

f_e(i)=1-e^-⁽^a+bk⁾^t(10)

式中:a= $\begin{matrix} \frac{2 E_{elec} l}{E_{0} (i)} \end{matrix}$ ; b= $\begin{matrix} \frac{ε_{amp} lA}{Nπ E_{0} (i)} \end{matrix}$ 。

考虑到WSN引起节点拥塞的重要原因是其负载大于其最大容量。通常WSN节点负载是指节点在某一时刻需要转发的信息量, 假设节点i的节点度为k, 任意节点与其邻居节点数据交换的信息量为l, 那么在任意时刻节点i的最大负载L定义为:

L=kl (11)

由于WSN节点受到硬件资源的限制, 节点具有固定的容量, 如果在某一时刻其负载量超过其容量, 就会发生拥塞。其中, 节点发生拥塞的概率与其负载量成正比, 节点负载量越大, 其发生拥塞的概率就越大。假设节点拥有固定的容量C₀, 那么在任意时刻节点由数据拥塞是造成节点失效的概率f_c(i)定义为:

f_c(i)= $\begin{matrix} \frac{1}{C_{0} - L} \end{matrix}$ = $\begin{matrix} \frac{1}{C_{0} - kl} \end{matrix}$ (12)

为了满足概率范围为[0, 1]的条件, 式(12)中C₀-kl> 1, 可得k< $\begin{matrix} \frac{C_{0} - 1}{l} \end{matrix}$ , 将式(10)和式(12)代入式(1)可得节点可靠度函数为:

R(i)=1- $\begin{matrix} \frac{1 - e^{- (a + bk) t}}{C_{0} - kl} \end{matrix}$ , k< $\begin{matrix} \frac{C_{0} - 1}{l} \end{matrix}$ (13)

式(13)即为节点可靠度数学模型, 由式(13)可知, 节点可靠度不仅与节点度有关, 也与网络的生存时间相关。下面利用所获得的节点可靠度数学模型对节点度进行量化分析, 为获取依据最优节点度调整的WSN拓扑演化模型提供理论依据。

1.2 基于节点可靠度的最优节点度量化分析

对于一个网络I, 其拓扑参数应满足如下条件:为提高拓扑的可用性, 网络须保证一定的生存时间t_min, 即t≥ t_min; 为了保证网络的连通性, 网络I须维持一定的节点度下限k_min, 即≥ k_min。为了分析拓扑参数对节点可靠度的影响, 得出网络中节点可靠度最大时, 网络生存时间与节点度的关系, 引出如下定理。

定理对于一个网络I, 如果其运行时间t≥ t_min, 且网络节点度符合k_min≤ < $\begin{matrix} \frac{C_{0} - 1}{l} \end{matrix}$ , 则当节点可靠度为R₀(i)=1- $\begin{matrix} \frac{1 - e^{- (a + b k_{\min}) t_{\min}}}{C_{0} - k_{\min} l} \end{matrix}$ 时, 网络中的节点可靠度最大。其中, t_min为网络预设运行时间, k_min为节点度下限, k_max为节点度上限值。

证明由t≥ t_min可得, 节点可靠度f(i)符合:

R(i)≤ 1- $\begin{matrix} \frac{1 - e^{- (a + bk) t_{\min}}}{C_{0} - kl} \end{matrix}$ (14)

又根据k≥ k_min可得:

R(i)≤ 1- $\begin{matrix} \frac{1 - e^{- (a + bk) t_{\min}}}{C_{0} - kl} \end{matrix}$ ≤ 1- $\begin{matrix} \frac{1 - e^{- (a + b k_{\min}) t_{\min}}}{C_{0} - k_{\min} l} \end{matrix}$ (15)

所以有:

R(i)≤ 1- $\begin{matrix} \frac{1 - e^{- (a + b k_{\min}) t_{\min}}}{C_{0} - k_{\min} l} \end{matrix}$ (16)

因此, 如果网络中节点可靠度满足:

R₀(i)=1- $\begin{matrix} \frac{1 - e^{- (a + b k_{\min}) t_{\min}}}{C_{0} - k_{\min} l} \end{matrix}$ , k_min≤ < $\begin{matrix} \frac{C_{0} - 1}{l} \end{matrix}$

则网络中所有节点可靠度最大。

上述定理得出了网络在节点可靠度最大时R₀(i)与拓扑参数的关系, 则当网络中节点失效概率满足R(i)=R₀(i), 根据式(13)可得:

t= $\begin{matrix} \frac{\ln [1 - (C_{0} - kl) (1 - R_{0} (i))]}{- (a + bk)} \end{matrix}$ (17)

由于当式(17)中分子1-(C₀-kl)(1-R₀(i))< 0时, 函数值不存在, 因此可得:

k> $\begin{matrix} \frac{C_{0} (1 - R_{0} l) - 1}{l (1 - R_{0} l)} \end{matrix}$

当 $\begin{matrix} \frac{C_{0} (1 - R_{0} l) - 1}{l (1 - R_{0} l)} \end{matrix}$ < k< $\begin{matrix} \frac{C_{0} - 1}{l} \end{matrix}$ 时, 对式(17)进行一阶求导可得:

t^'=dt/dk= $\begin{matrix} \{- \frac{l (1 - R_{0} (i)) (a + bk)}{1 - (C_{0} - kl) (1 - R_{0} (i))} \end{matrix}$ +

$\begin{matrix} \frac{}{} bln [1 - (C_{0} - kl) (1 - R_{0} (i))]\} / \end{matrix}$ (a+bk)² (18)

由于0< 1-(C₀-kl)(1-R₀(i))< 1, 所以ln[1-(C₀-kl)(1-R₀(i))]< 0, 又- $\begin{matrix} \frac{l (1 - R_{0} (i)) (a + bk)}{1 - (C_{0} - kl) (1 - R_{0} (i))} \end{matrix}$ < 0且(a+bk)²> 0, 因此可得t'< 0, 也就是说, 式(17)在 $\begin{matrix} \frac{C_{0} (1 - R_{0} l) - 1}{l (1 - R_{0} l)} \end{matrix}$ < k< $\begin{matrix} \frac{C_{0} - 1}{l} \end{matrix}$ 范围内单调递减, 由于节点度k为整数, 因此可得:当k₀= $⌈\frac{C_{0} (1 - R_{0} l) - 1}{l (1 - R_{0} l)}⌉$ 时, 网络生存时间最长。

综上可知, 由于突发数据流引发拥塞后, 再采用拥塞控制措施也不一定可以完全避免节点拥塞, 很有可能导致节点能量过快耗尽, 本文通过理论分析获得了在节点可靠度最大和网络生存时间最长的条件下最优节点度k₀的取值, 通过最优节点度约束网络所有节点的节点度, 相比目前已有的研究^[10^-^14], 根据仅改变最优节点度取值, 优化了网络拓扑性能, 延长了网络生命周期。

2 TCNR算法

TCNR算法主要由以下4个阶段组成:

(1)信息交换阶段:在拓扑结构形成开始, 各节点都以最大功率广播“ 握手” 消息, 任意收到“ 握手” 消息的节点建立其自身的邻居列表。以节点i为例, 邻居列表的表头格式如表1所示。其中, ID(j)表示节点i的邻居节点j的ID; (x_j, y_j)表示节点j的地理位置; d(i, j)为i和j之间的距离; mark(j)为状态标识, 初始记为0。其中, 任意节点的邻居列表均依据节点之间的通信距离进行升序排序。

表1 节点i的邻居列表的表头格式 Table 1 Header format for node i neighbor list

(2)邻居排序阶段:节点i广播NOTICE信息, 其中NOTICE信息包含节点iID及邻居列表信息。收到NOTICE信息的邻居节点判断自身局域范围内的通信状态, 并建立局域链路列表, 其表头格式见表2。其中, 假设j₁、j₂为节点i的邻居节点, d(j₁, j₂)为节点i的邻居节点j₁和j₂间的距离, ID(j₁)和ID(j₂)分别为j₁、j₂的ID, sign(j₁, j₂)为状态标识, 初始设定为0。区域链路列表建立后, 节点i按照通信距离d(j₁, j₂)对其局域链路列表进行升序排列, 如果j₁和j₂之间不存在通信路径, 将链路状态标识sign(j_i, j_j)更新为1, 直至与所有邻节点判断完成为止, 最后删除sign标记为0的链路项信息。

表2 节点i局域链路列表的表头格式 Table 2 Header format for node i local link list

(3)链路选择阶段:依据区域链路列表, 节点i对其邻居节点广播包含自身ID和局域链路列表信息的CONNECT数据包。根据所接收到的CONNECT数据, 以链路双向性原则确定其区域链路, 将其sign标记为2, 删除标记为1的链路项信息, 进而寻找区域链路列表中由自身出发的链路项, 并将其邻居列表中的相应标识位mark更新为1, 统计其数目记为k_min, 计算出最优节点度k₀与k_min的差值。在此基础上, 按距离升序依次将个邻居列表中标识为0的节点标记为2, 删除状态不为1的邻节点信息项。

(4)功率调整阶段:节点i根据链路选择阶段确定其自身发射功率, 同时应保证与新的邻居节点皆能正常通信。

3 仿真实验与性能分析

为了验证TCNR拓扑控制算法的性能, 本文采用MATLAB 2012a仿真工具, 对具有节能代表性的FTEL算法^[16]和路径优化算法(Path optimization algorithm, POA)^[17]进行仿真实验对比, 并且假定拓扑结构均为不分簇的同构平面结构, 仿真实验参数见表3。其中, 每一个实验结果都是50次实验的平均值。

表3 实验环境参数 Table 3 Experimental environmental parameters

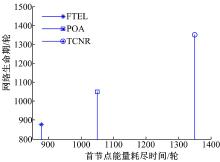
为了解析得到网络中最优节点度k₀的最优取值, 首先根据构建的节点可靠度模型和表3中的参数取值, 并结合式(18)可以得出最优节点度在k₀=4时网络运行时间达到最大, 然后依据TCNR拓扑控制算法优化网络拓扑, 与FTEL和POA算法进行性能对比。

3.1 拓扑结构对比

在1000 m× 1000 m的区域随机布撒100个节点, 依照TCNR、FTEL和POA三种拓扑控制算法得到的拓扑结构如图1所示。对比TCNR和FTEL拓扑结构可以看出, FTEL中存在较多度为1的节点和一部分度较大的节点, 而TCNR图谱结构较为均匀, 拓扑中的节点度都接近4, 可以有效避免节点拥塞和能量耗尽失效。TCNR与POA拓扑相比, 大大减少了冗余链路的存在, 有效避免了不必要的节点能耗, 延长了络生存时间。

	Figure Option View Download New Window
	图1 拓扑结构对比Fig.1 Comparison of topological structure

3.2 网络平均节点度对比

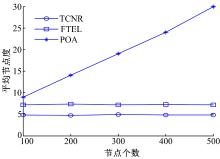
网络的平均节点度通常表示为节点与邻居节点通信链路的数量, 因此, 拓扑连通的情况下可以通过平均节点度的大小来衡量拓扑的冗余程度和干扰程度, 如果平均节点度越大, 冗余链路越多就会造成网络能耗越快, 而且链路之间的干扰也会增大, 本文对TCNR、FTEL和POA三种拓扑控制算法的平均节点度进行了对比。分别在1000 m× 1000 m的区域随机布撒100、200、300、400和500个节点, 依照TCNR、FTEL和POA三种拓扑控制算法, 得到3种拓扑结构的平均节点度如图2所示。由图2可以看出, TCNR算法的平均节点度在5左右, POA算法平均节点度在7左右, FTEL算法随节点数的增加平均节点度也在逐渐增大。TCNR算法与POA和FTEL算法相比比降低了网络平均节点度, 说明TCNR算法通过最优节点度的限制有效控制了网络的平均节点度, 减少了网络干扰, 增强了网络健壮性。

	Figure Option View Download New Window
	图2 平均节点度对比Fig.2 Comparison of average node degree

3.3 网络健壮性对比

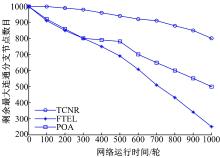
网络在数据传输过程中通常会伴随着节点失效, 当节点失效后, 拓扑中剩余最大连通分支的数目可以作为网络健壮性的衡量标准。为了对比3种网络的健壮性, 在1000 m× 1000 m的区域随机布撒100个节点, 依照TCNR、FTEL和POA三种拓扑控制算法运行拓扑, 在每轮数据传输过程中, 节点均与其邻居节点进行数据交换, 节点按照一阶能耗模型计算剩余能量^[12], 节点在能量耗尽和拥塞时均按照死亡节点处理, 最后统计网络中剩余最大连通分支节点数目, 剩余最大连通数目越大表示网络健壮性越好, 得到的网络健壮性对比图如图3所示。由图3可以看出, 3种拓扑结构在网络运行1000轮的情况下, TCNR拓扑剩余最大连通数目将近80%, POA拓扑剩余最大连通分支将近50%, FTEL拓扑剩余最大连通分支仅剩22%左右, 说明TCNR算法通过拓扑控制有效提高了拓扑结构的健壮性。

	Figure Option View Download New Window
	图3 网络健壮性对比Fig.3 Comparison of network robustness

3.4 网络生命期对比

网络的生存时间通常定义为首节点失效的时间, 也就是说, 在数据传输过程中, 拓扑中出现首个节点失效的时间可以作为网络生命期的衡量标准。因此, 在仿真实验中将拓扑出现首节点失效的时间记为网络的生存时间, 图4给出了TCNR、FTEL和POA三种模型的网络生存时间, 从图4中可以看出, TCNR算法拥有最长的网络生命期, 相对POA算法的网络生命期提升了将近30%, 相对FTEL提升了将近50%, 说明TCNR拓扑通过控制网络节点度有效均衡了网络能耗, 延长了网络生命期。

	Figure Option View Download New Window
	图4 网络生命期对比Fig.4 Comparison of network life cycle

4 结束语

通过构建节点可靠度模型以及理论分析得出了在节点可靠度最大且网络生存时间最长的条件下的最优节点度, 进而依据最优节点度提出了一种基于节点度调整的拓扑控制算法TCNR。最后, 通过仿真验证了该拓扑的节能性和可靠性。利用TCNR模型, 仅通过改变最优节点度取值就可以产生综合性能优化的拓扑, 为WSN拓扑控制算法奠定了良好的基础。今后研究工作的重点是, 在实际应用环境下测试本文工作的有效性以提高其实用性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Lin T Y, Santoso H A, Wu K R. Global sensor deployment and local coverage-aware recovery schemes for smart environments[J]. IEEE Transactions on Mobile Computing, 2015, 14(7): 1382-1396. [本文引用:1]
[2]	Mahboubi H, Moezzi K, Aghdam A G, et al. Distributed deployment algorithms for improved coverage in a network of wireless mobile sensors[J]. IEEE Transactions on Industrial Informatics, 2014, 10(1): 163-174. [本文引用:1]
[3]	Mahboubi H. Distributed deployment algorithms for efficient coverage in a network of mobile sensors with no identical sensing capabilities[J]. IEEE Transactions on Vehicular Technology, 2014, 63(8): 3998-4016. [本文引用:1]
[4]	Mahboubi H, Aghdam A G. Distributed deployment strategies to increase coverage in a network of wireless mobile sensors[C]∥Proceedings of 2013 American Control Conference (ACC), Washington, 2013: 17-19. [本文引用:1]
[5]	Zhu H L, Luo H, Peng H P, et al. Complex networks-based energy-efficient evolution model for wireless sensor networks[J]. Chaos, Solitons and Fractals, 2009, 41(4): 1828-1835. [本文引用:1]
[6]	Qi X Q, Ma S Q, Zheng G Z. Topology evolution of wireless sensor networks based on adaptive free-scale network[J]. Journal of Information and Computational Science, 2011, 8(3): 467-475. [本文引用:1]
[7]	张德干, 戴文博, 牛庆肖. 基于局域世界的WSN拓扑加权演化模型[J]. 电子学报, 2012, 40(5): 1000-1004. Zhang De-gan, Dai Wen-bo, Niu Qing-xiao. Structure of WSN topological weighted evolution model based on local domain[J]. Acta Electronic Journal, 2012, 40(5): 1000-1004. [本文引用:1]
[8]	王亚奇, 杨晓元. 一种无线传感器网络簇间拓扑演化模型及其免疫研究[J]. 物理学报, 2012, 61(9): 090202. Wang Ya-qi, Yang Xiao-yuan. Study on cluster evolution model and its immunity of wireless sensor networks[J]. Acta Physica Sinica, 2012, 61(9): 090202. [本文引用:1]
[9]	尹荣荣, 刘彬, 刘浩然, 等. 无线传感器网络中无标度拓扑的动态容错性分析[J]. 物理学报, 2014, 63(11): 110205. Yin Rong-rong, Liu Bin, Liu Hao-ran, et al. Dynamic fault tolerance analysis of scale-free topologies in wireless sensor networks[J]. Acta Physica Sinica, 2014, 63(11): 110205. [本文引用:1]
[10]	Bartolini N, Calamoneri T, Portat T FL, et al. Autonomous deployment of heterogeneous mobile sensors[J]. IEEE Transactions on Mobile Computing, 2011, 10(6): 753-766. [本文引用:1]
[11]	Chen I R, Speer A P, Eltoweissy M. Adaptive fault-tolerant QoS control algorithm for maximizing system lifetime of query-based wireless sensor networks[J]. IEEE Transactions on Dependable and Secure Computing, 2011, 8(2): 161-176. [本文引用:1]
[12]	Ren H, Meng Q H. Game-theoretic modeling of joint topology control and power scheduling for wireless heterogeneous sensor networks[J]. IEEE Transactions on Automation Science & Engineering, 2009, 6(4): 610-625. [本文引用:1]
[13]	Miyao K, Nakayama H, Ansari N, et al. LTRT: an efficient and reliable topology control algorithm for ad-hoc networks[J]. IEEE Transactions on Wireless Communications, 2010, 8(12): 6050-6058. [本文引用:1]
[14]	Nahir A, Orda A, Freund A. Topology design of communication networks: a game-theoretic perspective[J]. IEEE/ACM Transactions on Networking, 2014, 22(2): 405-414. [本文引用:1]
[15]	尹荣荣, 刘彬, 李雅倩, 等. 能量异构无线传感器网络容错拓扑研究[J]. 电子与信息学报, 2012, 34(9): 2180-2186. Yin Rong-rong, Liu Bin, Li Ya-qian, et al. Study on fault tolerant topology of energy heterogeneous wireless sensor networks[J]. Journal of Electronics & Information Technology, 2012, 34(9): 2180-2186. [本文引用:1]
[16]	刘浩然, 尹文晓, 韩涛, 等. 一种优化传感器无线网络生命周期的容错拓扑研究[J]. 物理学报, 2014, 63(4): 80-86. Liu Hao-ran, Yin Wen-xiao, Han Tao, et al. Wireless sensor network fault tolerant topology for lifetime optimization[J]. Acta Phys Sin, 2014, 63(4): 80-86. [本文引用:2]
[17]	郝晓辰, 刘伟静, 辛敏洁, 等. 一种无线传感器网络健壮性可调的能量均衡拓扑控制算法[J]. 物理学报, 2015, 64(8): 080101. Hao Xiao-chen, Liu Wei-jing, Xin Min-jie, et al. An energy balance topology control algorithm for robustness of wireless sensor networks[J]. Acta Physica Sinica, 2015, 64(8): 080101. [本文引用:1]

2015

0.0

... 0 引言无线传感器网络(WSN)作为物联网发展的重要组成部分^[1,2],与其他通信网络相比,具有部署规模大、节点冗余度高、分布环境恶劣和节点自身资源有限等特点^[3] ...

2014

0.0

2014

0.0

2013

0.0

... 对于大规模部署的WSN,良好的拓扑结构是网络生存能力的重中之重^[4],也是实现各种网络协议的基础 ...

2009

0.0

2011

0.0

2012

0.0

. 2012, 40(5):1000-1004

Structure of WSN topological weighted evolution model based on local domain

基于局域世界的WSN拓扑加权演化模型

Zhang De-gan , Dai Wen-bo , Niu Qing-xiao.

张德干, 戴文博, 牛庆肖

2012

0.0

. 2012, 61(9):090202-

Study on cluster evolution model and its immunity of wireless sensor networks

一种无线传感器网络簇间拓扑演化模型及其免疫研究

Wang Ya-qi , Yang Xiao-yuan.

王亚奇, 杨晓元

2014

0.0

. 2014, 63(11):110205- DOI:doi:10.7498/aps.63.110205

Dynamic fault tolerance analysis of scale-free topologies in wireless sensor networks

无线传感器网络中无标度拓扑的动态容错性分析

Yin Rong-rong , Liu Bin , Liu Hao-ran

尹荣荣, 刘彬, 刘浩然

It is very important in practice to avoid cascading failures by increasing the dynamic fault-tolerance of the network. Firstly, a cascading failure model is proposed in this paper, based on the characteristics of the variable load and the fixed capacity of the nodes in wireless sensor network scale-free topology. Then the influences of the load parameter and topology parameters on the fault tolerance are investigated in the case of cascading failure caused by random failure nodes. Finally the critical value of load for the large-scale cascading failure of network is deduced. Simulation result shows that the network's cascading failure fault-tolerance is positively related with the degree parameters, coefficient and power-law exponent. Researches provide regulation to avoid the cascading failure caused by the random failure nodes effectively from optimizing the parameters viewpoint.

增强网络的动态容错性对于抵御级联失效具有重要的现实意义. 根据无线传感器网络无标度拓扑中节点可变负载和恒定容量的特点建立级联失效模型,在随机节点失效下研究负载参数和拓扑参数对其级联失效容错性的影响规律,解析推导出该网络大规模级联失效的承载极限,同时模拟结果发现该网络的级联失效容错性与其度分布系数和幂指数正相关. 这为从参数优化角度抵御随机节点失效下无线传感器网络无标度拓扑级联失效危害提供了依据.

2011

0.0

2011

0.0

2009

0.0

... 1000 m的区域随机布撒100个节点,依照TCNR、FTEL和POA三种拓扑控制算法运行拓扑,在每轮数据传输过程中,节点均与其邻居节点进行数据交换,节点按照一阶能耗模型计算剩余能量^[12],节点在能量耗尽和拥塞时均按照死亡节点处理,最后统计网络中剩余最大连通分支节点数目,剩余最大连通数目越大表示网络健壮性越好,得到的网络健壮性对比图如图3所示 ...

2010

0.0

2014

0.0

... 综上可知,由于突发数据流引发拥塞后,再采用拥塞控制措施也不一定可以完全避免节点拥塞,很有可能导致节点能量过快耗尽,本文通过理论分析获得了在节点可靠度最大和网络生存时间最长的条件下最优节点度k₀的取值,通过最优节点度约束网络所有节点的节点度,相比目前已有的研究^[10^-^14],根据仅改变最优节点度取值,优化了网络拓扑性能,延长了网络生命周期 ...

2012

0.0

. 2012, 34(9):2180-2186 DOI:doi:10.3724/SP.J.1146.2011.01421

Study on fault tolerant topology of energy heterogeneous wireless sensor networks

能量异构无线传感器网络容错拓扑研究

Yin Rong-rong , Liu Bin , Li Ya-qian

尹荣荣, 刘彬, 李雅倩

Considering the issue of nodes failure for energy heterogeneous wireless sensor networks, a new topology with Adjustable Degree Distribution (ADD) is constructed, and the formulas of degree distribution is obtained. And then through analyzing the effect of degree distribution characteristics on topology tolerance, the optimal topology is derived, which can assure the finish of network monitoring tasks for long under the integrated failure of nodes resulted from energy exhaust and environment damage. The simulation results show that the topology is more robustness, which provides longer lifetime.

该文针对能量异构无线传感器网络中的节点失效问题，提出度分布可调的容错拓扑结构(ADD)，并给出了拓扑的度分布表达式，进而通过解析度分布属性对拓扑容错性的影响，得出在能量耗尽与环境损毁综合节点失效情况下可较长时间维持监测任务的网络拓扑。仿真实验结果表明，新的容错拓扑结构获得了更长的生存时间，具有更好的容错性能。

2014

0.0

. 2014, 63(4):80-86 DOI:doi:10.7498/aps.63.040509

Wireless sensor network fault tolerant topology for lifetime optimization

一种优化传感器无线网络生命周期的容错拓扑研究

Liu Hao-ran , Yin Wen-xiao , Han Tao

刘浩然, 尹文晓, 韩涛

Because of the limited energy of wireless sensor network, the optimization of network lifetime becomes a primary problem in the design of the network. Through analyzing the node residual energy and the load effect on the node lifetime, the fault tolerant topology evolution model in wireless sensor networks is put forward for extending lifetime. And the scope of load adjustment coefficient is obtained under the condition of network survival time. The simulation results show that the topological structure based on the evolution of the scale free network has the good fault tolerance characteristics. And it can also balance the network node energy consumption and the lifetime extension of the network.

由于无线传感器网络的节点能量受限,优化网络生命周期成为设计网络拓扑时首要考虑的问题. 通过分析节点的剩余能量和负载量对节点生命周期的影响,提出了一种可延长无线传感器网络生命期的容错拓扑演化模型,并得出了在节点满足网络生存时间的条件下负载调节系数的取值范围. 仿真实验结果表明,基于无标度网络的演化拓扑结构具有较好的容错性,并能够均衡网络节点能耗和延长网络生命周期.

... 采用一阶无线通信能耗模型^[16],两个相距为d的节点发送l bit数据所消耗的能量E_tx为: ...

... 3 仿真实验与性能分析为了验证TCNR拓扑控制算法的性能,本文采用MATLAB 2012a仿真工具,对具有节能代表性的FTEL算法^[16]和路径优化算法(Path optimization algorithm, POA)^[17]进行仿真实验对比,并且假定拓扑结构均为不分簇的同构平面结构,仿真实验参数见表3 ...

2015

0.0

. 2015, 64(8):080101-

An energy balance topology control algorithm for robustness of wireless sensor networks

一种无线传感器网络健壮性可调的能量均衡拓扑控制算法

Hao Xiao-chen , Liu Wei-jing , Xin Min-jie

郝晓辰, 刘伟静, 辛敏洁