引用本文
谢志强, 郭禾, 苏文秀, 辛宇, 杨静. 存在多工序同时结束的多车间逆序综合调度算法. 2018, 48(2): 578-587
XIE Zhi-qiang, GUO He, SU Wen-xiu, XIN Yu, YANG Jing. Reversal sequence integrated scheduling algorithm of multiple workshop with multi-procedures ended together. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 578-587  
Doi:10.13229/j.cnki.jdxbgxb20160985
Permissions
Copyright©2018, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
存在多工序同时结束的多车间逆序综合调度算法
谢志强1, 郭禾1, 苏文秀1, 辛宇1, 杨静2
1.哈尔滨理工大学 计算机科学与技术学院,哈尔滨 150080
2.哈尔滨工程大学 计算机科学与技术学院,哈尔滨 150001

作者简介:谢志强(1962-),男,教授,博士生导师. 研究方向:企业智能计算与调度优化.E-mail:xiezhiqiang@hrbust.edu.cn

基金项目:国家自然科学基金项目(61370086,61370083,61772160,61602133,61672179); 高等学校博士学科点专项科研基金项目(20122304110012); 黑龙江省教育厅科技项目(12531105); 黑龙江省博士后科研启动项目(LBH-Q13092); 中国博士后科学基金项目(2016M591541); 黑龙江省博士后项目(LBH-Z15096); 全国高等学校计算机教育研究会(研究生创新)项目(ER2014018)
摘要

针对存在多工序同时结束的单件复杂产品的多车间制造问题,提出了存在多工序同时结束的多车间逆序综合调度算法。首先,为解决正序调度需迁移虚拟工序导致的设备资源空闲和操作复杂的问题,设计了逆序分批次调度策略;然后,为减少工序迁移和车间负载尽量均衡,设计了逆序车间确定策略确定所有工序的加工车间;最后,为满足多工序同时结束的特殊约束,设计了逆序同时开始策略确定每组虚拟工序组的逆序开始加工时间。实例验证表明,所提出算法满足特殊约束,完工时间较短且工序迁移次数少。

关键词: 计算机应用; 单件复杂产品; 多车间; 逆序分批次调度策略; 逆序车间确定策略; 逆序同时开始策略
中图分类号:TP278 文献标志码:A 文章编号:1671-5497(2018)02-0578-10
Reversal sequence integrated scheduling algorithm of multiple workshop with multi-procedures ended together
XIE Zhi-qiang1, GUO He1, SU Wen-xiu1, XIN Yu1, YANG Jing2
1. College of Computer Science and Technology, Harbin University of Science and Technology, Harbin 150080,China
2. College of Computer Science and Technology, Harbin Engineering University, Harbin 150001,China
Abstract

To solve the problem in multiple workshop manufacturing that there are single complex products with multi-procedures ended at the same time, a reversal sequence integrated scheduling algorithm is proposed. First, a reverse batch scheduling strategy is designed to solve the problem that migrate virtual processes for positive sequence scheduling can lead to equipment resource idle operating complex. Then, in order to reduce the process migration and keep the balance of load among the workshops, the workshop identified strategy is proposed to assign all the processes to the workshops. Finally, in order to satisfy the special constraints of multi-procedures ended at the same time, a strategy of reversal sequence starting together is designed to determine the reverse starting processing time of each virtual procedure group. A case study verifies that the proposed algorithm meets the special constraints, and the completion time is shortened with less process migrations.

Key words: computer application; single complex products; multiple workshop; reverse batch scheduling strategy; reverse workshop identified strategy; reversal sequence start together strategy
0 引 言

传统产品制造调度问题是纯加工调度和纯装配调度[1, 2, 3], 为解决人们的个性化需求, 文献[4, 5]提出了对单件复杂产品的加工和装配一同处理的综合调度方法。目前的研究成果主要包括一般综合调度问题[6]、柔性综合调度问题[7, 8]、分布式调度研究[9, 10, 11]、多目标调度研究[12, 13, 14]和两车间综合调度问题[15, 16, 17]等。在实际生产过程中, 调度问题经常存在一些特殊的调度约束, 例如, 在火箭的制造过程中, 为了避免某些零件的质量不符合要求, 导致产品无法组装, 影响产品进度, 需要对特殊工序进行匹配度检测后进行调度加工。如文献[18]解决了存在单组多工序同时结束约束的单车间综合调度问题, 为了尽早完工, 采用对虚拟工序单独调度并设计了相关策略, 在多次比较各个虚拟工序的结束时间后迁移虚拟工序, 以满足同时结束的特殊约束, 但其只在理论上进行了简单研究并无实际操作意义与价值。为了进一步提高产品生产效率并且使产品的加工能够一般化, 有必要对存在多工序同时结束的产品进行大众化、一般化的综合调度研究, 以及对存在多组多工序同时结束的单件复杂产品进行多车间综合调度研究。

在产品从单车间到多车间的加工调度过程中, 不仅需要考虑工序迁移和车间负载均衡的问题, 而且需要考虑同时结束的工序中存在相同加工设备的问题。针对正序调度过程需多次迁移虚拟工序造成操作复杂和设备资源浪费的问题, 本文提出存在多工序同时结束的多车间逆序综合调度算法。该算法将多组虚拟工序单独分批次逆序调度, 确定各个批次的调度顺序, 设计逆序车间确定策略来确定每个工序的加工车间, 最后, 采用首次适应调度策略确定一般工序的开始加工时间, 并设计逆序同时开始策略确定每组虚拟工序组的逆序开始加工时间。该算法不仅实现了存在多工序同时结束特殊约束的单件复杂产品从单车间到多车间调度加工的转变, 而且解决了存在特殊约束的多车间调度中产品尽早完工和迁移次数较少的问题。最后, 通过实例调度对本文算法进行了说明分析。

1 问题描述

单件复杂产品在多车间综合调度的过程中, 工序间不仅存在一般的约束关系, 而且部分工序间还存在需要同时结束约束的特殊约束关系。为了使产品的加工和装配尽早完工, 本文设计了逆序调度方法, 将产品虚拟加工树逆序后多车间综合调度的约束关系如下:

(1)在同一时间里, 一道工序只能被一台机器加工且一台机器只能加工一道工序。

(2)每道工序必须在其紧前工序加工完毕后才可加工。

(3)每个车间的各个机器上后续工序需在前续工序加工完毕后开始加工。

(4)有同时结束特殊约束的工序逆序后要求同时开始加工。

(5)每个车间的机器是不完全相同的, 每个工序可选择在哪个车间加工。

(6)每个工序和其紧前工序若不在一个车间加工, 则工序发生一次虚拟迁移。

(7)同组虚拟工序可在多车间中相同设备上加工。

对于一个有N个工序的单件复杂产品在M台机器上加工的问题(其中N个工序中有n组需同时结束的工序, M台设备分布在不同地域的m个不同车间里), 由约束条件分析可知使产品加工尽早完工的数学模型为:

T=min(max(Swij+Twij)) (1)

s.t.min(Swij) (2)

Swi(j+1)≥ Swij+Twij(3)

Sxy≥ Sij+Tij(4)

式中:w表示m个车间中的一个; i=1, 2, …, M; j=1, 2, …, N; Swij为w车间中i设备上第j道工序的开始加工时间; Twij为w车间中i设备上第j道工序的连续加工时间; Sxy为Sij的紧后工序。式(1)表示产品加工时间的目标函数; 式(2)表示每一个工序尽可能早地开始加工; 式(3)表示逆序调度中同一车间同一设备上后续工序需在前续工序加工完毕后开始加工; 式(4)表示逆序调度中紧前工序加工完成后才能加工紧后工序。

由于该问题是多车间逆序加工问题且存在需同时结束的特殊约束条件, 为了缩短工序迁移次数, 保证各个车间的负载均衡, 使产品总的加工时间减少, 需要增加约束条件:

min(V) (5)

min(Tw-Tw') (6)

Swij-Sw'i'j'=0 (7)

式中:V为加工产品的虚拟迁移次数; Tw和Tw'为不同车间上产品工序的总的加工时间; Swij和Sw'i'j'为有同时结束特殊约束的产品工序的逆序开始加工时间。式(5)表示逆序调度过程中工序的虚拟迁移次数尽可能少; 式(6)表示各个车间上工序的总加工时间差尽可能小; 式(7)表示存在同时结束特殊约束的工序逆序同时开始加工。

2 问题分析与策略设计
2.1 问题分析与相关概念

关于存在同时结束特殊工序的问题, 考虑到工序间的特殊约束条件, 若采用正序整体调度的方式, 为保证特殊工序的约束条件需多次移动特殊工序, 导致操作复杂且设备资源空闲。若使用逆序调度策略, 并且将特殊工序单独分离加工, 可避免特殊工序的移动, 达到操作简单且产品完工时间缩短的目的。

关于多车间调度问题, 需要考虑产品的紧前、紧后工序不在同一车间加工产生工序迁移, 导致产品加工出现额外等待的情况, 为了减少产品的完工时间, 必须控制迁移次数。针对多工序同时结束的多车间调度, 相较于单车间, 增加了同组虚拟产品可以存在在多车间相同设备上加工的情况, 需要对多组虚拟工序组的调度多加考虑, 以保证产品在满足特殊约束的情况下完工时间较短。

同时考虑以上问题, 本文设计出一种综合调度算法。为了便于工序按批次进行调度, 工序的属性需要设置为:qi|ei|ti|p|Fq|Lq|wi, 其中qi为工序名, ei为工序qi加工时所用的设备名, ti为工序qi的加工时间, p为特殊工序编号(p=0表示为一般工序, p≠ 0且p值相同表示为同一组需同时结束的特殊工序, p=1, 2, …, n), Fq 为工序qi的紧前工序集, Lq 为工序qi的紧后工序, wi为工序qi加工的车间(wi是通过算法计算得出, 并非已知)。例如:q5|e2|4|2|(q2, q4)|q7|w3表示第2组特殊工序中工序q5在3车间2设备加工4个工时(其中3车间为算法计算得知, 其他为已知), 工序q5的紧前工序有q2和q4, 紧后工序为q7。

分析产品工序的属性信息, 采用逆序调度后, 定义相关概念如下:

定义1 虚拟工序:工序属性中p≠ 0的工序。

定义2 一般工序:工序属性中p=0的工序。

定义3 虚拟工序组p:工序属性中p≠ 0且p值相等的工序。

定义4 虚拟工序组p前续工序:在确定虚拟工序组p后根据工序间约束关系, 循环查找紧前工序直到紧前工序为虚拟工序或紧前工序已定义所得到的所有工序。

定义5 虚拟迁移:加工过程中出现一个逆序紧前工序需要向多个其紧后工序所在加工车间迁移的情况。

设m个车间中设备集合分别为E1, E2, …, Ei, 其中i=1, 2, …, m。定义相关概念如下:

定义6 对称设备资源集Es:在m个车间中共同存在的设备资源构成的集合。即Es=E1∩ E2∩ …∩ Em, 若交集为空, 则无对称资源设备。

定义7 非对称设备资源集Ens:在m个车间中每个车间中单独存在与其他车间无重复的设备的资源构成的集合。即Ens=((E1- E2)∩ (E1- E3)∩ …(E1- Em))∪ ((E2- E1)∩ (E2- E3)∩ …(E2- Em))∪ …∪ ((Em-E1)∩ (Em- E2)∩ …(Em- Em-1))。

定义8 局部对称设备资源集Els:在m个车间中部分车间存在的相同设备资源构成的集合。即Els=(E1∪ E2∪ …∪ Em)- Es-Ens。

2.2 逆序分批次调度策略

由于对存在多工序同时结束的产品采用一般正序调度需要多次调整虚拟工序的开始加工时间, 导致设备资源空闲且加工周期延长。考虑到同时结束的工序逆序调度后只需同时开始即可, 不仅操作简单, 而且避免了工序移动导致的设备资源空闲, 所以本文设计逆序分批次调度策略, 具体步骤如下:

(1)输入产品全部工序的属性信息(不包括工序加工车间信息, 需要计算得知), 将所有工序逆序处理, 即将工序属性信息中紧前工序集与紧后工序信息交换。例如:q5|e2|4|2|(q2, q4)|q7逆序处理后工序属性信息为q5|e2|4|2|q7|(q2, q4), 表示虚拟工序组2中工序q5在2设备加工4个工时, 工序q5的紧前工序为q7, 紧后工序有q2和q4。

(2)遍历工序属性信息, 得到p=1时的所有工序, 即虚拟工序组1, 将虚拟工序组1单独划分。根据虚拟工序组1中工序属性信息和定义4确定虚拟工序组1前续工序, 并将其单独划分。得到虚拟工序组1和虚拟工序组1前续工序。

(3)遍历工序信息, 依次得到虚拟工序组p和虚拟工序组p 前续工序, 其中p=1, 2, …, n。

(4)将虚拟工序组p和虚拟工序组p前续工序划分为2n部分完毕后, 剩余的工序划分为单独的一部分, 共得到2n+1的独立部分工序集。

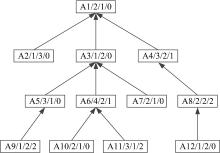
为方便理解, 特举例说明逆序分批次调度策略。例如图1所示的产品A, 方框内产品工序属性信息表示为:工序名/加工设备名/加工时间/是否虚拟工序。逆序分批次调度策略的具体过程如下:将产品A的虚拟加工工艺树中所有工序的紧前、紧后关系取反; 遍历虚拟加工工艺树, 得到p=1的工序为A4和A6; 根据定义4查找得到虚拟工序A4和A6的前续工序集为{A1, A3}; 遍历虚拟加工工艺树, 得到p=2的工序为A8、A9和A11; 根据定义4查找得到虚拟工序A8、A9和A11的前续工序集为{A5}; 最后剩余工序为A2, A7, A10, A12。因为产品A中有2组虚拟工序组, 所以最后分批次得到5部分工序集, 见表1。

图1 产品A的加工工艺树Fig.1 Process tree of product A

表1 产品A逆序分批次调度结果 Table 1 Reverse batch scheduling result of product A
2.3 确定工序调度顺序

单件复杂产品的虚拟工艺树中都存在一条关键路径, 优先加工关键路径上的工序可以使产品横向上工序能更好地并行调度, 而且使产品纵向上的后序工序可以更多地与其他工序并行调度, 故本文采用逆序动态关键路径调度策略。当动态关键路径策略不能确定工序调度顺序时, 即有两个或多个工序有相同的路径长度时, 优先加工用时较短的工序, 可以使后续工序获得较早的加工时间, 使后续工序充分并行调度, 所以本文同时采用逆序短用时策略。

对存在多工序同时结束的单件复杂产品, 在设计逆序分批次调度策略后, 考虑到虚拟工序组p前续工序和剩余工序为多个虚拟的加工工艺树, 故采用上述策略确定各个部分的调度顺序, 以确保工序间的并行调度和缩短各部分虚拟产品的完工时间。而虚拟工序组p是存在同时结束特殊要求的工序, 即逆序后要求同时开始加工的工序, 若多车间中同组虚拟工序存在加工设备相同的情况, 则其不能在同一车间加工, 增加了虚拟工序车间确定的复杂性, 每组虚拟工序组的调度顺序可随机。对图1中产品A虚拟加工树设计逆序分批次调度策略后, 确定调度顺序见表2。

表2 产品A各部分调度顺序 Table 2 Scheduling order of parts of product A
2.4 逆序车间确定策略

对单件复杂产品的工序属性信息分析可知, 可以构造一个虚拟的树状产品加工工艺树, 所有的叶子节点工序的属性信息无紧前工序, 根节点工序无紧后工序, 其余节点工序属性信息中有一个或多个紧前工序, 有且仅有一个紧后工序。设计逆序分批次调度策略后, 各个工序属性信息发生变化, 原工序属性信息中紧前工序集变为逆序后工序属性信息中的紧后工序集, 原工序属性信息中的紧后工序变为逆序后工序属性信息中的紧前工序, 根节点工序无紧前工序, 所有叶子节点工序无紧后工序。分析m个车间中M台设备的属性, 判断M台设备分别为对称设备资源集Es、非对称设备资源集Ens、局部对称设备资源集Els。

为了保证产品生产周期尽可能短, 需要考虑产品工序在车间之间的迁移尽量少; 为了使产品工序充分的并行调度, 需要使各个车间的负载尽量均衡。考虑到以上因素, 设计逆序车间确定策略, 设虚拟迁移数用Vr=0表示, 具体步骤如下:

(1)输入产品工序信息, 设计逆序分批次调度策略确定各部分调度工序, 然后确定各部分工序的调度顺序。

(2)按调度顺序取出工序, 判断该工序所需加工设备, 若属于非对称设备资源集Ens, 则将该工序放入非对称设备所在车间加工, 继续判断该工序紧前工序所在车间, 若为同一车间则工序虚拟迁移数Vr不变, 转步骤(8); 若不在同一车间, 则虚拟迁移数Vr++, 转步骤(8)。

(3)若该工序所需加工设备属于局部对称设备资源集Els, 继续判断该工序紧前工序所加工车间能否加工该工序(其中包括该工序紧前工序加工车间有无该工序加工设备和该工序紧前工序加工车间的该工序加工设备是否已加工与该工序同组的虚拟工序), 若能, 转步骤(4), 若不能, 转步骤(5); 否则, 转步骤(6)。

(4)确定该工序在其紧前工序所在加工车间加工, 转步骤(7)。

(5)为保证车间负载均衡选择加工时间少的车间调整加工该工序且虚拟迁移数Vr++, 转步骤(8)。

(6)若该工序所需加工设备属于对称设备资源集Es, 转步骤(4); 否则转步骤(7)。

(7)若该工序为一般工序, 转步骤(8); 否则判断该工序加工设备是否已加工同组虚拟工序, 若已加工, 则转步骤(5), 否则转步骤(8)。

(8)所有工序确定完毕则结束, 否则转步骤(2)。

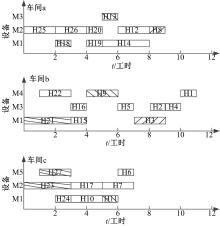
为方便理解, 对图1所示产品A采用逆序车间确定策略确定所有工序加工车间, 设有3个车间, 车间a有设备M1、M2、M4, 车间b有设备M1、M2, 车间c有设备M1、M3。由定义6、定义7和定义8可知, M1属于对称设备资源集Es, M2属于局部对称设备资源集Els, M3和M4属于非对称设备资源集Ens。

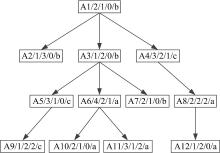
按A1, A3, A4, A6, A5, A8, A9, A11, A2, A12, A7, A10顺序依次取出工序确定车间, 工序A1需在设备M2上加工, M2∈ Els, 因为A1是根节点工序, 逆序无紧前工序, 可任选一车间a或b加工, 选择车间b加工; 工序A3需在设备M1上加工, M1∈ Es, 工序A3的紧前工序A1在车间b加工, 故A3在车间b加工且Vr=0; 工序A4需在设备M3上加工, M3∈ Ens, 确定工序A4在车间c加工, 工序A4的紧前工序A1在车间b加工, 故Vr=1; 以后各个工序处理方式相同, 最后得到产品A的工序属性如图2所示, 虚拟迁移数Vr=4。

图2 确定产品A工序加工车间Fig.2 Determine machining workshop of the product A

2.5 逆序同时开始策略

通过以上策略设计与应用, 确定了2n+1个部分工序集和所有工序的加工车间属性, 针对n个虚拟工序组p前续工序组成的各部分工序集和剩余工序组成的工序集, 为保证一般工序能够在其车间设备上尽早开始加工, 可使用首次适应调度策略[5]确定一般工序的开始加工时间, 而针对n组虚拟工序组p, 为满足其同时结束的特殊约束, 本文设计逆序同时开始策略确定虚拟工序的开始加工时间, 具体步骤如下:对n组虚拟工序组p(p=1, 2, …, n); 从虚拟工序组1开始, 查找虚拟工序组1中工序的逆序紧前工序, 比较各个紧前工序在其加工车间的结束加工时间, 得到最晚的结束加工时间, 以此时间点为虚拟工序组1中所有虚拟工序的开始加工时间; 重复以上步骤, 直到n组虚拟工序组p全部确定开始加工时间。

图1所示产品A虚拟加工工艺树, 确定调度顺序为A1, A3, A4, A6, A5, A8, A9, A11, A2, A12, A7, A10, 按序确定开始加工时间, A1开始加工时间为0, A3开始加工时间为1, A4和A6的开始加工时间为3, 全部工序得到开始加工时间后则产品加工完毕。

3 算法详细设计

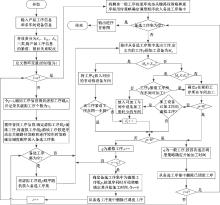
根据以上分析和策略设计, 为了实现存在多工序同时结束的多车间综合调度目标, 算法流程图如图3所示, 算法的具体步骤如下:

(1)输入产品工序信息和多车间设备信息。

(2)根据定义6、定义7、定义8确定对称设备资源集Es、非对称设备资源集Ens、局部对称设备资源集Els; 按逆序分批次调度策略将产品工序紧前、紧后关系取反; 定义循环变量i=1。

(3)若i> n, 转步骤(21); 否则转步骤(4)。

(4)令工序属性p=i, 遍历工艺树得到虚拟工序组p, 并记录其虚拟工序个数为vp。

(5)根据定义4确定虚拟工序组p前续工序, 并按逆序动态关键路径策略和逆序短用时策略确定调度顺序加入备选工序集。

(6)若备选工序集为空, 转步骤(7); 不为空则转步骤(8)。

(7)将虚拟工序组p随机加入备选工序集。

(8)按序从备选工序集中选出工序, 定义当前工序q的加工设备为Eq。

(9)若Mq∈ Ens, 将工序q放入对应的车间设备加工; 否则转步骤(11)。

(10)若工序q的紧前工序和工序q在同一车间加工, 转步骤(17); 否则转步骤(14)。

(11)若Mq∈ Els, 转步骤(12); 否则转步骤(15)。

(12)若工序q紧前工序所在车间可加工工序q, 则转步骤(15); 否则转步骤(13)。

(13)调整放入可加工车间中加工用时少的车间加工工序q。

(14)虚拟迁移数Vr++, 转步骤(17)。

(15)确定工序q在其紧前工序所在车间加工。

(16)若工序q的属性p=0, 则转步骤(17);

否则判断工序q的加工设备是否已加工同组虚拟工序, 若是则转步骤(13), 若不是则转步骤(17)。

图3 算法流程图Fig.3 Flow chart of algorithm

(17)若工序q的属性p=0, 则工序q为一般工序, 按首次适应调度策略确定工序q的开始加工时间, 从备选工序集中删除已调度工序, 转步骤(20); 否则工序q为虚拟工序, v++, 转步骤(18)。

(18)若v=vp, 表示备选工序集中工序全部确定加工车间, 转步骤(19); 否则转步骤(8)。

(19)确定备选工序集中为虚拟工序组p, 按逆序同时开始策略确定开始加工时间, 令v=0, 从备选工序集中删除已调度工序, i++, 转步骤(3)。

(20)若i> n, 则转步骤(22); 否则转步骤(6)。

(21)将剩余一般工序按逆序动态关键路径策略和逆序短用时策略确定调度顺序并放入备选工序集中。

(22)若备选工序集为空, 转步骤(23); 不为空则转步骤(8)。

(23)输出逆序调度甘特图, 结束。

4 算法复杂度分析

设产品共有N个工序, 其中有n组虚拟工序(n组虚拟工序组共有Nn个虚拟工序), 在m间车间中的M台设备上加工, 设n组虚拟工序组工序数为x1, x2, …, xn, x1+x2+…+xn=Nn。n组虚拟工序组前续工序个数为y1, y2, …, yn, 分析如下:

(1)逆序分批次调度策略:将N道工序中的紧前、紧后关系取反, 需要N次操作, 逆序操作时间复杂度为O(N); 遍历加工工艺树, 确定虚拟工序组1需要x1次, 确定虚拟工序组1前续工序需要y1次, 直到确定虚拟工序组n需要xn次, 确定虚拟工序组n前续工序需要yn次, 确定2n+1部分需要每个节点访问一次, 故时间复杂度为O(N)。

(2)逆序动态关键路径策略和逆序短用时策略:根据文献[5], 对N-Nn个一般工序确定调度顺序的比较次数为(N-Nn)( N-Nn-1), 故时间复杂度为O(N)2。

(3)逆序车间确定策略:根据定义6、定义7、定义8确定设备种类Es、Ens和Els个数分别为h1、h2和h3, 由于工序加工设备已知, 判断设备属于非对称设备资源集最多需要h1次, 然后确定工序紧前工序是否在同一车间需比较1次, 于是确定加工设备为非对称设备资源集设备的工序确定加工车间需要判断h1+1次。判断工序加工设备属于局部对称设备资源集最多需要h2次, 确定紧前工序所在车间不可加工该工序最多需判断M次, 判断虚拟迁移1次, 于是确定加工设备为局部对称设备资源集设备的工序确定加工车间需要判断h2M+1次。判断工序加工设备属于对称设备资源集最多需要h3次, 确定紧前工序所在车间加工需操作1次, 于是确定加工设备为对称设备资源集设备的工序确定加工车间需要判断h3+1次。因此, N个工序全部确定加工车间最坏需要N(h2M+1)次操作, h2< M, 故时间复杂度为O(NM2)。

(4)确定开始加工时间:对N-Nn个一般工序, 根据文献[5]采用首次适应调度策略确定开始加工时间复杂度为O(N-Nn)2; 对于虚拟工序组n, 得到每个虚拟工序紧前工序结束时间需操作xn次, 判断最晚结束时间需xn-1次, 确定虚拟工序组n开始加工时间2xn-1次。故确定Nn个虚拟工序的开始加工时间需操作(2x1-1)+(2x2-1)+ …+(2xn-1)=2Nn-n次, 时间复杂度为O(N)。

由上述分析可知, 存在多工序同时结束的多车间逆序综合调度算法的时间复杂度不超过3次多项式。

5 实例分析与对比
5.1 调度实例

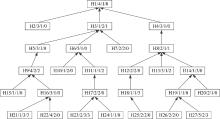
上述算法设计目的具有普遍意义, 不以具体实例为对象, 而为了帮助读者进一步理解, 本文以图4为例做详细说明。

对图4所示产品H虚拟加工树进行多车间调度, 设有3个车间, 分别是a车间、b车间、c车间, 其中a车间有设备M1、M2和M3; b车间有设备M1、M3和M4; c车间有设备M1、M2和M5。根据定义6、定义7和定义8分析3个车间信息可得, 对称设备资源集Es为{M1}, 非对称设备资源集Ens为{M4, M5}, 局部对称设备资源集Els为{M2, M3}。

调度产品H的具体过程如下:

首先, 将各个工序间约束关系取反, 根据工序属性确定虚拟工序组1为{H3, H8}, 根据定义4确定虚拟工序组1前续工序为{H1, H4}; 依次确定虚拟工序组2为{H9, H11, H13}, 虚拟工序组2前续工序为{H5, H6}, 虚拟工序组3为{H18, H21, H23, H27}, 虚拟工序组3前续工序为{H12, H14, H16, H17, H19}, 剩余工序为{H2, H7, H10, H15, H20, H22, H24, H25, H26}。

图4 产品H加工工艺树Fig.4 Process tree of product H

然后, 将虚拟工序组1前续工序按逆序动态关键路径策略和逆序短用时策略确定调度顺序为{H1, H4}, 依次确定工序加工车间, 工序H1需加工设备为M4, M4为非对称设备资源集Ens中设备, 确定H1在车间b加工, 无紧前工序不存在虚拟迁移, 按首次适应调度策略确定开始加工时间为0; 工序H4需加工设备为M3, M3为局部对称设备资源集Els中设备, H4紧前工序为H1在车间b加工, 该车间可加工H4, 确定H4在车间b加工, 无虚拟迁移, 按首次适应调度策略确定开始加工时间为1。将虚拟工序组1{H3, H8}中工序确定加工车间, 工序H3需加工设备为M1, M1为对称设备资源集Es中设备, H3紧前工序H1在车间b加工, 确定H3在车间b加工; 工序H8需加工设备为M2, M2为局部对称设备资源集Els中设备, H8紧前工序为H4在车间b加工, 该车间不可加工工序H8, 计算M2所在车间a和车间c加工用时相等, 故可任选一车间调度, 确定H8在车间a加工, H8存在虚拟迁移, Vr=Vr+1; 得到H3和H8的紧前工序H1和H4的加工结束时间为1和2, 按逆序同时开始策略确定虚拟工序组1的开始加工时间为2。

重复上述步骤依次确定, 虚拟工序组2前续工序的调度顺序为{H6, H5}, 加工车间分别为车间c和车间b, 开始加工时间均为4; 虚拟工序组2为{H9, H11, H13}, 加工车间依次分别为车间b、车间c和车间a, 开始加工时间均为5; 虚拟工序组3前续工序的调度顺序为{H12, H14, H17, H16, H19}, 加工车间分别为车间a、车间a、车间c、车间b和车间a, 开始加工时间分别为3、3、6、7和6; 虚拟工序组3为{H18, H21, H23, H27}, 加工车间分别为车间a、车间b、车间c和车间c, 开始加工时间均为8。

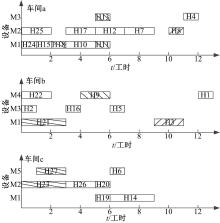
最后, 确定剩余工序的调度顺序为{H7, H10, H22, H25, H26, H2, H15, H20, H24}, 加工车间分别为车间c、车间c、车间b、车间a、车间a、车间b、车间b、车间a和车间c, 开始加工时间依次分别为4、6、8、7、5、2、7、6和8。图5为根据逆序调度结果确定的正序调度甘特图, 可知产品完工时间为11工时。由算法调度过程可知, 产品工序间的虚拟迁移次数是5次。

图5 产品H的调度甘特图Fig.5 Gantt chart of product H

5.2 对比分析

为了充分说明本文算法较优, 下面介绍基于正序调度的算法。其主要思想与逆序调度的区别在车间确定和虚拟工序组开始加工时间。其中, 确定车间策略是:判定该工序加工设备是否属于Ens, 若是, 则确定该工序放入对应的非对称设备车间, 判断该工序和其紧前工序加工车间确定Vr; 若不是, 则继续判定该工序加工设备是否属于Els, 若是, 则按该工序紧前工序加工车间从多到少依次判断可加工即放入该车间加工, 不可加工则放入对应可加工车间加工并判断Vr; 若不是, 则该工序加工设备属于Es, 放入其紧前工序加工车间最多的车间加工, 若无紧前工序或无法通过紧前工序加工车间确定则根据车间均衡选择加工车间加工。每组虚拟工序组的开始加工时间调度策略可参考文献[18]。最后, 调度文本实例得到甘特图, 如图6所示。

图6 对比算法调度结果甘特图Fig.6 Gantt chart of scheduling result by using contrast algorithm

将图5与图6对比可以看出, 采用本文算法产品完成时间为11工时, 迁移次数为5次, 采用基于正序的调度算法的产品完成时间为13工时, 迁移次数为8次。之所以本文算法效果更好, 是因为逆序调度可以更好地设计多组多工序逆序同时开始, 减少设备资源空闲和调整工序, 使操作更加简单实用, 并且逆序调度比正序调度车间确定策略更容易实现, 减少了工序的迁移。

6 结 论

(1)逆序分批次调度策略减少了整体调度产生的设备资源占用问题。

(2)逆序车间确定策略确定所有工序加工车间, 减少了工序间的迁移。

(3)逆序同时开始策略简单方便地实现了工序间的特殊约束, 减少了工序调整。

The authors have declared that no competing interests exist.

参考文献
[1] 李京生, 王爱民, 唐承统, 等. 基于动态资源能力服务的分布式协同调度技术[J]. 计算机集成制造系统, 2012, 18(7): 1563-1574.
Li Jing-sheng, Wang Ai-min, Tang Cheng-tong, et al. Distributed coordination scheduling technology based on dynamic manufacturing ability service[J]. Computer Integrated Manufacturing Systems, 2012, 18(7): 1563-1574. [本文引用:1]
[2] 周鑫, 马跃, 胡毅. 求解车间作业调度问题的混合遗传模拟退火算法[J]. 小型微型计算机系统, 2015, 36(2): 370-374.
Zhou Xin, Ma Yue, Hu Yi. Mixed genetic algorithm and simulated annealing algorithm for solving job shop scheduling problem[J]. Journal of Chinese Computer Systems, 2015, 36(2): 370-374. [本文引用:1]
[3] 叶寒锋, 李占山, 陈超. 基于具有自适应与自学习能力的粒子群优化算法的车间调度算法[J]. 吉林大学学报: 理学版, 2014, 52(1): 93-97.
Ye Han-feng, Li Zhan-shan, Chen Chao. Adaptive and self-learning pso-based algorithm for job shop scheduling problem[J]. Journal of Jilin University(Science Edition), 2014, 52(1): 93-97. [本文引用:1]
[4] 赵诗奎, 方水良. 基于工序编码和邻域搜索策略的遗传算法优化作业车间调度[J]. 机械工程学报, 2013, 49(16): 160-169.
Zhao Shi-kui, Fang Shui-liang. Operation-based encoding and neighborhood search genetic algorithm for job shop scheduling optimization[J]. Journal of Mechanical Engineering, 2013, 49(16): 160-169. [本文引用:1]
[5] 谢志强, 杨静, 周勇, 等. 基于工序集的动态关键路径多产品制造调度算法[J]. 计算机学报, 2011, 34(2): 406-412.
Xie Zhi-qiang, Yang Jing, Zhou Yong, et al. Dynamic critical paths multi-product manufacturing scheduling algorithm based on operation set[J]. Chinese Journal of Computers, 2011, 34(2): 406-412. [本文引用:1]
[6] 曾强, 杨育, 王小磊, 等. 基于多规则设备分配及工序排序的FJSP多目标集成优化方[J]. 计算机集成制造系统, 2011, 17(5): 980-989.
Zeng Qiang, Yang Yu, Wang Xiao-lei, et al. Integrated multi-objective optimization method for FJSP based on multiple rule machine assignment and job sequencing[J]. Computer Integrated Manufacturing Systems, 2011, 17(5): 980-989. [本文引用:1]
[7] 谢志强, 桂忠艳, 杨静. 基于设备驱动和实质路径的动态并行综合柔性调度算法[J]. 机械工程学报, 2014, 50(18): 204-211.
Xie Zhi-qiang, Gui Zhong-yan, Yang Jing. Dynamic parallel integrated flexible scheduling algorithm based on device driver and essential path[J]. Journal of Mechanical Engineering, 2014, 50(18): 204-211. [本文引用:1]
[8] 谢志强, 周含笑, 于洁, 等. 基于设备驱动的综合柔性调度冲突调解算法[J]. 北京理工大学学报, 2014, 34(11): 1151-1156.
Xie Zhi-qiang, Zhou Han-xiao, Yu Jie, et al. Conflict mediation algorithm of the integrated flexible scheduling based on the device driver[J]. Transactions of Beijing Institute of Technology, 2014, 34(11): 1151-1156. [本文引用:1]
[9] Palmieri F, Buonanno L, Venticinque S, et al. A distributed scheduling framework based on selfish autonomous agents for federated cloud environments[J]. Future Generation Computer Systems, 2013, 29(6): 1461-1472. [本文引用:1]
[10] Oike S, Tanaka T, Zhu J, et al. Robust production scheduling using autonomous distributed systems[J]. Key Engineering Materials, 2012, 516: 166-169. [本文引用:1]
[11] Valilai O F, Houshmand M, et al. A collaborative and integrated platform to support distributed manufacturing system using a service-oriented approach based on cloud computing paradigm[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(1): 110-127. [本文引用:1]
[12] 陶辛阳, 夏唐斌, 奚立峰. 基于健康指数的预防性维护与多目标生产调度联合优化建模[J]. 上海交通大学学报, 2014, 48(8): 1170-1174.
Tao Xin-yang, Xia Tang-bin, Xi Li-feng. Health-index-based joint optimization of preventive maintenance and multi-attribute production scheduling[J]. Journal of Shanghai Jiaotong University, 2014, 48(8): 1170-1174. [本文引用:1]
[13] Dalfard V M, Mohammadi G. Two meta-heuristic algorithms for solving multi-objective flexible job-shop scheduling with parallel machine and maintenance constraints[J]. Computers & Mathematics with Applications, 2012, 64(6): 2111-2117. [本文引用:1]
[14] Marichelvam M K, Prabaharan T, Yang X S. A discrete firefly algorithm for the multi-objective hybrid flowshop scheduling problems[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(2): 301-305. [本文引用:1]
[15] 谢志强, 周含笑, 桂忠艳, 等. 基于拟关键路径的二车间综合调度算法[J]. 计算机科学, 2013, 40(4): 193-198.
Xie Zhi-qiang, Zhou Han-xiao, Gui Zhong-yan, et al. Integrated scheduling algorithm of two workshops based on ACPM[J]. Computer Science, 2013, 40(4): 193-198. [本文引用:1]
[16] 谢志强, 郑付萍, 朱天浩. 两车间可调度工序均衡处理的综合调度算法[J]. 计算机工程, 2014, 40(1): 295-304.
Xie Zhi-qiang, Zheng Fu-ping, Zhu Tian-hao. Integrated scheduling algorithm with equalization processing of schedulable processes in two workshops[J]. Computer Engineering, 2014, 40(1): 295-304. [本文引用:1]
[17] 谢志强, 于洁, 陈德运, 等. 基于邻域渲染的二车间综合调度算法[J]. 机械工程学报, 2016, 52(1): 149-159.
Xie Zhi-qiang, Yu Jie, Chen De-yun, et al. Integrated scheduling algorithm of two workshops based on the principle of the neighborhood rendering[J]. Journal of Mechanical Engineering, 2016, 52(1): 149-159. [本文引用:1]
[18] 朱天浩, 谢志强, 郑付萍. 存在多工序同时结束的综合调度算法[J]. 计算机应用研究, 2013, 30(10): 2907-2911, 2919.
Zhu Tian-hao, Xie Zhi-qiang, Zheng Fu-ping. Integrated scheduling algorithm of multi-procedures ended together[J]. Application Research of Computers, 2013, 30(10): 2907-2911, 2919. [本文引用:1]