基于新型线边集成超市的周期性物料配送优化

引用本文

周炳海, 徐佳惠, 彭涛. 基于新型线边集成超市的周期性物料配送优化. 2018, 48(2): 588-595
ZHOU Bing-hai, XU Jia-hui, PENG Tao. Optimization of cyclic part feeding with novel line-integrated supermarket. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 588-595 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161370
Permissions

基于新型线边集成超市的周期性物料配送优化

周炳海, 徐佳惠, 彭涛

同济大学机械与能源工程学院,上海 201804

作者简介:周炳海(1965-),男,教授,博士生导师.研究方向:制造系统调度、建模与仿真.E-mail:bhzhou@tongji.edu.cn

基金项目:国家自然科学基金项目(71471135)

摘要

为结合传统线边储料和成套供料的优势,有效改善汽车混流装配线的送料机制,引入一种新型线边集成超市物料配送系统,并对送料工人进行物料配送工位分配和周期性配送优化。首先,对相互关联的工位分配和周期性配送问题进行描述,并以最小化送料工人固定成本和物料配送成本为目标建立数学模型。其次,结合模型提出引理定理、构建嵌套启发式动态规划方法获取小规模问题的精确解,对于中大规模问题,构建改进型和声搜索算法进行求解。在算法设计中,通过反复拆分、合并和声记忆库加快算法的搜索速度,并融入邻域搜索、交叉变异等操作以扩大和声搜索空间、避免传统和声搜索算法早熟收敛、易陷入局部最优等缺点。最后,通过仿真实验与其他改进算法进行对比,验证了该算法运行速度快、搜索结果优,可有效解决物料配送优化问题。

关键词: 计算机应用; 物料配送; 线边集成超市; 周期性配送; 动态规划; 和声搜索算法

中图分类号:TP29 文献标志码:A 文章编号:1671-5497(2018)02-0588-08

Optimization of cyclic part feeding with novel line-integrated supermarket

ZHOU Bing-hai, XU Jia-hui, PENG Tao

School of Mechanical Engineering, Tongji University, Shanghai 201804, China

Abstract

To combine the advantages of line stocking and kitting, a novel line-integrated supermarket model was proposed to further improve the part feeding process in mixed-model assembly lines, and the task assignment of logistic workers and part feeding period were optimized. First, the interdependent task assignment and cyclic part feeding problems were described. The mathematical models were built to minimize the total cost of logistic workers hiring and parts delivering. Then, based on the theorems, the dynamic programming embedded with heuristics was adopted to obtain the optimum for small scale problems. For medium and large-scale problems, a Modified Harmony Search Algorithm (MHSA) was constructed to generate satisfactory solutions. To accelerate the searching process, the harmony memory was repeatedly divided and regrouped. A local search method, crossover and mutation were employed to explore the searching space, thus to overcome the deficiencies of the original algorithm, such as limited search depth and the tendency to trap into local optimum. Finally, simulation of the modified algorithm was carried out and the results were compared with that of other evolution algorithms. The rapid operation speed and effectiveness of the proposed method were verified.

Key words: computer application; part feeding; line-integrated supermarkets; cyclic delivery; dynamic programming; harmony search algorithm

Show Figures

0 引言

物料配送(Part feeding)占车辆生产成本的20%~50%^[1]。如何设计高效、合理的物料配送系统, 对降低混流装配线的生产成本具有重要意义。

许多国内外学者对传统送料机制, 即线边储料(Line stocking)和成套供料(Kitting)进行了广泛的对比和研究^{[2, 3]}, 并指出不存在绝对的最优机制, 应根据物料特性和实际生产环境选用不同送料机制才可有效降低系统配送总成本。近年来, 研究焦点逐渐转移为准时化配送策略^{[4, 5]}, 即采用物料超市(Supermarket)替代传统的中心仓库存放物料, 通过对多载量小车等送料设备的调度^[6]实现物料的小批量多频次配送。为充分结合传统线边储料、成套供料以及准时化配送策略的优势, 降低系统总运作成本, Boysen等^[7]结合某德国汽车制造商的实际运营情况, 提出并介绍了“ 线边集成超市” (Line-integrated supermarkets)的概念, 但未对具体的物料配送调度问题进行深入研究。Battini等^[8]对厂内物流进行研究时也简单提及了“ 鱼骨型物流超市” (Fish bone supermarkets), 即线边集成超市, 并说明了其可行性和潜在价值。

虽然基于线边集成超市的物料配送有效利用当前送料机制的优势、降低系统成本, 但是目前尚未发现其他相关研究。为此, 本文引入线边集成超市的概念, 研究送料工人与工位之间的合理配置问题, 并对物料配送进行调度决策, 以最小化包括工人固定成本和物料配送成本的系统总运作成本。对于小规模问题, 结合问题的引理、定理建立嵌套启发式动态规划方法获取精确解, 并构建改进型和声搜索算法(Modified harmony search algorithm, MHSA)求中大规模问题的满意解。

1 问题描述

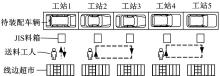
如图1所示, 为有效降低物料的线边库存, 送料工人采用准时化顺序供应(Just-in-sequence, JIS), 即根据实际生产计划和装配情况准备并配送物料到对应工位, 并按需按序放置于JIS料箱, 以满足装配需求。为明确物料配送任务、有效管理送料工人, 本文将物料配送调度分解成两个子问题:①送料工人与工位的分配问题P₁, 即确定各送料工人负责工位; ②周期性配送问题P₂, 即确定送料工人的周期性配送时间间隔。

	Figure Option View Download New Window
	图1 线边集成超市物料配送系统Fig.1 Part feeding system with line-integrated supermarkets

为有效描述该配送系统, 作如下假设:①采用节拍时间作为基本时间单位; ②装配线不允许发生缺料; ③一个送料工人负责一个或多个连续工位; ④送料工人对所负责的工位进行周期性配送; ⑤送料工人搬运能力有限; ⑥送料工人一旦从线边超市出发送料, 必须配送完所有物料后返回; ⑦每个工位设一个JIS料箱, 存放物料, 其容量有限; ⑧送料工人拣料、卸料时间, 以及从线边超市到工位的行走时间均为定值; ⑨每个工位仅装配一类物料, 且仅考虑每个生产节拍内的物料需求量; ⑩生产系统为一个相对稳定的系统, 不考虑不确定因素。

结合以上描述和假设, 定义如下问题参数和决策变量, 并建立数学模型。

(1)参数与变量

设S为装配工位集合, s=1, 2, …, ; W为送料工人集合, w=1, 2, …, ; P为待装配车辆总数, p=1, 2, …, P; T为系统生产节拍总数, t=1, 2, …, T; ct为系统节拍时间; B_s为工位s处JIS料箱的容量; 为工位s在第t个生产节拍所需物料量; wt为送料工人从线边超市到工位的行走时间; st为送料工人在两连续工位间的行走时间; at_w为送料工人w每次的分拣、装卸物料时间; C_w为第w个送料工人的搬运能力; δ _w为第w个送料工人负责的最左边工位编号; T_w为第w个送料工人的周期性配送时间间隔, 且T_w≥ 1; D_w为第w个送料工人的单次送料时长, 且D_w=at_w+2· [wt+st· (δ _w+₁-1-δ _w)]; R_w为第w个送料工人的送料次数, r=1, 2, …, R_w; 为第w个送料工人第r次配送的物料量; F_w为第w个送料工人的固定成本; u为单位物料单位时间的搬运成本。

(2)数学模型

P₁:Z₁=min (1)

s.t. δ ₁=1(2)

δ _w+₁-1≥ δ _w, ∀ w∈ W (3)

$\begin{matrix} δ_{|W| + 1} \end{matrix}$ =+1 (4)

式(1)~(4)以最小化送料工人数为目标求解问题P₁。其中, 式(2)(3)表示各送料工人至少负责1个工位, 且负责的工位不重复。式(4)为终止条件, +1和+1均为虚拟值, 不计入目标函数。此外, 为有效应对问题P₂, 即减少物料配送等非增值活动的成本, 建立以最小化单位物料配送的最大时间为目标的数学模型, 如式(5)所示。式(6)(7)为配送量约束, 即应满足装配过程不发生缺料。式(8)(9)分别为送料工人能力和JIS料箱容量约束。式(10)表明送料工人周期性配送时间间隔不得小于其固定的送料时长。

P₂:minZ₂(T_w)=max $\begin{matrix} \frac{1}{R_{w}} \end{matrix} \begin{matrix} \overset{R_{w}}{\sum_{r = 1}} \end{matrix} \begin{matrix} \frac{D_{w}}{Q_{r}^{w}} \end{matrix}$ (5)

s.t. = $\begin{matrix} \overset{δ_{w + 1} - 1}{\sum_{s = δ_{w}}} \end{matrix}$ $\begin{matrix} \overset{(r + 1) \cdot T_{w} / ct}{\sum_{t = r \cdot T_{w} / ct}} \end{matrix}$ (6)

∀ w∈ W; s∈ S; r=1, 2, …, R_w

$\begin{matrix} \overset{R_{w}}{\sum_{r = 1}} \end{matrix}$ = $\begin{matrix} \overset{δ_{w + 1} - 1}{\sum_{s = δ_{w}}} \end{matrix} \begin{matrix} \overset{T}{\sum_{t = 1}} \end{matrix}$ (7)

∀ w∈ W; s∈ S; r=1, 2, …, R_w

≤ C_w, ∀ w∈ W; r=1, 2, …, R_w(8)

$\begin{matrix} \overset{(r + 1) \cdot T_{w} / ct}{\sum_{t = r \cdot T_{w} / ct}} \end{matrix}$ ≤ B_s(9)

∀ w∈ W; s∈ S; r=1, 2, …, R_w

D_w≤ T_w, ∀ w∈ W(10)

显然, 两个子问题相互关联:工位分配问题确定送料工人数和负责工位(W, δ _w), 其作为问题P₂的已知参数; 相应地, 只有求出每个工人的周期性配送时间才可明确工人数是否满足要求, 工位分配问题是否合理、可行。基于两者的关联性, 结合式(1)(5)建立总目标函数(11)进行求解, 其代表最小化包括工人固定成本和物料配送成本的系统总成本, 式中“ * ” 表示相应目标函数的最优解。函数(11)应满足约束(2)(3)(4)、(6)~(10)。

Z=minZ₁· F_w+u· $\begin{matrix} [\overset{R_{w}}{\sum_{r = 1}} Q_{r}^{w} \cdot Z_{2}^{*} (T_{w})] \end{matrix}$ (11)

2 算法构建

2.1 引理和定理

定理1 若S、T、、C_w已知, 则当∀ w∈ W, T_w=1, 且∀ t=1, 2, …, T, Φ =max时, 则可得 $\begin{matrix} {|W|}_{\min} \end{matrix}$ =「Φ /C_w⌉。

证明根据约束(7), 可得 $\sum_{w}^{\in} \overset{R_{w}}{\sum_{r = 1}}$ = $\sum_{s} \begin{matrix} \overset{T}{\sum_{t = 1}} \end{matrix}$ 。则∀ w∈ W, T_w=1时, R_w=「T/T_w⌉=T, 即:∀ r=t=1, 2, …, T, $\sum_{s}^{\in} d_{s}^{t}$ = $\sum_{w}^{\in} Q_{r}^{w}$ 。由假设②和约束(8)可知, 为满足装配线物料需求, 送料工人数必须满足任何生产节拍时所有工位的物料需求, 故最小值 $\begin{matrix} {|W|}_{\min} \end{matrix}$ =「max/C_w⌉, 即定理1得证。

引理1 若送料工人w负责工位m, …, n的物料配送, 且周期性配送时间和次数分别为T_w和R_w, 则当 $Q_{1}^{w}$ =…= $Q_{r}^{w}$ =…= $\begin{matrix} Q_{R_{w}}^{w} \end{matrix}$ 时, Z₂(T_w)取最小值。

证明若工人w负责工位m, …, n, 则D_w为定值。Z₂(T_w)= $\begin{matrix} \frac{1}{R_{w}} \end{matrix} \begin{matrix} \overset{R_{w}}{\sum_{r = 1}} \end{matrix} \begin{matrix} \frac{D_{w}}{Q_{r}^{w}} \end{matrix}$ = $\begin{matrix} (\frac{D_{w}}{Q_{1}^{w}} \end{matrix}$ +…+ $\begin{matrix} \frac{D_{w}}{Q_{r}^{w}} \end{matrix}$ +…+ $\begin{matrix} \frac{D_{w}}{Q_{R_{w}}^{w}}) / \end{matrix}$ R_w, 故当Δ = $\begin{matrix} \frac{D_{w}}{Q_{1}^{w}} \end{matrix}$ +…+ $\begin{matrix} \frac{D_{w}}{Q_{r}^{w}} \end{matrix}$ +…+ $\begin{matrix} \frac{D_{w}}{Q_{R_{w}}^{w}} \end{matrix}$ 取最小值时, 则Z₂(T_w)取得最小值。根据数学不等式性质可得:

$\begin{matrix} (\frac{1}{Q_{1}^{w}} + \dots + \frac{1}{Q_{r}^{w}} + \dots + \frac{1}{Q_{R_{w}}^{w}}) \end{matrix}$ · (+…++…+ $\begin{matrix} Q_{R_{w}}^{w} \end{matrix}$ )≥

$\begin{matrix} (1 + \frac{Q_{2}^{w}}{Q_{1}^{w}} + \dots + \frac{Q_{r}^{w}}{Q_{1}^{w}} + \dots + \frac{Q_{R_{w}}^{w}}{Q_{1}^{w}}) \end{matrix}$ + $\begin{matrix} (\frac{Q_{1}^{w}}{Q_{2}^{w}} + 1 + \dots + \frac{Q_{R_{w}}^{w}}{Q_{2}^{w}}) \end{matrix}$ +…+

$\begin{matrix} (\frac{Q_{1}^{w}}{Q_{R_{w}}^{w}} \end{matrix}$ +…+ $\begin{matrix} \frac{Q_{r}^{w}}{Q_{R_{w}}^{w}} + \dots + 1) \end{matrix}$

当且仅当1/=…=1/=…=1/ $\begin{matrix} Q_{R_{w}}^{w} \end{matrix}$ , 即=…==…= $\begin{matrix} Q_{R_{w}}^{w} \end{matrix}$ , “ =” 成立, 引理1得证。

定理2 送料工人w负责工位m, …, n, 若存在可行周期性配送时间、, 对应配送次数X、Y, 且a_i、b_j(i=1, 2, …, X; j=1, 2, …, Y)分别表示每次配送的量, 则当> , 即X< Y时, Z₂()< Z₂()。

证明根据引理1可得:

Z₂()= $\begin{matrix} [X \cdot D_{w} / (\overset{X}{\sum_{i = 1}} a_{i} / X)] \end{matrix}$ /X=X· D_w $\begin{matrix} / \overset{X}{\sum_{i = 1}} a_{i} \end{matrix}$ ,

Z₂()= $\begin{matrix} [Y \cdot D_{w} / (\overset{Y}{\sum_{j = 1}} b_{j} / Y)] \end{matrix}$ /Y=Y· D_w $\begin{matrix} / \overset{Y}{\sum_{j = 1}} b_{j} \end{matrix}$ 。

根据约束(7)可得:

$\begin{matrix} \overset{X}{\sum_{i = 1}} \end{matrix}$ a_i= $\begin{matrix} \overset{Y}{\sum_{j = 1}} \end{matrix}$ b_j= $\begin{matrix} \overset{n}{\sum_{s = m}} \end{matrix} \begin{matrix} \overset{T}{\sum_{t = 1}} \end{matrix}$

故Z₂()< Z₂(), 即定理2得证。

定理3 当送料工人数量保持不变时, 存在一个可行的工位分配方案Ω ={1, δ ₂, …, δ _w, …, S+1}。对δ _w进行± 1操作变为δ '_w, 构成邻域解Ω '={1, δ ₂, …, δ '_w, …, S+1}, 对应D'_w← D_w, T'_w← T_w, R'_w← R_w。若Z₂(T'_w)< Z₂(T_w), 则该邻域解优于原方案。

证明定理3显然成立。当Z₂(T'_w)< Z₂(T_w)时, 且工人数保持不变, 即固定成本不变, 则由式(11)可知Z(Ω ')< Z(Ω ), 即该领域解较优。

2.2 嵌套启发式动态规划算法

根据模型P₁, 需决策每个工人w负责的最左边工位, 继而可知其负责的所有工位。故将决策过程划分为+1个阶段, 每阶段表示一个工位, i=1, 2, …, +1, +1为终止阶段。每阶段的状态亦为i, 表示工人负责的最左边工位, 从状态i到状态j, 即表示w负责工位i, …, (j-1), 从1到+1依次进行前向递归, 并计算状态转移对应目标函数值的变化:

μ (i, j)=F_w+u· $\begin{matrix} \overset{R_{w}^{*}}{\sum_{r = 1}} \end{matrix} \begin{matrix} Q_{r}^{w*} \end{matrix}$ · Z₂(T^*_w) (12)

式中:“ * ” 为i, …, (j-1)工位周期性配送问题最优解。

用H(i)表示从工位1到i的最优目标函数值, 则:

H(j)= $\begin{matrix} \min_{1 \leq i \leq j - 1} \end{matrix}$ {H(i)+μ (i, j)}(13)

结合式(12)(13)可得最优解H(+1), 采用反向回溯即可得最优工位分配。但是, 由于两个子问题相互关联, 因此在利用动态规划求解时, 每阶段都需计算D_w、、及相应Z₂(), 即对问题P₂进行求解。设w负责工位i, …, (j-1), 结合引理定理, 周期性配送问题求解步骤如下, 其实质上是对于T_w解空间的全枚举。

Step1 计算工位s(s=i, …, j-1)最少配送次数: $\begin{matrix} {\underline{N}}_{s} \end{matrix}$ =「 $\begin{matrix} \overset{T}{\sum_{t = 1}} \end{matrix}$ /B_s⌉, 取N'=max{ $\begin{matrix} {\underline{N}}_{i} \end{matrix}$ , …, $\begin{matrix} {\underline{N}}_{j - 1} \end{matrix}$ }。

Step2 计算该子区域i, …, (j-1)最少配送次数: $\begin{matrix} {\underline{N}}_{w} \end{matrix}$ =「 $\begin{matrix} \overset{j - 1}{\sum_{s = i}} \end{matrix} \begin{matrix} \overset{T}{\sum_{t = 1}} \end{matrix}$ /C_w⌉。

Step3 根据Step1和Step2确定w最少配送次数 $\begin{matrix} {\underline{N}}_{w}^{\min} \end{matrix}$ =max(N', $\begin{matrix} {\underline{N}}_{w} \end{matrix}$ )。

Step4 计算w配送次数R_w∈ [ $\begin{matrix} {\underline{N}}_{w}^{\min} \end{matrix}$ , T], 相应周期时间T_w∈ $[1, ⌊T / {\bar{N}}_{w}^{\min}⌋]$ 。

Step5 确定T_w和Z₂(), 根据定理2选择T_w, 并验证约束(8)(9)。

上述嵌套算法的复杂度为O(· T²), 随着规模的增大, 其求解时间呈指数倍上升, 无法求解中、大规模问题。

2.3 改进型和声搜索算法

为了有效求解中、大规模问题, 引入和声搜索算法(Harmony search, HS), 该算法原理简单、控制参数少、收敛速度快, 且文献[9]证明了其解决离散问题时的全局收敛性, 已成功应用于各类非线性优化问题^[10]。然而, HS算法仍存在搜索后期收敛较慢、局部探索能力差、易陷入局部最优等缺陷。因此, 提出了一种改进型和声搜索算法MHSA, 基本流程如下。

Step1 参数初始化。给定和声记忆库大小HMS、精度ε 、最大迭代次数SNI及参数HMCR, PAR。

Step2 初始化和声记忆库。结合约束(2)(3)(4), 随机产生HMS个和声, 存入记忆库。

Step3 按照和声长度(即所需工人数)将和声记忆库分解成为若干个子和声记忆库。

Step4 对于每个子和声记忆库, 基于HMCR、PAR进行即兴创作, 产生新的和声向量。

Step5 更新子和声记忆库, 即判断新和声向量是否优于当前子和声记忆库中最差和声。

Step6 判断子和声记忆库终止准则, 若当前迭代次数sk大于最大迭代次数SNI, 则合并所有子和声记忆库构成新的和声记忆库, 否则重复Step4、Step5。

Step7 对记忆库最差和声向量X^w¹、X^w²进行交叉、变异形成新和声X'、X″, 并更新和声记忆库。

Step8 判断终止准则。若任两个和声对应目标值之差均小于精度ε , 终止算法, 否则重复Step3~Step7。

2.3.1 和声编码方式

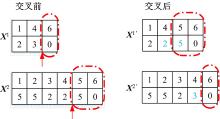
和声向量Xⁱ采用变长双层编码方式^[11], i=1, 2, …, HMS。由编码长度可得所需送料工人数, 即(-1)。第一层为工位层, 代表各工人负责的最左边工位δ _w。根据约束(2)(3)(4)可知其以1开始, 以+1结束, 且升序排列。第二层为时间层, 代表工人配送时间间隔T_w。图2所示为以上算例的两个和声编码示意图。其中, X¹即为最优解, 可行解X²表示由5个工人分别负责1个工位, 且其对应配送时间间隔分别为5、5、2、2、5个周期。

	Figure Option View Download New Window
	图2 和声编码示意图Fig.2 Diagram of encoded mode for harmony vector

2.3.2 初始化和声记忆库

给定S, 则和声的最大长度Len_max=+1; 根据定理1计算最少送料工人数, 则Len_min= $\begin{matrix} {|W|}_{\min} \end{matrix}$ +1。因此, 和声Xⁱ(i=1, 2, …, HMS)的长度范围为[Len_min, Len_max]。分别用¹, ²X表示和声Xⁱ第一、二层编码的第j列, Len_i=。为生成初始可行解, 结合约束(2)(3)(4)随机生成HMS个和声, ∀ i=1, 2, …, HMS, 和声Xⁱ满足:

$\begin{matrix} \{\begin{matrix} ^{1} X_{1}^{i} = 1,^{1} X_{j}^{i} <^{1} X_{j + 1}^{i},^{1} X_{Le n_{i}}^{i} = |S| + 1 \\ ^{2} X_{1}^{i} = \dots =^{2} X_{j}^{i} = \dots =^{2} X_{Le n_{i} - 1}^{i} = 1,^{2} X_{Le n_{i}}^{i} = 0 \end{matrix} \end{matrix}$ (14)

根据和声Xⁱ计算对应函数值f(Xⁱ), 一并存入和声记忆库HM, 即实现和声记忆库的初始化。

2.3.3 子和声记忆库操作

Chen等^[12]指出, 对于中等规模的问题, 通常采用较小的HM优于较大的HM, 即应该设置较小的HMS。因此, 本文将HM按照和声长度Len_i划分成大小不同的若干子和声记忆库Sub-HM。对于每个Sub-HM, 为防止算法过早收敛、陷入局部最优, 结合参数HMCR、PAR等创作新和声, 并不断更新Sub-HM。

对于每个Sub-HM, 新和声X^new以HMCR概率继承现有Sub-HM中和声, 并以PAR概率进行微调。由于编码的特殊性, 结合定理3, 对X^new进行邻域搜索。新和声X^new以(1-HMCR)的概率进行创作, 不同于HS中按定义域随机生成 $\begin{matrix} X_{j}^{new} \end{matrix}$ , 本文采用轮盘赌算法从Sub-HM中选取两个和声X^a、X^b, 并引入比例系数α 生成新和声元素¹ $\begin{matrix} X_{j}^{new} \end{matrix}$ 。为进一步加快算法收敛速度, 求得较优解, 沿用2.2中的启发式算法求² $\begin{matrix} X_{j}^{new} \end{matrix}$ 。最后, 计算新和声X^new和最差和声X^worst对应目标函数值f(X^new)和f(X^worst), 并比较、更新Sub-HM。

2.3.4 更新和声记忆库

为进一步增加和声多样性并改善解质量, 对于重组后HM中的和声进行交叉、变异操作, 具体流程如下。

(1)交叉操作

给定交叉概率P_c, 根据

X^w← argmax{f(Xⁱ)}, i=1, 2, …, HMS

选取两个和声 $\begin{matrix} X^{w_{1}} \end{matrix}$ , $\begin{matrix} X^{w_{2}} \end{matrix}$ , 若rand(0, 1)< P_c, 则:

Step1 随机选取 $\begin{matrix} X^{w_{1}} \end{matrix}$ 、 $\begin{matrix} X^{w_{2}} \end{matrix}$ 的交叉点C₁、C₂, 记L₁= $\begin{matrix} |X^{w_{1}}| \end{matrix}$ , L₂= $\begin{matrix} |X^{w_{2}}| \end{matrix}$ , 则新和声X'、X″长度分别为L'=C₁+L₂-C₂, L″=C₂+L₁-C₁。

Step2 若¹ $\begin{matrix} X_{C_{1} + 1}^{w_{1}} \end{matrix}$ > ¹ $\begin{matrix} X_{C_{2}}^{w_{2}} \end{matrix}$ & ¹ $\begin{matrix} X_{C_{2} + 1}^{w_{2}} \end{matrix}$ > ¹ $\begin{matrix} X_{C_{1}}^{w_{1}} \end{matrix}$ & L'≤ +1 & L″≤ +1, 转Step3, 否则转Step4。

Step3对 $\begin{matrix} X^{w_{1}} \end{matrix}$ 、 $\begin{matrix} X^{w_{2}} \end{matrix}$ 在C₁、C₂处交叉, 结合2.2节中Step1~ Step 5求相应²X'_j、²X″_j, 形成新和声X'、X″, 并求f(X'), f(X″)。

Step4 重新生成交叉点C₂, 并转Step3。

Step5 和声 $\begin{matrix} X^{w_{1}} \end{matrix}$ 、 $\begin{matrix} X^{w_{2}} \end{matrix}$ 交叉结束。

如图3所示, 分别选取X¹、X²(L₁=3, L₂=6)的交叉点C₁=2, C₂=4, 按照Step2和Step3进行交叉, 并重新计算周期性配送时间, 得到两个长度分别为L'₁=4, L'₂=5的新和声X¹^'、X²^'。

	Figure Option View Download New Window
	图3 交叉操作示意图Fig.3 Diagram of crossover operation

(2)变异操作

和声 $\begin{matrix} X^{w_{1}} \end{matrix}$ 、 $\begin{matrix} X^{w_{2}} \end{matrix}$ 经交叉后变为X'、X″, 若f(X')< f( $\begin{matrix} X^{w_{1}} \end{matrix}$ )f(X″)< f( $\begin{matrix} X^{w_{2}} \end{matrix}$ ), 则 $\begin{matrix} X^{w_{1}} \end{matrix}$ ← X', $\begin{matrix} X^{w_{2}} \end{matrix}$ ← X″; 否则记X^chng为待变异和声, 引入变异概率P_m, 若rand(0, 1)< P_m, 进行如下操作:

Step1 随机选取一列:j=rand(1, $\begin{matrix} |X^{chng}| \end{matrix}$ )。

Step2 结合约束(3)进行随机变异:¹ $\begin{matrix} X_{j}^{chng} \end{matrix}$ =rand(¹ $\begin{matrix} X_{j - 1}^{chng} \end{matrix}$ , ¹ $\begin{matrix} X_{j + 1}^{chng} \end{matrix}$ ), 并根据2.3.3节中Step1~Step5求相应² $\begin{matrix} X_{j}^{chng} \end{matrix}$ , 形成邻域解X^chng。

Step3 计算f(X^chng), 若f(X^chng)< f( $\begin{matrix} X^{w_{1}} \end{matrix}$ ), 则 $\begin{matrix} X^{w_{1}} \end{matrix}$ ← X^chng, 否则转Step1。

Step4 和声X^chng变异结束。

3 仿真实验与分析

为评价该线边集成超市物料配送系统及MHSA算法, 结合文献[5]生成如下实验参数。该混流装配线生产多种车型, 工位s(s∈ S)在周期t=1, 2, …, T所需物料=⌊rnd^uni(0, 3)⌉, 即采用(0, 3)的均匀分布, ⌊· ⌉表示就近取整, 同理:B_s=⌊rnd^uni(5, 10)⌉, C_w=⌊rnd^uni(5, 8)⌉。系统节拍时间ct=100 s, 且st=0.1ct, wt=0.2ct, at_w=0.3ct。分别取不同的和T组合, 每种组合运行20次并进行统计分析。

3.1 有效性验证

为验证MHSA的有效性, 将其与嵌套启发式动态规划算法进行比较, 其计算机运行时限设置为1800 s, 若求解超过时限, 即视为中大规模问题, 无法求得最优解。表1为小规模问题参数和实验结果。其中, MHSA方法的相关参数如HMCR、PAR参见文献[9]推荐值, 初始和声记忆库大小为HMS=2· |S|。动态规划方法求得最优解, MHSA运行20次后取平均值, 由表1可知, 其与最优解的偏差Gap均小于5%, 即可得到满意解, 验证了该算法的有效性。同时, 随着问题规模扩大, 偏差减小, 表明随着问题规模扩大, MHSA的记忆库扩大, 和声多样性增加, 避免局部最优, 因此, MHSA适用于求解中大规模的问题。

表1 小规模问题的实验参数和结果 Table 1 Parameters and results of small scale problems

3.2 算法比较

3.2.1 比较MHSA、ACO和SA

MHSA模拟音乐家创作优美和声的过程, 将其与其他模拟自然现象的优化算法进行比较, 包括蚁群算法(Ant colony optimization, ACO)和模拟退火算法(Simulated annealing, SA)。问题规模和结果如表2所示。

表2 MHSA、ACO和SA的结果比较 Table 2 Experimental results of MHSA, ACO & SA

由表2可知, 随着问题规模T和的扩大, MHSA算法的寻优能力优于ACO和SA等优化算法。尤其在较大规模情况下(T≥ 100, ≥ 50), ACO和SA与MHSA的目标函数值Gap均超过5%, MHSA算法深度的搜索能力更为突出, 一定程度上验证了MHSA算法处理中大规模问题时的有效性。

图4(a)(b)分别为MHSA、ACO和SA算法在T=20, =10和T=100, =50时的收敛曲线。由图4(a)可知, 在问题规模较小时, MHSA、ACO均能快速收敛; 而随着问题规模的扩大, 本文提出的子和声记忆库操作加快算法的收敛速度, 结合交叉变异等操作扩大邻域搜索范围, 避免陷入局部最优, 使MHSA明显优于ACO和SA算法, 如图4(b)所示。

	Figure Option View Download New Window
	图4 算法收敛性能比较Fig.4 Convergence performance of algorithms

3.2.2 比较MHSA、IHS、GHS和NGHS

为进一步说明MHSA算法可有效避免或减少HS算法早熟收敛、易陷入局部最优的缺点, 如图5所示, 将其与目前引用较广泛的IHS^[13]、GHS^[14]和NGHS^[15]进行对比。

图5(a)为=40, 取不同T时各个算法的比较结果。由图可知, MHSA算法在不同规模下的目标函数值明显优于其他算法, 它们与MHSA算法的偏差基本分布在区间[5%, 20%]。同理, 图5(b)为T=120, 取不同工位数时的对比情况, 其优化结果的偏差主要分布在区间[10%, 30%]。且MHSA的结果与呈近似线性关系, 一定程度上体现了算法的有效性。因此, 本文提出的局部交叉变异等操作在一定程度上提升了MHSA算法的搜索深度, 避免陷入局部最优, 使MHSA优于IHS、GHS和NGHS等算法。

	Figure Option View Download New Window
	图5 MHSA、IHS、GHS和NGHS结果比较Fig.5 Experimental results of MHSA, IHS, GHS and NGHS

3.2.3 参数分析

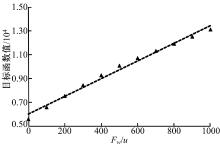
为最小化线边超市供料系统的运行成本, 必须找到一个平衡点, 使送料工人的雇佣成本与物料配送成本之和最小, 根据式(11)可知, 其受参数F_w和u影响。令问题规模T=20, =10, 参数u=1保持不变, F_w分别取0, 100, 200, …, 1000, 则F_w/u对目标函数值的影响如图6所示。由图可知, 随着F_w/u线性递增, 对应目标函数值也基本呈线性递增, 斜率约为7.54, 即所需的平均送料工人数; 截距约为6028.54, 即物料配送成本。

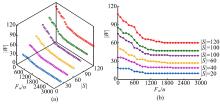
	Figure Option View Download New Window
	图6 F_w/u对目标函数值的影响Fig.6 Effect of F_w/u on objectives

根据以上分析可知, F_w/u的变化主要影响送料工人数量。取F_w/u∈ [0, 3000], 令T=20, 分别取为20, 40, …, 120, 则相应的工人数随F_w/u变化的情况如图7所示, 其中, 图7(b)为图7(a)在YOZ平面投影。由图7可知, 当生产周期数T一定时, 随着增加, 所需工人数增加。对任意给定, 随F_w/u的增加而减少, 且减少到一定程度(约|S|/2, 即平均1个工人负责2个工位)后保持不变, 即得到该T、|S|情形下满足所有约束条件的最小工人数, 此时增加F_w/u仅对目标函数有影响, 对无影响。

	Figure Option View Download New Window
	图7 F_w/u对送料工人数量的影响Fig.7 Effect of F_w/u on number of logistics operators

4 结束语

本文将新型线边集成超市物料配送分解为工位分配和周期性配送调度问题进行研究, 并以最小化送料工人固定成本和物料的配送成本为目标建立数学模型进行求解。针对该关联问题, 提出相应的引理、定理, 并建立嵌套启发式动态规划方法以获取小规模问题的精确解; 对于中大规模问题, 构建了改进型和声搜索算法(MHSA)获取满意解。最后, 通过仿真实验与其他模拟算法或改进算法进行对比, 验证了MHSA的可行性和有效性。后续为提升工人的利用率, 将对一组送料工人共同负责一个装配区域的情况进行研究。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Lau H Y K, Woo S O. An agent-based dynamic routing strategy for automated material hand ling systems[J]. International Journal of Computer Integrated Manufacturing, 2008, 21(3): 269-288. [本文引用:1]
[2]	Sali M, Sahin E, Patchong A. An empirical assessment of the performances of three line feeding modes used in the automotive sector: line stocking vs. kitting vs. sequencing[J]. International Journal of Production Research, 2015, 53(5): 1439-1459. [本文引用:1]
[3]	Caputo A C, Pelagagge P M, Salini P. A decision model for selecting parts feeding policies in assembly lines[J]. Industrial Management & Data Systems, 2015, 115(6): 974-1003. [本文引用:1]
[4]	Battini D, Boysen N, Emde S. Just-in-time supermarkets for part supply in the automobile industry[J]. Journal of Management Control, 2013, 24(2): 209-217. [本文引用:1]
[5]	Boysen N, Emde S, Hoeck M, et al. Part logistics in the automotive industry: decision problems, literature review and research agenda[J]. European Journal of Operational Research, 2015, 242(1): 107-120. [本文引用:1]
[6]	周炳海, 徐佳惠. 基于支持向量机的多载量小车实时调度[J]. 吉林大学学报: 工学版, 2016, 46(6): 2027-2033. Zhou Bing-hai, Xu Jia-hui. SVM-based real-time scheduling approach of multi-load carriers[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(6): 2027-2033. [本文引用:1]
[7]	Boysen N, Emde S. Scheduling the part supply of mixed-model assembly lines in line-integrated supermarkets[J]. European Journal of Operational Research, 2014, 239(3): 820-829. [本文引用:1]
[8]	Battini D, Gamberi M, Persona A, et al. Part-feeding with supermarket in assembly systems: transportation mode selection model and multi-scenario analysis[J]. Assembly Automation, 2015, 35(1): 149-159. [本文引用:1]
[9]	赵玉新, Yang X S, 刘利强. 新兴元启发式优化方法[M]. 北京: 科学出版社, 2013: 201, 202, 216-218. [本文引用:1]
[10]	Manjarres D, Land a-Torres I, Gil-Lopez S, et al. A survey on applications of the harmony search algorithm[J]. Engineering Applications of Artificial Intelligence, 2013, 26(8): 1818-1831. [本文引用:1]
[11]	Zhou B, Peng T. Scheduling the in-house logistics distribution for automotive assembly lines with just-in-time principles[J]. Assembly Automation, 2017, 37(1): 51-63. [本文引用:1]
[12]	Chen J, Pan Q K, Wang L, et al. A hybrid dynamic harmony search algorithm for identical parallel machines scheduling[J]. Engineering Optimization, 2012, 44(2): 209-224. [本文引用:1]
[13]	Mahdavi M, Fesanghary M, Damangir E. An improved harmony search algorithm for solving optimization problems[J]. Applied Mathematics and Computation, 2007, 188(2): 1567-1579. [本文引用:1]
[14]	Omran M G H, Mahdavi M. Global-best harmony search[J]. Applied Mathematics and Computation, 2008, 198(2): 643-656. [本文引用:1]
[15]	Zou D, Gao L, Li S, et al. Solving 0-1 knapsack problem by a novel global harmony search algorithm[J]. Applied Soft Computing, 2011, 11(2): 1556-1564. [本文引用:1]

2008

0.0

... 0 引言物料配送(Part feeding)占车辆生产成本的20%~50%^[1] ...

2015

0.0

... 许多国内外学者对传统送料机制,即线边储料(Line stocking)和成套供料(Kitting)进行了广泛的对比和研究^[2,3],并指出不存在绝对的最优机制,应根据物料特性和实际生产环境选用不同送料机制才可有效降低系统配送总成本 ...

2015

0.0

2013

0.0

... 近年来,研究焦点逐渐转移为准时化配送策略^[4,5],即采用物料超市(Supermarket)替代传统的中心仓库存放物料,通过对多载量小车等送料设备的调度^[6]实现物料的小批量多频次配送 ...

2015

0.0

2016

0.0

. 2016, 46(6):2027-2033 DOI:doi:10.13229/j.cnki.jdxbgxb201606036

SVM-based real-time scheduling approach of multi-load carriers

基于支持向量机的多载量小车实时调度

Zhou Bing-hai , Xu Jia-hui.

周炳海, 徐佳惠

摘　要：为了有效地解决车辆装配系统中多载量小车的实时调度问题,提出了基于支持向量机的实时调度方法。首先对多载量小车的实时调度问题进行描述,同时建立以车辆装配线产量和物料搬运距离作为评价指标的目标函数。然后通过车辆装配线的物料搬运系统仿真生成样本离线训练支持向量机模型,在实时阶段利用支持向量机模型实现多载量小车＂等待＂或＂搬运＂的调度决策。试验结果表明,本文提出的方法明显优于最小批量法,其运行速度快、实时调度效果好,且对动态环境变化具有一定的自适应性,能够有效提升多载量小车的实时调度水平。

2014

0.0

... 为充分结合传统线边储料、成套供料以及准时化配送策略的优势,降低系统总运作成本,Boysen等^[7]结合某德国汽车制造商的实际运营情况,提出并介绍了#cod#x0201c ...

2015

0.0

... Battini等^[8]对厂内物流进行研究时也简单提及了#cod#x0201c ...

2013

0.0

2013

0.0

... 3 改进型和声搜索算法为了有效求解中、大规模问题,引入和声搜索算法(Harmony search, HS),该算法原理简单、控制参数少、收敛速度快,且文献[9]证明了其解决离散问题时的全局收敛性,已成功应用于各类非线性优化问题^[10] ...

2017

0.0

... 和声向量Xⁱ采用变长双层编码方式^[11],i=1,2,…,HMS ...

2012

0.0

... Chen等^[12]指出,对于中等规模的问题,通常采用较小的HM优于较大的HM,即应该设置较小的HMS ...

2007

0.0

... 为进一步说明MHSA算法可有效避免或减少HS算法早熟收敛、易陷入局部最优的缺点,如图5所示,将其与目前引用较广泛的IHS^[13]、GHS^[14]和NGHS^[15]进行对比 ...

2008

0.0

2011

0.0