双门限唐检测改进算法

引用本文

张超逸, 李金海, 阎跃鹏. 双门限唐检测改进算法. 2018, 48(2): 610-617
ZHANG Chao-yi, LI Jin-hai, YAN Yue-peng. Improved Tong detection algorithm with double thresholds. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 610-617 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161369
Permissions

双门限唐检测改进算法

张超逸^1,², 李金海¹, 阎跃鹏¹

1.中国科学院微电子研究所,北京 100029

2.中国科学院大学,北京 100049

作者简介:张超逸(1990-),男,博士研究生. 研究方向:卫星导航技术. E-mail:zhangchaoyi@ime.ac.cn

基金项目:国家自然科学基金项目(61271423)

摘要

针对传统唐检测算法中驻留次数过多导致检测确认速度较慢的问题,提出了一种基于双门限的唐检测改进算法。该算法将检测统计量与两级门限相比较,并根据比较结果对检测计数器进行加减操作,使计数器值能更快速地满足检测条件,从而减少了检测时间。对双门限唐检测改进算法的系统虚警概率、系统检测概率和平均驻留次数进行了理论推导与仿真验证。仿真结果表明,通过合理设置第二级门限的数值,改进算法可在检测性能基本不受影响的前提下有效减少平均驻留次数,提高检测确认速度。

关键词: 通信技术; 全球导航卫星系统; 唐检测; 双门限; 平均驻留次数

中图分类号:TN911.23 文献标志码:A 文章编号:1671-5497(2018)02-0610-08

Improved Tong detection algorithm with double thresholds

ZHANG Chao-yi^1,², LI Jin-hai¹, YAN Yue-peng¹

1.Institute of Microelectronics of Chinese Academy of Sciences, Beijing 100029, China

2.University of Chinese Academy, Beijing 100049, China

Abstract

Long due time in traditional Tong detection algorithm results in slow speed of detection and confirmation. In order to solve this problem, an improved Tong detection algorithm with double thresholds is proposed. By comparing the detection statistic with two-stage thresholds, the detection condition of the algorithm can be met more quickly after a few logical operations on the counter, which greatly reduces the detection time. The false alarm probability, the detection probability and the average dwell times of the proposed algorithm are analyzed and verified. Simulation results indicate that the proposed algorithm can maintain the detection performance and reduce the average dwell rimes effectively if a second threshold is set suitably.

Key words: communication technology; global navigation satellite system; Tong detection; double thresholds; average dwell times

Show Figures

0 引言

全球导航卫星系统(Global navigation satellite system, GNSS)采用直接序列扩频技术实现定位、测速和授时功能。在导航接收机设计中, 需要完成信号在时域和频域的二维捕获, 并对每个捕获单元的结果进行检测确认^{[1, 2, 3]}。最基本的检测确认方法是对每个单元的信号进行积分和清零, 将得到的包络与门限相比较, 以确定卫星信号是否存在。由于单次驻留检测的虚警概率过高, 无法满足系统要求, 需采用多次驻留检测来对捕获结果进行确认^[4]。唐检测算法凭借可变的驻留次数、计算量少、结构简单以及在低信噪比下良好的检测性能得到了广泛的应用^[5]。为了提升检测性能, 文献[6]提出了含近邻约束的改进唐检测算法, 增强对弱信号的检测能力, 但检测速度并未得到有效提高。为解决驻留次数不确定导致检测器长时间驻留在某个捕获单元中的问题, 文献[7]提出了对单次检测的总次数设置门限进行约束的方法, 通过选择合理的次数门限, 使得在检测性能不受影响的条件下可以有效控制检测次数, 但该算法主要针对弱信号情况, 对平均驻留次数影响有限。文献[8]在捕获模块之前增加了一个能量估计模块, 通过自适应调整门限和驻留次数来提高检测性能, 但检测速度受能量估计值影响较大, 同时会带来大量额外的计算复杂度。检测速度对接收机至关重要, 直接决定了卫星从捕获状态转至跟踪状态所需的时间。为了加快检测速度, 本文基于传统唐检测算法, 提出了采用双门限比较的唐检测改进算法, 该算法将信号包络与两级门限分别比较后作出检测判决, 在检测性能基本不受影响的前提下, 有效降低了平均驻留次数, 减少了检测确认时间。

1 检测统计量

接收机天线接收到导航信号后通过射频模块下变频为数字中频信号, 再经过解调、解扩、相干积分和清零之后得到I、Q两路信号的表达式如下^[9]:

$\begin{matrix} \{\begin{matrix} I (n) = aD (n) R (τ) sinc (f_{e} T) \cos (φ_{e}) + n_{I} \\ Q (n) = aD (n) R (τ) sinc (f_{e} T) \sin (φ_{e}) + n_{Q} \end{matrix} \end{matrix}$ (1)

式中:a为信号幅值; D为相干积分时间内调制的导航电文; R为扩频码自相关函数; τ 为本地码与输入信号之间的码相位差; T为相干积分时长; f_e为本地载波和输入信号的载波频率差; φ _e为本地载波和输入信号的载波相位差; n_I和n_Q为互不相关的均值为零、方差为的高斯白噪声。

对I、Q两路信号进行如下式的非相干积分:

V²= $\begin{matrix} \overset{N_{nc}}{\sum_{n = 1}} \end{matrix}$ [I²(n)+Q²(n)](2)

本文取V²作为单次检测的检测统计量, 即对N_nc个I、Q两路信号的相干积分功率和进行累加。当卫星信号不存在时, V²服从自由度为2N_nc的中心卡方(χ ²)分布。令y=v², 则其概率密度函数为^[10]:

p_n(y)= $\begin{matrix} \frac{1}{σ^{2 N_{nc}} 2^{N_{nc}} Γ (N_{nc})} \end{matrix} \begin{matrix} y^{N_{nc} - 1} \end{matrix} \begin{matrix} e^{- y / 2 σ_{n}^{2}} \end{matrix}$ (3)

式中:Γ (p)为γ 函数。此时的概率密度函数仅与相干积分后的噪声功率、非相干次数有关。当卫星信号存在时, V²服从自由度为2N_nc的非中心卡方分布。

令y=v², 则其概率密度函数为^[10]:

p_s(y)= $\begin{matrix} \frac{1}{2 σ_{n}^{2}} \end{matrix} \begin{matrix} {(\frac{y}{s^{2}})}^{(N_{nc} - 1) / 2} \end{matrix} \begin{matrix} e^{- (s^{2} + y \frac{)}{2} σ_{n}^{2}} \end{matrix} \begin{matrix} I_{N_{nc} - 1} \end{matrix} \begin{matrix} (\sqrt[]{y} \frac{s}{σ_{n}^{2}}) \end{matrix}$ (4)

式中:I_α(x)为第一类α 阶修正贝塞尔函数; s²称为非中心分布参量, 考虑码相位偏差τ 与载波频率偏差f_e均为0的情况下定义为:

s²=a²N_nc(5)

可以看出此时的概率密度函数还与输入信号的功率有关。

单次检测的虚警概率计算表达式如下:

P_fa= $\begin{matrix} \int_{V_{t}}^{\infty} \end{matrix}$ p_n(y)dy= $\begin{matrix} e^{- V_{t} / 2 σ_{n}^{2}} \end{matrix} \begin{matrix} \overset{N_{nc} - 1}{\sum_{k = 0}} \end{matrix} \begin{matrix} {(\frac{V_{t}}{2 σ_{n}^{2}})}^{k} \end{matrix}$ (6)

式中:V_t为检测门限值。

单次检测的检测概率计算表达式如下:

P_d= $\begin{matrix} \int_{V_{t}}^{\infty} \end{matrix}$ p_s(y)dy= $\begin{matrix} Q_{N_{nc}} \end{matrix}$ ( $\begin{matrix} \frac{s}{σ_{n}} \end{matrix}$ , $\begin{matrix} \frac{\sqrt[]{V_{t}}}{σ_{n}} \end{matrix}$ )(7)

式中:Q_m(a, b)为广义马库姆(Marcum's)Q函数。

由式(6)(7)可知, 在相同检测条件下, 虚警概率越低, 所需的检测门限值越大, 相应的检测概率也越低, 因此, 在虚警概率和检测概率之间需要取得折中。检测时采用Neyman-Pearson准则, 在给定单次检测的虚警概率P_fa和由接收机估计得到的噪声功率后由式(6)计算得到检测门限V_t, 然后再由式(7)计算得到单次检测的检测概率P_d。

2 唐检测算法介绍

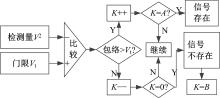
唐检测算法是一种可变驻留次数的检测确认算法, 其将检测统计量与门限相比较, 若大于门限, 则检测计数器K加1; 若小于门限, 则检测计数器K减1。经过多次检测后, 当K达到次数门限A时, 认为信号存在。当K=0时, 认为信号不存在。这里K的初始值取B。算法流程图如图1所示。

	Figure Option View Download New Window
	图1 唐检测器检测算法流程Fig.1 Flow diagram of Tong detection algorithm

文献[11]给出了唐检测算法的系统虚警概率为:

P_FA= $\begin{matrix} \frac{[(1 - P_{fa}) / P_{fa}]^{B} - 1}{[(1 - P_{fa}) / P_{fa}]^{A} - 1} \end{matrix}$ (8)

系统检测概率为:

P_D= $\begin{matrix} \frac{[(1 - P_{d}) / P_{d}]^{B} - 1}{[(1 - P_{d}) / P_{d}]^{A} - 1} \end{matrix}$ (9)

捕获单元仅包含噪声时(噪声单元)的平均驻留次数为^[12]:

N_n= $\begin{matrix} \frac{B}{1 - 2 P_{fa}} \end{matrix}$ - $\begin{matrix} \frac{A}{1 - 2 P_{fa}} \end{matrix}$ × $\begin{matrix} \frac{[(1 - P_{fa}) / P_{fa}]^{B} - 1}{[(1 - P_{fa}) / P_{fa}]^{A} - 1} \end{matrix}$ (10)

捕获单元包含信号时(信号单元)的平均驻留次数为^[13]:

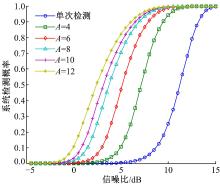
N_s= $\begin{matrix} \frac{B}{1 - 2 P_{d}} \end{matrix}$ - $\begin{matrix} \frac{A}{1 - 2 P_{d}} \end{matrix}$ × $\begin{matrix} \frac{[(1 - P_{d}) / P_{d}]^{B} - 1}{[(1 - P_{d}) / P_{d}]^{A} - 1} \end{matrix}$ (11)

相干积分时长T=1 ms, 非相干次数N_nc=1, 系统虚警概率P_FA=10^-⁶, B=1时, A取不同值、不同信噪比下的系统检测概率P_D如图2所示。

	Figure Option View Download New Window
	图2 唐检测系统检测概率Fig.2 System detection probability of Tong detection

为了进行性能比较, 图2中同时给出了单次检测的检测概率。可以看出, 单次检测要满足检测概率大于90%的条件, 信噪比需要大于13.5 dB, 这样的检测性能是导航接收机无法接受的。而在相同的虚警概率下, 经过唐检测处理后接收机的检测性能得到大幅提升。如当A等于4时, 满足检测概率大于90%所需信噪比仅为9.5 dB, 比单次检测降低4 dB, 且A越大检测性能越好。

表1给出了A取值不同时噪声单元的平均驻留次数, 以及当系统检测概率等于90%时信号单元的平均驻留次数。当仅采用单次检测确认算法时, 在每个捕获单元仅驻留1次。采用唐检测算法后, 由表1可以看出, 信号单元和噪声单元的平均驻留次数都增加, 且信号单元的平均驻留次数远大于噪声单元。随着A的增大, 平均驻留次数也在增加。较大的平均驻留次数会导致接收机检测确认速度过慢, 增加捕获转跟踪所需的时间。因此, 有必要对唐检测算法进行改进, 减少平均驻留次数, 尤其是信号单元的平均驻留次数。

表1 唐检测平均驻留次数 Table 1 Average dwell times of Tong detection

3 本文算法

3.1 算法简介

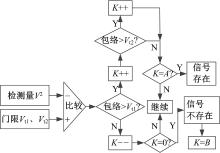
为了有效减少平均驻留次数, 在单门限检测的基础上额外增加另一个较大的门限, 构成两级门限检测。首先, 判断检测统计量与较小的第一级门限的比较结果, 当大于第一级门限时, 检测计数器K加1, 否则, 检测计数器K减1。接着, 判断检测统计量与较大的第二级门限的比较结果, 当大于第二级门限时检测计数器K加1, 否则不做处理。改进算法流程如图3所示。

	Figure Option View Download New Window
	图3 双门限唐检测器检测算法流程Fig.3 Flow diagram of Tong detection algorithm with double thresholds

由于第二级门限较大, 具有较小的虚警概率, 检测通过门限的信号存在概率较大, 这时对检测计数器K再加1是合理的。通过设置两级门限, 在信号存在时, 使得检测计数器K能够更为迅速地接近检测次数门限A, 减少平均驻留次数, 提高检测速度。

3.2 理论分析

唐检测的数学模型可以采用具有两个吸收态的马尔可夫链来描述^{[6, 7]}。每个马尔可夫链包含有一个状态集S和一个转移概率矩阵P。状态集S包含了所有可能出现的状态。从状态i转移到状态j的概率称为转移概率P_ij, 其中i, j∈ S。所有的P_ij组成转移概率矩阵P。当P_ii=1, P_ij=0, i≠ j时, 称状态i为吸收态。唐检测算法对应的状态集S={0, 1, …, A}, 吸收态为0和A。

令第一级门限对应的虚警概率为P_fa1, 第二级门限对应的虚警概率为P_fa2。定义p₀=1-P_fa1表示小于第一级门限的概率; p₁=P_fa1-P_fa2表示大于第一级门限小于第二级门限的概率; p₂=P_fa2表示大于第二级门限的概率。p₀、p₁、p₂均大于0, 且p₀+p₁+p₂=1。由改进算法流程可知, 从状态i到状态i-1的概率为p₀, 从状态i到状态i+1的概率为p₁, 从状态i到状态i+2的概率为p₂, 到其余状态的概率均为0, 则可以得到改进算法的转移概率矩阵如下:

P= $\begin{matrix} [\begin{matrix} 1 & 0 & 0 & 0 & 0 & \dots & 0 \\ p_{0} & 0 & p_{1} & p_{2} & 0 & \dots & 0 \\ 0 & p_{0} & 0 & p_{1} & p_{2} & \dots & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 & 0 & 0 & \dots & p_{2} \\ 0 & 0 & 0 & 0 & 0 & \dots & p_{1} + p_{2} \\ 0 & 0 & 0 & 0 & 0 & \dots & 1 \end{matrix}] \end{matrix}$ (12)

定义从状态i到吸收态A的概率为a_i(i=0, 1, …, A), 则a_i满足如下线性方程组:

$\begin{matrix} \{\begin{matrix} a_{0} = 0 \\ a_{i} = \overset{A}{\sum_{j = 0}} p_{ij} a_{j} \\ a_{A} = 1 \end{matrix} \end{matrix}$ (13)

i=1, 2, …, A-1

将式(12)代入式(13)可得:

$\begin{matrix} \{\begin{matrix} a_{0} = 0 \\ a_{i} = p_{0} a_{i - 1} + p_{1} a_{i + 1} + p_{2} a_{i + 2} \\ a_{A - 1} = p_{0} a_{A - 2} + (p_{1} + p_{2}) a_{A} \\ a_{A} = 1 \end{matrix} \end{matrix}$ (14)

i=1, 2, …, A-2

对式(14)中的a_i表达式进行等价变换可得:

p₀(a_i-a_i-₁)=p₁(a_i+₁-a_i)+p₂(a_i+₂-a_i+₁+a_i+₁-a_i) (15)

令δ _i=a_i+₁-a_i, 则有:

δ _i=pδ _i-₁+qδ _i-₂, i=2, 3, …, A-1 (16)

式中:p=(p₀-1)/p₂; q=p₀/p₂。

式(16)是广义Fibonacci序列, 其通项公式为:

δ _i=λ ₁[(δ ₁-λ ₂δ ₀)-(δ ₁-λ ₃δ ₀)] (17)

式中:λ ₁= $\begin{matrix} \frac{1}{\sqrt[]{p^{2} + 4 q}} \end{matrix}$ , λ ₂= $\begin{matrix} \frac{p - \sqrt[]{p^{2} + 4 q}}{2} \end{matrix}$ , λ ₃= $\begin{matrix} \frac{p + \sqrt[]{p^{2} + 4 q}}{2} \end{matrix}$ 。

对δ _i求和有:

$\begin{matrix} \overset{A - 1}{\sum_{i = 0}} \end{matrix}$ δ _i=a_A-a₀=1(18)

由式(14)中a_A-₁的表达式又有:

δ _A-₁= $\begin{matrix} \frac{p_{0}}{1 - p_{0}} \end{matrix}$ δ _A-₂(19)

联立式(17)(18)(19)可求得δ ₀的表达式。又δ ₀=a₁-a₀=a₁, a₁表示从状态i=B=1出发, 到达吸收态A的概率, 即给定两级门限的虚警概率后可计算得到系统虚警概率为:

P_FA= $\begin{matrix} \frac{1}{λ_{1}} \end{matrix} \begin{matrix} [λ_{3} λ_{5} - λ_{2} λ_{4} + (λ_{4} - λ_{5}) \times \frac{}{} \end{matrix} \begin{matrix} \frac{λ_{2}^{A - 2} λ_{3} λ_{6} - λ_{2} λ_{3}^{A - 2} λ_{6} + λ_{2} λ_{3}^{A - 1} - λ_{2}^{A - 1} λ_{3}}{λ_{3}^{A - 1} - λ_{2}^{A - 1} - λ_{3}^{A - 2} λ_{6} + λ_{2}^{A - 2} λ_{6}}] \end{matrix}$ (20)

式中:λ ₄= $\begin{matrix} \frac{1 - λ_{3}^{A}}{1 - λ_{3}} \end{matrix}$ , λ ₅= $\begin{matrix} \frac{1 - λ_{2}^{A}}{1 - λ_{2}} \end{matrix}$ , λ ₆=- $\frac{q}{p}$ 。

同理, 用两级门限的检测概率P_d1、P_d2代替虚警概率P_fa1、P_fa2, 按照上述推导, 即可得到系统检测概率, 与式(20)形式一致。

定义从状态i到吸收态A或0的平均次数为平均驻留次数μ _i(i=0, 1, …, A), 则μ _i满足如下线性方程组:

$\begin{matrix} \{\begin{matrix} μ_{0} = 0 \\ μ_{i} = \overset{A}{\sum_{j = 0}} p_{ij} μ_{j} + 1 \\ μ_{A} = 0 \end{matrix} \end{matrix}$ (21)

i=1, 2, …, A-1

将式(12)代入式(21), 可得如下方程组:

$\begin{matrix} \{\begin{matrix} μ_{0} = 0 \\ μ_{i} = p_{0} μ_{i - 1} + p_{1} μ_{i + 1} + p_{2} μ_{i + 2} + 1 \\ μ_{A - 1} = p_{0} μ_{A - 2} + (p_{1} + p_{2}) μ_{A} + 1 \\ μ_{A} = 0 \end{matrix} \end{matrix}$ (22)

i=1, 2, …, A-2

令η _i=μ _i+₁-μ _i, 则有:

η _i=pη _i-₁+qη _i-₂+r, i=2, 3, …, A-1(23)

式中:r=-1/p₂。

式(23)是带有常数项的广义Fibonacci序列, 其通项公式为:

η _i=λ ₁[(η ₁-λ ₂η ₀+λ ₇r)-(η ₁-λ ₃η ₀+λ ₈r)]- $\begin{matrix} \frac{r}{p + q - 1} \end{matrix}$ (24)

式中:

λ ₇= $\begin{matrix} \frac{p - 2 - \sqrt[]{p^{2} + 4 q}}{2 (1 - p - q)} \end{matrix}$ , λ ₈= $\begin{matrix} \frac{p - 2 + \sqrt[]{p^{2} + 4 q}}{2 (1 - p - q)} \end{matrix}$

对η _i求和有:

$\begin{matrix} \overset{A - 1}{\sum_{i = 0}} \end{matrix}$ η _i=μ _A-μ ₀=0(25)

由式(22)中μ _A-₁的表达式又有:

η _A-₁= $\begin{matrix} \frac{p_{0}}{1 - p_{0}} \end{matrix}$ η _A-₂- $\begin{matrix} \frac{1}{1 - p_{0}} \end{matrix}$ (26)

联立式(24)(25)(26)可求得η ₀的表达式。又η ₀=μ ₁-μ ₀=μ ₁, μ ₁表示从状态i=B=1出发, 到达吸收态A或0的平均次数, 即给定两级门限的虚警概率后可计算得到噪声单元的平均驻留次数为:

N_n= $\begin{matrix} \frac{k_{1} k_{2} - k_{3} k_{4}}{k_{3} k_{5} - k_{1} k_{6}} \end{matrix}$ (27)

式中:

k₁=λ ₄-λ ₅,

k₂=( $\begin{matrix} λ_{3}^{A - 1} \end{matrix}$ λ ₇- $\begin{matrix} λ_{2}^{A - 1} \end{matrix}$ λ ₈- $\begin{matrix} λ_{3}^{A - 2} \end{matrix}$ λ ₆λ ₇+ $\begin{matrix} λ_{2}^{A - 2} \end{matrix}$ λ ₆λ ₈)r- $\begin{matrix} \frac{r (1 - λ_{6})}{λ_{1} (p + q - 1)} \end{matrix}$ + $\begin{matrix} \frac{λ_{9}}{λ_{1}} \end{matrix}$ ,

k₃= $\begin{matrix} λ_{3}^{A - 1} \end{matrix}$ - $\begin{matrix} λ_{2}^{A - 1} \end{matrix}$ - $\begin{matrix} λ_{3}^{A - 2} \end{matrix}$ λ ₆+ $\begin{matrix} λ_{2}^{A - 2} \end{matrix}$ λ ₆,

k₄=(λ ₄λ ₇-λ ₅λ ₈- $\begin{matrix} \frac{A}{λ_{1} (p + q - 1)} \end{matrix}$ )r,

k₅=λ ₃λ ₅-λ ₂λ ₄,

k₆= $\begin{matrix} λ_{2}^{A - 1} \end{matrix}$ λ ₃-λ ₂ $\begin{matrix} λ_{3}^{A - 1} \end{matrix}$ +λ ₂ $\begin{matrix} λ_{3}^{A - 2} \end{matrix}$ λ ₆- $\begin{matrix} λ_{2}^{A - 2} \end{matrix}$ λ ₃λ ₆,

λ ₉= $\begin{matrix} \frac{1}{1 - p_{0}} \end{matrix}$ 。

同理, 用两级门限的检测概率P_d1、P_d2代替虚警概率P_fa1、P_fa2, 按照上述推导, 即可得到信号单元的平均驻留次数, 与式(27)形式一致。

3.3 检测性能

为了得到第二级门限不同取值对系统虚警概率和系统检测概率的影响, 设置理论仿真条件如下:

(1)取A=4, B=1, T=1 ms, N_nc=1。

(2)取P_FA=10^-⁶, 通过式(8)计算得到P_fa=0.009 934, 将其作为第一级门限对应的虚警概率, 即P_fa1=P_fa。

(3)取P_fa2分别等于10^-³、10^-⁴、10^-⁵、10^-⁶、10^-⁷作为第二级门限对应的虚警概率。

根据式(20)计算得到双门限下的系统虚警概率, 结果如表2所示。

表2 双门限唐检测系统虚警概率 Table 2 System false alarm probability of Tong detection with double thresholds

未增加第二级门限时, 单门限检测算法对应的系统虚警概率为10^-6。增加第二级门限后, 由表2可看出, 双门限检测算法的系统虚警概率有所增加, 但随着第二级门限对应的虚警概率变小(即第二级门限值变大), 双门限检测算法的系统虚警概率随之变小, 且不断逼近单门限检测算法的系统虚警概率10^-6。如在本例中, 当第二级门限所对应的虚警概率小于等于10^-4时, 双门限检测算法的系统虚警概率与单门限检测算法的系统虚警概率已处于同一数量级。

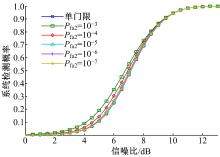
为了分析上述仿真条件下的系统检测概率, 首先分别将P_fa1和不同取值的P_fa2代入式(6)求得对应的门限值, 然后将门限值代入式(7)计算得到单次检测概率P_d1和P_d2, 最后求出不同信噪比下的双门限检测算法系统检测概率, 如图4所示。

	Figure Option View Download New Window
	图4 双门限唐检测系统检测概率Fig.4 System detection probability of Tong detection with double thresholds

从图4可以看出, 不同P_fa2取值下的双门限检测算法系统检测概率在不同信噪比下同单门限检测算法相比均略有提升。随着第二级门限对应的虚警概率变大, 系统检测概率的提升越明显。

当A取其他值时, 双门限检测算法的系统虚警概率和系统检测概率也具有上述特点。即双门限检测算法在检测性能上会增加系统虚警概率和系统检测概率, 但可通过合理设置第二级门限值使其检测性能与单门限检测算法基本相同。

3.4 驻留次数

在相同的理论仿真条件下, 设置不同的第二级门限后, 根据式(27)计算得到的双门限噪声单元平均驻留次数如表3所示。

表3 噪声单元平均驻留次数 Table 3 Average dwell times for noise cells

由表1得到单门限检测算法的噪声单元平均驻留次数为1.0203。与表3的双门限结果对比可以看出, 双门限检测算法对噪声单元的平均驻留次数影响较小, 与单门限时的平均驻留次数基本相等。

不同信噪比下不同第二级门限所对应的信号单元平均驻留次数如图5所示。

	Figure Option View Download New Window
	图5 信号单元平均驻留次数Fig.5 Average dwell times for signal cells

从图5可以看出, 第二级检测门限对应的虚警概率越大, 平均驻留次数越少, 检测速度越快。表4给出了采用双门限检测算法在A取值不同下, 系统虚警概率满足1.2× 10^-6时第二级门限对应的虚警概率大小, 以及此时系统检测概率等于90%时信号单元的平均驻留次数和与单门限结果比较的差值Diff。

由表4可以看出, 双门限检测算法在系统虚警概率从1.0× 10^-6略微提高到1.2× 10^-6的条件下, 能有效减少平均驻留次数, 且A越大次数减少得越多, 从而大大提高了信号单元的检测速度。

表4 双门限唐检测性能 Table 4 Performance of Tong detection with double thresholds

3.5 算法应用

在实际应用中, 双门限唐检测算法的两级门限可通过如下步骤选取:

(1)已知接收机的系统虚警概率要求为P_FA, 通过式(8)计算得到单门限唐检测算法对应的单次检测虚警概率P_fa, 将其作为双门限算法中第一级门限的虚警概率P_fa1, 并通过式(6)计算得到对应的门限值V_t1。

(2)选取n个小于P_fa1的值作为第二级门限的虚警概率估计值 $\begin{matrix} P_{fa 2}^{(n)} \end{matrix}$ , 然后将P_fa1、 $\begin{matrix} P_{fa 2}^{(n)} \end{matrix}$ 代入式(20)求出双门限唐检测算法的系统虚警概率 $\begin{matrix} P_{FA}^{(n)} \end{matrix}$ 。n的大小取决于对虚警概率估计精度的要求。

(3)在使得 $\begin{matrix} P_{FA}^{(n)} \end{matrix}$ 与P_FA处于同一数量级的条件下, 选取 $\begin{matrix} P_{fa 2}^{(n)} \end{matrix}$ 中的最大值作为第二级门限的虚警概率, 即P_fa2=max( $\begin{matrix} P_{fa 2}^{(n)} \end{matrix}$ ), 并通过式(6)求出相应的门限值V_t2。

通过上述方法选取的门限大小可使双门限唐检测算法的系统虚警概率与单门限唐检测算法的系统虚警概率处于同一数量级, 使得算法对接收机系统性能的影响可以忽略。与此同时, 使得系统检测概率的提升最大, 信号单元平均驻留次数的减少也最大, 有效提高了接收机的检测速度。

在各系统可见卫星数为10颗, 三系统联合定位, 驻留时间T=1 ms, 非相干次数N_nc=1, A取12的条件下, 经仿真得出, 采用改进算法对每颗卫星进行捕获检测确认, 共可减少检测确认时间82.161 ms。在针对弱信号的捕获检测中, 需要更大的A, 更长的相干积分时长T和更多的非相干次数N, 此时采用改进算法节省的检测确认时间更为可观。此外, 改进算法仅需额外增加一个比较器, 在实现过程中硬件资源消耗非常少。

4 仿真结果

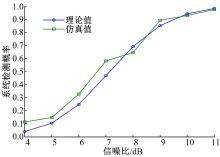
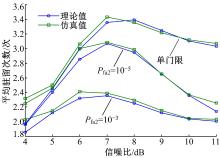
用思博伦GSS9000模拟信号发生器产生不同信噪比的GPS信号, 再用采集器将信号转换为数字中频信号后用于仿真校验。采集器的采样率为16.368 MHz, 数字中频频率为4.092 MHz。仿真条件为A=4, B=1, T=1 ms, N_nc=1, P_FA=10^-⁶, P_fa1=0.009 934。图6为在P_fa2=10^-⁵条件下双门限唐检测算法系统检测概率的理论值与仿真值。图7分别给出了单门限、P_fa2=10^-³、P_fa2=10^-⁵三种情况下的唐检测算法平均驻留次数的理论值与仿真值。

	Figure Option View Download New Window
	图6 系统检测概率仿真结果Fig.6 Simulation result of system detection probability

	Figure Option View Download New Window
	图7 信号单元平均驻留次数仿真结果Fig.7 Simulation result of average dwell times for signal cells

从图6和图7可以看出, 理论与实际仿真结果基本吻合, 从而验证了理论推导分析, 双门限改进唐检测算法确实能有效减少平均驻留次数, 提高检测速度。

5 结束语

针对唐检测算法平均驻留次数过长导致检测速度较慢的问题, 在唐检测算法中引入第二级门限用于比较检测。算法经过了理论推导和性能分析, 并且通过实际仿真校验。结果表明, 双门限唐检测算法在检测性能上会略微增加系统虚警概率和检测概率; 在平均驻留次数上, 噪声单元的平均驻留次数基本不变, 信号单元的平均驻留次数明显减少。因此, 通过给定系统虚警概率选择合适的第二级门限, 使得双门限检测算法可以有效提升检测速度。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zhu Z, Graas F V, Pelgrum W. C/A code cross-correlation at a high doppler offset[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 1826-1838. [本文引用:1]
[2]	刘晓明, 张鹤, 吴皓威, 等. 高动态环境下长码扩频信号快速捕获算法[J]. 电子与信息学报, 2016, 38(6): 1398-1405. Liu Xiao-ming, Zhang He, Wu Hao-wei, et al. Rapid DSSS signal acquisition algorithm under high dynamic environment[J]. Journal of Electronics & Information Technology, 2016, 38(6): 1398-1405. [本文引用:1]
[3]	Zhu C, Fan X. A novel method to extend coherent integration for weak GPS signal acquisition[J]. IEEE Communications Letters, 2015, 19(8): 1343-1346. [本文引用:1]
[4]	Renzo M D, Annoni L A, Graziosi F, et al. A novel class of algorithms for timing acquisition of differential transmitted reference UWB receivers: architecture, performance analysis and system design[J]. IEEE Transactions on Wireless Communications, 2008, 7(6): 2368-2387. [本文引用:1]
[5]	Kaplan E D, Hegarty C H. Understand ing GPS: Principles and Applications[M]. Boston: Artech House, 2006: 223-227. [本文引用:1]
[6]	马琳, 崔嵬, 吴嗣亮. 极低信噪比环境下含近邻约束的改进唐检测判决算法[J]. 系统工程与电子技术, 2011, 33(8): 1745-1749. Ma Lin, Cui Wei, Wu Si-liang. Improved Tong multiple trial algorithm with near neighbor constraint in extremely low SNR condition[J]. Systems Engineering and Electronics, 2011, 33(8): 1745-1749. [本文引用:1]
[7]	马琳, 崔嵬, 田静, 等. 基于马尔可夫链的含有检测次数约束条件的唐检测器[J]. 宇航学报, 2011, 32(8): 1799-1804. Ma Lin, Cui Wei, Tian Jing, et al. Study on Tong detector with number of detection times constraint based on Markov chain[J]. Journal of Astronautics, 2011, 32(8): 1799-1804. [本文引用:1]
[8]	Park H, Lee S. PN code acquisition technique with an adaptive dwell time in DS-SS system[C] ∥ 23rd International Conference on Software, Telecommunications and Computer Networks, Split, Croatia, 2015: 341-345. [本文引用:1]
[9]	谢岗. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009: 286-287. [本文引用:1]
[10]	Proakis J G. 数字通信[M]. 4版. 北京: 电子工业出版社, 2003: 29-31. [本文引用:2]
[11]	姚铮, 崔晓伟, 陆明泉, 等. 应用于GPS接收机的序贯检测器性能分析[J]. 清华大学学报: 自然科学版, 2007, 47(7): 1166-1169. Yao Zheng, Cui Xiao-wei, Lu Ming-quan, et al. Performance analysis of sequential detector for GPS receivers[J]. Journal of Tsinghua University(Science and Technology), 2007, 47(7): 1166-1169. [本文引用:1]
[12]	李思超, 叶甜春, 徐建华. 唐检测器的驻留时间及检测性能分析[J]. 电子测量技术, 2009, 34(3): 53-55. Li Si-chao, Ye Tian-chun, Xu Jian-hua. Analysis on resident time and detection performance of tong detector[J]. Electronic Measurement Technology, 2009, 34(3): 53-55. [本文引用:1]
[13]	朱云龙, 丑武胜, 杨东凯. Tong检测算法性能分析及参数设置[J]. 北京航空航天大学学报, 2015, 41(3): 418-423. Zhu Yun-long, Chou Wu-sheng, Yang Dong-kai. Performance analysis and parameter setting for Tong detection algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3): 418-423. [本文引用:1]

2015

0.0

... 在导航接收机设计中,需要完成信号在时域和频域的二维捕获,并对每个捕获单元的结果进行检测确认^[1,2,3] ...

2016

0.0

. 2016, 38(6):1398-1405 DOI:10.11999/JEIT150860

Rapid DSSS signal acquisition algorithm under high dynamic environment

高动态环境下长码扩频信号快速捕获算法

Liu Xiao-ming , Zhang He , Wu Hao-wei

刘晓明, 张鹤, 吴皓威

① (College of Communication Engineering, Chongqing University, Chongqing 400044, China) ② (Center of Communication and Tracking Telemetering & Command, Chongqing University, Chongqing 400044, China)

For high speed and high dynamic receiver, using long pseudo-noise code, seriously affected by Doppler frequency offset, this paper proposes a double dwell pseudo-noise code acquisition method based on Compressed Code Phase Correlator (CCPC) and FFT. In the first dwell search a rapid and rough compressed search is performed for some neighboring code phase using CCPC, and at the same time the parallel search for Doppler frequency offset using FFT is completed. In the second dwell, all the neighboring code phases acquired in the first dwell are searched accurately using conventional correlator. The theoretical performance analysis model for the proposed method is presented, whose correctness is validated by Monte Carlo simulation. The simulation result shows that the proposed method has obvious advantages compared to Two-Dimensional Compressed Correlator (TDCC) on Mean Acquisition Time (MAT), as well as on the bandwidth and precision of Doppler frequency. Less resources are consumed than other methods based on FFT when using long pseudo-noise code.

针对高速高动态接收机在长伪码周期、大频偏情况下的快速捕获问题，该文提出一种基于码相位压缩相关器与快速傅里叶变换(CCPC-FFT)的双驻留伪码快速捕获方法。在第一驻留阶段，利用码相位压缩相关器对相邻码相位进行快速、粗略的压缩搜索，同时利用FFT算法完成对多普勒频偏的并行捕获；在第二驻留阶段，利用传统的相关积分方法对第一驻留捕获的所有码相位进行逐个精确搜索。给出了系统性能的理论分析模型，并通过蒙特卡洛仿真验证了理论分析的正确性。最后仿真结果表明：新方法在平均捕获时间上比2维压缩相关(TDCC)捕获方法进一步缩短，同时提高了频偏的捕获带宽和精度，且针对长码的捕获比其他基于FFT的方法节省资源。

... 在导航接收机设计中,需要完成信号在时域和频域的二维捕获,并对每个捕获单元的结果进行检测确认^[1,2,3] ...

2015

0.0

... 在导航接收机设计中,需要完成信号在时域和频域的二维捕获,并对每个捕获单元的结果进行检测确认^[1,2,3] ...

2008

0.0

... 由于单次驻留检测的虚警概率过高,无法满足系统要求,需采用多次驻留检测来对捕获结果进行确认^[4] ...

2006

0.0

... 唐检测算法凭借可变的驻留次数、计算量少、结构简单以及在低信噪比下良好的检测性能得到了广泛的应用^[5] ...

2011

0.0

. 2011, 33(8):1745-1749 DOI:doi:10.3969/j.issn.1001-506X.2011.08.13

Improved Tong multiple trial algorithm with near neighbor constraint in extremely low SNR condition

极低信噪比环境下含近邻约束的改进唐检测判决算法

Ma Lin , Cui Wei , Wu Si-liang.

马琳, 崔嵬, 吴嗣亮

For signal acquisition of measurement radar with pseudo-noise code modulated continuous wave in extremely low SNR condition, in order to enhance the sensitivity of Tong algorithm the pseudo-noise code phase differences between two single detections are introduced as near neighbor constraint within a certain range to decide the increase or decrease in value of up/down counter except the threshold condition. The mathematical model of Tong algorithm based on Markov chain is built to analyze the detection performance of improved Tong algorithm with near neighbor constraint. The simulation results show that this architecture can substantially reduce the probability of false alarm while the probability of detection remains almost unchanged, 〗therefore, the detection ability is enhanced compared with the traditional Tong algorithm while the detection speed remains unaffected.

极低信噪比环境下的伪码连续波测量雷达初始粗同步捕获过程中，为了增加唐检测判决算法的灵敏度，除门限条件外，引入前后两次单次检测捕获的伪码相位估计值之差在一定范围内的近邻约束作为上/下行计数器值增减的条件。通过对唐检测判决过程建立马尔可夫链模型，对引入近邻约束的改进唐检测算法的检测性能进行了理论分析与推导。仿真结果表明，将近邻约束引入唐检测判决算法，可以在检测概率几乎不变的情况下，大幅度降低虚警概率，即改进算法明显地增强了对微弱信号的检测能力，且检测速度不受影响。

... 2 理论分析唐检测的数学模型可以采用具有两个吸收态的马尔可夫链来描述^[6,7] ...

2011

0.0

. 2011, 32(8):1799-1804 DOI:doi:10.3873/j.issn.1000-1328.2011.08.022

Study on Tong detector with number of detection times constraint based on Markov chain

基于马尔可夫链的含有检测次数约束条件的唐检测器

Ma Lin , Cui Wei , Tian Jing

马琳, 崔嵬, 田静

Tong detector is a kind of variable dwell detector, and is used to avoid the possibility that the Tong detector get caught in a situation where it satisfies neither k=A nor k=0, the maximum dwell times threshold is set up to help the control and verifying time of direct sequence spread spectrum signal(DSSS signal, henceforth) acquisition. The mathematical model of Tong detector based on Markov chain is built, the first hitting time and sooner-or-later probability of Markov chain are used to analyze the detection performance of Tong detector with detection times constraint. The simulation results show that, if the maximum dwell time threshold is selected reasonably, the detection performance can remain unchanged while the verifying time of DSSS signal acquisition is under effective control.

针对可变驻留次数唐检测器由于驻留次数不定可能导致的单次检测次数已过多，但仍不能满足上/下行计数器值k=A或k=0退出条件的问题，提出一种对单次检测次数设置门限进行约束的方法来避免此种情况发生。将唐检测器建模为齐次马尔可夫链，利用齐次马尔可夫链中的首达时间与迟早概率等定义进行分析，得到含有检测次数约束的唐检测器检测性能公式。仿真结果表明，只要检测次数门限选择合理，可以在检测性能不受影响的情况下通过限制单次检测次数有效控制直接序列扩频信号的捕获验证时间。

... 2 理论分析唐检测的数学模型可以采用具有两个吸收态的马尔可夫链来描述^[6,7] ...

2015

0.0

2009

0.0

... 1 检测统计量接收机天线接收到导航信号后通过射频模块下变频为数字中频信号,再经过解调、解扩、相干积分和清零之后得到I、Q两路信号的表达式如下^[9]: ...

2003

0.0

... 令y=v²,则其概率密度函数为^[10]: ...

2007

0.0

. 2007, 47(7):1166-1169 DOI:doi:10.3321/j.issn:1000-0054.2007.07.021

Performance analysis of sequential detector for GPS receivers

应用于GPS接收机的序贯检测器性能分析

Yao Zheng , Cui Xiao-wei , Lu Ming-quan

姚铮, 崔晓伟, 陆明泉

为了对使用Tong搜索检测器的全球定位系统(GPS)接收机的信号捕获性能进行理论评估,以及在设计中确定该检测器的参数值,推导了该检测器的总虚警概率、总检测概率以及平均驻留时间的计算公式,修正了在此之前研究领域普遍使用的该检测器捕获性能分析公式中的错误,并通过数值验证讨论了该检测器各参数的作用.仿真结果表明:增加Tong搜索检测器内置的计数器初值可以改善捕获性能.在总虚警概率高于0.1%的情况下,降低计数器最大值,同时增加计数器初值可使同等检测概率条件下,平均滞留时间变短.

2009

0.0

. 2009, 34(3):53-55 DOI:doi:10.3969/j.issn.1002-7300.2009.03.016

Analysis on resident time and detection performance of tong detector

唐检测器的驻留时间及检测性能分析

Li Si-chao , Ye Tian-chun , Xu Jian-hua.

李思超, 叶甜春, 徐建华

GPS接收机系统中的搜索检测器对信号的快速可靠捕获有着十分重要的影响.唐检测器计算量适中,在低信噪比下性能优越,受到了广泛关注.本文首先推导了唐检测器平均驻留时间的一般公式,结果显示平均驻留时间与下行计数器值成正比.其次,本文分析和仿真了唐检测器在不同上/下行计数器值下的检测性能,结果表明检测概率随上/下行计数器值的增大而增大.通过适当的设置,在虚警概率为10-6、信噪比为4 dB的条件下,检测概率可达90%.

... 捕获单元仅包含噪声时(噪声单元)的平均驻留次数为^[12]: ...

2015

0.0

. 2015, 41(3):418-423 DOI:doi:10.13700/j.bh.1001-5965.2014.0181

Performance analysis and parameter setting for Tong detection algorithm

Tong检测算法性能分析及参数设置

Zhu Yun-long , Chou Wu-sheng , Yang Dong-kai.

朱云龙, 丑武胜, 杨东凯

Tong detection algorithm is a common used signal detection algorithm. But the overall conclusions about statistical performance and parameter setting of Tong detection algorithm are absent. Aiming at these problems, statistical and recursive analysis methods were used to carry on theoretical analysis about mean value and variance of dwell times in signal search unit in detail, the corresponding expressions were given, a maximum dwell times constraint method was offered according to the 3Sigma principle. The relationships between detection probability, average dwell times of noise search unit and signal search unit, initial value and maximum value of algorithm counter, pre-detection signal to noise ratio were analyzed. Analysis results indicate that the parameters of Tong detection algorithm should be set according to signal strength and search modes, and the influence of parameter setting on detection probability and average dwell times of noise search unit or signal search unit should be balanced.

Tong检测算法是常用的信号检测算法,但在其统计性能以及算法参数设置等方面仍缺少全面的结论.针对这些问题,运用统计和递推分析方法对信号搜索单元滞留次数的均值及方差进行了较为详细的理论分析,给出了相应表达式,根据3西格玛原则,提出了一种最大滞留次数限定方法.分析了检测概率、噪声搜索单元和信号搜索单元平均滞留次数与算法中计数器初值和最大值以及预检测信噪比之间的关系.分析结果表明Tong检测算法参数的设置需依据信号强弱和搜索方式,并折衷考虑对检测概率与噪声搜索单元或信号搜索单元平均滞留次数的影响.

... 捕获单元包含信号时(信号单元)的平均驻留次数为^[13]: ...