非均匀接触对湿式离合器摩擦特性的影响

引用本文

赵二辉, 马彪, 李和言, 杜秋, 吴健鹏, 马成男. 非均匀接触对湿式离合器摩擦特性的影响[J].吉林大学学报（工学版）, 2018,48(3): 661-669
ZHAO Er-hui, MA Biao, LI He-yan, DU Qiu, WU Jian-peng, MA Cheng-nan. Effect of non-uniform contact on friction characteristics of wet clutches[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 661-669 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161386
Permissions

非均匀接触对湿式离合器摩擦特性的影响

赵二辉¹, 马彪^1,², 李和言^1,², 杜秋¹, 吴健鹏¹, 马成男¹

1.北京理工大学机械与车辆学院,北京 100081

2.北京电动车辆协同创新中心,北京 100081

通讯作者：马彪(1964-),男,教授,博士生导师.研究方向:车辆传动理论与技术.E-mail:mabiao@bit.edu.cn

作者简介:赵二辉(1985-),男,博士研究生.研究方向:车辆传动理论与技术.E-mail:zhaoerhuichn@163.com

基金:国家自然科学基金项目(51575042).

摘要

利用接触比率的不同来模拟摩擦副的非均匀接触状态,建立摩擦副润滑摩擦模型,并在湿式离合器综合试验台上进行了相应试验。根据仿真分析和试验结果可知:随着接触比率的减小,摩擦副表面温度显著升高,局部摩擦因数及总摩擦因数明显增大,因此局部摩擦转矩和总摩擦转矩也明显增大。此外,由于接触比率的减小,摩擦副滑摩过程中振动明显增强。所以,由热翘曲所引起的非均匀接触严重劣化了摩擦副的摩擦性能,加速了离合器的损坏。

关键词: 车辆工程; 湿式离合器; 铜基摩擦副; 摩擦特性

中图分类号:U463.2 文献标志码:A 文章编号:1671-5497(2018)03-0661-09

Effect of non-uniform contact on friction characteristics of wet clutches

ZHAO Er-hui¹, MA Biao^1,², LI He-yan^1,², DU Qiu¹, WU Jian-peng¹, MA Cheng-nan¹

1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China

2.Collaborative Innovation Center of Electric Vehicles in Beijing, Beijing 100081, China

Abstract

The non-uniform contact states of friction pairs are simulated by the different contact ratio. A lubrication model of the friction pair is proposed and corresponding tests are conducted on a wet clutch comprehensive test bench. The results simulations and tests show that, as the contact ratio reduces the surface temperature of friction pair increases obviously, and the local friction coefficient and total friction coefficient increase dramatically, so that the local friction torque grows significantly. In addition, the vibration of the output torque becomes more severe when the contact ratio reduces. Therefore, the non-uniform contact after thermal buckling severely deteriorates the friction properties of the friction pairs, and accelerates the failure of the wet clutches.

Keyword: vehicle engineering; wet clutch; Cu-based friction pair; friction characteristics

文章图片

0 引言

铜基湿式多片离合器广泛应用于装甲车辆综合传动转置中。作为换挡和动力传递装置, 湿式离合器在接合过程中可能会因为摩擦副温度的急剧上升和应力场的分布不均而失效。湿式离合器中铜基摩擦副典型的失效形式包括热弹不稳定性或热斑^[1]、热裂纹^[2]和热翘曲^[3]。其中, 热翘曲又被认为是摩擦片失效的主要形式之一。有时候, 摩擦翘曲并不明显且难于在线监测, 但是仍然会导致摩擦副的接触不均匀。而非均匀接触下, 湿式离合器的摩擦特性, 包括摩擦副局部温升、局部摩擦因数与总摩擦因数、局部摩擦转矩与总输出转矩, 将会受到显著影响。

对于湿式离合器的温度场与应力场分布以及摩擦副的非均匀接触等问题, 国内外学者采用理论建模和试验分析的方法进行了研究, 并取得了一定成果。文献[4, 5]通过理论建模和试验对湿式离合器的接合特性进行了分析。离合器结合初始阶段, 摩擦片与钢片处于分离状态, 结合油压较低, 相对转速较高。随着结合油压的快速升高, 摩擦副间隙缩小, 当摩擦副开始接触, 相对转速迅速下降, 摩擦副间温度急剧上升。最终达到锁死油压, 摩擦副完全接合。文献[6, 7]通过仿真和试验的方法研究了湿式离合器接合过程中的温度场和应力场分布。由于摩擦副相对滑动速度沿径向增加, 且内外径润滑及散热条件不同, 导致了温度场和应力场分布的不均匀性。然而, 摩擦副可能因此而失效。文献[8]通过实验的方法研究了湿式离合器的热翘曲问题。文献[9, 10]通过仿真计算研究了湿式离合器的热弹性稳定性问题。文献[11, 12, 13]研究了离合器的摩擦特性及其影响因素。摩擦副容易在急速温升和热应力的作用下发生热失稳和热翘曲, 导致摩擦副的接触不均匀。而非均匀接触又会反作用于摩擦副的摩擦特性, 进一步恶化温度场和应力场的不均匀性, 加速离合器的失效。因此, 彻底研究非均匀接触对湿式离合器摩擦特性的影响对优化控制策略和提高综合传动装置的可靠性具有重要意义。

本文以铜基湿式多片离合器为研究对象, 建立湿式离合器摩擦副非均匀接触润滑摩擦模型, 对四种不同接触比率的摩擦副进行仿真计算, 研究热翘曲所引起的非均匀接触对摩擦副局部温升、局部摩擦因数与总摩擦因数、局部摩擦转矩与总输出转矩的影响。通过人为去除摩擦片上的摩擦材料制作出不同接触比率的摩擦副, 来模拟摩擦副热翘曲后的非均匀接触状态。同时, 为了对比和验证仿真计算结果, 在湿式离合器综合试验台上进行相应试验, 测量不同接触比率下摩擦副的温升、摩擦因数及输出转矩。

1 数学模型及求解过程

1.1 数学模型

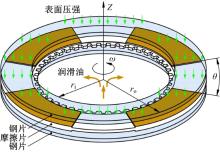
湿式离合器摩擦副非均匀接触润滑摩擦模型如图1所示。在表面压强的作用下钢片与摩擦片接合, 相对转速为 $ω 。$ 摩擦片表面分为接触区和润滑区, 在旋转离心力的作用下润滑油从摩擦副中心甩出, 形成循环润滑回路。

	Figure Option View Download New Window
	图1 湿式离合器摩擦副非均匀接触模型Fig.1 Non-uniform contact friction pair in wet clutch

在润滑区, 流体动压通过求解Reynolds方程获得^[14]:

$\begin{array}{l} \frac{\partial}{\partial x} (\frac{ρ}{12 η} h^{3} \frac{\partial p_{h}}{\partial x}) + \frac{\partial}{\partial y} (\frac{ρ}{12 η} h^{3} \frac{\partial p_{h}}{\partial y}) = \\ \frac{u}{2} \frac{\partial (ρh)}{\partial x} + \frac{\partial (ρh)}{\partial t} (1) \end{array}$

式中: $p_{h}$ 为润滑油动压; u为相对滑动速度; $η$ 为润滑油黏度; $ρ$ 为润滑油密度; h为局部膜厚, 其计算公式为:

$h = h_{0} (t) + δ (x, y, t) (2)$

式中:h₀为初始膜厚; $δ$ 为沟槽深度。

$p_{h}$ 在求解过程中, 需要满足边界条件:

$\{\begin{array}{l} p_{h} (x, y) \geq 0 \\ p_{h} (x, y_{r_{i}}) = p_{h} (x, y_{r_{o}}) = 0 \end{array} (3)$

摩擦副总载荷由润滑油动压和接触压强共同承担, 载荷平衡方程为:

$W = \int \int_{Ω} [p_{h} (x, y, t) + p_{c} (x, y, t)] d x d y (4)$

式中: $Ω$ 为总计算区域; $p_{c}$ 为接触压强, p_c=(W-∬p_hΔ A)/A, Δ A为单元网格面积, A为摩擦副名义接触面积, W为总载荷。

沟槽区, 局部摩擦因数由剪切润滑油膜产生^[15]:

$Δ μ_{h} = \frac{τ_{l}}{p_{h} (x, y)} (5)$

式中: $τ_{l}$ 为润滑油膜剪应力, 本文取2 MPa。

摩擦副接触区, 采用销-盘试验所得局部摩擦因数拟合公式:

$\begin{array}{l} Δ μ_{c} = 23 \exp \{- 2.6 u \{[\ln (T - 273) - 3.2] \cdot \\ {[{(28.3 p_{c})}^{0.4} - 0.87]\}}^{- 1} - 5.16\} + \\ 0.01 \ln (4 u + 1) / \exp [0.005 (T - 273)] + \\ 0.08 \{\exp [0.005 (T - 273) - 1]\} (e^{- 0.2 u} - \\ 1) - 0.005 \ln (28.3 p_{c}) + 0.035 (6) \end{array}$

式中:T为开氏温度。

摩擦副表面局部温升采用点热源积分法求解, 其计算公式为^[16]:

$\begin{array}{l} Δ T (x, y, t) = \int_{0}^{t} \int_{} \int_{Ω_{q}} \frac{q (x', y', t') d x' d y' d t'}{4 ρ_{s} c_{s} {[π α_{s} (t - t')]}^{3 / 2}} \times \\ \exp \{- \frac{{[(x - x') - u (t - t')]}^{2} + {(y - y')}^{2}}{4 α_{s} (t - t')}\} (7) \end{array}$

式中:ρ _s、c_s、α _s分别为摩擦材料的密度、比热容和热扩散率。局部热流密度q可通过下式计算:

$q (x, y) = μ (x, y) p (x, y) Δ Au (x, y) (8)$

式中: $μ (x, y)$ 为局部摩擦因数; $Δ A$ 为单元网格面积; $p (x, y)$ 为局部压强; $u (x, y)$ 为局部相对滑动速度。

摩擦副间热流分配公式为^[17]:

$\{\begin{array}{l} q_{1} (x, y) = - \sqrt{λ_{1} ρ_{1} c_{1}} / (\sqrt{λ_{1} ρ_{1} c_{1}} + \sqrt{λ_{2} ρ_{2} c_{2}}) q (x, y) \\ q_{2} (x, y) = - \sqrt{λ_{2} ρ_{2} c_{2}} / (\sqrt{λ_{1} ρ_{1} c_{1}} + \sqrt{λ_{2} ρ_{2} c_{2}}) q (x, y) \end{array} (9)$

式中:q₁、q₂分别为摩擦片和钢片的局部热流密度; λ ₁、λ ₂分别为摩擦片和钢片的导热系数。

摩擦副总摩擦因数计算公式为:

$μ = \int \int_{Ω} p (x, y) μ (x, y) d x d y / W (10)$

式中: $p (x, y)$ 为局部压强, 包括润滑油动压和接触压强。

摩擦副局部摩擦转矩计算公式为:

$Δ Tor (x, y) = p (x, y) Δ Aμ (x, y) r (11)$

式中:r为局部摩擦半径。

因此, 总输出转矩(包括润滑转矩和接触转矩), 可采用下面积分方法求得:

$Tor = \int \int_{Ω} p (x, y) Δ Aμr d x d y (12)$

1.2 求解过程

本文采用有限差分法求解非均匀接触润滑摩擦模型, 采用松弛迭代法求局部膜厚 $h 、$ 流体动压 $p$ 及局部温升 $t$ 。仿真计算流程如图2所示。无量纲压强 $P$ 和无量纲载荷 $W$ 迭代精度 $ε_{P} = ε_{W} = 10^{- 6}$ ; 无量纲温度 $T$ 迭代精度为 $ε_{T} = 0.5 \times 10^{- 3}$ ; 无量纲膜厚 $H$ 迭代精度为 $ε_{H} = 1 \times 10^{- 6}$ 。合理、有效地划分网格节点密度, 对于仿真计算结果的准确性至关重要。在本文数字模型中, 求解区域被划分为1089个网格节点和960个网格单元。摩擦副钢片由65Mn钢制成, 摩擦片由铜基粉末冶金材料制成, 其材料属性如表1所示。

	Figure Option View Download New Window
	图2 仿真计算流程图Fig.2 Computational flow chart

表1 铜基摩擦副材料特性 Table 1 Material properties of Cu-based friction pair

2 试验方法

为了准确地获得不同速度、温度、压强下的摩擦因数, 本文在摩擦磨损试验机(UMT)上进行了摩擦副小试样销-盘试验。高温湿式旋转销-盘试验模块结构如图3所示。温度为0~150 ℃, 温度控制精度为± 3 ℃。试验过程中, 销子固定于传感器模块中, 摩擦片随载物台一起旋转, 摩擦区域润滑油通过旋转离心力形成循环润滑油路。

	Figure Option View Download New Window
	图3 高温湿式旋转销-盘试验模块Fig.3 Elevated temperature chamber for rotary drives

销-盘试验样品如图4所示。销子由65Mn钢制成, 摩擦片由铜基粉末冶金材料制成。试验前对摩擦副进行充分磨合。

	Figure Option View Download New Window
	图4 小试样销-盘试验样品Fig.4 Test samples of pin and friction disc

试验中工况参数设置如表2所示。本文把摩擦因数看作关于相对滑动速度、温度和平均面压的函数, 根据试验结果, 得到了湿式离合器摩擦副局部摩擦因数拟合公式(见式(6))。

表2 销-盘试验参数设置 Table 2 Parameter settings in pin-on-disc tests

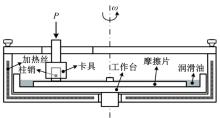
为了比较和验证仿真计算结果, 在湿式离合器综合试验台(见图5)上进行了相应试验。湿式多片离合器输入端由90 kW电机带动, 输出端与转动惯量和制动器连接。试验测试步骤为:①开动电机至目标转速; ②调节控制油压至目标压强, 使摩擦副接合并以目标相对速度转动; ③采集并记录接合初始阶段5 s的转速、控制油压、摩擦副温升及输出转矩; ④减小控制油压分离摩擦副, 停止电机, 结束试验。

	Figure Option View Download New Window
	图5 湿式离合器综合测试试验台Fig.5 Comprehensive test bench of wet multi-disc clutch

试验过程中, 采用单摩擦片与双钢片组成的双摩擦副结构, 摩擦片与电机一起旋转, 钢片由制动器制动, 润滑油在旋转离心力的作用下从中心轴孔甩出, 形成润滑油路。试验中所采用的摩擦片和钢片结构参数如表3所示。

表3 铜基摩擦副结构参数 Table 3 Geometric parameters of Cu-based friction pair

参数	摩擦片	钢片
外径 $r_{o}$ /mm	124	124
内径 $r_{i}$ /mm	86	86
厚度 $H$ /mm	4.2	4

表3 铜基摩擦副结构参数 Table 3 Geometric parameters of Cu-based friction pair

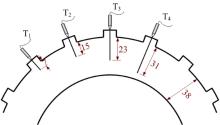
本文采用在钢片内部布置铠装热电偶的方式进行在线测温, 如图6所示。打孔直径为1 mm, 4组传感器T₁、T₂、T₃和T₄布置深度分别为7、15、23和31 mm。传感器测温点距钢片表面距离为1 mm。

	Figure Option View Download New Window
	图6 测温传感器布置图Fig.6 Arrangement of thermocouples in steel disc

3 结果及分析

为了研究非均匀接触下铜基湿式多片离合器的摩擦特性, 本文在仿真计算和试验中采用4种不同接触比率的摩擦副 $CR = 0.2 、 CR = 0.4 、 CR = 0.6 和 CR = 0.8,$ 主要分析摩擦副非均匀接触对表面温升、局部摩擦因数和总摩擦因数、局部摩擦转矩和总输出转矩的影响。仿真计算和台架试验参数设置如下所示:转速为500 r/min; 平均面压为0.7 MPa; 接触比率分别为0.2, 0.4, 0.6和0.8。

试验后, 不同接触比率的摩擦片表面状态如图7所示。由图可以看出:所有摩擦片外径位置都有明显的高温烧蚀痕迹, 且根据烧蚀痕迹颜色的深度可以判断出, 随着接触比率的减小摩擦副表面温升增大, 且外径处局部温升高于内径处。

	Figure Option View Download New Window
	图7 试验后不同接触比率铜基摩擦片Fig.7 Friction plates with different contact ratio after test

3.1 对摩擦副温升的影响

当相对滑摩时长t=5 s时, 不同接触比率下摩擦片表面温升仿真计算结果如图8所示。随着摩擦副接触比率的减小, 在很小的接触面积上形成很大的集中载荷, 使得表面温升显著增大。当接触比率CR=0.8时, 摩擦片最大表面温度约为135 ℃。然而, 随着摩擦副接触比率减小到CR=0.2, 摩擦片最大表面温度增大到约310 ℃。另外, 由于摩擦副相对滑动速度沿径向增大, 因此, 从摩擦片表面温升分布图可以看出, 外径处局部温升高于内径处。但最外径处散热条件良好, 所以, 摩擦副最大局部温升位于最外径靠里位置。

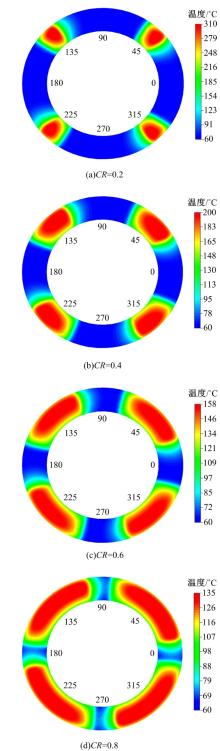	Figure Option View Download New Window
	图8 不同接触比率下摩擦片表面温升仿真计算结果Fig.8 Surface temperature rise of friction plates with different contact ratio

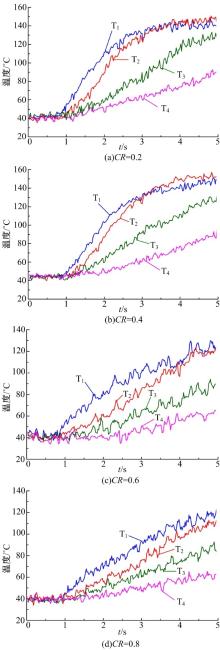
不同接触比率下摩擦副温升试验测试结果如图9所示。测温的初始阶段, 在控制油压的作用下, 摩擦副逐渐接合并以稳定的相对转速运转。当接触比率CR=0.8时, 钢片表面最大温升约为120 ℃。随着摩擦副接触比率减小到0.2, 钢片表面最大温升增加到约150 ℃。对比仿真计算结果可以发现:当接触比例较大时, 仿真计算结果与试验结果吻合较好; 当接触比例变小时, 局部高温面积也随之变小, 并且, 由于润滑油沟槽变宽, 由离心力作用而甩出的润滑油量较多, 摩擦副润滑散热效果更好, 所以钢片中温升并不是特别明显。另外, 当摩擦副接触比率为0.2和0.4时, 传感器T₂处的温度最终超过传感器T₁处的温度, 即最高温度出现在摩擦副外径靠里位置。因此, 摩擦副表面温升仿真计算结果与试验测试结果相符。

	Figure Option View Download New Window
	图9 不同接触比率下摩擦副温升试验测试结果Fig.9 Test results of surface temperature rise on steel discs with different contact ratio

3.2 对摩擦副摩擦因数的影响

摩擦副局部摩擦因数与局部温度、速度和压力有关。图10给出了当相对滑摩时长t=5 s时, 不同接触比率下摩擦副局部摩擦因数仿真计算结果。随着局部温度的升高, 局部润滑油黏度快速下降, 局部流体动压作用减弱, 导致微凸峰接触数量增多, 所以局部摩擦因数显著增大。当接触比率为0.8时, 摩擦副最大表面温度约为135 ℃, 此时最大局部摩擦因数约为0.069。当接触比率减小到0.2时, 最大表面温度增加到约310 ℃, 因此摩擦副最大局部摩擦因数增大到约0.114。从局部摩擦因数分布图可以看出:最大局部摩擦因数位于摩擦副中径位置附近。

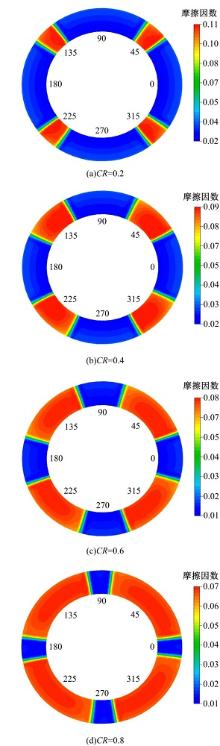	Figure Option View Download New Window
	图10 不同接触比率下摩擦副局部摩擦因数仿真计算结果Fig.10 Local friction coefficient of Cu-based friction pairs with different contact ratio

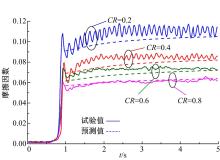
摩擦副总摩擦因数仿真计算与试验测试结果如图11所示。

	Figure Option View Download New Window
	图11 摩擦副总摩擦因数仿真计算与试验测试结果Fig.11 Calculation and test results of total friction coefficient

由于摩擦副间隙消除需要大约1 s, 所以仿真计算从1 s处开始。可以看出, 随着摩擦副接触比率从0.8减小到0.2, 局部摩擦因数显著增大, 因此, 总摩擦因数也明显增大, 最大总摩擦因数从约0.064增大到约0.105。在摩擦副接合的初始阶段, 摩擦副温度快速升高, 导致摩擦因数也快速增大, 随着温升速变的变缓, 摩擦因数的增大速度也随之变缓。另外, 从试验测试结果可以看出:随着接触比率的减小, 摩擦副滑摩过程中振动明显加强, 当接触比率减小到0.2时, 摩擦信号有强烈振动。对比试验测试结果与仿真计算结果可以看出, 在接合的初始阶段, 摩擦副表面实际温升速度大于仿真计算温升速度, 所以摩擦因数实际的增大速度大于仿真计算值, 而随着滑摩时间的增长, 摩擦副表面温度逐渐趋于稳定, 因此摩擦因数试验测试结果与仿真计算值逐渐趋于一致。

3.3 对摩擦副摩擦转矩的影响

图12给出了当t=5 s时, 不同接触比率下摩擦副局部摩擦转矩仿真计算结果。摩擦副局部摩擦转矩与局部摩擦力和摩擦半径有关, 直接受局部摩擦因数的影响, 因此, 随着接触比率的减小, 局部摩擦因数显著增大, 局部摩擦转矩也显著增大。当接触比率CR=0.8时, 最大局部摩擦因数约为0.069, 最大局部摩擦转矩约为0.147 N· m; 当接触比率CR=0.2时, 最大局部摩擦因数约为0.114, 因此最大局部摩擦转矩增大至约0.956 N· m。最大局部摩擦转矩位于摩擦副最外径位置。

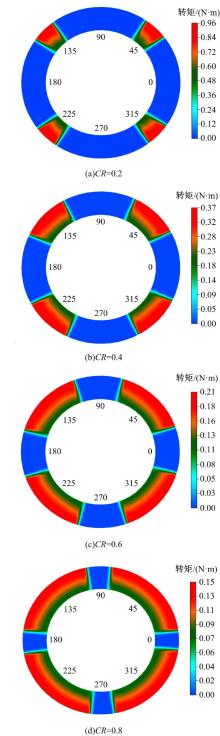	Figure Option View Download New Window
	图12 不同接触比率下摩擦副局部摩擦转矩仿真计算结果Fig.12 Local friction torque of Cu-based friction pairs with different contact ratio

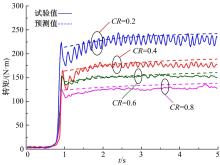
摩擦副总摩擦转矩仿真计算和试验测试结果如图13所示。同样由于摩擦副间隙消除需要大约1 s, 所以仿真计算从1 s处开始。摩擦副总摩擦转矩由局部摩擦转矩积分求得。从图13可以看出:随着接触比率的减小, 局部转矩显著增大, 因此总摩擦转矩也明显增大。随着接触比率从0.8减小到0.2, 摩擦副最大总摩擦转矩从约140 N· m增大到约242 N· m。在摩擦副接合的初始阶段, 由于温升的影响, 摩擦因数快速增大, 因此摩擦转矩也快速增大, 随着温升速度的变缓, 摩擦转矩的增速也随之变缓。同样, 从试验测试结果可以看出:随着接触比率的减小, 摩擦副在滑摩过程中的振动明显增强。对比试验测试结果与仿真计算结果可以看出:在接合的初始阶段, 摩擦副表面实际温升速度大于仿真计算温升速度, 所以摩擦转矩实际的增大速度大于仿真计算结果, 而随着滑摩时间的增长, 摩擦副表面温度逐渐趋于稳定, 因此摩擦转矩试验测试结果与仿真计算值逐渐趋于一致。

	Figure Option View Download New Window
	图13 摩擦副总摩擦转矩仿真计算和试验测试结果Fig.13 Calculation and test results of total output torque

4 结论

(1)随着接触比率的减小, 摩擦副表面温升显著增大, 外径处局部温升高于内径处。但由于最外径处散热条件较好, 所以摩擦副最大局部温升位于最外径靠里位置。摩擦副接合初始阶段温升较快, 而后逐渐变缓。

(2)摩擦副接触比率对摩擦因数具有显著影响。随着接触比率从0.8减小到0.2, 摩擦副最大局部摩擦因数从约0.069增大到约0.114, 最大总摩擦因数从约0.064增大到约0.105。最大局部摩擦因数位于摩擦副中径附近。

(3)摩擦副摩擦转矩受局部摩擦因数和摩擦半径的影响, 因此, 随着接触比率从0.8减小到0.2, 最大局部摩擦转矩从约0.147 N· m增加到约0.956 N· m, 最大总摩擦转矩从约140 N· m增大到约242N· m。最大局部摩擦转矩位于摩擦副外径位置。

(4)随着摩擦副接触比率的减小, 润滑油沟槽变宽, 摩擦副润滑散热条件变好。但是, 由于接触比率的减小, 摩擦副滑摩过程中振动明显增强。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Zhao J, Ma B, Li H, et al. The effect of lubrication film thickness on thermoelastic instability under fluid lubricating condition[J]. Wear, 2013, 303(1): 146-153. [本文引用:1]
[2]	Anderson A E, Knapp R A. Hot spotting in automotive friction systems[J]. Wear, 1990, 135(2): 319-337. [本文引用:1]
[3]	Kao T K, Richmond J W, Douarre A. Brake disc hot spotting and thermal judder: an experimental and finite element study[J]. International Journal of Vehicle Design, 2000, 23(3/4): 276-296. [本文引用:1]
[4]	张志刚, 周晓军, 沈路, 等. 湿式离合器动态接合特性的仿真与试验[J]. 中国公路学报, 2010, 23(3): 115-120. Zhang Zhi-gang, Zhou Xiao-jun, Shen Lu, et al. Simulation and experiment on dynamic engagement characteristics of wet clutch[J]. China Journal of Highway and Transport, 2010, 23(3): 115-120. [本文引用:1]
[5]	Iqbal S, Al-Bender F, Ompusunggu A P, et al. Modeling and analysis of wet friction clutch engagement dynamics[J]. Mechanical Systems and Signal Processing, 2015, 60: 420-436. [本文引用:1]
[6]	Ingram M, Reddyhoff T, Spikes H A. Thermal behaviour of a slipping wet clutch contact[J]. Tribology Letters, 2011, 41(1): 23-32. [本文引用:1]
[7]	杨勇强, 李小莹, 曹博涛, 等. 湿式摩擦离合器摩擦片的热力耦合分析[J]. 机械传动, 2016, 40(1): 153-156. Yang Yong-qiang, Li Xiao-ying, Cao Bo-tao, et al. Thermo-mechanical coupling analysis of friction plate of wet friction clutch[J]. Journal of Mechanical Transmission, 2016, 40(1): 153-156. [本文引用:1]
[8]	Cenbo X, Biao M, Heyan L, et al. Experimental Study and thermal analysis on the buckling of friction components in multi-disc clutch[J]. Journal of Thermal Stresses, 2015, 38(11): 1323-1343. [本文引用:1]
[9]	Zhao J, Chen Z, Yang H, et al. Finite element analysis of thermal buckling in automotive clutch plates[J]. Journal of Thermal Stresses, 2016, 39(1): 77-89. [本文引用:1]
[10]	赵家昕, 马彪, 李和言, 等. 湿式离合器接合过程中的热弹性稳定性[J]. 吉林大学学报: 工学版, 2015, 45(1): 22-28. Zhao Jia-xin, Ma Biao, Li He-yan, et al. Thermoelastic stability of wet clutches during engaging process[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(1): 22-28. [本文引用:1]
[11]	Li Wen-bin, Huang Jian-feng, Fei Jie, et al. Study on tribological properties as a function of operating conditions for carbon fabric wet clutch[J]. Tribology International, 2016, 94: 428-436. [本文引用:1]
[12]	陈思华, 杨翔宇, 任志鹏. 离合器摩擦片摩擦特性试验研究[J]. 润滑与密封, 2016, 41(5): 113-116. Chen Si-hua, Yang Xiang-yu, Ren Zhi-peng. Experimental research on clutch plate friction characteristics[J]. Lubrication Engineering, 2016, 41(5): 113-116. [本文引用:1]
[13]	Dzierwa A. Influence of surface preparation on surface topography and tribological behaviours[J]. Archives of Civil and Mechanical Engineering, 2017, 17(3): 502-510. [本文引用:1]
[14]	Dowson D. A generalized Reynolds equation for fluid-film lubrication[J]. International Journal of Mechanical Sciences, 1962, 4(2): 159-170. [本文引用:1]
[15]	Wang W, Wang S, Shi F, et al. Simulations and measurements of sliding friction between rough surfaces in point contacts: from EHL to boundary lubrication[J]. Journal of Tribology, 2007, 129(3): 495-501. [本文引用:1]
[16]	Carslaw H S, Jaeger J C. Conduction of Heat in Solids[M]. 2nd ed. Oxford: Clarendon Press, 1959: 266-270. [本文引用:1]
[17]	Xin R C, Tao W Q. Analytical solution for transient heat conduction in two semi-infinite bodies in contact[J]. Journal of Heat Transfer, 1994, 116(1): 224-228. [本文引用:1]

2013

0.0

... 湿式离合器中铜基摩擦副典型的失效形式包括热弹不稳定性或热斑^[1]、热裂纹^[2]和热翘曲^[3] ...

1990

0.0

... 湿式离合器中铜基摩擦副典型的失效形式包括热弹不稳定性或热斑^[1]、热裂纹^[2]和热翘曲^[3] ...

2000

0.0

... 湿式离合器中铜基摩擦副典型的失效形式包括热弹不稳定性或热斑^[1]、热裂纹^[2]和热翘曲^[3] ...

2010

0.0

. 2010, 23(3):115-120

Simulation and experiment on dynamic engagement characteristics of wet clutch

湿式离合器动态接合特性的仿真与试验

Zhang Zhi-gang , Zhou Xiao-jun , Shen Lu

张志刚, 周晓军, 沈路

2015

0.0

2011

0.0

2016

0.0

. 2016, 40(1):153-156

Thermo-mechanical coupling analysis of friction plate of wet friction clutch

湿式摩擦离合器摩擦片的热力耦合分析

Yang Yong-qiang , Li Xiao-ying , Cao Bo-tao

杨勇强, 李小莹, 曹博涛

摘　要：在湿式摩擦离合器动力学研究的基础上,采用摩擦功率法对离合器接合过程的热流密度进行了计算。并讨论了摩擦片的对流换热问题,运用有限元技术建立摩擦片模型,对其温度场和应力场耦合情况进行了分析。研究结果表明,摩擦片径向温度随着半径逐渐增大,厚度方向温度升高主要位于摩擦片表面区域。摩擦片外圈区域出现周向拉应力,内圈区域为周向压应力;而摩擦表面出现径向压应力,摩擦片内部出现径向拉应力。该结论为摩擦离合器热失效分析提供了一定的理论基础。

2015

0.0

... 文献[8]通过实验的方法研究了湿式离合器的热翘曲问题 ...

2016

0.0

2015

0.0

. 2015, 45(1):22-28 DOI:doi:10.13229/j.cnki.jdxbgxb201501004

Thermoelastic stability of wet clutches during engaging process

湿式离合器接合过程中的热弹性稳定性

Zhao Jia-xin , Ma Biao , Li He-yan

赵家昕, 马彪, 李和言

On the basis of Thermoelastic Instability (TEI) theory, a theoretical model is proposed to investigate the local hot zones and influence factors of wet clutches during engaging process. The effects of the surface roughness and the mixed lubrication on the temperature and pressure of the friction pair are considered. Under mixed lubrication, the ratios of the lubrication area to the contact area and the fluid shear velocity induced heat flux to the frictional heat flux are calculated. A plasmon resonance analyzer is used to investigate the variation of the surface roughness in different stages. The results show that strong inhomogenous temperature field, hot zones and cold zones appear when the clutch engaging speed exceeds the threshold. The material properties, such as thermal conductivity and elasticity, and structural properties, such as the thickness of the matting disk, significantly influence the stability of the system.

针对湿式离合器接合过程中的局部高温区及影响因素，利用热弹性不稳定性理论(TEI)进行了理论建模与分析。模型中考虑了材料表面粗糙度和混合润滑对摩擦副温度和压力的影响，分析了混合润滑状态下润滑区域与接触区域的比例以及油膜剪切热量与摩擦热量的比例。为了准确测量材料表面粗糙度，设计台架试验，利用表面形貌仪测试了对偶片表面形貌，分析了粗糙度在离合器不同使用阶段的变化规律。结果表明，当离合器接合转速超过临界值时，温度场分布出现明显的波动，高、低温区间隔分布。同时，指出了离合器摩擦材料参数(导热性、弹性)与结构参数(对偶片厚度)对稳定性的影响。

2016

0.0

... 文献[11,12,13]研究了离合器的摩擦特性及其影响因素 ...

2016

0.0

. 2016, 41(5):113-116 DOI:doi:10.3969/j.issn.0254-0150.2016.05.023

Experimental research on clutch plate friction characteristics

离合器摩擦片摩擦特性试验研究

Chen Si-hua , Yang Xiang-yu , Ren Zhi-peng

陈思华, 杨翔宇, 任志鹏

试验研究某车用离合器摩擦片摩擦因数与转速、压力间的关系,通过排除磨损量和温度对摩擦实验结果的影响,得到该摩擦片在不同滑磨速度和压力下的摩擦因数值,发现摩擦因数会随滑磨速度和正压力的增大而减小.对实验数据进行方差分析,结果证明实验结论可靠,并表明转速和压力对摩擦因数的影响相对独立,没有明显交互作用.利用回归分析得到该摩擦片的摩擦因数关于滑磨速度和压强的近似表达式以及摩擦因数变化情况的拟合曲面.通过对比拟合曲面和实验测量值,以及MATLAB分析结果,证明摩擦因数与压力和滑磨速度间的关系可以近似用二元二次方程表示.

... 文献[11,12,13]研究了离合器的摩擦特性及其影响因素 ...

2017

0.0

... 文献[11,12,13]研究了离合器的摩擦特性及其影响因素 ...

1962

0.0

... 在润滑区,流体动压通过求解Reynolds方程获得^[14]: ...

2007

0.0

... 沟槽区,局部摩擦因数由剪切润滑油膜产生^[15]: ...

1959

0.0

... 摩擦副表面局部温升采用点热源积分法求解,其计算公式为^[16]: ...

1994

0.0

... 摩擦副间热流分配公式为^[17]: ...