本文所采用的试验土样为哈尔滨某基坑开挖土体, 土样为淡黄色土体, 具有一定的黏性。对试验土样进行基本的物理力学试验, 根据试验结果结合公路土工试验规程^[11]中对于土体的分类标准, 判定试验土体为低液限粉质粘土, 测得其物理力学参数如下所示:比重G_s=2.65; 最大干密度ρ _d=1.86 g/cm³; 最佳含水量ω _opt=11.4%; 液限ω _L=33.3%; 塑限ω _P=24.0%; 塑性指数I_P=9.3%。

试验中采用的纤维为工程中常用的聚丙烯纤维, 其物理力学参数如下所示:密度为0.96 g/cm³; 抗拉强度为500 MPa; 弹性模量为3850 MPa; 延伸率为10%~28%; 直径为18~48 μ m; 熔点为165 ℃。试验材料如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 试验材料图Fig.1 Test materials

将土体试样风干碾碎并过2 mm的土壤筛。根据击实试验所得到的最佳含水率进行计算称取一定质量的水加入土中, 将试验土样闷料24 h, 使得水分均匀散布在土体内部。运用水泥砂浆搅拌机将纤维与土体进行充分拌合, 使得纤维尽量均匀地分布于土体当中。无侧限抗压强度试验试件制备采用双向静压压实的方法, 试件是高为8 cm、直径为3.81 cm的圆柱形试件。

无侧限抗压强度试验使用LQ-200S型号的公路工程全自动无级变速路强仪, 对制备得到的试验试件进行无侧限竖向加压, 加压速率为0.1 mm/min, 试验仪器自动采集并保存土样的应力应变曲线, 其应力-应变关系曲线中的峰值即为土体试样的无侧限抗压强度。无侧限抗压试验试件加载图片如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 试件加载图Fig.2 Sample upload

响应面试验设计方法的基本原理是根据少量的试验点建立多元回归方程, 并通过回归方程对较优的试验点或试验取值范围进行预测。相较于全组试验, 响应面试验设计法的试验点数较少; 相较于正交试验, 响应面试验设计方法不仅可以得到最优点值, 同时通过拟合方程还可以对试验点进行预测。

响应面试验方法的基本步骤如下:通过单因素试验确定各影响因素的中心点位, 再通过响应面设计得到回归方程, 并进行方差分析。目前, 常用的响应面设计方法有CCD(Central composite design)法和BBD法^[12]。本文采用BBD法进行响应面设计, 所建立的二次回归方程为:

Y=β0+∑i=1kβixi+∑i=1kβiixii2+∑i=1k-1∑j=i+1kβijxixj+ε(1)

式中: Y为响应值; x为影响变量; β为多项式系数; ε为模型误差; k为变量的水平数。

根据参考文献[13]所得结论, 当纤维掺量为3‰ 时, 聚丙烯纤维土的无侧限抗压强度较大, 因此采用3‰ 作为所对应的试验掺量。采用的纤维长度分别为3、6、9、12 mm, 不同纤维长度下聚丙烯纤维土应力-应变曲线变化趋势如图3(a)所示, 无侧限抗压强度变化趋势如图3(b)所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同长度下纤维土无侧限抗压强度趋势Fig.3 Trend of unconfined compressive strength of fiber soil with different fiber length

由图3可以看出:掺入纤维以后, 土体的应力-应变曲线有一定改变, 在应变较小时, 不同长度的纤维土应力-应变曲线是基本重合的, 纤维土的应力峰值出现时, 应变值较大, 在试件发生破坏以后, 素土的应力-应变曲线出现了斜率较大的下滑段, 纤维土的应力-应变曲线应力下降速率并不明显, 其中纤维长度为6 mm的纤维土应力-应变曲线与纤维长度为12 mm的变化趋势基本一致。当曲线出现峰值以后, 随着轴向应变的增大, 轴向应力的下滑趋势并不明显, 此时土体已经出现破裂面, 但是由于纤维的增强, 土体无侧限抗压强度并未迅速丧失, 说明掺加纤维有助于提高土体的韧性。

当纤维掺量为3‰ 时, 聚丙烯纤维土的无侧限抗压强度随着纤维长度的增长出现先增大后减小的变化趋势, 最大无侧限抗压强度对应的长度为9 mm。这是由于当纤维长度较小时, 单根纤维与土颗粒之间的摩擦面积较小, 处于破坏界面上的纤维容易被拔出, 当纤维长度过大时, 根据相关理论, 纤维在加固土体时具有临界长度, 过长的纤维在加固过程中被拔断, 其临界长度计算公式为:

lc=σfr2τ0(2)

式中; lc为单根纤维加固临界长度; σf为单根纤维的抗拉强度; r为纤维直径; τ0为纤维与土颗粒的界面摩擦力。

根据相关研究, 纤维临界长度约为40~80 mm^[5], 对于实际工程当中掺加的短纤维而言, 通常不会出现纤维拔断情况, 但是纤维的锚固长度太长, 并未充分发挥纤维的优势, 同时考虑纤维在整个土体中均匀分布, 在相同掺量下处于破坏界面上的纤维根数较少, 由此引发加固效应减弱。

根据2.1节中所得试验结果, 采用9 mm作为试验纤维长度, 用纤维掺量分别为1‰ 、2‰ 、3‰ 、4‰ 的聚丙烯纤维制备试件并进行无侧限抗压强度试验, 结果如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
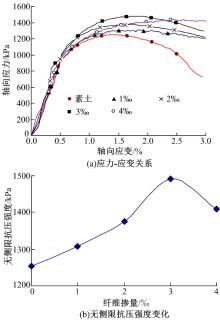	图4 不同掺量下纤维土无侧限抗压强度趋势Fig.4 Trend of unconfined compressive strength of fiber soil with different fiber content

由图4可以看出:随着纤维掺量的增大, 无侧限抗压强度所对应的轴向应变值增大, 纤维的掺入对土体韧性的提高有较大帮助。纤维长度为9 mm的聚丙烯纤维土, 随着纤维掺量的改变同样出现了先增大后减小的趋势, 其中3‰ 为最优掺量, 且对应的无侧限抗压强度值要远高于其余掺量下的纤维土无侧限抗压强度。当纤维掺量较小时, 所掺加的纤维根数较少, 进而引起破坏界面处纤维增强土体的摩擦能力较弱。若纤维掺量过大时, 在搅拌过程中纤维易相互缠绕成团, 在土体中呈现出定向成层分布, 不仅会减弱纤维在土中的三维网状传力体系, 同时多数纤维缠绕在一起形成了剪切面上的受力薄弱区, 由此表现为纤维土的无侧限抗压强度减小。

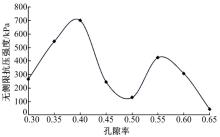
根据以上试验结果, 采用纤维长度为9 mm、纤维掺量为3‰ 作为试件的纤维掺配比。令土体孔隙率分别为0.3~0.65, 并以0.05为间隔点进行试件制备, 得到不同孔隙率下纤维土和素土的无侧限抗压强度, 如图5所示。由于土体本身的无侧限抗压强度会随着孔隙率的增大而减小, 因此采用纤维土和素土在不同孔隙率下的无侧限抗压强度的试验平均值差值(见图6)为研究对象。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同孔隙率下无侧限抗压强度Fig.5 Unconfined compressive strength with different porosity

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同孔隙率下无侧限抗压强度差值Fig.6 Different value of unconfined compressive strength with different porosity

由图5可以看出:纤维土和素土的无侧限抗压强度随着孔隙率的增大呈指数下滑趋势, 纤维土的拟合下滑公式为:

Y=166.07x-2.3996, R2=0.9702(3)

素土的拟合下滑公式为:

Y=228.34x-2.3196, R2=0.9718(4)

根据图6所得结果, 纤维土和素土的无侧限抗压强度差值随着孔隙率的增大出现了双峰趋势, 其中最大差值为0.4, 此时的纤维加筋土体无侧限抗压强度最大。

根据单因素试验所得结论, 设定纤维掺量s(影响因素A)为3‰ 、纤维长度l(影响因素B)为9 mm、孔隙率e(影响因素C)为0.4作为响应面的响应因子中心, 并以无侧限抗压强度作为响应值。其影响因子的编码如表1所示, 根据BBD试验设计原理将试验分成17组, 其中有5组是作为响应因子中心的重复试验, 用于校核试验的误差性, 另外12组为析因试验, 试验点分布在编码正方体的棱点处, 使得试验点整体分布均匀, 用以建立准确的响应面回归方程。试验方案设计及试验结果如表2所示。

表1

Table 1

表1(Table 1)

表1 试验编码 Table 1 Test codes 编码因子 编码水平 -1 0 1 孔隙率 0.3 0.4 0.5 纤维掺量/‰ 1 3 5 纤维长度/mm 6 9 12

表1 试验编码 Table 1 Test codes

表2

Table 2

表2(Table 2)

表2 试验结果 Table 2 Test results 影响因素 响应值 编号 A/‰ B/mm C 无侧限抗压 强度差/kPa 1 3.00 9.00 0.40 669.033 2 3.00 6.00 0.50 465.467 3 3.00 12.00 0.30 257.850 4 5.00 6.00 0.40 577.633 5 1.00 6.00 0.40 283.733 6 5.00 9.00 0.50 485.967 7 5.00 12.00 0.40 306.635 8 3.00 12.00 0.50 407.967 9 1.00 12.00 0.40 465.133 10 3.00 9.00 0.40 700.533 11 3.00 9.00 0.40 634.633 12 1.00 9.00 0.30 307.750 13 1.00 9.00 0.50 384.967 14 3.00 6.00 0.30 606.350 15 5.00 9.00 0.30 426.050 16 3.00 9.00 0.40 629.133 17 3.00 9.00 0.40 626.533

表2 试验结果 Table 2 Test results

3.2.1 方差分析

通过大型试验设计软件Design Expert8.0对所得的实验数据进行分析, 得到纤维掺量、纤维长度、孔隙比对无侧限抗压强度的二次多项回归方程为:

Y=-2019.71+408.16x1+1493.55x2+7051.93x3-18.85x1x2-21.63x1x3+242.5x2x3-34.61x12-11.69x22-11233.25x32R2=0.9429, C.V.=0.1091(5)

同时, 对试验数据进行方差分析, 结果如表3所示。

表3

Table 3

表3(Table 3)

表3 方差分析 Table 3 Variance analysis 来源 总方差 自由度 均方差 F值 p值 Prob> F 模型 322800 9 35866.02 12.84 0.0014 A 15726.51 1 15726.51 5.63 0.0494 B 30702.42 1 30702.42 10.99 0.0129 C 2677.90 1 2677.90 0.96 0.3602 AB 51166.44 1 51166.44 18.31 0.0037 AC 74.82 1 74.82 0.027 0.8746 BC 21170.25 1 21170.25 7.58 0.0284 AA 80717.81 1 80717.81 28.89 0.0010 BB 46626.86 1 46626.86 16.69 0.0047 CC 53130.91 1 53130.91 19.02 0.0033 残差 19556.97 7 2793.85 - - 失拟项 15438.32 3 5146.11 5.00 0.0771 绝对误差 4118.65 4 1029.66 - - 总离差 342400 16 - - -

表3 方差分析 Table 3 Variance analysis

本模型的R²为0.9429, 说明有94.29%的试验结果可以通过回归模型进行解释, 模型的拟合程度较高。变异系数 C.V.值代表试验整体数据的离散程度, C.V.值越小, 说明数据离散程度越低, 数据的可靠性越好。若 C.V.值大于0.15, 则统计数据可能出现异常, 应重复试验。本次试验中, 无侧限抗压强度的 C.V.值等于0.1091, 试验数据具有一定的离散性, 这是由于纤维在拌合过程中可能未达到完全均匀而导致的, 但试验结果仍在可信的范围内。为了进一步检验试验的准确性, 对试验结果进行残差正态性检验, 结果如图7所示。由图7可知:试验点近似分布于一条直线上, 试验结果呈现正态性分布趋势。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 正态性检验图Fig.7 Normality test

在响应面方差检验中, 用F分布来检验各影响因素及其之间的交互作用对试验模型的影响显著性, 其中概率值P(F> F_α )越小, 说明影响效果越显著。通常在统计分布中, F的下确界点分别为0.01、0.05、0.1, 代表影响因素对于模型的影响显著性为:非常显著、显著、较为显著。由表3可知:该模型P值为0.0014, 说明回归模型是显著的, 根据P值结果, 各单因素对于纤维土无侧限抗压强度的影响显著性从大到小排序为:纤维长度、孔隙比、纤维掺量。其中纤维掺量和纤维长度P值均小于0.05, 影响显著; 孔隙比的P值大于0.1, 影响不显著。纤维掺量与纤维长度二者交互项的P值小于0.01, 说明两者交互作用非常显著; 纤维长度与孔隙比交互项的P值满足:0.01< P< 0.05, 说明二者交互作用显著; 纤维掺量与孔隙比交互项的P值大于0.1, 说明二者交互作用不显著。

3.2.2 双因素交互作用

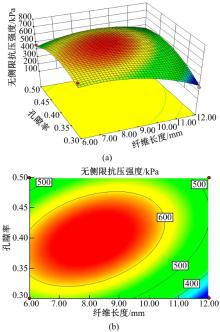
根据表3可知, 模型中纤维掺量与纤维长度、纤维长度与孔隙比均具有显著的交互作用, 说明各影响因素对于纤维土无侧限抗压强度的影响并不是简单的线性关系。因此, 仅对两个影响显著的交互作用进行分析, 二者交互影响的三维图以及所对应的等高线图分别如图8和图9所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 纤维长度与纤维掺量交互作用图Fig.8 Interaction between fiber length and content

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 纤维长度与孔隙率交互作用图Fig.9 Interaction between fiber length and porosity

由图8可知:当纤维长度和纤维掺量较小时, 其无侧限抗压强度的提升并不明显; 当纤维长度较低、纤维掺量较高时, 纤维土无侧限抗压强度有较大程度的提高。通过等高线图可以看出:其等高线呈现出明显的斜向椭圆形, 说明两个影响因素具有明显的交互作用。这是由于纤维掺量与纤维长度均影响纤维加固土体破坏界面的有效加固面积, 在孔隙率相同的情况下, 有效加固面积即为纤维与土颗粒之间的摩擦接触面积。因此, 当纤维掺量较高时, 其加固的交互作用更为明显。但当纤维掺量较高、纤维长度较长时, 纤维容易缠绕成团, 使得加固效果反而减弱。

由图9可知:无侧限抗压强度的三维图呈现出以中心试验点为中心的凸曲面形状, 随着孔隙率以及纤维长度的增加, 在交互作用的影响下, 无侧限抗压强度均出现先增大后减小的趋势。从等高线图可以看出:等高线值呈现出椭圆形, 且沿纤维长度方向的等高线密度较大, 说明在交互作用影响下纤维长度对纤维土无侧限抗压强度的影响更为显著。这是由于无侧限抗压强度的大小从本质上而言可以等效于纤维与土颗粒之间的界面摩擦作用的强弱。摩擦力的大小主要与摩擦接触面积以及土颗粒对纤维的压力有关, 纤维长度越长, 摩擦接触面积越大。孔隙率越低, 土体压实度越大, 使得单位长度的纤维与土颗粒之间的接触面积增大, 同时提高了土颗粒对于纤维的压力作用。但当纤维长度过长、孔隙率较小时, 土颗粒对纤维压力过高, 破坏其原有截面形状, 影响拉应力传递, 同时纤维在土中自身缠绕交织, 在土中成层分布, 影响加固效果。