作者简介:孙正(1989-),男,博士研究生.研究方向:车辆热管理.E-mail:sunz@zju.edu.cn
针对润滑油膜进行计算流体力学(CFD)分析时,空化模型的选取对计算结果有非常显著的影响。本文引入全空化模型,完善了基于CFD的动压润滑数值仿真方法,对比了不同空化现象处理方法对于压力和温度分布计算结果的影响。此外,还比较了不同方法在求解流动传热问题中的适用性和精度差异,进一步验证了CFD方法在求解此类问题时的优势。结果表明:引入全空化模型的CFD方法可将最大压力计算结果精度提升12.1%,压力和温度的整体分布也与试验值更接近;且温度分布计算结果更符合实际;在模拟气穴溃灭过程中,现有全空化模型在计算气穴区域温度分布时仍有改进空间。
In the simulation of hydrodynamics lubrication using CFD based methods, cavitation model has remarkable influence on the simulation results. In this paper, a full-cavitation model is introduced to improve the current CFD based methods. The influences of different cavitation treatment methods on the distributions of pressure and temperature are studied. Further, the applicability and accuracy between Reynolds and CFD based methods are compared. The results show that the accuracy of the maximum pressure is improved up to 12.1%, and the overall pressure distribution is also more close to the experimental data. The temperature distribution with the full-cavitation model is more realistic. However, in modeling the bubble collapsing process, the current full-cavitation model needs to be improved when calculating the temperature distribution in the cavitation area.
径向滑动轴承广泛应用于各类机械传动机构。随着动力装置功率密度的不断提升, 轴承的转速越来越高、承受的载荷越来越大、同时由于结构紧凑性限制等因素, 轴承的冷却条件也相对恶劣, 热效应对轴承性能的影响变得越来越显著[1, 2, 3]。失效现象时有发生。
通过试验与数值仿真相结合的手段, 研究摩擦副在各种工况下的润滑性能, 为轴承设计提供依据, 是解决和避免上述问题的基础。在传统的轴承润滑数值计算中, 多采用基于Reynolds方程的方法[4, 5, 6, 7, 8, 9]。Reynolds方程的推导需对质量、动量守恒方程引入简化假设, 因此丢弃了大量油膜厚度方向的计算信息, 无法精确分析油膜内部的流动传热现象, 无法处理真实的空化现象。在某些情况下, 这些简化可能导致计算结果与实际情况之间存在较大误差。
近年来, 研究人员转而尝试采用计算流体力学(Computational fluid dynamics, CFD)方法求解完整的质量、动量守恒方程, 希望能够克服传统方法的不足[10, 11, 12, 13, 14, 15, 16]。浙江大学Li等[12]计算了轴颈倾斜情况下, 润滑油膜的瞬态流动以及轴承系统整体的动力学特性问题。东南大学张楚等[17]建立了滑动轴承流场数值计算方法, 结果表明, CFD的有效载荷计算结果与试验更加吻合。北京理工大学王康等[18]尝试采用CFD方法对内燃机连杆大头轴承润滑性能进行评估。北京科技大学Li等[19]的研究也表明, Reynolds方法无法准确求解摩擦副表面粗糙度较大的情况。Gertzos等[20]计算了非牛顿流体滑动轴承的润滑性能。重庆大学孟凡明等[21]研究对比了不同CFD求解器对最大油膜压力、承载力等计算结果的影响。通过分析上述文献可以发现, 相比于Reynolds方法, CFD方法可考虑的影响因素更为全面、适用范围更为广泛, 可为动压润滑数值仿真计算提供更为丰富和更为精确的结果, 将成为未来动压润滑数值仿真的趋势。
虽然CFD方法已应用于流体动力润滑过程的研究, 并且为模拟动压润滑中的空化现象提供了必要的基础, 但是在目前多数研究中, 空化现象的处理仍采用简化假设的方法[1, 20, 22, 23, 24, 25, 26, 27], 尚未引入全空化模型[28]。同时, 现有研究对热效应的影响也关注较少, 鲜有探讨不同空化模型对温度分布计算结果的影响。
本文在已有的研究基础上, 引入空化模型, 并考虑热效应的影响, 进一步完善已有的CFD润滑计算方法。并将CFD方法的计算结果与文献[29, 30]中的试验和Reynolds方程仿真结果进行对比, 分析不同仿真方法以及空化模型对径向滑动轴承流动-传热计算结果的影响。
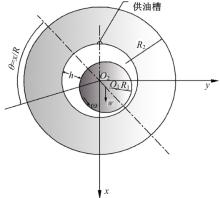
本文以应用广泛的径向滑动轴承为研究对象。轴承模型示意图如图1所示。参考文献[29, 30]对径向滑动轴承进行系统的试验, 获得了压力分布以及温度分布试验数据。因此, 本文将文献[29, 30]中的轴承模型选为本文的仿真对象。轴承系统具体参数如表1所示。载荷施加在轴瓦上, 方向沿图1中
| 表1 轴承参数 Table 1 Journal bearing parameters |
通用形式的连续性方程为:
式中:
动量守恒方程为:
式中:
能量方程为:
式中:
假设液相中存在足够的气核供气泡生成, 且此时液相中随流体运动的气泡与流体间无速度差异, 则可以用Rayleigh-Plesset方程描述:
式中:
采用Singhal模型描述气穴生成和溃灭的过程, 考虑液相和汽相的两相连续性方程为:
式中:
根据Singhal模型:
当
当
式中:
仿真计算中的边界条件设置如下:将图1中的供油槽设置为压力入口, 润滑油入口压力和温度分别如表1所示; 将轴承间隙两侧端面设为压力出口, 表面压力为0; 将轴表面设置为旋转面(Moving wall), 由于轴高速旋转, 假设轴表面温度分度均匀, 温度值与文献[29, 30]中取值相同, 如表1所示; 轴瓦固定不动, 外表面热边界条件设置为第3类边界条件, 取值见表1。
采用ANSYS Fluent 13.0软件作为计算平台, 选用3D-Double Precision-Steady-Pressure Based求解器; 选用Mixture多相流模型; 由于本文算例的
由于润滑油膜各个方向上都包含流动-传热信息。而润滑油膜在油膜厚度方向上尺度很小, 一般为10~100 μ m, 但油膜周向和轴向的尺度都为数十毫米。因此, 仿真计算结果对网格质量非常敏感。在不遗漏各个方向上计算结果的基础上, 同时又能提高计算收敛速度、节省计算资源, 合理的网格划分变得非常重要。本文采用如表2所示的4种网格划分方案, 选取油膜内最大压力和最高温度值进行网格无关性分析。如图2所示, 油膜内最大压力和最高温度计算结果在网格划分方案3以后已趋于稳定。因此, 本文采用表2中网格划分方案3进行后续研究, 即油膜厚度方向布置18层网格; 轴向400层网格; 周向布置360层网格。
| 表2 网格无关性分析 Table 2 Grid independence analysis |
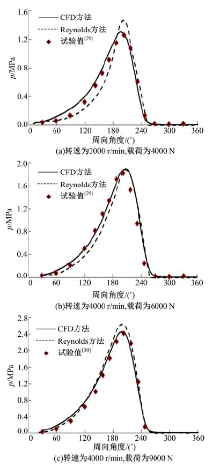
图3给出了采用不同数值仿真方法, 轴瓦中间截面周向压力分布(逆时针方向)计算结果与试验值的对比情况。
图3中, Reynolds方法计算结果和试验数据均来自文献[29, 30]。从图3可以看出:传统Reynolds方法的计算结果, 压力最高点与试验值的误差分别为16.1%、3.6%和8.7%; CFD方法由于采用了黏-温变物性设置, 压力最高点计算结果与试验值误差分别为4.0%、4.1%和1.2%。同时, CFD方法的压力分布计算结果在总体趋势上也更接近试验值。
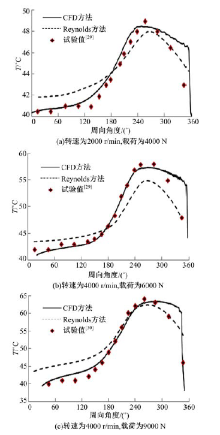
图4为采用不同数值仿真方法, 轴瓦中间截面周向温度分布(逆时针方向)计算结果与试验值的对比情况。
图4中Reynolds方法计算结果和试验数据也均来自文献[29, 30]。从图4可以看出, CFD方法获得的结果无论是在最高温度点还是整体趋势上, 都与试验值更相符, 而Reynolds方法获得的最高温度点计算结果普遍低于试验值。这为上文压力分布的计算结果提供了解释。从表1中的黏-温特性值可以发现, 润滑油黏度对温度变化非常敏感, 而润滑油黏度的空间分布会极大地影响压力分布的计算结果。由于求解时采用CFD方法, 因此获得了更为精确的流动、传热、黏性产热计算结果, 进而获得了更精确的润滑油三维温度分布。与此同时, 通过Fluent求解器中的变物性设置, 将温度分布与黏度分布实时耦合, 进而获得了更精确的压力分布结果。上述分析也在表3中得以体现, CFD方法的压力、温度计算结果均与试验值符合良好。
| 表3 仿真结果与试验值标准差对比 Table 3 Standard deviation of simulation results |
从图4中还可以看出, 采用CFD方法计算温度分布, 在压力建立段(即图1中几何结构收敛段)效果较好。而在几何结构发散段, CFD方法能够模拟出温度分布的骤降, 但过于剧烈, 后段出现较明显的偏差; 传统Reynolds方法的温度分布结果则显得平缓, 两者与试验值都有一定差异。
分析这一现象的原因可能是:后段润滑油膜内的气穴破裂, 压力骤降, 因此下游低温润滑油在背压作用下, 回流进入气穴溃灭形成的真空区域, 与气穴破裂液化后形成的少量液态润滑油混合。混合阶段中, 由于倒流的润滑油在质量上占主要权重且温度偏低, 因此出现了温度的骤降。在CFD仿真中, Singhal空化模型判断油膜内压力一旦低于润滑油的气化压力, 则气穴全部立即开始溃灭, 反映在图上就形成了一个明显的温度拐点。在实际过程中, 气穴的溃灭是相对渐进的过程, 因此温度分布试验值曲线呈缓慢光滑下降。传统方法完全不能模拟气穴生成和溃灭过程, 只是采用Reynolds边界条件或者Half-Sommerfeld边界条件简单地将负压置零, 发散段传热采用简化处理, 因此温度分布过于平缓, 与温度试验结果曲线的趋势存在较大差异。
总体上看, CFD方法获得的温度分布在趋势上与试验值更为接近, 在气穴处理以及发散段温度计算中也更接近物理实际, 与传统方法相比更具优势。但现有的空化模型在判断、模拟气穴溃灭过程这一点上仍有进一步改进的空间。
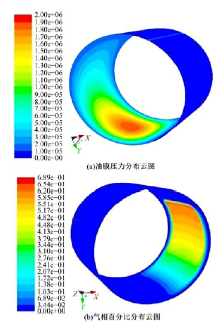
图5为基于CFD方法引入全空化模型后, 润滑油膜内汽相百分比的计算结果云图, 以及产生气穴的区域与油膜压力的对应关系。图5和图6中轴颈旋转方向均为逆时针方向。从图中可看出:在润滑油膜的发散段, 出现了明显的空化区域。传统Reynolds方法, 采用Reynolds边界条件或者Half-Sommerfeld边界条件简单地将负压置零, 并不直接模拟气穴的产生和溃灭过程, 因此无法得到类似图5的计算结果。同样地, 采用CFD方法但不引入全空化模型也无法获得丰富的空化区域三维计算云图。引入全空化模型的CFD方法可为进行径向滑动轴承各项设计参数、结构参数对气穴形成区域的影响规律等后续研究提供数值仿真手段, 并可以获得丰富的两相流计算结果, 相比于Reynolds方法和以往CFD方法的局限, 体现出明显的优势。
在以往文献中[20, 22], 虽然已采用了CFD方法求解径向滑动轴承流动问题, 但仍采用简化方法处理空化现象, 具体做法是利用Fluent UDF中的DEFINE_ON_DEMAND命令对可能产生气穴的区域施加Half-Sommerfeld边界条件。但在文献中只展示了采用这种方法后, 压力分布计算结果与试验值的对比, 并未讨论其对温度分布的影响。
图6为不同空化模型对温度分布的影响, 其中, 轴承转速为2000 r/min, 载荷为4 kN。从图6可以看出, 不同空化现象处理方法对径向滑动轴承几何发散区域的温度分布计算结果有明显影响:①采用Half-Sommerfeld边界, 只对压力计算结果做置零处理, 因此发散区域是理应产生气穴的区域, 在数值计算处理中, 完全由出口和间隙侧面压力边界中的回流填充, 而回流的润滑油温度取决于人为设定值, 图中上方的蓝色区域即反映了这种情况。②采用Singhal模型处理空化, 由于考虑了实际生成气穴的物理过程, 抑制了上述不合理的润滑油回流问题。
因此, 若想要获取精确的径向滑动轴承温度分布计算结果, 需要考虑气穴的影响, 引入完整的空化模型, 仅采用简化的空化现象处理方法所获得的结果与实际情况存在较大差异。
(1)相比于传统方法, 采用CFD方法获得的油膜最高压力点计算结果与试验值更接近; 同时整体压力分布也与试验值更相符。
(2)在CFD方法中引入全空化模型, 可以获得更精确的流动、传热、黏性产热计算结果, 从而获得更精确的润滑油三维温度分布。结合黏-温分布的实时耦合手段, 可使油膜压力分布计算结果更精确。而仅在CFD方法中应用简化空化现象处理方法时, 温度分布计算结果与实际存在较大差异。
(3)CFD方法在求解气穴生成-溃灭、流动传热、黏性产热等流动-传热问题上, 采用的数值处理方法更符合物理实际。尤其是在对空化现象的模拟中, 可以得到传统方法无法获取的丰富仿真结果, 体现出了较明显的优势。不足之处在于, 在油膜结构发散段的气穴溃灭混合和温度计算问题上, 现有空化模型仍有进一步改进的空间。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|